圆弧兜孔圆柱滚子轴承的动态不稳定规律特性研究
2019-03-25刘延斌张占立
刘延斌, 邱 明, 张占立
(1. 河南科技大学 机电工程学院,洛阳 471003; 2. 河南科技大学 机械装备先进制造河南省协同创新中心,洛阳 471003)
圆柱滚子轴承用途广泛,航空发动机中支承转子的主轴承采用的就是圆柱滚子轴承,是发动机的关键部件,其耐久性对飞机的性能和安全起着决定性的作用。这种轴承通常工作在高速轻载的环境下,极易发生滚子打滑、保持架涡动等不稳定现象[1-2],进而引发轴承的磨损、断裂等故障,使轴承发生早期失效,圆柱滚子轴承的滚子打滑和保持架涡动等问题已成为航空发动机主轴承耐久性的主要瓶颈,所以找到圆柱滚子轴承动态不稳定的影响因素及影响规律具有重意义。
Cavallaro等[3]分析了不同径向载荷、不同内外圈转速下滚子打滑速度与Hertz压力之间的关系。Yoshida等[4]在考虑润滑油非牛顿流变特性、温升以及滚子歪斜等因素的情况下,建立了根据轴承结构参数和工况条件预测保持架和滚子打滑的解析模型。Laniado-Jácome等[5]分析了径向游隙、转速和摩擦因数对滚子打滑的影响规律。Selvaraj等[6]分析了转速、径向载荷、润滑油黏度、滚子数及轴承温度对保持架打滑的影响规律。张占立等[7]分析了不同径向载荷下、不同周向位置处滚子自转速度和打滑的变化规律。胡绚等[8]研究了保持架转速和滚子自转速度随径向载荷变化的规律。杨海生等[9]分析了转速、径向载荷及径向游隙对滚子打滑的影响规律。邓四二等[10]分析了引导方式和内外圈旋转方式对轴承打滑的影响。刘红彬等[11]研究了内圈转速、径向载荷和过盈配合产生的压力等因素对滚子打滑的影响。金海善等[12]分析了径向载荷对滚子打滑的影响规律。姚廷强等[13]分析了不同工况下滚子和保持架角速度的变化规律。毛宇泽等[14]分析了轴承径向负游隙对滚子打滑的影响规律。简言之,目前对滚子打滑和保持架涡动的影响因素及规律已经有了大量而深入的研究,这些因素包括载荷、内外圈转速、轴承温度、径向游隙、滑油黏度、滚子数、引导方式、间隙比、滚道形状、滚子结构等,但是关于保持架兜孔型面对滚子打滑和保持架涡动影响规律的研究却鲜见报道。
本文则以具有圆弧保持架兜孔结构的圆柱滚子轴承(以下简称圆弧兜孔圆柱滚子轴承)为对象,建立动力学模型,拟通过数值仿真,对高速轻载工况下滚子打滑和保持架涡动进行分析,初步探讨兜孔的弧面半径、弧面偏置角对滚子打滑和保持架涡动的影响规律。
1 圆弧兜孔圆柱滚子轴承
图1(a)为圆弧兜孔圆柱滚子轴承的三维外观图,保持架采用外圈引导方式。该轴承保持架兜孔的结构和几何参数如图1(b)、1(c)所示,其中参数Ru、Rh分别为兜孔前、后壁弧面的半径;β、α分别为兜孔前、后壁弧面的偏置角;R0=Rn+r0-δ0,Rn为内圈滚道的半径,r0为滚子的标称半径,δ0为预紧时滚子的单侧变形量;σ为滚子与兜孔间隙。设定该轴承工作时,保持架相对外圈按图1(b)所示的方向单向旋转。
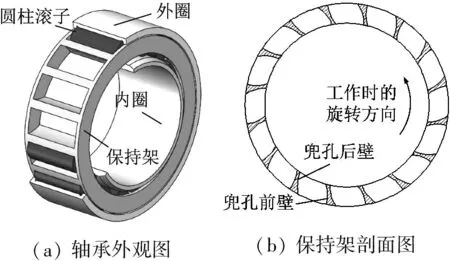
(a) 轴承外观图(b) 保持架剖面图
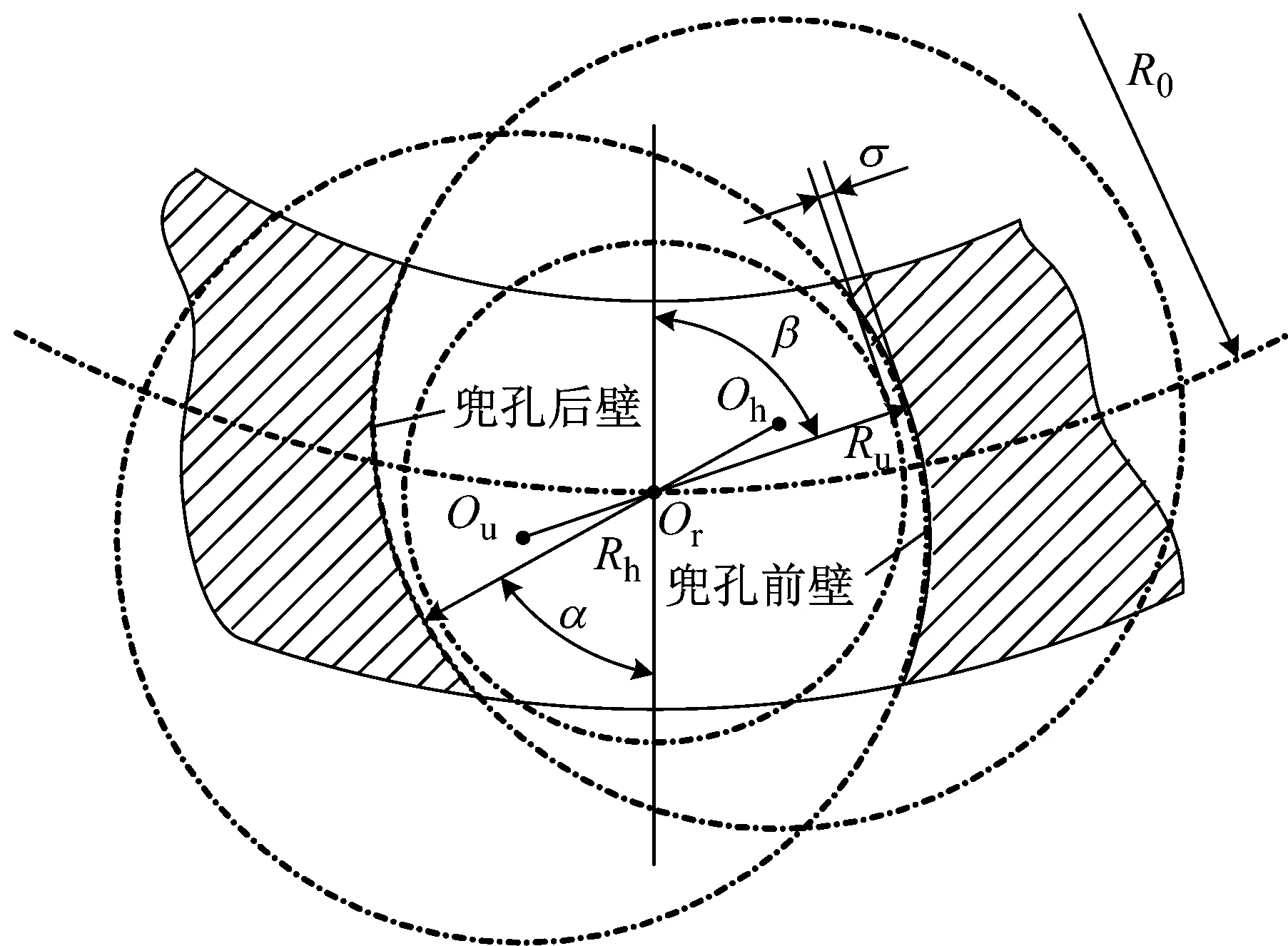
(c) 兜孔结构及参数示意图
2 轴承动力学模型
高速轻载工况下圆柱滚子轴承的动力学机理极为复杂,建立精准的动力学模型难度非常大。本文的主要目的是通过对比分析的方法,初步探讨轴承的圆弧兜孔几何参数对滚子打滑和保持架涡动的影响规律,因此具有些许误差的分析模型不会实质影响对比结果。为此忽略次要因素,只考虑滚子、保持架在轴承径向平面内的主运动,并假定外圈不动、内圈转动,接触副的接触作用力皆采用传统的经验公式来表征,在此基础上建立系统的动力学模型。
2.1 接触副的接触作用力
(1)滚子与内外圈滚道的接触作用力
滚子与内外圈滚道的接触作用属于润滑摩擦作用和Hertz线接触作用,其法向作用力大小可根据Palmgren的线接触负荷变形关系模型[15]及非线性连续碰撞力模型[16]得到
(1)
式中,Er、Et分别为滚子、内外圈的弹性模量;νr、νt分别为滚子、内外圈的泊松比;L为滚子长度;δrt为接触变形量(渗透量);αe为弹性恢复拟合系数。
滚子与内外圈滚道的切向作用力大小为
Trt=μrtNrt
(2)
式中,μrt为摩擦因数[17-18]
Λ为油膜参数
hc为接触区中心油膜厚度(其计算方法详见文献[17]),σr、σt分别为滚子、滚道的表面粗糙度;μbd为边界润滑摩擦因数
μbd=(-0.1+22.28s)exp(-181.46s)+0.1
s为滑滚比;μhd为油润滑时的弹流润滑摩擦因数,可采用如下的经验公式计算[19]
μhd=(λ1+λ2s)exp(-λ3s)+λ4
λ1、λ2、λ3、λ4为试验回归得到的系数,与温度、压力及滚动速度有关(其计算方法详见文献[19])。
(2)滚子与保持架兜孔的接触作用力
设Δ0为接触状态转变的油膜厚度临界值,它由滑油和表面粗糙度等因素综合确定。当滚子与保持架兜孔的最小间隙hrb≥Δ0时,滚子与兜孔间未发生碰撞,仅存在流体动压作用,无Hertz接触作用,此时滚子与兜孔的接触作用可简化为圆柱刚体与平面的流体动压作用,滚子与兜孔流体动压产生的法向作用力大小为
(3)
式中,η0为大气压下润滑油的动力黏度;vr、vb分别为滚子、兜孔壁的切向速度;r为滚子半径;h为接触区的中心油膜厚度
滚子圆柱面与兜孔壁面间的切向作用力(不计入口流体对滚子和兜孔的泵吸作用)大小为
(4)
当hrd<Δ0时,滚子与兜孔间发生碰撞,其相互作用变为润滑摩擦作用和Hertz线接触作用,此时的接触变形量为
δrd=Δ0-hrd
其法向作用力大小变为
(5)
其中系数Krd、Crd参照式(1)的方法计算。
滚子圆柱面与兜孔壁面间的切向作用力大小变为
(6)
其中系数μrd参照式(2)的方法计算。
(3)保持架与外圈引导面的接触作用力
当保持架与外圈引导面的最小间隙hbw≥Δ0时,保持架与外圈引导面间未碰撞,仅存在流体动压作用,而无Hertz接触作用,此时保持架与外圈引导面的作用可等效为短滑动轴承作用[20],如图2(a)所示,当外圈不动时,保持架受到外圈的作用力为
式中,rb为保持架中心Ob在惯性系O-XY中的位置坐标列阵;e=rb为保持架中心Ob相对外圈中心Ow的偏心量;
保持架受到外圈引导面的摩擦阻力矩大小为
式中,U=Rωb,R为保持架上的引导表面半径,ωb为保持架转速;B为引导面宽度;C为半径引导间隙;ε=e/C。
当hbw<Δ0时,保持架与外圈引导面发生碰撞,如图2(b)所示,其相互作用暂等效为润滑摩擦和Hertz线接触的联合作用[21],此时的接触变形量为
δbw=Δ0-hbw
其接触作用力变为
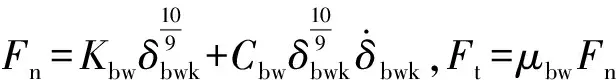
其中系数Kbw、Cbw参考式(1)的方法计算,系数μbw参考式(2)的方法计算。
保持架受到外圈引导面的摩擦阻力矩大小则变为
Mbw=Mf+FtR
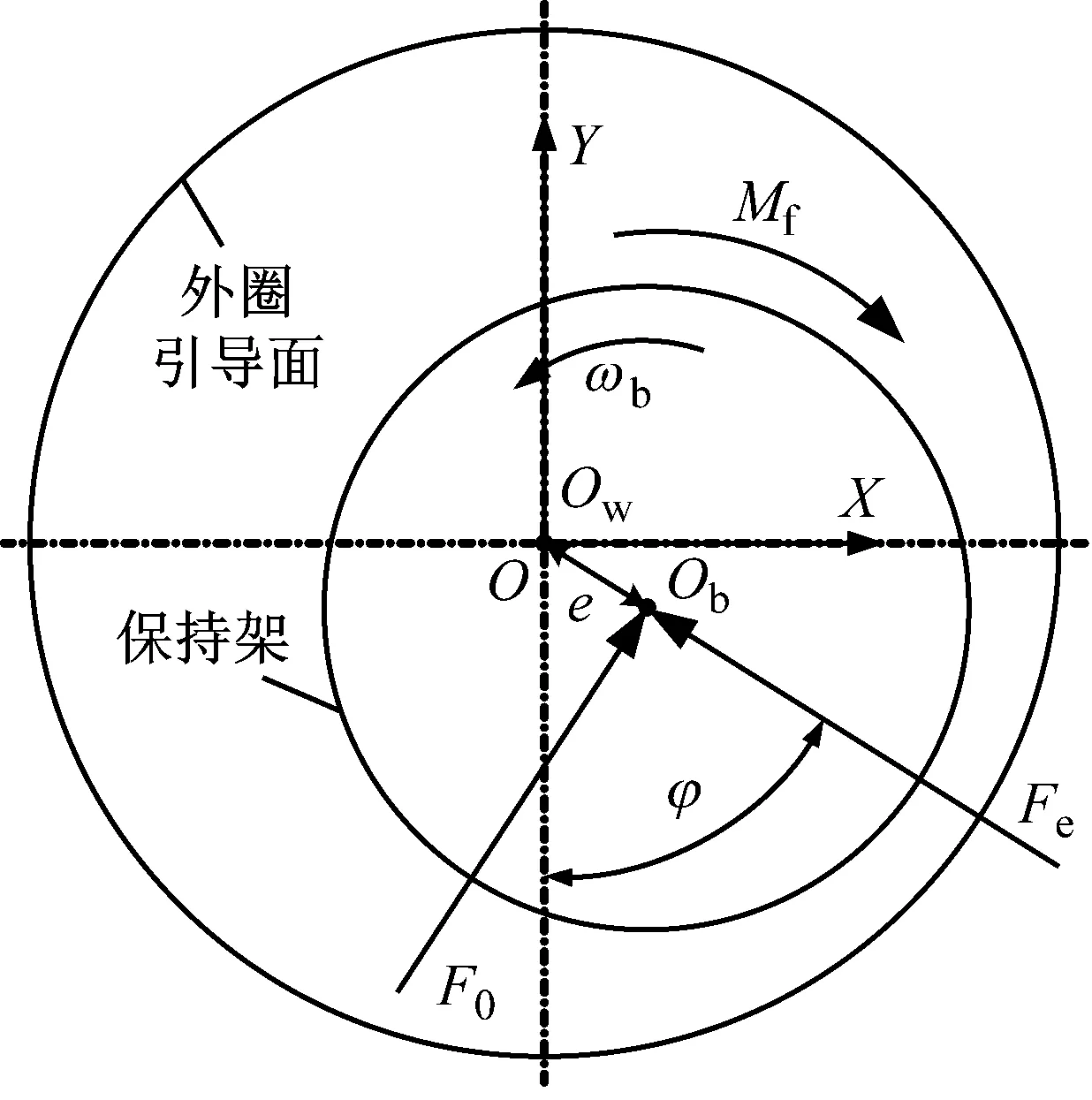
(a) 保持架与外圈引导面未碰撞

(b) 保持架与外圈引导面碰撞
2.2 接触副的接触变形量
如图3,将转子对轴承内圈的径向载荷简化为位移载荷ΔF,On为内圈中心,Ori为第i(i=1,2,…,n)个滚子中心,Ohi为第i个兜孔后壁弧面中心,Oui为第i个兜孔前壁弧面中心,惯性参考系O-XY与外圈固结,其原点O与外圈中心Ow重合。
第i个滚子与兜孔前壁的最小间隙为
hrui=Ru-rri-rui-ri
式中,rri=[xriyri]T
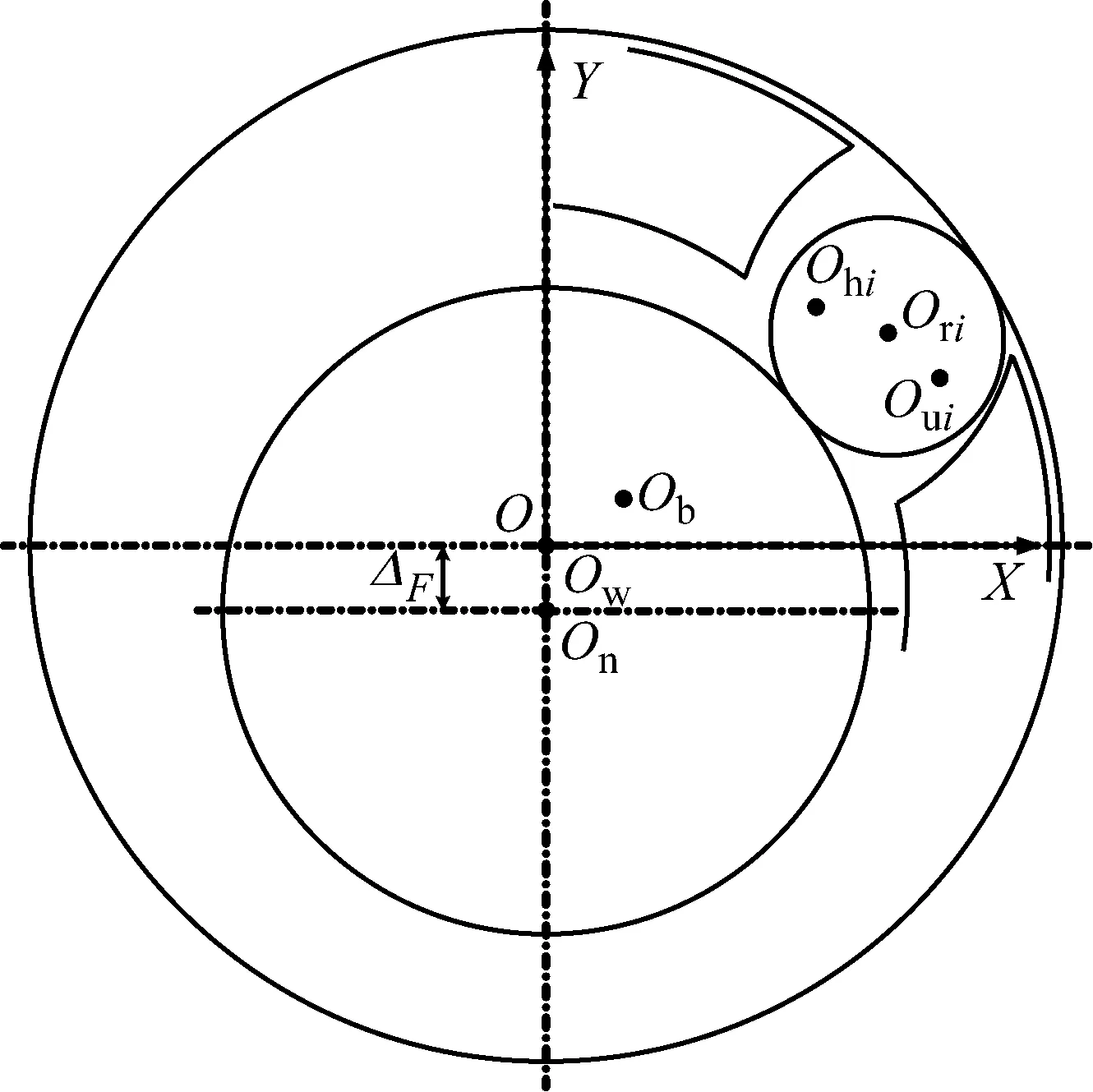
图3 轴承工作状态示意图
Φi=ϑb+θi
ri为第i个滚子的实际半径;xri、yri分别为第i个滚子在惯性系中的X、Y坐标分量;xb、yb分别为保持架中心Ob在惯性系中的X、Y坐标分量;ϑb为保持架相对惯性系的转角;θi为保持架的第i个兜孔相对惯性系X轴的初始方位角。
当hrui<Δ0时,第i个滚子与兜孔前壁则发生碰撞接触变形
δrui=Δ0-hrui
第i个滚子与兜孔后壁的最小间隙为
hrhi=Rh-rri-rhi-ri
式中
当hrhi<Δ0时,第i个滚子与兜孔后壁则发生碰撞接触变形
δrhi=Δ0-hrhi
第i个滚子与内圈滚道的最小间隙为
hnri=rri-rn-ri-Rn
式中,rn=[0 -ΔF]T。
当hnri<0时,第i个滚子与内圈滚道则发生滚压接触变形
δnri=-hnri
第i个滚子与外圈滚道的最小间隙为
hwri=Rn+2r0-2δ0-rri-ri
当hwri<0时,第i个滚子与外圈滚道则发生滚压接触变形
δwri=-hwri
保持架与外圈引导面的最小间隙为
hbw=C-e
当hbw<Δ0时,保持架与外圈引导面发生碰撞接触变形
δbw=Δ0-hbw
2.3 接触副的滑动速度
在第i个滚子与外圈滚道接触副中滚子沿接触点切向的速度为
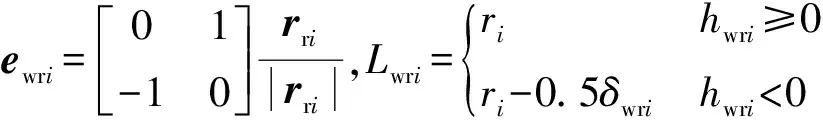
ωri为第i个滚子的绝对角速度。
在第i个滚子与内圈滚道接触副中滚子沿接触点切向的速度为
内圈滚道沿接触点切向的速度为
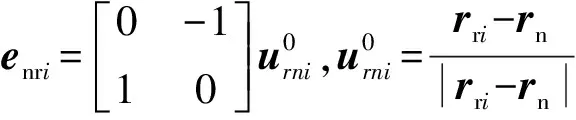
ωn为内圈的转动速度。
在第i个滚子与第i个兜孔前壁接触副中滚子沿接触点切向的速度为
兜孔前壁沿接触点切向的速度为
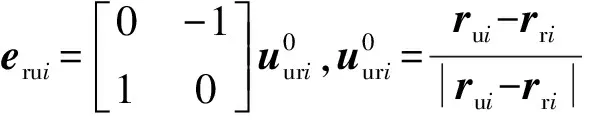
在第i个滚子与兜孔后壁接触副中滚子沿接触点切向的速度为
兜孔后壁沿接触点切向的速度为
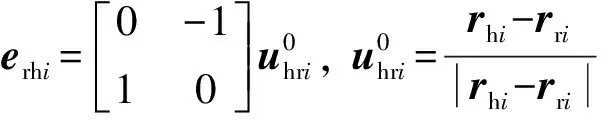
2.4 滚子的动力学方程
第i个滚子的牛顿方程(不计重力)
式中,Nrui、Nrhi分别为第i个滚子与兜孔前、后壁的法向作用力,都按式(3)和(5)进行计算;Trui、Trhi分别为第i个滚子与兜孔前、后壁的切向作用力,都按式(4)和(6)进行计算;Nnri、Nwri分别为第i个滚子与内、外圈滚道的法向作用力,都按式(1)进行计算;Tnri、Twri分别为第i个滚子与内、外圈滚道的切向作用力,都按式(2)进行计算;mri为第i个滚子的质量。
第i个滚子的欧拉方程
式中,Jri为第i个滚子的转动惯量。
2.5 保持架的动力学方程
保持架的牛顿方程(不计重力)
式中,mb为保持架的质量。
保持架的欧拉方程为
式中,Jb为保持架的转动惯量;t(1)、t(2)分别表示矢量t的X、Y轴分量;u(1)、u(2)分别表示矢量u的X、Y轴分量。
3 轴承动态不稳定规律的仿真分析
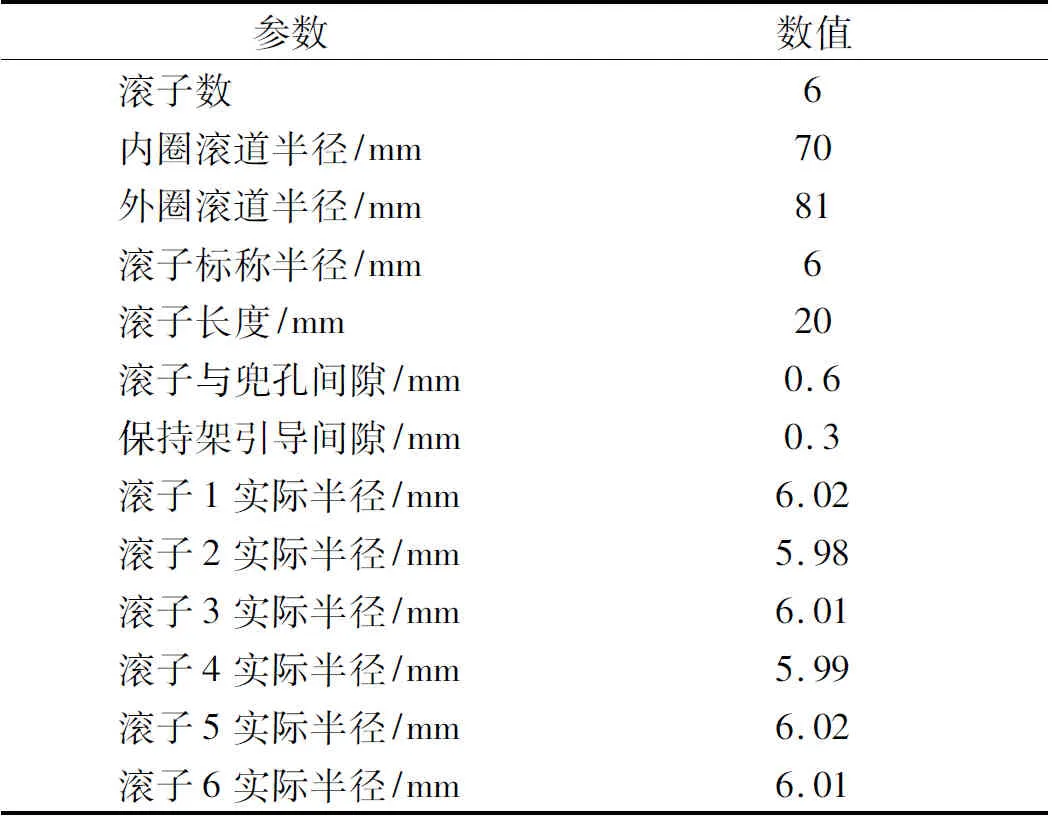
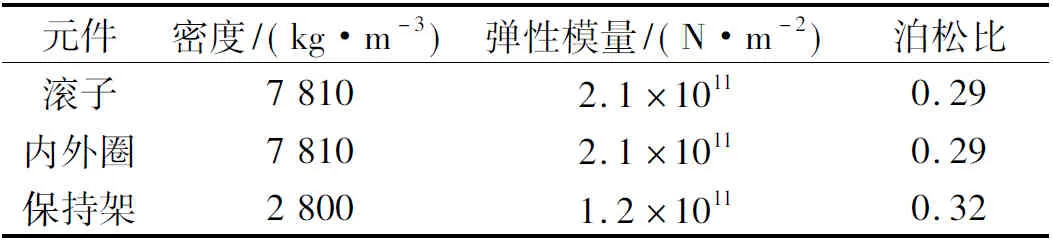
轴承的几何参数、材料特性参数以及工况条件参数如表1、2、3所示,并假设供油充分,环境温度为常温。
滚子打滑时保持架的转速会降低,因此滚子打滑通常以保持架平均打滑率来表征
式中:N为采样数据个数;sb(k)为保持架瞬时打滑率的第k个采样值
ωbt(k)、ωb(k)分别为保持架理论转速和实际转速的第k个采样值。

对于保持架的稳定性,可以根据其质心运动状态来判定,当保持架质心轨迹为一点时,保持架的稳定性最好;当保持架质心出现涡动时,则通常根据质心的涡动轨迹及涡动速度变化来判断保持架的稳定性,具体而言,当保持架质心涡动轨迹近乎圆形且涡动速度变化不大时说明保持架的质心处于稳定的涡动状态,当质心涡动轨迹为多边形甚至紊乱的轨迹且质心涡动速度变化很大时说明保持架的质心处于不稳定的涡动状态。关于质心涡动速度变化程度,可以通过计算质心的涡动速度偏差比来判定[21],其计算方法如下
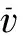
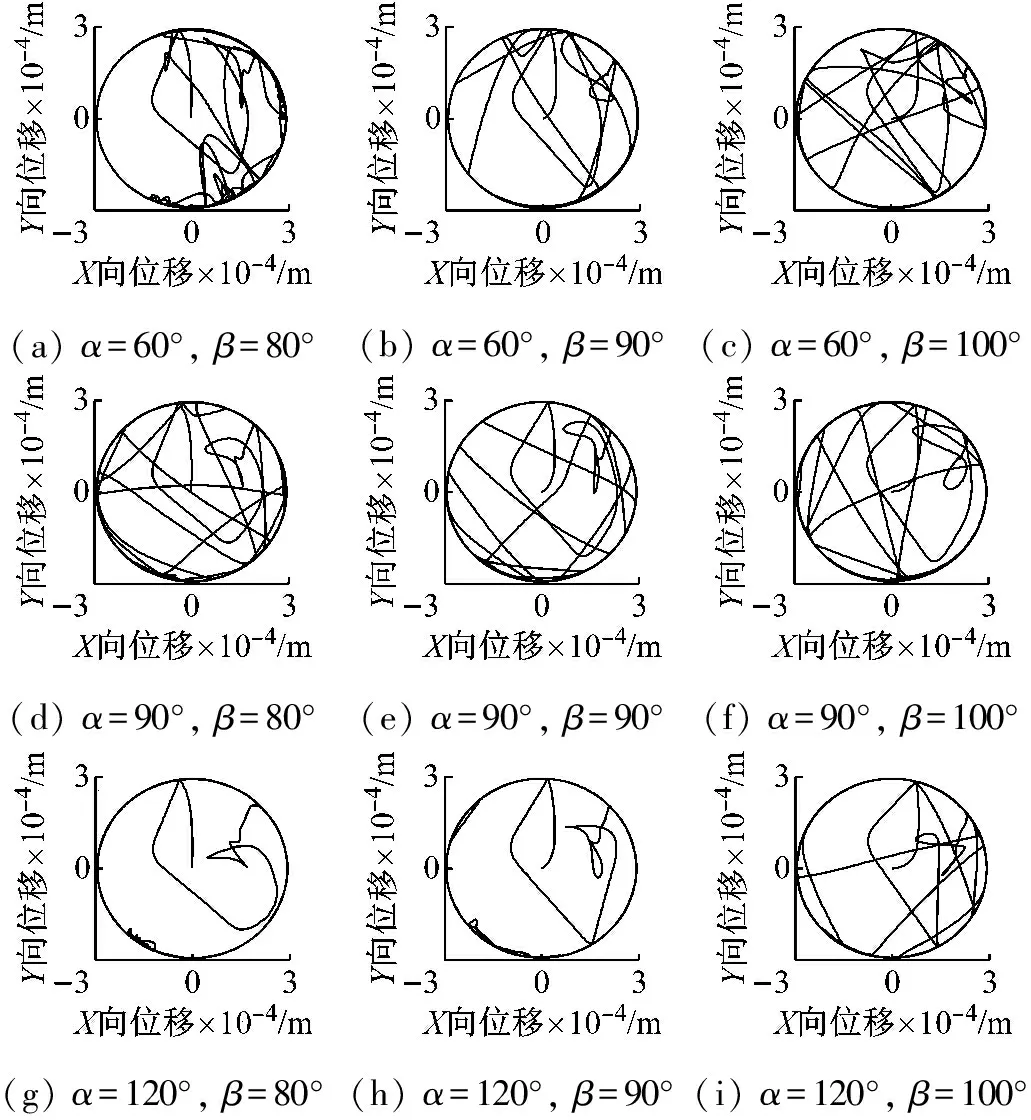
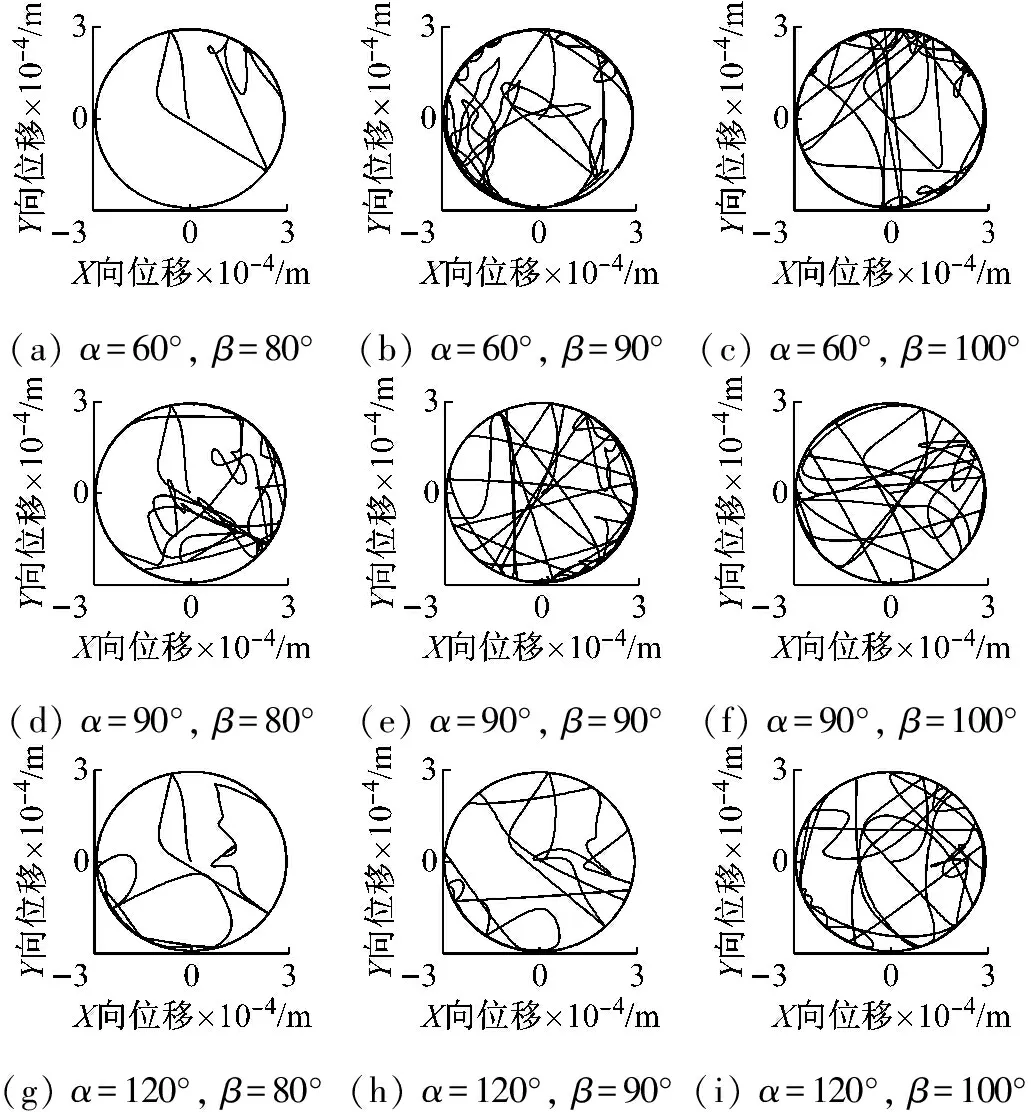
在不同的兜孔弧面半径、不同的弧面偏置角(如图4所示)下,对圆弧兜孔轴承进行动态稳定性仿真,其中表4、5为保持架的平均打滑率,表6、7为保持架质心的涡动速度偏差比,图5、6为保持架质心的涡动轨迹。
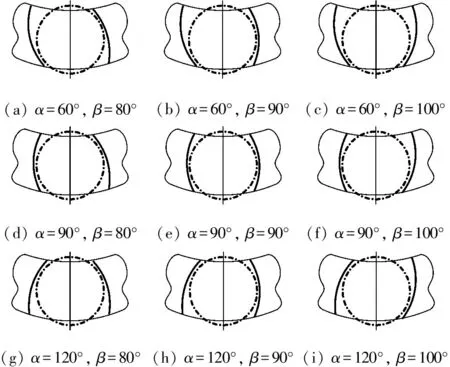
(a) α=60°, β=80°(b) α=60°, β=90°(c) α=60°, β=100°(d) α=90°, β=80°(e) α=90°, β=90°(f) α=90°, β=100°(g) α=120°, β=80°(h) α=120°, β=90°(i) α=120°, β=100°
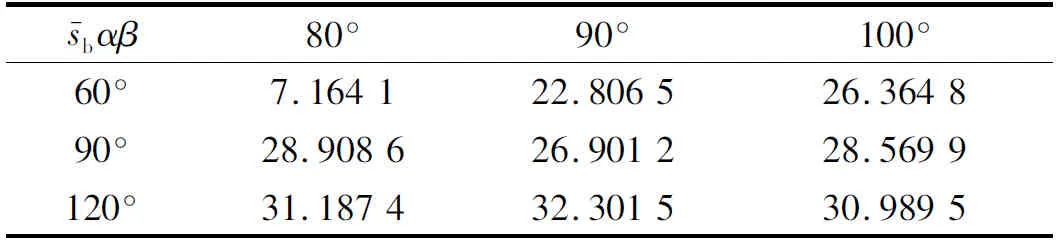
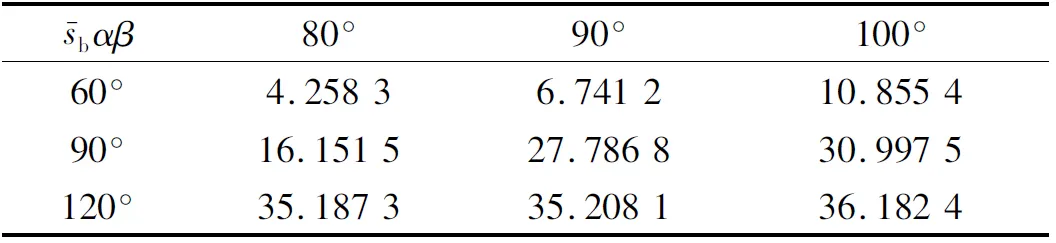
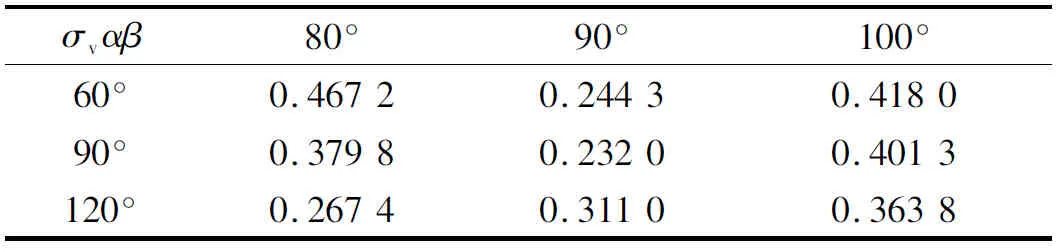
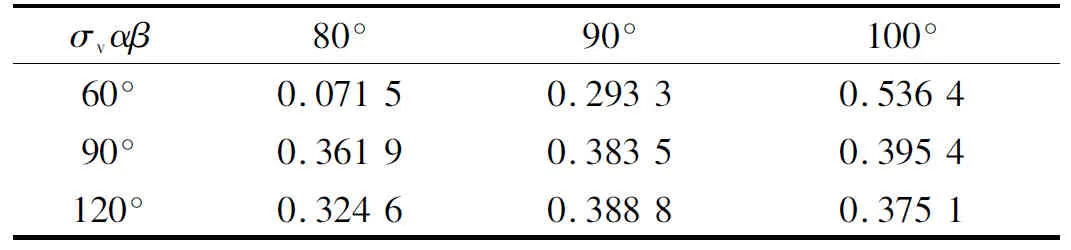
由表4、5可见,在α=60°、β=80°的情况下,无论兜孔弧面的半径大或小,保持架平均打滑率都是最低的,且明显低于其它情况;由表6、7可见,在α=60°、β=80°且Ru=3r0、Rh=3r0的情况下,保持架质心涡动速度偏差比明显低于其它情况,而由图5、6可见,在α=60°、β=80°且Ru=3r0、Rh=3r0的情况下,质心涡动轨迹的紊乱程度也明显低于其它情况,稳态情况下基本保持清晰的圆形。
4 结 论
(1)圆弧兜孔的弧面半径和弧面偏置角对滚子打滑和保持架涡动的影响显著。
(2)在高速轻载的工况下,当兜孔的弧面偏置角α=60°、β=80°时,无论弧面的半径大或小,轴承对滚子打滑的抑制效果都非常明显。
(3)在高速轻载的工况下,当兜孔的弧面偏置角α=60°、β=80°且弧面半径明显大于滚子半径(Ru=3r0、Rh=3r0)时,轴承对保持架涡动的抑制效果非常显著。
