基于基本尺度熵与GG模糊聚类的轴承性能退化状态识别

王 冰， 胡 雄, 李洪儒, 孙德建

(1.上海海事大学 物流工程学院，上海 201306；2.陆军工程大学石家庄校区 导弹工程系，石家庄 050003)

在机械设备维修理论中，基于状态的维修(CBM)能够以设备实时监测信息为基础，结合设备的结构与动力学特性，识别其运行状态，并对设备故障的演化趋势进行预测。从而弥补传统的事后维修与计划维修在维修效率上的不足[1]。CBM主要包括退化特征提取、退化状态识别、剩余寿命预测等关键技术[2-3]。

滚动轴承是机械设备中的重要的旋转支撑部件，旋转机械中约有30%的故障由滚动轴承引起。当前很多研究工作集中在轴承不同故障类型的特征提取和模式分类中[4-6]，而从CBM理论出发，分析滚动轴承性能退化规律，围绕退化特征提取和剩余寿命预测所开展的研究则相对较少。滚动轴承在性能退化过程中通常存在一个由正常到失效的发展过程，及时准确地识别其退化状态，能够合理地指导设备的检查和替换，从而提升整个机械设备的运行可靠性。对滚动轴承进行退化状态识别需要解决两个关键问题：①提取有效的退化特征；②建立科学的退化状态识别模型。

退化特征提取是实现退化状态评估的基础，主要目的是提取能够有效表征性能退化规律的特征参数。传统的退化特征主要基于时域、频域以及时频域分析方法提出。近年来，熵、分形等理论被逐渐应用在机械设备的退化特征提取中，为非线性信号演化规律的刻画提供了一条有效的途径。典型的退化特征指标包括提升小波样本熵[7]、层次熵[8]、LCD谱熵[9]、多尺度熵[10]、排列熵[11]等。在该类研究中，基本尺度熵[12]的提出为非线性信号的分析提供了一种全新的思路。基本尺度熵以符号动力学理论为基础，对心跳间隔序列进行幅值上的符号化，并计算熵测度。具有简单、快速和较强的抗干扰能力，可以有效地分析短时、非平稳、有噪声干扰的数据，该算法起源并有效地应用在心脏电信号分析中[13-15]，在机械设备故障诊断领域也有一些成功应用。例如钟先友等[16]提出一种改进的本征时间尺度分解方法(IITD)和基本尺度熵的齿轮故障诊断方法。首先采用IITD方法分解齿轮振动信号，计算前四个分量的基本尺度熵参数，以此作为故障特征向量；许凡等[17]提出了一种基于局部均值分解(LMD)与基本尺度熵的相邻传播(AP)聚类诊断方法，提取基于LMD与基本尺度熵的故障特征向量，并采用AP聚类算法实现滚动轴承的故障类型聚类。与此思路不同，本文将基本尺度熵理论应用在性能退化特征提取中，分析轴承性能退化过程中的基本尺度熵演化规律，从而为不同性能退化阶段的识别奠定基础。

性能退化状态的识别本质上是模式识别问题。机械设别的性能退化过程具有随机性、模糊性的特点，表现为退化过程不可预知，且退化阶段的数目与边界难以确定。聚类分析方法能够从退化特征数据的特点出发，挖掘数据之间的相似性关系，从而无监督地将数据划分到不同的类别中，是解决退化状态识别问题的有效途径。典型的聚类方法包括K均值聚类(K-means)、模糊c-均值聚类(FCM，fuzzy center means)、GK(Gustafaon-Kessel)聚类方法等。Wang等[18]采用数学形态分形维数作为轴承的性能退化特征，采用FCM算法实现了退化特征的自动聚类；Rai等[19]提出了基于EMD分解和K-means的退化状态聚类方法；黄友朋等[20]采用EEMD排列熵作为轴承的故障特征，并应用主成分分析和GK聚类方法实现了滚动轴承不同故障的自动聚类。

在无监督聚类算法中，GG聚类算法(Gath-Geva)对FCM和GK聚类算法进行了改进，引入了基于模糊最大似然估计的距离范数，从而能够反映不同形状和方向的数据类别，聚类的精度和准确性更高。张立国等[21]应用本征时间尺度分解模糊熵和GG模糊聚类方法对滚动轴承进行故障诊断，取得了较FCM、GK算法更优的聚类效果。Li等[22]提出了基于VMD分解和GG聚类的退化状态评估方法，采用GG聚类算法对时间序列进行分割。Yu等[23]首先采用EEMD和SVD方法提取滚动轴承的故障特征，并结合GG聚类方法，对不同的故障状态进行聚类。在关于GG聚类算法的研究中，研究热点主要集中在故障模式的诊断中，对性能退化状态的聚类则相对较少，并且并未考虑性能退化状态中的时间连续性约束，算法的针对性还需要进一步研究。

综上，本文对分别采用基本尺度熵和GG聚类算法解决滚动轴承退化状态识别中的两个关键问题。分析轴承性能退化过程中的基本尺度熵演化规律，并建立融入时间约束的退化特征向量，并采用GG聚类算法实现不同退化状态的识别。采用IEEE PHM 2012的轴承全寿命数据集进行实例分析，对比验证本方法的有效性和优越性。

1 相关理论基础

1.1 基本尺度熵

一维信号的基本尺度熵计算思路如下：首先对数据进行从1维到m维的矢量转换，然后根据基本尺度参数a将m维矢量转换为相应的符号序列，最后由符号序列统计出相关概率并计算基本尺度熵值。具体计算过程如下。

假设u为长度N的一维时间序列，首先将其u转换成为m维矢量X，转换方式如下

X(i)=[u(i),u(i+L),…,u(i+(m-1)L)]

(1)

式中:m为矢量维数，L为延迟因子，i+(m-1)L≤N。当L=1时，u可以转化为N-m+1个m维矢量。之后，对每个m维矢量进行符号化，将其转换为m为矢量符号序列S

Si(Xi)={s(i),s(i+L),…,s(i+(m-1)L)}

(2)

式中:s∈A:A=0,1,2,3，转换过程如下[24]

(3)

(4)

式中:a为基本尺度参数，在实际应用中需要合适地选择。取值过大会丢失信号中的细节信息，无法反映信号的动态变化信息，取值过小则会受噪声影响。

最后，统计m维矢量符号序列S的分布概率P(Si)。由于包括四种符号，所以m维矢量符号序列共有4m种不同组合状态π，因此，整个N-m+1个m维矢量中所占的概率为

(5)

式中，1≤t≤N-m+1，#表示个数。

计算序列u的归一化的基本尺度熵如下

(6)

基本尺度熵描述了时间序列中m个取值所包含的波动信息，即信息的复杂度。基本尺度熵值越大，则表明序列维矢量的波动模式越复杂，序列的复杂性越高；反之，熵值越小，序列的复杂性越低[25]。

一般情况下，延迟因子默认为L=1；矢量维数m可以取3～7之间的任意整数，序列长度N应该大于4m。

1.2 GG模糊聚类

1.2.1 GG模糊聚类

GG模糊聚类对FCM和GK聚类算法进行了改进，引入了基于模糊最大似然估计的距离测度，算法过程如下。

假设聚类样本集合为X={x1,x2,…,xN}，集合内的元素xk(k=1,2,…N)具有d个特征指标，即xk{xk1,xk2,…,xkd}，对X聚类的目标是将其划分为c类。假设每个分类的聚类中心向量为V={v1,v2,…,vc},假设隶属度矩阵为U=[μik]c×N，其中元素μik∈[0,1]表示第k个样本对第i类的隶属度(i=1,2,…,c)。GG模糊聚类通过迭代(U,V)，使目标函数Jm取得最小值。

(7)

式中:M为加权指数，M>1，M越大，各个类别之间的重叠越多，一般取2。迭代调整的步骤如下[26]

(1) 计算聚类中心

(8)

(9)

其中Ai代表第i个聚类的协方差矩阵。

(2) 更新分类矩阵

(10)

其中，i=1,2,…c;k=1,2,…N.

1.2.2 聚类效果评价

为了对聚类算法的效果进行评价，一般采用分类系数和平均模糊熵两个指标。此外，为了评价性能退化状态识别中分类样本在时间特征上的连续性，本文提出时间一致度指标。三种指标的定义如下。

(1) 分类系数CC(Classification Coefficient)。该指标定义为隶属度的方均值，计算方法如下。其中uik代表隶属度数值，分类系数越接近1，聚类效果越好。

(11)

(2) 平均模糊熵AFE(Average Fuzzy Entropy)。该指标定义为隶属度分布所蕴含的信息熵大小，计算方法如下。其中uik代表隶属度数值，平均模糊熵越接近0，聚类效果越好。

(12)

(3) 时间一致度TC(Time Consistency)。该指标定义为样本在时间特征上的序列偏离度。计算方法如下：

首先定义序列偏离度，该参数定义为序列当前排列与顺序排列之差的和，用于表征序列的乱序程度。例如序列[1,2,3,5]的序列偏离度为1，序列[6,7,8,9]的序列偏离度为0。

假设目标样本集合X={x1,x2,…,xN}被划分为c类。隶属于每个类的样本集合为S={s1,s2,…,sc}, 其中bi(i=1,2,…,c)代表所有隶属于si(i=1,2,…,c)的样本在时间特征维度的序列偏离度。时间一致度指标定义为所有类别序列偏离度的算数平均值，计算如下。该指标越接近0，代表序列的时间聚集度越高，聚类效果越好。

(13)

2 基于BSN-GG的退化状态识别方法

研究表明，滚动轴承在性能退化过程中一般会经历从正常到失效等多个退化状态[27]。为了分析轴承在全寿命实验中的性能退化规律，识别不同阶段的轴承性能退化状态，本文将基本尺度熵与GG聚类方法相结合，提出一种基于BSE-GG聚类的退化状态识别方法。该方法的基本流程,如图1所示。

(1) 轴承全寿命数据集获取与划分。

采用在线监测的方式获取滚动轴承从良好到失效的全寿命振动信号。考虑到全寿命实验时间长且数据量大，一般采用间隔采样的方式，将每组采样所获取的振动数据依次记作Group1、Group2，直到GroupN轴承失效。

(2) 退化特征提取

以组别为单位对振动信号进行退化特征提取，计算每组数据的基本尺度熵和有效值RMS，以此作为描述轴承性能退化规律的特征指标。与此同时，考虑到同一性能退化状态在时间上的连续性，将时间t作为退化特征指标描述该过程的时间规律。进而构建三维特征指标[BSE; RMS;t]。

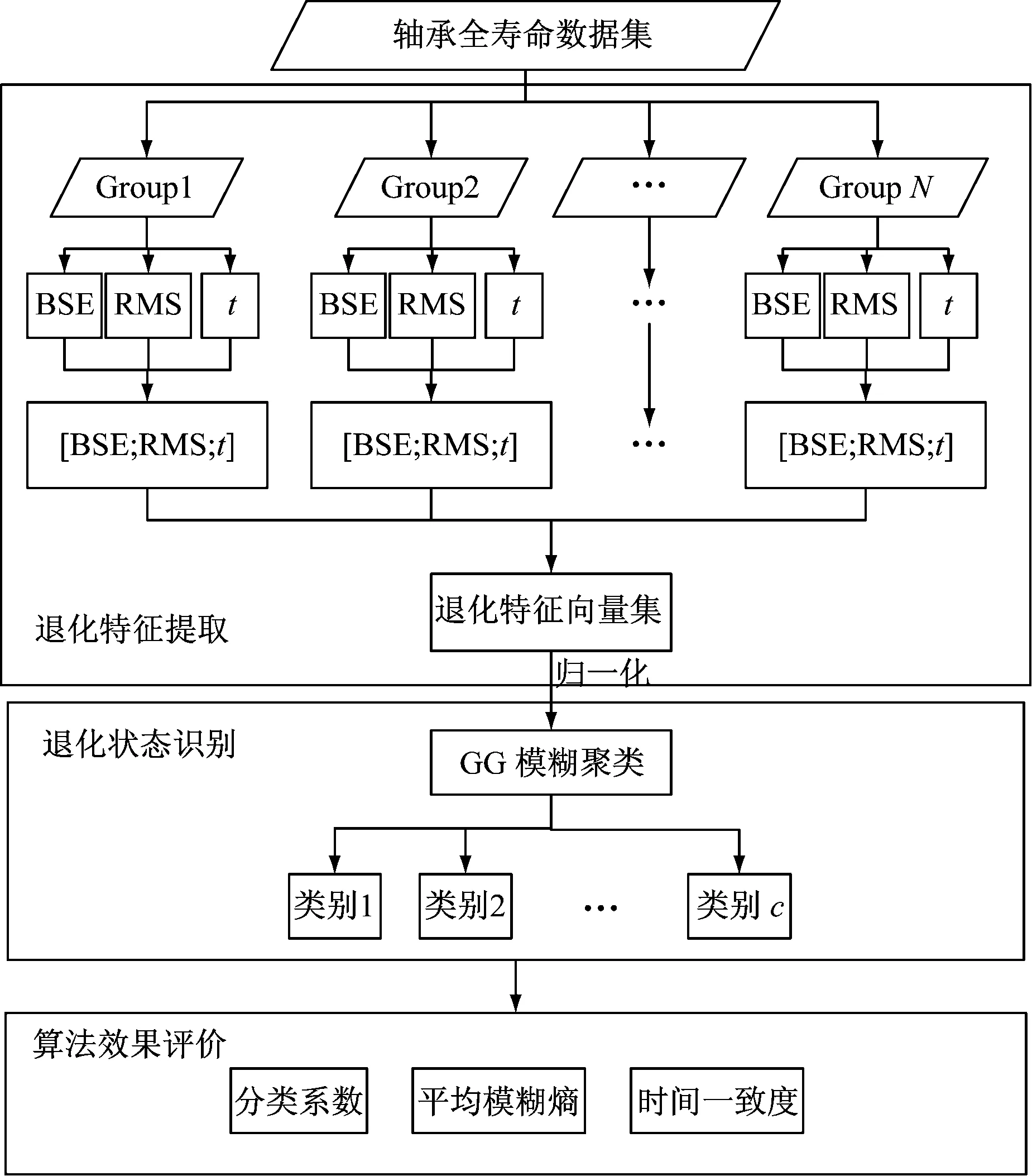
图1 基于BSE-GG聚类的退化状态识别流程

(3) 退化状态识别

采用GG聚类算法对退化特征向量进行聚类。从而识别轴承性能退化的不同状态。

(4) 识别效果评价

分别采用分类系数、平均模糊熵、时间一致度对GG聚类算法的聚类效果进行评价，并对比其他同类算法的效果。

3 实例分析

3.1 数据集

本文选用的轴承全寿命数据集来自IEEE PHM2012所提供的数据集[28]。试验在FEMTO-ST研究中心的PRONOSTIA试验台进行。通过运行在不同负载条件下的加速退化试验，获取多组从良好到失效的轴承全寿命振动信号。试验台的实景图,如图2所示。

在加速退化试验中，分别采集转子输出轴垂直方向(vertical axis)与轴向(horizontal axis)的振动信号，振动传感器选用DYTRAN超小型加速度传感器3035B，振动传感器布置和选型,如图3所示。

本文选取三组全寿命试验数据集的V向振动数据进行分析，系统采样频率为25.6 kHz，每组的采样时间为0.1 s，组间采样间隔为10 s。数据集基本描述见表1。

图2 加速试验台实景图

图3 振动传感器布置与选型

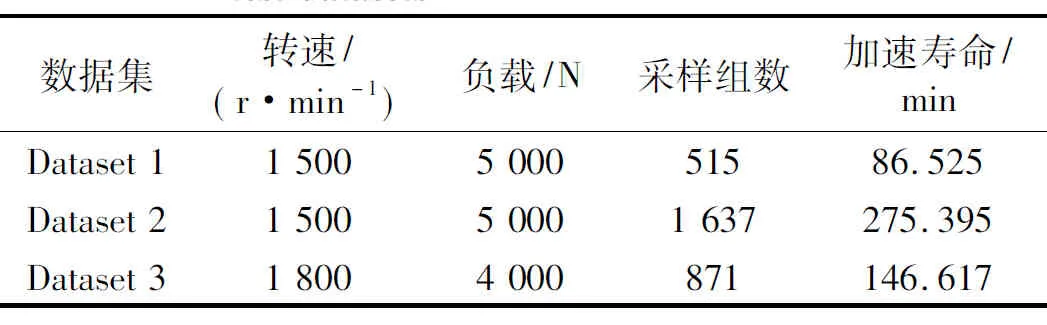
忽略三组数据集的采样间隔，从信号的时域波形分析性能退化过程。如图4所示。可以看出，三个数据集在寿命的前期和中期均保持相对稳定的状态，后期振幅逐渐增大，直至轴承失效。相对而言，数据集Dataset 3在寿命中期存在明显的冲击成分。

3.2 基于BSE的退化特征提取

提取三个数据集中每组振动信号的退化特征。依次计算其基本尺度熵和有效值。在基本尺度熵的计算过程中，通过多次对比发现，改变m值从3到7，ɑ值从0.1到0.6，结果没有明显区别，因此取m=4，ɑ=0.2。三个数据集的基本尺度熵和有效值计算结果分别如图5～图7所示。

以图5为例进行分析。在轴承的性能退化过程中，基本尺度熵在整体上呈现单调上升的趋势，并表现出一定的阶段性特点，反映出轴承性能退化的不同阶段。在第55组采样点之前，BSE保持相对稳定的状态，取值保持在0.55左右。从第55到第490组采样点之间，BSE呈现出一个缓慢的上升过程，BSE取值从0.6缓慢上升至0.72左右。在第490组采样点之后，BSE出现一次明显的阶跃上升过程，取值保持在0.75左右，此时认定轴承已失效。与之相对应，有效值在整体上上升且阶段性特点明显，但在第55组采样点左右存在一个明显的下降趋势，分析认为该阶段可能处于轴承的磨合期，导致BSE和有效值表现出不同的规律性。对比图6和图7中其他两个数据集的分析结果，可以得到同样的结论。综上，基本尺度熵在轴承性能退化过程中体现出整体单调性的特性，并且对轴承退化状态的变化十分敏感，能够较好地反映轴承性能退化的规律性。因此，选择基本尺度熵作为性能退化特征指标是有效的。

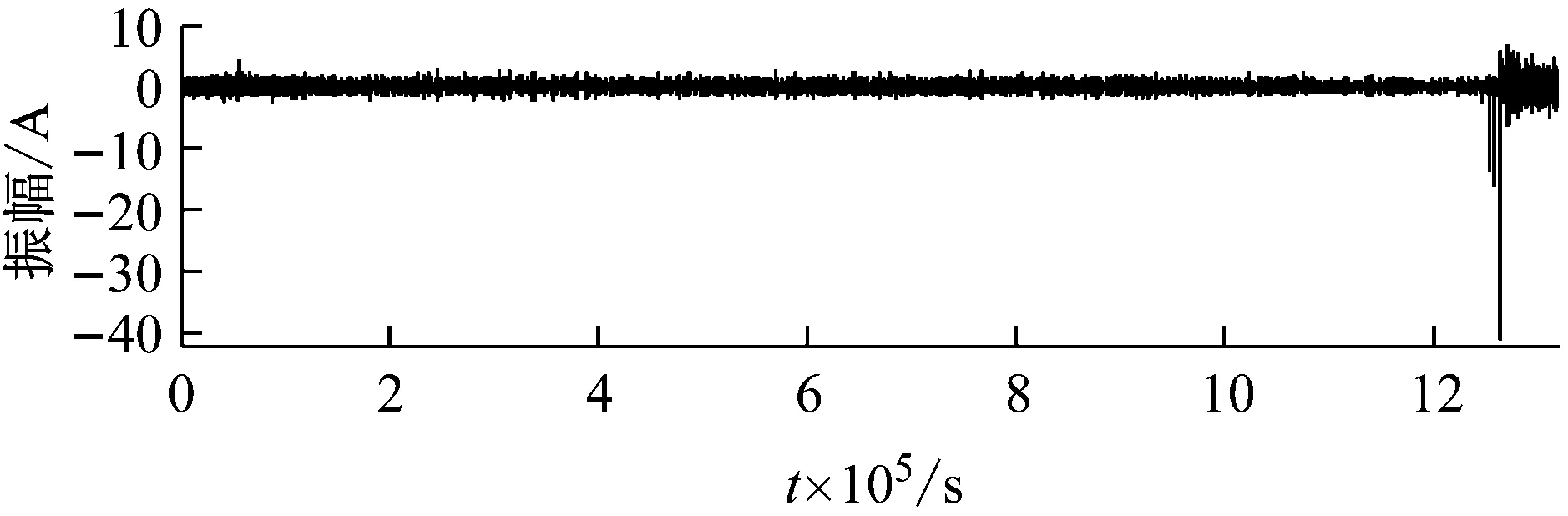
(a) Dataset1

(b) Dataset2

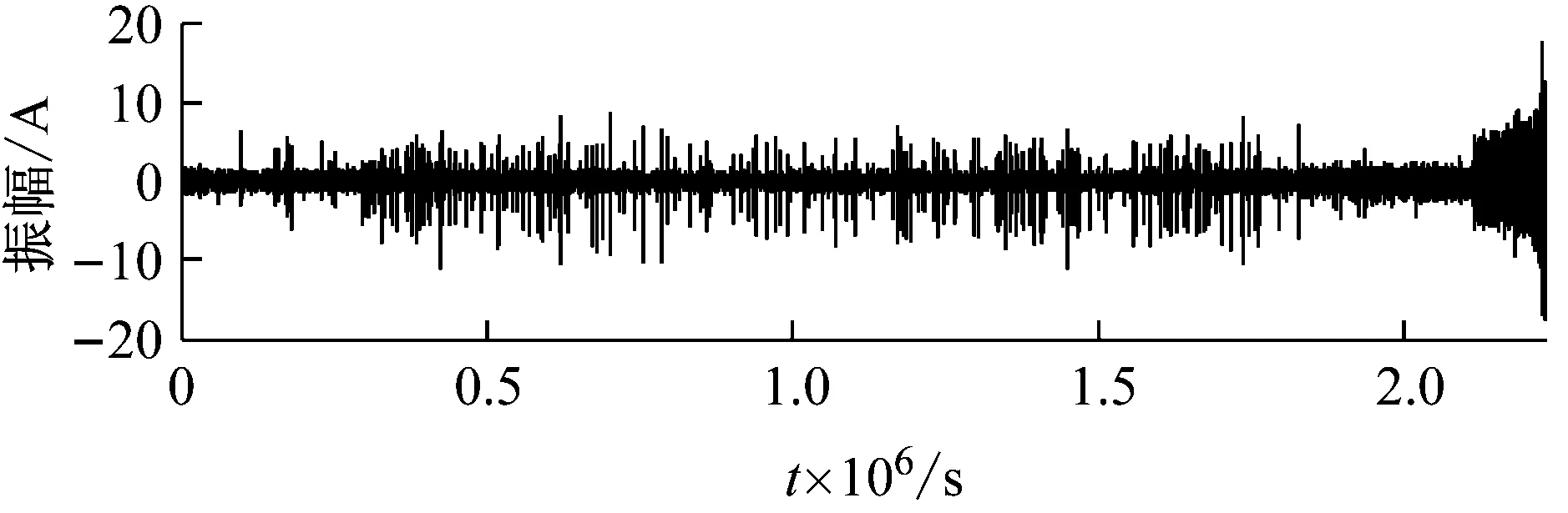
(c) Dataset3

3.3 基于GG聚类的退化状态识别

以数据集Dataset1为例进行退化状态识别分析。经过退化特征提取，构建该数据集515×3的退化特征向量集，归一化之后，采用GG聚类方法对性能退化状态进行聚类。根据上节的初步分析，设置聚类组数c=3，加权指数M=2。根据算法迭代效果，经过多次试验对比，取容差参数为ε=0.000 1。迭代更新退化状态的聚类中心，直至算法收敛。选用FCM和GK聚类算法进行对比分析，三种算法在BSE和RMS二维坐标上的等高线聚类效果如图8所示，其中“O”为聚类中心。可以看出，GG聚类的样本重叠程度最低，等高线为任意形状，而FCM聚类和GK聚类的等高线分别接近于圆形和椭圆形。这说明GG聚类算法中基于模糊最大似然估计的距离测度能够更灵活地划分聚类结构，对数据源的分布要求最低。而FCM聚类和GK聚类算法均以欧式距离为基础建立距离测度，能够更好的适应近似圆形分布的聚类结构，对数据源的分布要求较高。

(a) 基本尺度熵

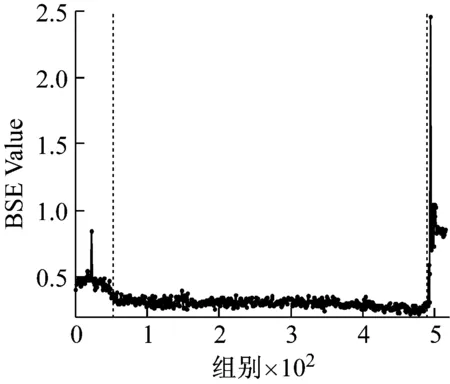
(b) 有效值

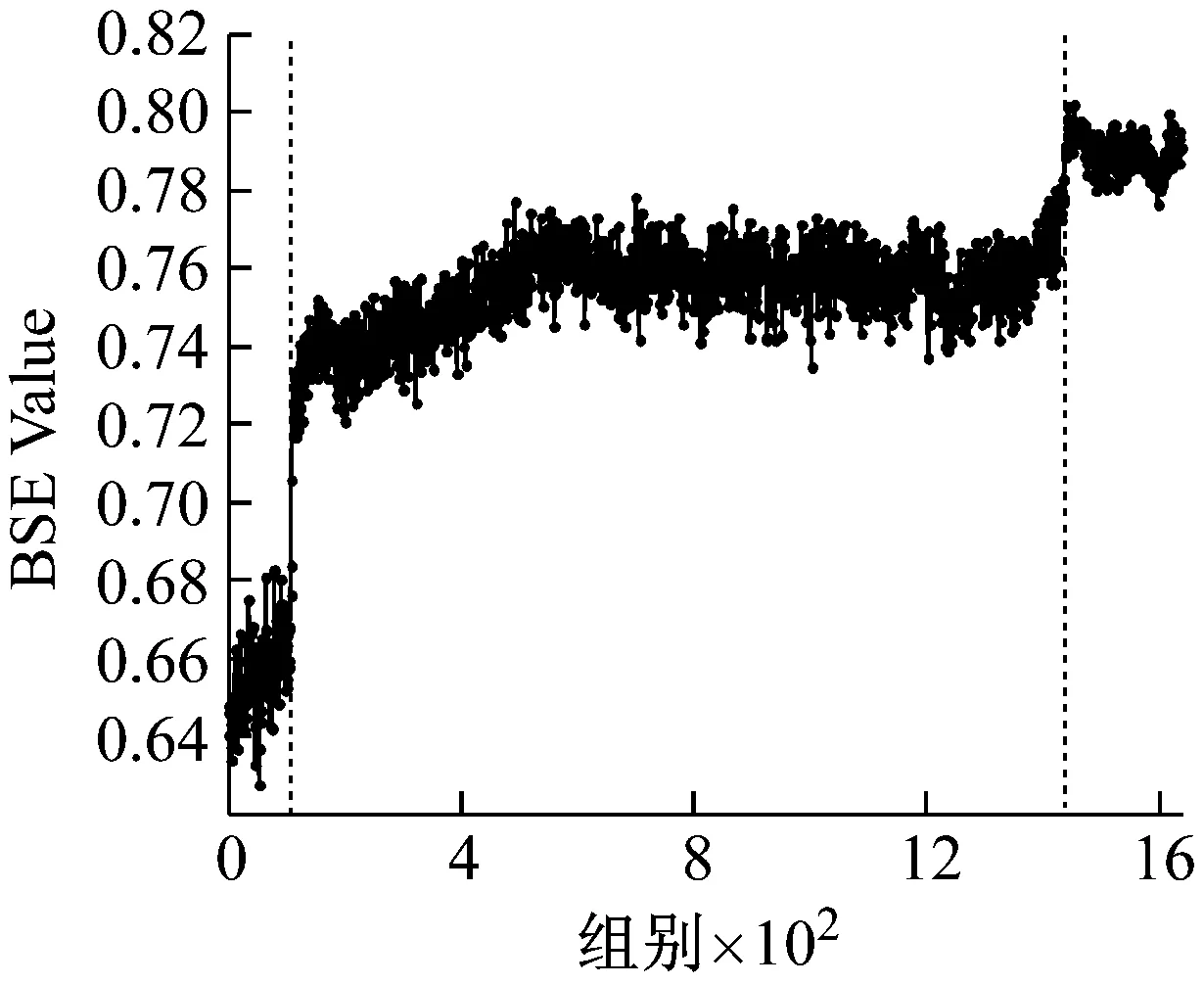
(a) 基本尺度熵

(b) 有效值

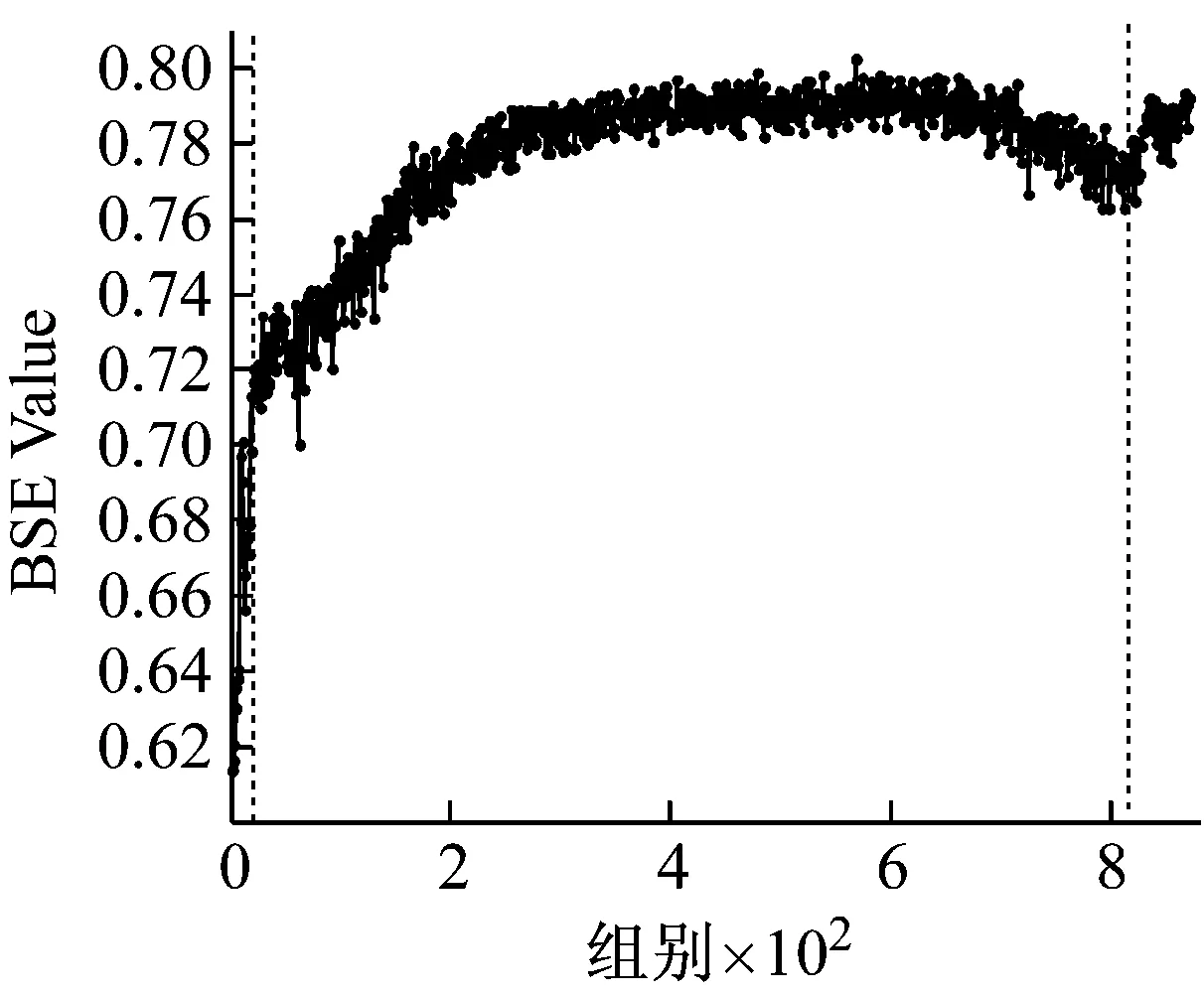
(a) 基本尺度熵

(b) 有效值

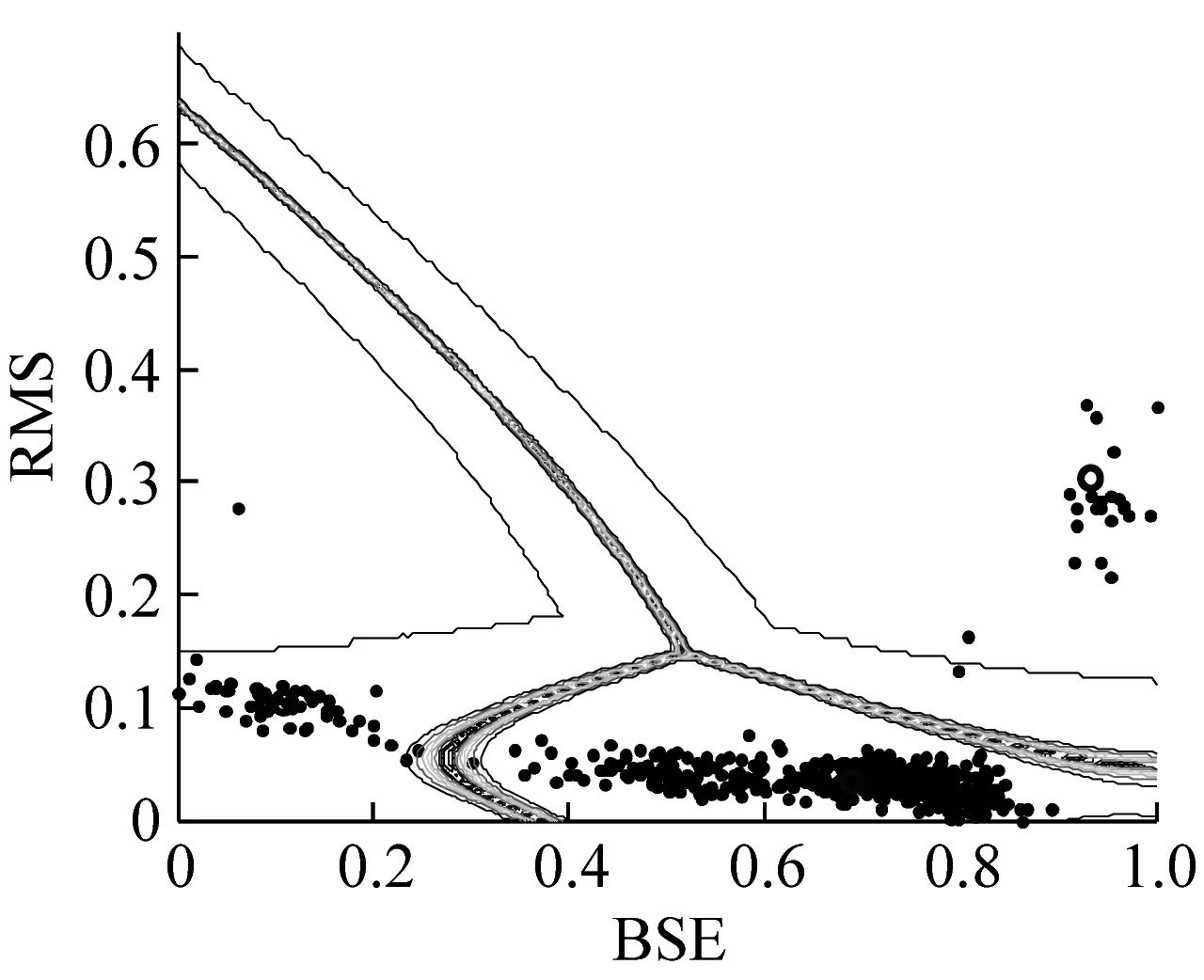
(a) GG聚类算法等高线

(b) FCM聚类算法等高线

(c) GK聚类算法等高线

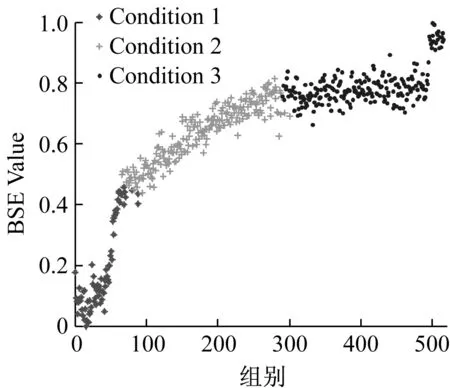
图9～图11描述了三种算法对Dataset1的三维和二维聚类效果。可以看出，三种聚类算法均将数据集识别为三类，根据前文的分析，将其分别定义为Condition1(磨合期)、Condition2(稳定期)、Condition3(失效期)。定性对比分析，GG聚类算法能够较好地识别特征曲线的主趋势和突变点，符合对退化状态的直观分析。而FCM算法则将大部分稳定期的数据识别为失效期，GK算法则将磨合期的时间估计的更长。

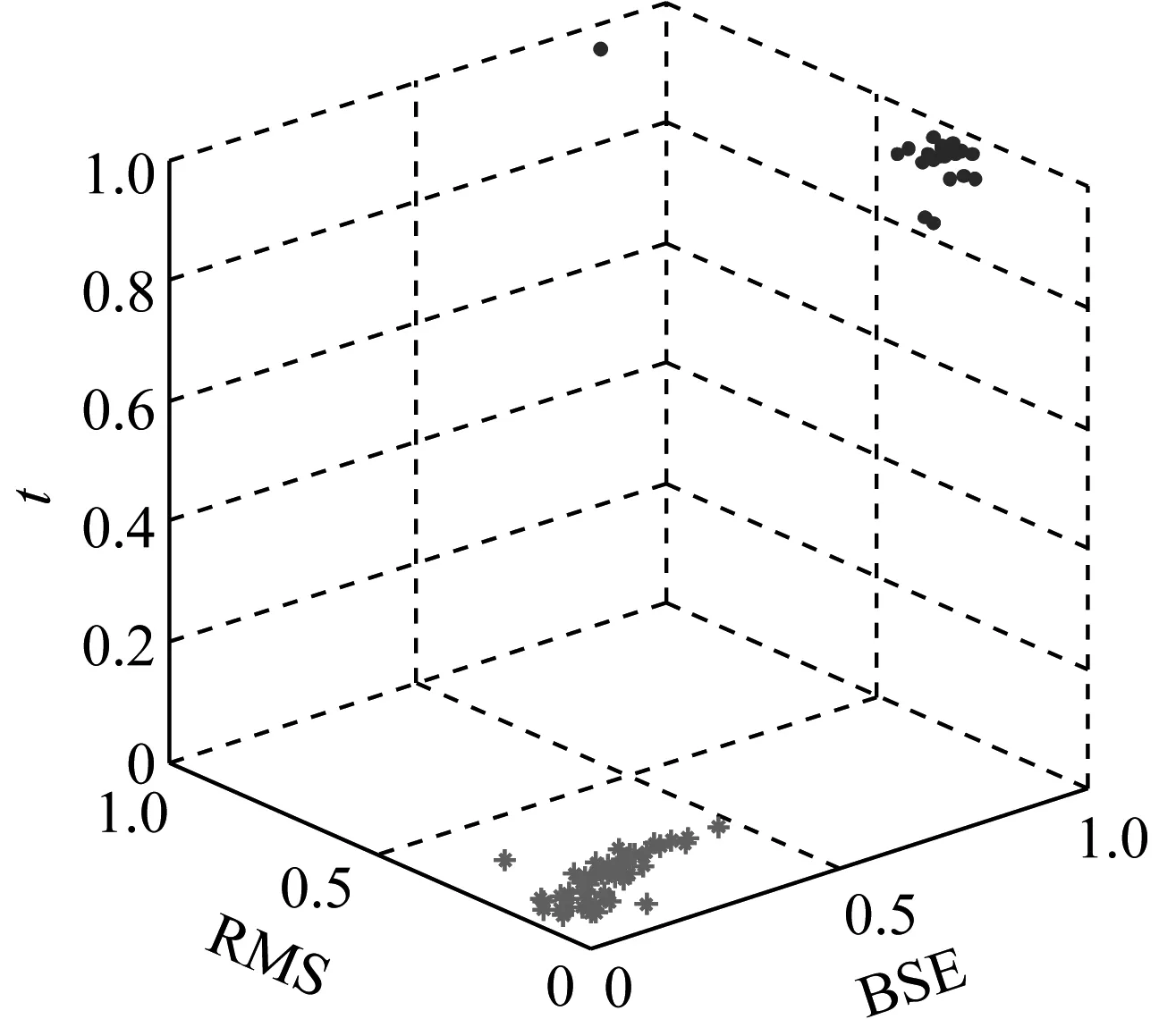
(a) 三维聚类效果

(b) 二维聚类效果

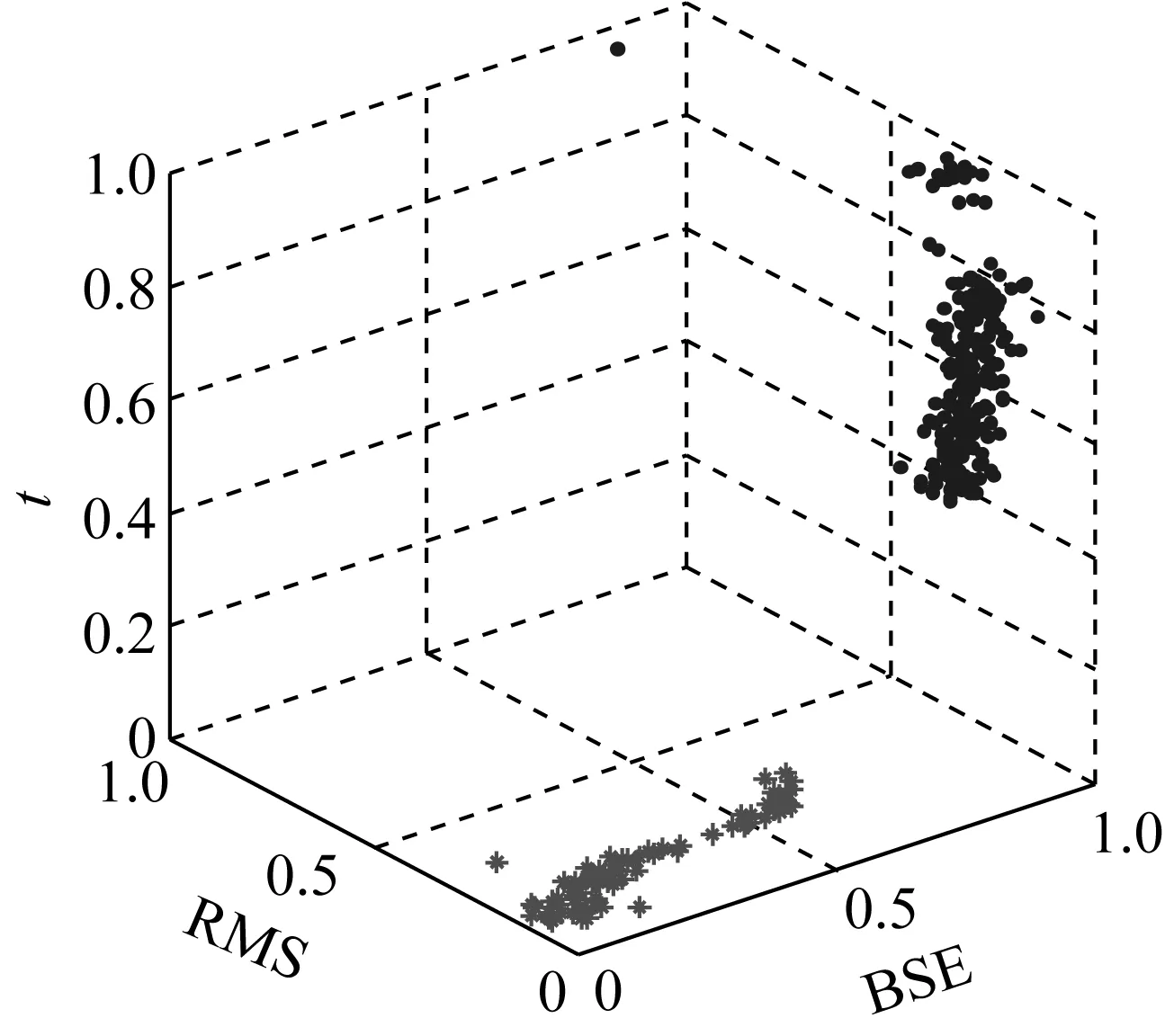
(a) 三维聚类效果

(b) 二维聚类效果

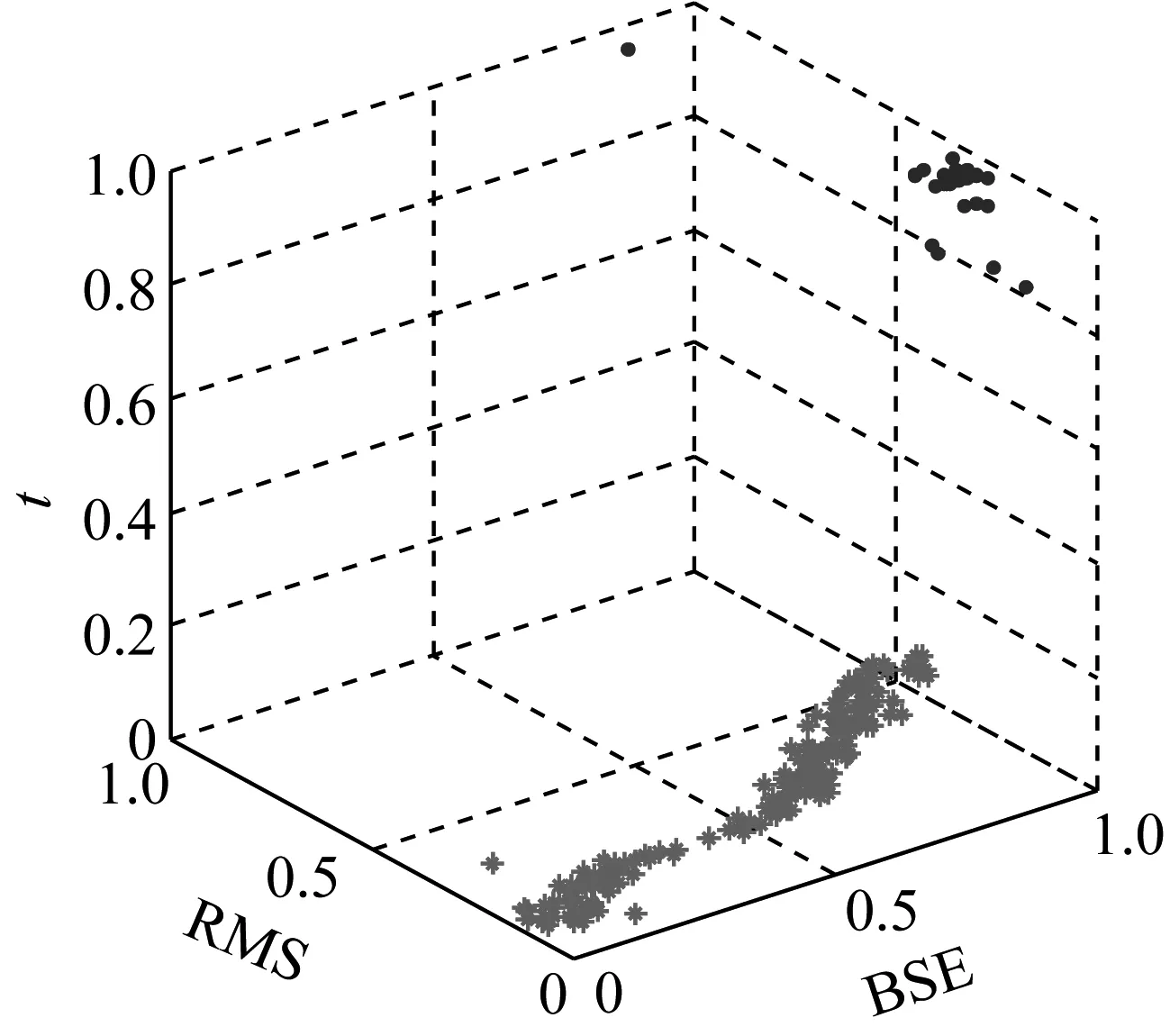
(a) 三维聚类效果

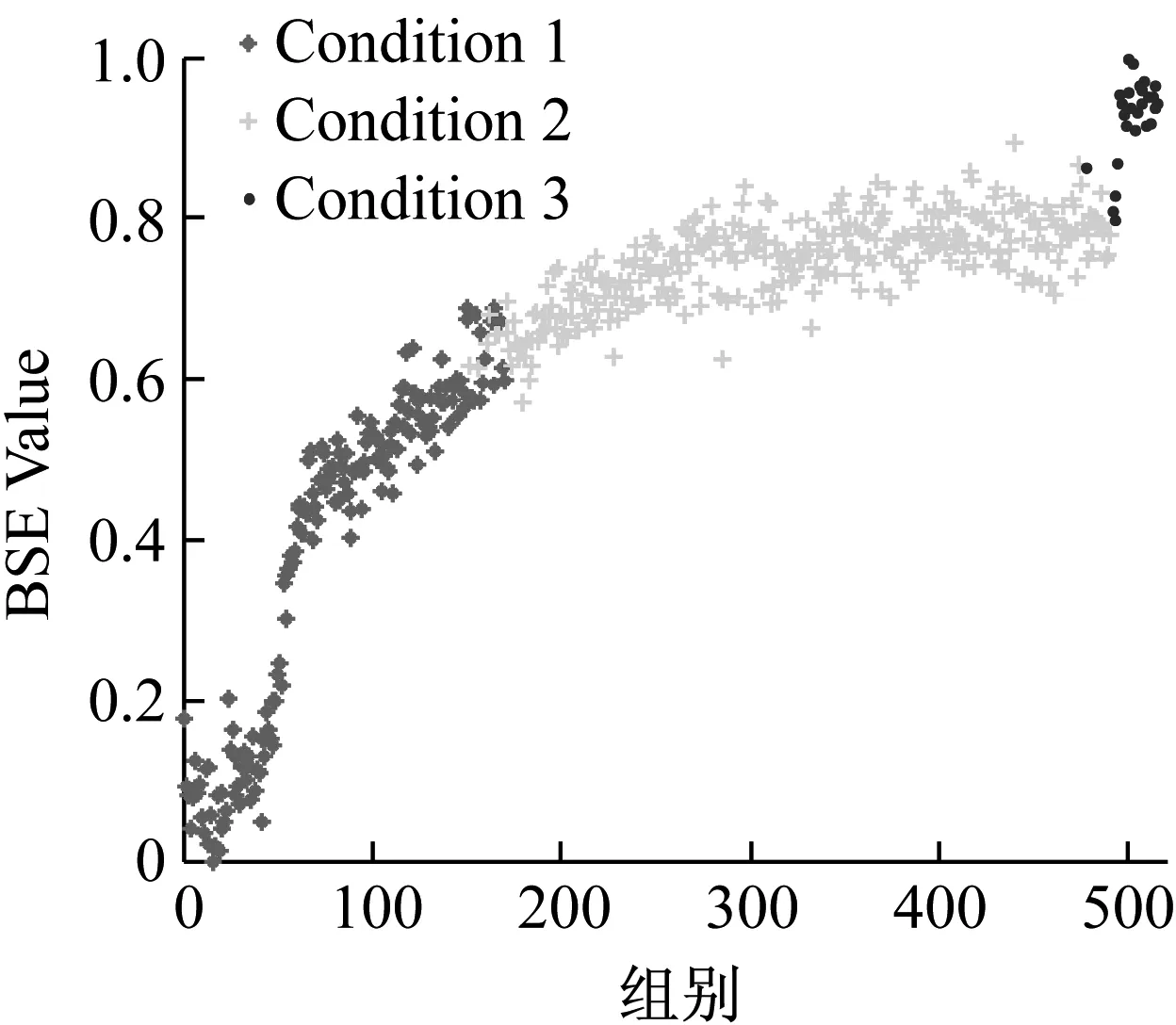
(b) 二维聚类效果

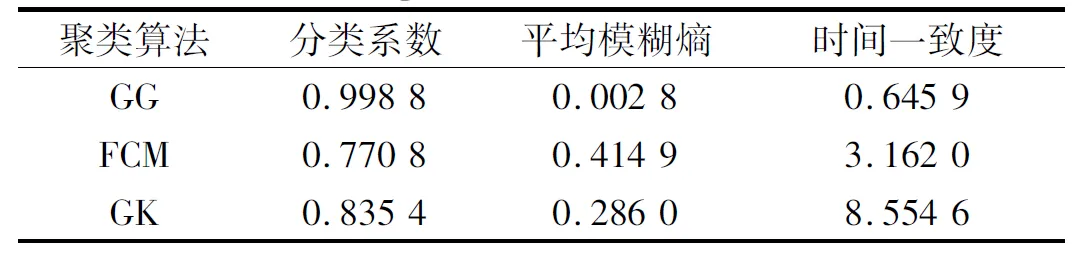
表2定量分析了三种算法对Dataset1的聚类效果。GG聚类算法的分类系数取值最高，平均模糊熵和时间一致度最低，聚类效果最优。相比而言，FCM聚类算法的聚类效果最差，但GK聚类结果的时间一致度最差。

采用GG聚类算法对数据集Dataset2和Dataset3进行分析，为了分析时间特征向量对于聚类效果的影响，分别采用三维特征向量[BSE;RMS;t]和二维特征向量[BSE;RMS]进行聚类分析，三种算法的定量聚类结果如表3所示。由于聚类结果相近，为了清晰地分析其细节，均以基本尺度熵特征上的聚类效果为例进行对比分析，如图12和图13所示。可以看出，两种方法的分类系数和平均模糊熵指标相近，但三维特征向量的选取能够明显的提高聚类结果的时间一致度。对于Dataset3的识别效果对比更为明显，如图13(a)所示，Condition3的几个数据点零星地分布在Condition2的连续时间尺度内，使得时间一致度达到204，使得序列的一致性最差。这说明，时间特征参数的约束能够

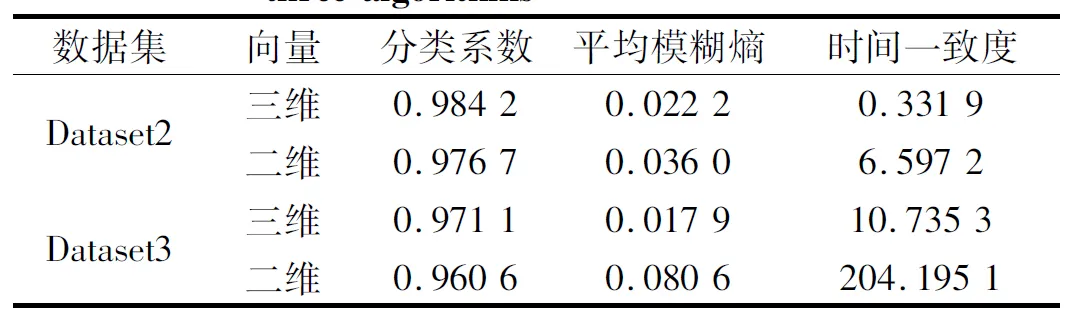
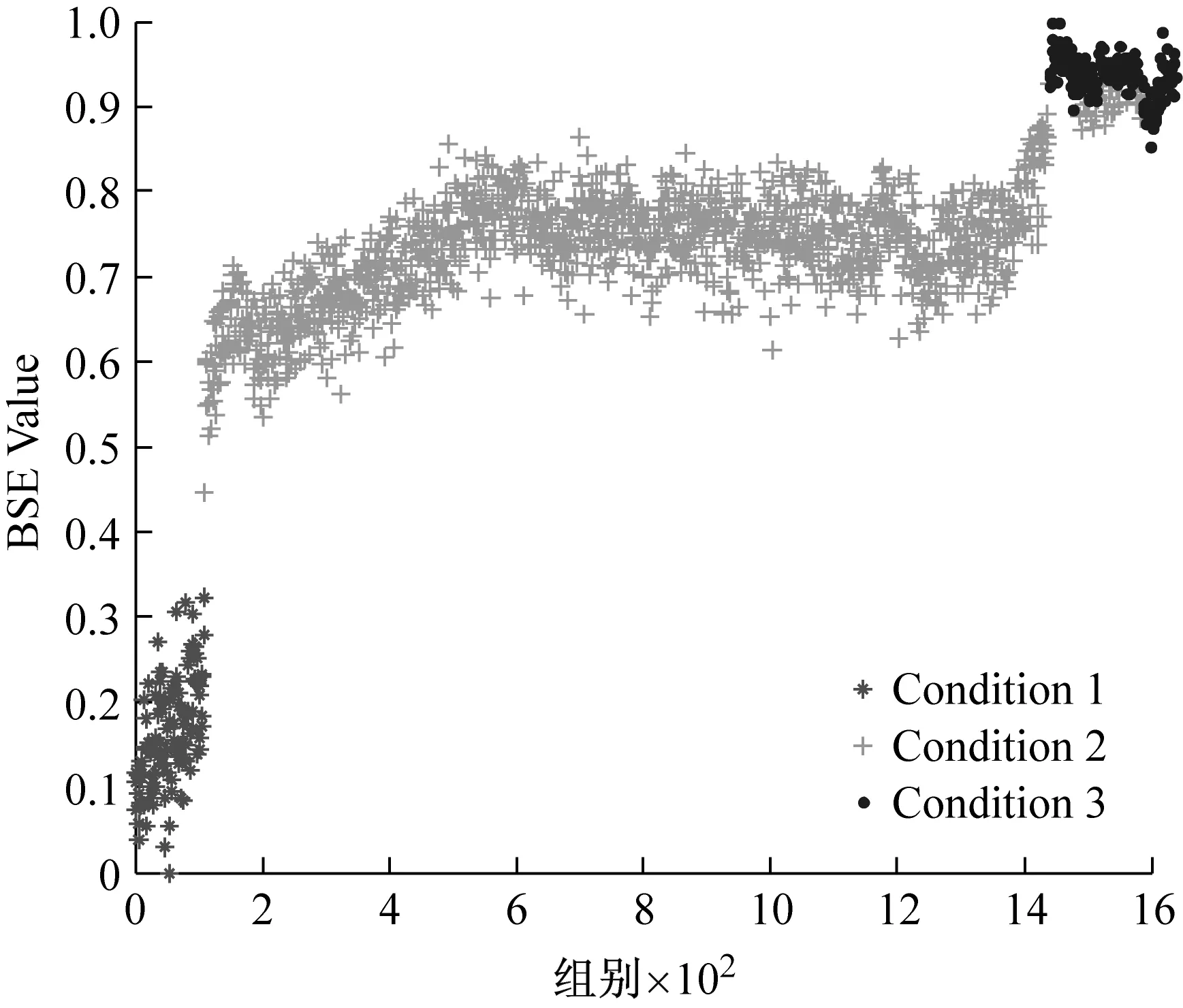
(a) 二维特征[RMS;BSE]

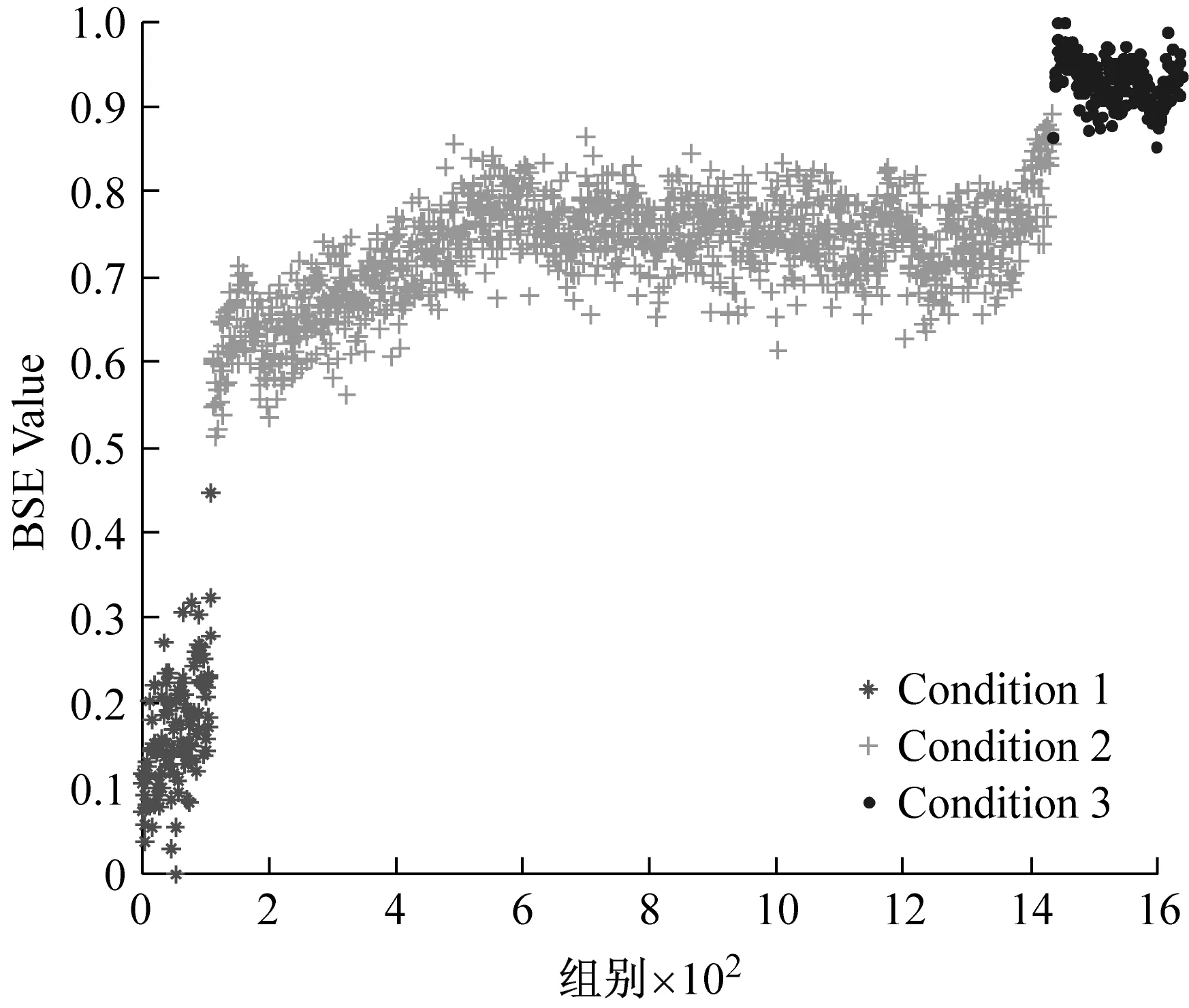
(b) 三维特征[RMS;BSE;t]

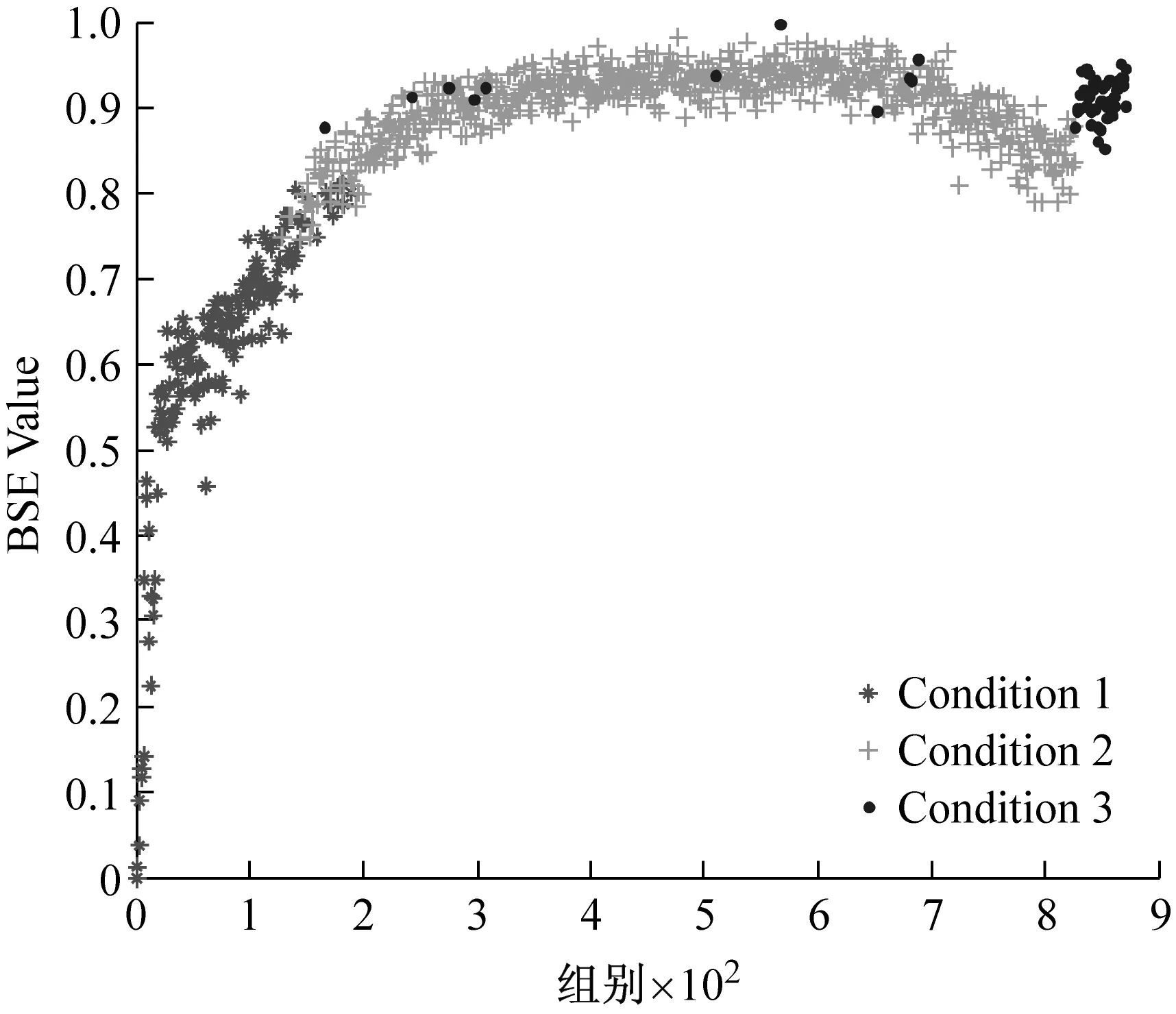
(a) 二维特征[RMS;BSE]

(b) 三维特征[RMS;BSE;t]

在GG聚类过程中考虑数据点之间的时间维度距离，从而提高类别内部的时间聚集度，聚类效果更优，满足对性能退化状态识别的要求，从而验证了该方法的有效性和优越性。

4 结 论

本文提出一种基于基本尺度熵与GG聚类的退化状态识别方法，通过对实例数据的分析验证，得到以下结论：

(1) 基本尺度熵能够反映信号在基本尺度内波动模式的复杂程度，从而刻画轴承在性能退化过程中的复杂性演化规律。并且呈现出主趋势单调性、变化敏感性的特点，是一种有效的性能退化特征提取方法。

(2) GG聚类方法能够对任意形状的数据进行聚类，将时间约束加入到特征向量中，能够在保持聚类精度的同时，提高类别内部的时间聚集度。所提出的时间一致度参数较好地反映出了聚类的时间聚集效果。

(3) 退化状态数目的不确定性一直是该领域的研究难点。文中通过先验知识对GG聚类算法的参数c进行设置，取得了与直观分析相一致的结果。下一步有必要深入退化状态数目的智能选取方法。