小学数学教学中以“旧”引“新”的教学策略
2019-03-25浙江省杭州市余杭区良渚古墩路小学孙潇潇
浙江省杭州市余杭区良渚古墩路小学 孙潇潇
在数学课堂教学中,教师往往会考虑如何设计活动,让学生在体验操作中获得新知,会考虑从学生的学习兴趣、学习动机的激发角度去设计教学,于是我们的课堂开始往往会有动听的音乐、精彩的视频、激动人心的游戏。虽然这些设计很是富丽堂皇,学生也非常喜欢,但学生喜欢的并非是教学内容本身,而仅仅是跟教学内容关系不大的一些额外的活动。这样的教学为学生建立的学习兴趣是肤浅而不持久的,而且有一个重要的缺陷,即忽视了学生已有的数学活动经验,忽视了学生的认知水平,即忽视了教学的本质,忽视了新旧经验的连接来预设教学活动,这样的教学方式因其表面的华丽,最终会产生巨大的副作用,最终只会扰乱学生的数学思维,大大地消减学生的学习兴趣,使他们得不到良好的发展,使教学等不到高效。
《义务教育数学课程标准(2011年版)》中指出:教师教学应该以学生的认知发展水平和已有经验为基础,面向全体学生,注重启发式教学和因材施教。大数据背景下的学生,成长的道路变得非常宽广。立足于学生已有的知识经验、已有的活动经验、已有的数学思想,对接新的数学知识,让学生脑海中的数学知识呈螺旋式的阶梯呈现。
一、借助学生已有的知识技能,精准铺垫新知教学策略
通过前后知识的联系,给学生的头脑中建立一个完整的认识结构,让学生在有限的时间里学得明白、学得透彻、学得轻松。对学生来说,通过教学把前后的知识有效串联起来,既能让学生掌握新的知识,又能领会到数学知识的本质。
案例1:在进行《异分母分数加减法》的教学时,先复习巩固一下整数与小数的加减法来铺垫本课教学是老师常见的做法。我们来分析两位老师的做法:
甲老师先出示了两个计算题:526+26,35.4+14.3,然后让学生计算并校对答案,由于学生的答案正确率极高,教师就马上让学生总结算法——相同数位上的数相加。乙老师先出示的是:720+72,366+16.6,再让学生说说怎么算 。学生认识到第一题中如果拿2与2相加,会导致数位错位,算理上无法解释,正确的算法应该是将720个位上的0与72个位上的2相加,再依次计算。同样,第二题中直接把两个数的三个数位依次对齐,也就是366个位上的6与16.6小数点后十分位上的6相加,也会导致违反算理,只有把366的十分位补出来,写成366.0,然后再分析两个数的相同数位分别是什么,再依次把相同数位上的数相加,才能得出正确答案。这样学生就非常牢固地复习了相同数位对齐的概念,为后续教学打下了扎实的基础。
同样的环节设计,实际上都是为了唤起学生已有知识,为探究异分母分数加减法的算理埋下伏笔,两位老师总结的算法也一样,看似都没有问题,但很明显第二位老师棋高一着,他有意地出示了两道易错题,让学生分析得出:小数加减法和分数加减法之间算理相同,关于计算既不是想怎么对齐就怎么对齐,也不是“末位对齐”,而是实实在在的相同数位对齐。在第一位老师的教学中,不少学生其实在头脑中巩固的并非是完全扎实的计算方法,有一部分学生是借助“末位对齐”的方法凑巧而答对的,给了他们浑水摸鱼的机会。由此可见,我们在拿已有知识技能为学生新知识学习做铺垫时,必须有精准的算理与科学的方法,要防止算理跑偏,方法走调。
二、巧用学生已有的活动经验的教学策略
学生利用已有的数学活动经验,不仅能迅速找到新知的抛锚点,而且能辨别新旧知识的异同。从学生已有的活动经验为切入点,给学生创造思考的机会,鼓励学生猜想、发现,让学生对已有的数学活动进行迁移转化,构建新的活动经验。
案例2:为了教学有括号的混合运算题,教师出示:9.8-0.4+0.9与9.8-(0.4+0.9),请学生选择一个自己喜欢的算式,编一个情景。
生:我选择第二个算式。小明口袋里有9.8元,他买橡皮用去0.4元,买铅笔用去0.9元,还剩多少钱?
师:如果我给第1个算式补上小括号,大家有什么发现?
生:跟刚才那道题一样了。
师:现在大家计算一下这两个式子,结果一样吗?
生:计算结果不一样。小括号不可以乱填,会改变运算顺序。
师:用我们学过的方法,把第2个算式中的小括号去掉,应该怎么写?
生:9.8-0.4-0.9。
师:这是简便计算教学中连减的性质。在刚才的问题中,为什么9.8-(0.4+0.9)与9.8-0.4-0.9的计算结果相同呢?
生:因为9.8-(0.4+0.9)表示的是小明口袋里有9.8元,他买橡皮用去0.4元,买铅笔用去0.9元,他一共用去了(0.4+0.9)元,也就是1.3元,然后拿总钱数9.8减去用去的1.3元算出剩下的钱数。而9.8-0.4-0.9表示的是拿9.8元买橡皮用去0.4元,算出剩下的钱,再把剩下的钱买铅笔,又用掉了0.9元,由于总钱数一样,买的东西一样,用掉的钱数也一样,所以剩下的钱数当然是相同的。
师:所以这两个算式是计算顺序不同,表示意义也有不同,用不同的算式来表示同一回事,它们的结果是相同的。
教师在这段教学中很好地把握了学生在简便计算中已经涉及的算法,但其实学生只是一种语言形式的技巧,掌握并不牢固,至少没有形成内心的理解,于是老师再次挖掘学生,把握学生的认知起点,对接学生的生活经验、活动经验,并对学生头脑中的数学经验进行教学辅助,让生活经验和教学经验“无缝对接”,帮助学生生成新的教学体验。对于一些比较抽象的数学问题将之生活化,我们会发现学生在理解上、思考上都会比较顺畅。这就是数学的本质,数学来源于生活,应用于生活。
三、着力学生已有的数学思想的教学策略
在数学教学中,把培养学生用数学思想去思考问题,用数学知识去解决问题作为数学学习的核心目标,就是让学生遇到问题会想数学、用数学。通常在数学教学中,教师会引导学生通过观察、尝试、估计、归纳、类比、画图等数学活动发现数学规律,猜测数学结论,发展学生的数学逻辑推理能力,积累和提升策略性与方法性的经验。
案例3:有一个数是“几万几千”的形式,它的百、十、个位都是0,省略万后面的尾数得到近似数是8万,那么这个数最小是( ),最大是( )。
师:想一想可以通过什么方法表示出8万?(生纳闷)小明家住八楼,小强家与小明家住同幢楼的九楼,大家想,哪家楼层更高呢?为什么?你是怎么知道的?(生讨论发现八楼与九楼都存在于现实空间中,我们可以把这个空间画出来,让数字变得有形)
师:我们在过去运用过这个方法吗?
生:有,我们在直尺上比较数字的大小。
师:那为了方便我们研究刚才的近似数问题,我们可以——
生:画数轴!
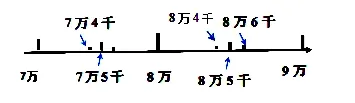
接下来,学生分别尝试拿一些数轴上的数,使用四舍五入的方法,看能否到近似数8万,他们就发现最大的数可以是8万4千,最小的数应该是7万5千。这种类型的题目学生错误很多,分析原因还是由于没找到理想的解题策略——通过画图实现数形结合。通过数轴这一“形”的直观的对应教学,可以让学生直观看到这些数的大小顺序,做到心中有数,不再是凭空猜测,做到有理可说、有据可依。(如图)
美国著名教育心理学家奥苏伯尔曾说:如果要我把所有的教育心理学用一句话概括的话,那就是“教师必须知道儿童已经知道了什么”。笔者认为,教学不能摆花架子,不能为了暂时取悦学生而搞华而不实的课堂游戏,有意义的数学学习就是把客观的知识结构内化为自己头脑中的认知结构,内化需要感受、体验、交流、辨析和有意义的建构,教师要对学生的现实水平有所了解,站在学生已有的起点上,定位目标,不走回头路,不做无用功。让学生充分从事数学探究活动,发挥学生学习的自主性、主动性、选择性和创造性,让学生在自主探索中不断地发展。
