基于车轨耦合模型下地铁对隧土的振动响应

王晓慧，石焕文

(长安大学理学院，陕西 西安 710064)

由于地铁列车本身的动力作用及轨道不平顺，导致车轨之间产生振动，振动通过隧道结构传到地层及周围建筑，诱发室内的二次振动，对人的工作和生活产生不利影响[1]。因此，研究地铁交通引起的振动极其重要。目前研究地铁振动的方法主要有：理论分析、现场测试及数值模拟。ARNAU等[2-4]利用有限元法建立地铁-隧道-土体的三维动力学模型，分析系统的振动响应。郑国琛等[5]建立车轨垂向耦合振动数值分析模型和隧道-土体-建筑物有限元模型，分析建筑物的振动响应。HAMID等[6]建立了移动荷载作用下环境振动的二维预测模型，研究了德黑兰地铁4号线列车引起的环境振动。K.A. K等[7]建立了隧道-土体点荷载沿隧道仰拱运动的相互作用模型，研究了单轨和双轨隧道中铁路运行引起的环境振动。许晨等[8]建立有地裂缝的隧土三维有限元模型，进行模态分析和振动响应分析，并与同工况的无地裂缝结构的振动响应进行对比。目前的研究三维模型计算时结构复杂、耗时长且占用内存大；荷载的模拟大多采用人为假设的激振力，这种计算荷载的方法误差较大。另外，很少有人对隧道壁上高出轨顶1.25 m处的振动开展研究。本文利用 ANSYS 软件建立列车-轨道-隧道-土体系统的二维有限元模型，将该系统模型分为车辆-轨道耦合模型和隧道-土体模型2个子系统[9]，由子系统1得到的竖向轮轨力作为子系统2的外加激励，计算分析隧道道床、地面上点的振动加速度特性，并探讨土体模型的尺寸对地面点的振动影响，所建模型的可靠性通过道床点振动加速度的模拟值和实测值的对比来验证。

1 列车荷载的模拟

基于车辆-轨道耦合动力学理论，利用ANSYS软件建立二维车辆-轨道耦合有限元模型模拟荷载。此模型，车辆采用6节编组地铁B型车，车辆轴重140 kN，车厢、转向架均考虑转动和沉浮运动，轮对考虑沉浮运动，系统共10个自由度[10]；列车悬挂系统用弹簧-阻尼单元模拟，车轮只考虑质量。钢轨和普通整体道床采用有限长度二维Euler梁模拟，短轨枕看作质量块，轮轨用接触弹簧连接；边界条件设定钢轨简支约束，地基底部为全约束。图1是车辆-轨道耦合系统力学模型。

图1 列车-轨道简化模型

根据美国六级轨道高低不平顺密度谱，应用MATLAB模拟得到图2轨道不平顺时间序列，将其作为激励加到钢轨，计算轮轨间竖向作用力。美国六级高低不平顺功率谱密度函数[11]如下：

(1)

其中：Sv(Ω)为轨道高低不平顺功率谱密度；Ω为空间频率；Av为粗糙度常数；Ωc为截断频率；k为系数，当k=0.25时，可使计算值与实测值更为接近。

图2 轨道不平顺时间序列

轨道不平顺时间序列可由以下3步得到：

1)将不平顺单边功率谱密度函数转化为双边谱，得到偶对称序列Sx(f=kΔf)，k=0，1，…，Nr-1。根据周期图法，可获得各频率采样点的频谱模值为

(2)

2)时域序列x(n)为一随机过程，其频谱相位具有随机性。又因复序列X(k)的实部偶对称，虚部奇对称，设ξn是均值为零的独立相位序列，ξn为复数且|ξn|=1，所以只需求出频谱X(k)，k=0，1，…，Nr/2， 即表达式为

k=0，1，…，Nr/2。

(3)

3)将得到的复序列X(k)进行IFFT得到不平顺时间序列

n=0,1,…，Nr-1。

(4)

列车时速为70 km/h，在进行有限元模拟计算时，列车动荷载均匀分布到轨道上的线载荷计算公式如下:

(5)

其中:F(t)为沿轨道均匀分布的线荷载；P(t)为钢轨竖向荷载；N为每节车厢的转向架数(N=2)；n为每个转向架的轮对数(n=2)；L为每节车长(L=19.52 m)；K为分散系数(K=0.9)。计算出图3列车振动均匀分布的线荷载时程曲线。

图3 地铁竖向轮轨力

2 隧道-土体模型的数值模拟

2.1 模型的建立

根据某地铁线路(双线圆形隧道)的地层勘察报告，建立宽度为120 m，深度为75 m的二维隧道-土体模型，将土体从上到下按其性质分为4种不同土层，其高度分别为2.2、4.5、5.3、63.0 m。土体是一种强非线性材料，选取DP本构模型。道床表面至地表面的距离为18 m，左右两隧道中心线距离13 m，隧道外径6.0 m，内径5.4 m，衬砌厚度为0.3 m，表1为隧道内部结构参数。设只有左线列车通过时为单线，选地表面上与轨道左隧中心线距离分别为0、20、23、25、38 m的点研究。表2列出各土层参数。

表1 隧道结构的参数

模型单元尺寸取0.25～1.50 m，越靠近振源处单元网格越密集，越远离振源网格越稀疏，单元尺寸在材料剪切波长的1/12～1/6选取，这样可满足计算精度要求。

在有限元数值分析时，土体只截取其中一部分，振动波在截取的边界面上会发生波的反射，给计算结果带来误差，因此需要设置人工边界以消减误差。即本模型的左右边界采用二维黏弹性人工边界，通过在人工截断边界上设置连续分布的并联弹簧-阻尼器系统，而模型的上表面为自由边界，底边设为固定边界。黏弹性人工边界的弹簧系数KB和阻尼系数CB分别如下式：

表2 土层参数表

其中:KBN、KBT分别为弹簧法向与切向刚度；R为波源至人工边界点的距离；cs和cp分别为s波和p波波速；G为介质剪切模量；ρ为介质质量密度；αT与αN分别为切向与法向黏弹性人工边界参数，二维模型取αT=0.5,αN=1.0。

2.2 道床点的数值模拟结果

图4、图5分别是单双线列车通过时道床上相邻两扣件跨中且到外轨距离0.5 m处测点的数值模拟计算结果。对比两图，单线和双线列车运行引起的道床点的振动规律基本一致，单线振动加速度峰值为0.143 8 m/s2，双线振动峰值为0.338 5 m/s2；单线时道床测点的主要频率在45～85 Hz，双线时的主要频率在40～90 Hz，双线的频率范围比单线更宽。这与文献[12]的结论相同。

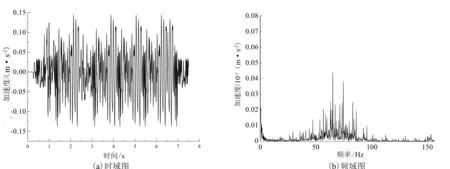
图4 单线车道床的时程图和频域图

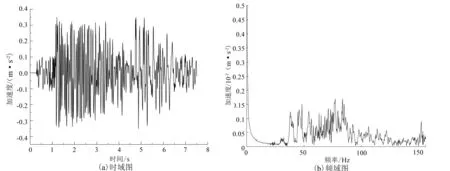
图5 双线车道床的时程图和频域图

2.3 地面点的数值模拟结果

由于单线和双线的振动基本一致，因此列出图6所示双线列车运行时地面点的数值结果，并将单线和双线列车运行时地面点的加速度峰值列于表3。

单双线列车运行时地表面点的振动规律基本一致，在隧道正上方的值最大；双线比单线引起的地面点振动加速度峰值大；振动随着离隧道中心线的距离增加而减弱，在23 m左右出现振动放大区，随后振动衰减缓慢。这与文献[13—14]相符。

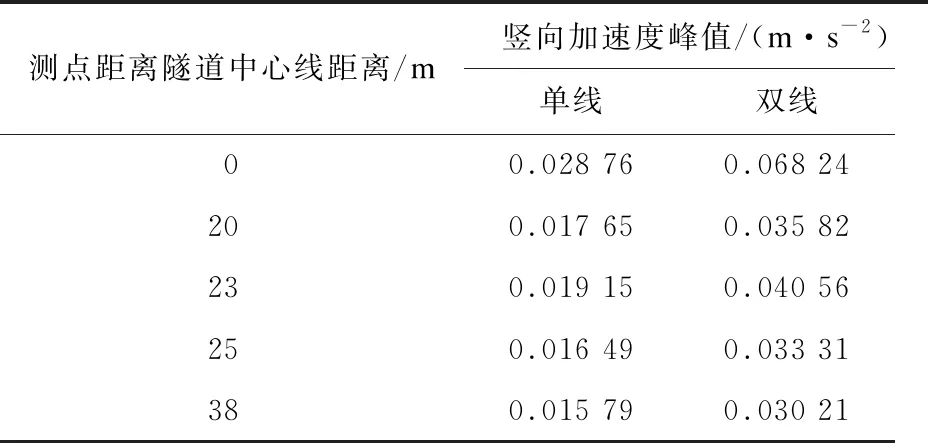
表3 单双线地面点加速度峰值结果

图6 双线列车运行时地面点的加速度时程

2.4 土体模型尺寸的影响

模拟土体时，理论上模型尺寸越大越好，但模型过大不但对精度的提升效果不明显，还会浪费不必要的计算时间，而较小的土体模型尺寸，会影响模型的计算精度，造成误差过大的现象，因此，选择合适的模型尺寸是有限元模拟的基础。建立4种深度、4种宽度的土体模型，且选择地表面左线正上方点的加速度值作为统计结果。分别以最宽150 m、最深95 m的模型计算结果为基准，表4列出其他宽度工况变化、表5列出其他深度工况变化的计算结果与基准模型计算结果的误差。

结果可得，土体模型宽度和深度对地面点的振动峰值影响很大，宽75 m与150 m的模型计算误差为26.35%，深40 m与95 m的模型计算误差为29.51%。随着模型宽度、深度的增加，计算结果误差的变化在逐渐减小，宽120 m与宽150 m模型的误差为3.27%，75 m深与95 m深的模型误差为5.30%。模型宽度、深度要在满足计算精度要求的条件下尽可能大，此二维模型选取120 m宽度和75 m深度的模型尺寸即可。土体模型尺寸的影响结果与文献[15]中结果相近。

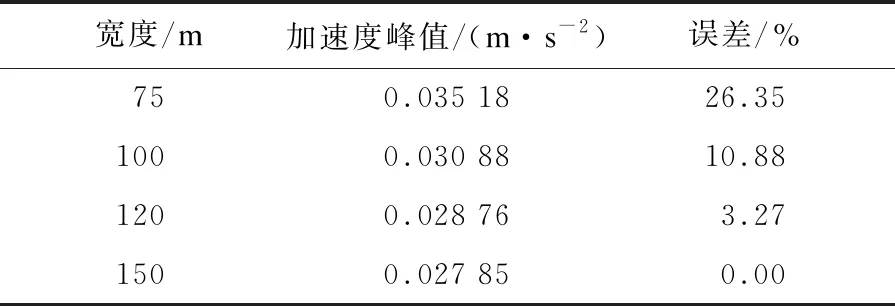
表4 深度75 m时宽度变化的结果和误差

表5 宽度120 m时深度变化的结果和误差

3 道床点振动的实测结果

测试时在道床上布置加速度传感器，测试的采样频率为4 096 Hz，利用采样仪测得地铁通过测点区域时的振动数据。单线即为只左线列车通过，实测点是隧道底部道床上两扣件跨中且距外轨0.5m处。图7、图8为单双线列车通过测点时的振动加速度时域图和频域图。

时程图中，单线列车运行时振动加速度峰值为0.137 2 m/s2，双线加速度峰值为0.320 4 m/s2，即双线列车比单线列车运行时道床测点的振动响应更强；频域图中，单线列车运行时道床上测点振动的主要频率在40～90 Hz，双线列车测点振动的主要频率是35～100 Hz。

图7 实测单双线车通过测点的时域图

图8 实测单双线车通过测点的频域图

实测的各项数值与图4、图5的模拟结果符合较好。

4 结论

本文利用动力有限元数值模拟，结合交通振动的现场实测，对单双线地铁列车运行引起的振动在道床及地面的动力响应进行预测研究。结果表明：

1)通过模拟计算与实测结果对比验证，本文建立的列车-轨道-隧道-土体有限元模型可以有效地预测地铁引起的道床和地面的振动,双线比单线的振动强度大。

2)模拟预测结果可为利用《环境影响评价技术导则城市轨道交通》(HJ 453—2018)预测地面点的最大Z振级公式中振动源强的确定提供参考。地面竖向振动加速度值随着与隧道中心线距离增大而衰减，在23 m左右出现了振动放大区，之后振动响应随距离的增大衰减缓慢。有研究认为这是因为波在软硬不同的土层中重复反射形成的，由此可见，地铁振动不是随着与隧道中心线距离的增加而单调衰减的。

3)二维模型中土体尺寸对计算结果有大的影响，选取模型宽度120 m、深度75 m，即可满足计算精度要求。