融合粗糙集与灰色模型的道岔故障预测

张友鹏，江雪莹，赵斌

融合粗糙集与灰色模型的道岔故障预测

张友鹏，江雪莹，赵斌

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

以高铁常用S700K型转辙机为例，通过预测电流特征实现对未发生故障的预先检修。结合粗糙集与灰色理论提出一种新方法用于道岔故障预测，该方法通过粗糙集的知识获取与规则约简，获得最小诊断规则；通过离散灰色预测模型的建模方法，实时建立不同故障类型的预测模型。随机抽取30组故障进行诊断，其中96.67%与实际情况相符，可满足诊断准确率的要求；随机抽取1组预测情况，预测值与实际值之间的残差较小，可满足预测准确率的要求。所提出方法能够有效减少由故障带来的安全问题，可操作性高，更具实用性。

道岔；故障预测；粗糙集；离散灰色预测模型

道岔是铁路信号设备中最重要同时也是极易发生故障的设备[1]，其安全性和可靠性直接关系铁路的正常运营，因此，对于道岔的故障诊断是十分关键且必要的。经过现场调研发现，道岔故障常常是造成重大事故的主要原因之一，一旦发生故障，即可能造成脱轨、追尾等险性事故[2]。因此，研究道岔故障预测具有重要意义，可在故障发生前，根据预测结果采取针对性措施，确保道岔安全可靠运行。研究表明[3−4]，道岔动作电流可以清晰反映道岔当前所处状态，通过预测，分析道岔动作电流的变化，能得出道岔的变化趋势。近些年，基于Adaboost算法和神经网络等智能技术的故障预测，均取得了一定的成果[5−6]，但由于Adaboost算法迭代次数难以确定且训练时间长；神经网络的收敛速度慢有时还会发散，且需要大量的历史数据，因此，需要寻找一种更为优越的方法。离散灰色模型所需数据少，计算量小、预测精度高，是一种较为理想的预测模型[7]。然而，该模型并不能反映与故障类型的关系，因此，不能单独用于故障预测。研究发现[8−9]，道岔故障类型与其动作电流之间存在很强的对应关系，但通过动作电流获取的数据并不能够很好地满足现有道岔故障诊断方法所需数据量的要求，使得诊断结果的准确率较低，而通过粗糙集知识获取方法，能够在数据量较少的情况下，更加准确地对故障进行分类。因此，提出基于粗糙集与离散灰色模型的道岔故障预测方法，利用粗糙集建立决策表，并对电流特征与故障类型间的规则进行简化；再建立模型对电流特征进行预测，获得预测特征后，对照规则得出最终预测结果。该方法结合预测的动作电流特征和诊断规则，尽早发现还未发生的故障，能预先有针对性地对故障处进行检修。

1 基于粗糙集理论的知识提取与规则约简

粗糙集理论由Pawlak提出[10]，该理论能够有效地对信息进行分析与处理，并从中发现隐含的知识，揭示潜在的规律[11]，尤其适用于数据量较少的故障诊断。

粗糙集理论能有效处理不精确、不一致的信息数据，发现内部潜在关系，得到有用知识[12]，并把研究对象抽象为一个信息系统，在这个信息系统中存在属性与值[13]，而这种属性与值的关系构成一张二维表，称之为决策表。

决策表的生成、化简方法如下：

1) 构建。将选出的电流特征作为条件属性，故障作为决策属性，列出初步决策表。

2) “替换”。将每个数据与其正常状态时的数据进行比较：大于记为2，等于记为1(将属于正常值的±0.1范围内记作等于)，小于记为0。

3) 属性约简。删除多余的条件属性，得到简化决策表。

4) 规则生成。简化决策表的条件属性为规则前件，决策属性为规则后件，生成规则。

2 离散灰色模型的预测原理

离散灰色模型(Discrete Grey Model, DGM)是以微分方程为核心的建模方法，其根据已有信息，通过对初始数据的累加、累减等计算建立模型，利用提供的已知或不确定的数据来计算各参量，并对数据进行预测。

DGM(1,1)的定义形式[14]为：

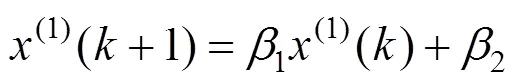
DGM(1,1)建模及预测具体步骤[15]如下：

2) 建立矩阵和，

本文利用DGM(1,1)对道岔动作电流特征进行预测，根据预测结果，结合诊断规则，确定故障类型，为现场道岔故障的预先检修提供依据。

3 基于粗糙集与DGM(1,1)的道岔故障预测方法

利用粗糙集获得最小诊断规则，利用DGM(1,1)获取高精度的道岔动作电流特征的预测值。具体预测过程如图1所示。

图1 具体预测过程

采用直接多步预测，设定某一时刻动作电流特征预测点数目为，通过预测点建模得到预测值，但不宜过大，因为DGM(1,1) 长期预测会出现较大偏差，而短期预测效果好[16]。每一组预测点都反映了道岔动作电流在某一时刻的特征，将特征“替换”后，对照诊断规则，若符合则可知预测的故障类型。

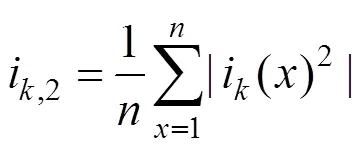
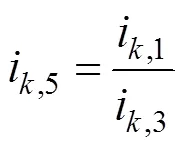
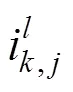
其中：b为类间离散距离，如式(12)所示；w为类内离散距离，如式(13)所示。

根据式(11)~(15)，即可选出最优特征。

选出最优特征之后，进行“替换”。即将特征值用“0，1和2”来替换，“替换”规则为：大于基准值替为2，小于替为0，在基准值正负0.1范围内替为1(基准值选取为道岔正常动作电流曲线的特征值)。

“替换”后，建立决策表，约简得到最小决策表和最小诊断规则。

根据系统已监测到的动作电流数据，计算其特征值，建立DGM(1,1)预测模型(模型中每5个实际值为1组进行预测，预测10次)，并对相应故障类型特征进行预测。截取其中1组预测值，结合“替换”方法，与最小诊断规则的条件属性进行比对，判断符合哪一种，即可得出预测的道岔故障类型。

4 应用实例

本文主要研究高速铁路道岔故障，因此提到转辙机相关故障时，均为S700K型。由于S700K型为交流转辙机，因此对其三相动作电流进行故障预测。根据现场调研可知几种常见的故障如表1所示。

表1 常见故障

以正常动作电流为例，对其进行分区：1DQJ吸起后，曲线开始记录：0−1为启动区；1−2为解锁区，2−3为转换区，3−4为锁闭区；4−5为缓放区，但在其缓放时间内，启动电路中仍会有两相小电流存在；最后1DQJ落下，曲线终止，如图2 所示。

按照图2所示，对其余8种故障类型(2−9)按相应时间区段对电流曲线进行区域划分，提取时域特征参数，利用Fisher准则选出最优特征分别如下。A相：1,7，2,9，3,9，4,9和5,6；B相：1,8，2,9，3,4，4,9和5,2；C相：1,2，2,9，3,9，4,9和5,6。这里做一个简单的解释：A相的1,7就代表A相动作电流曲线在第1个区段内的第9个时域特征参数所对应的值，以此类推，然后通过前文所述的“替换”方法建立决策表，如表2所示。其中，为序号集，为决策属性集，1−15分别为三相动作电流的最优特征所对应的时域特征参数经过“替换”之后得到的状态特征，这些状态特征的集合称为条件属性集。例如：故障8的3，其对应的时域特征参数数值为1.01，经过与正常状态的对比，“替换”为1，即3所对应的值。

分别去掉1−15，对比发现，去掉其中某些条件属性会对诊断结果有影响，根据粗糙集规则简化方法，可得最小诊断规则如表3所示。

从表3可以看出，原来需要15个条件属性得到的决策属性，在经过规则简化之后仅需4个条件属性即可得到，如第8行获取的规则：3(1)∩5(2)∩10(0)∩11(2)Þ(f8)。

由于条件属性的减少，减少了后续故障预测的复杂性。从原有故障数据集中抽取30组进行诊断准确率的验证，结果表明，其中96.67%是符合实际情况的。

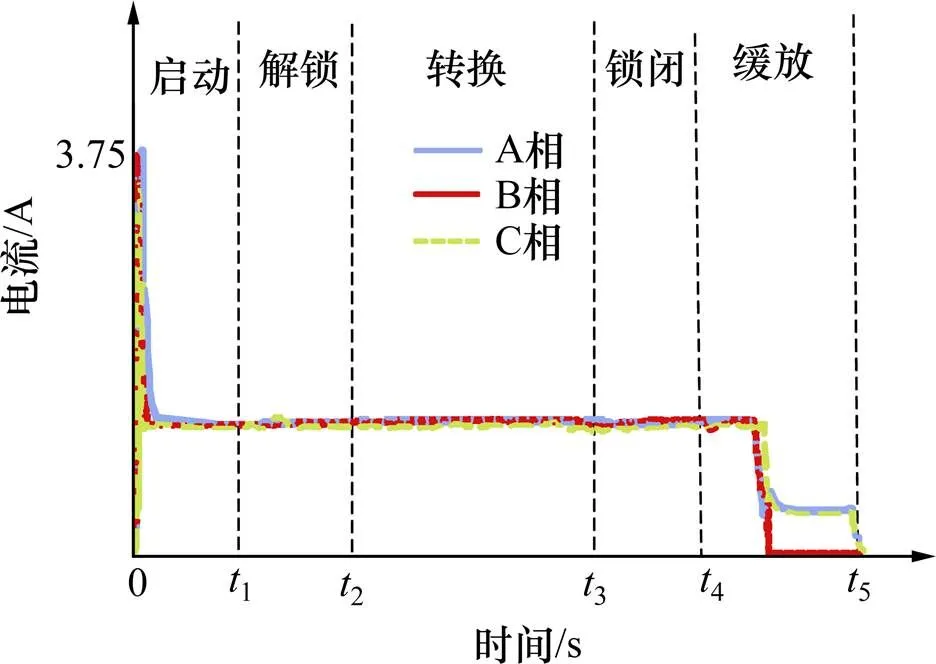
图2 正常(f1)动作电流分区示意

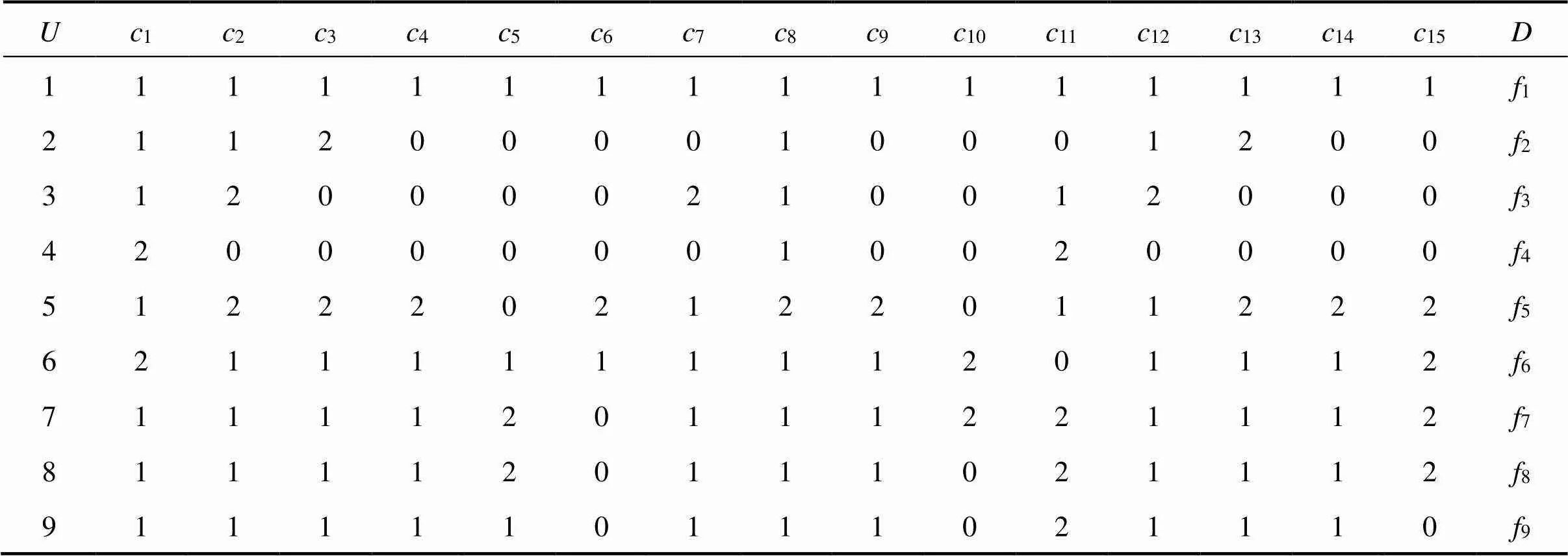
表2 决策表

表3 最小诊断规则

武汉铁路局电务段管辖内，设备名称为1J1的道岔于2015−02−06，12:23:03发生道岔表示整流匣开路故障，取其故障前15次动作的电流数据，将这15次中的第1~5次作为一组初始序列，分别对3，5，10和11建立模型，建立模型分别如式(16)~(19)所示。

3的DGM(1,1)：

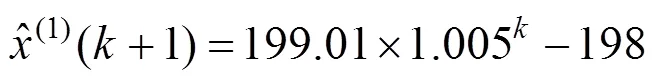
5的DGM(1,1)：

10的DGM(1,1)：

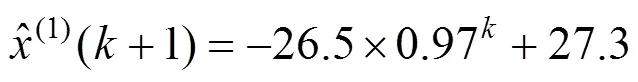
11的DGM(1,1)：

利用式(16)~(19)所建立的模型以及第1~5次的实际动作电流数据所提取的时域特征参数，对后续电流特征参数进行10步预测，得到10次预测的电流特征参数后，对其进行“替换”，然后根据“替换”后的状态特征结合最小诊断规则，得到最后预测的道岔故障类型。

将第1次至第5次的实际值与其相应预测值(这里的预测值其实相当于是模拟值，即根据递推公式以及还原值公式推出来的值)进行对比，并得出残差(模拟误差)，如表4所示。

从表4可以看出，残差(%)均较小，说明预测值与实际值之间的差别较小，满足预测的准确率要求。

根据所建立模型计算预测故障类型的时域特征参数，对其进行“替换”，并最终得出故障预测结果如表5所示，其中预测次数共为10次，即故障发生前的10次道岔动作电流特征的预测，但需要说明的一点是：预测出的并不是准确值，而是接近于准确值的一种趋势。

表4 实际值与预测值对比

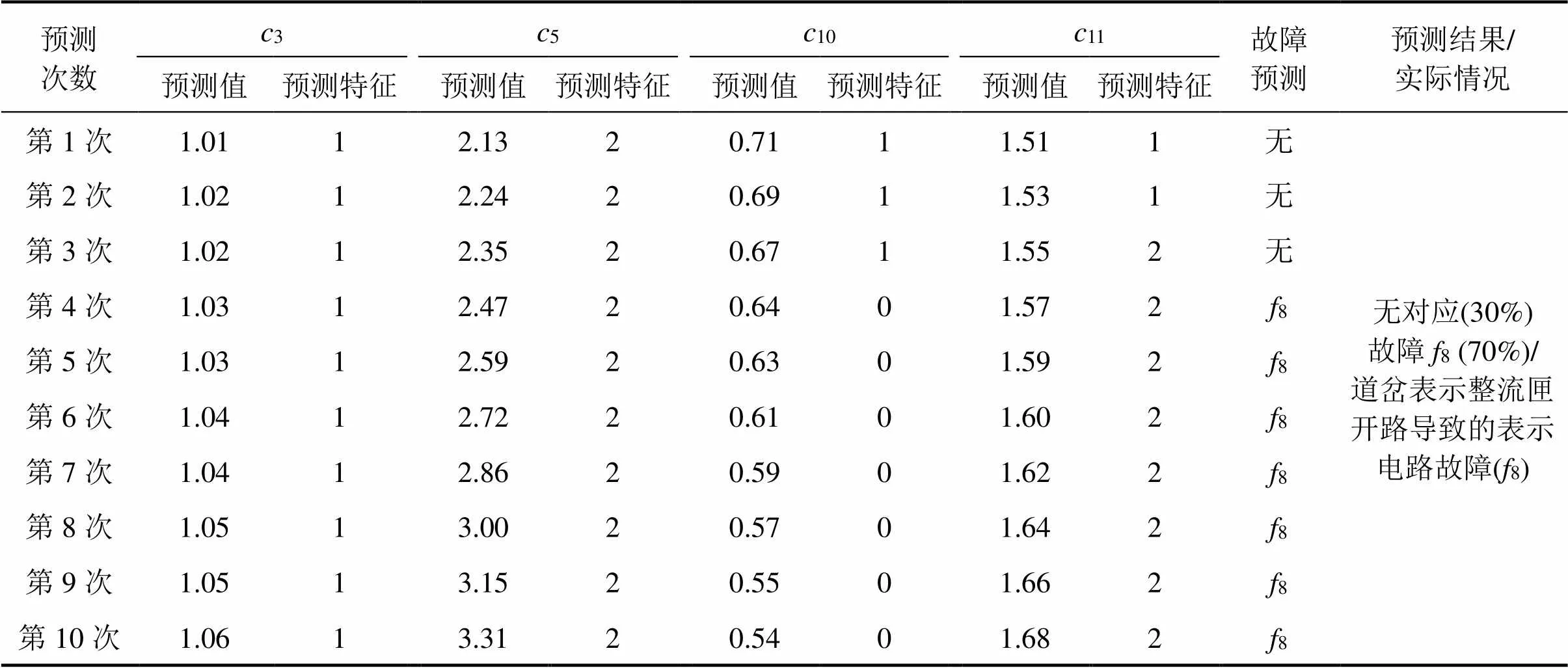
表5 故障预测数据结果

从表5可以看出，第1~3次预测时，故障代码分别为“1211”和“1212”，根据最小诊断规则(表3)可知无此种代码对应的故障类型；当第4~10次动作时，故障代码为“1202”，由表3可知故障类型为8，因而表示电路故障的概率为70%，无对应故障代码概率为30%。

由于无对应故障代码概率低于表示电路故障概率，因此，最终此次预测结果为表示电路故障(未构通)。预测结果与实际情况相符。

若通过早期动作电流特征直接进行故障诊断，则诊断结果为60%正常，40%无对应故障代码，不能正确及时的诊断出故障，如表6所示。这是由于早期电流特征不足以直接准确诊断出道岔的故障，而通过预测则可以获得更多后期可能出现的特征，帮助故障的早期识别。

为进一步验证本文方法的有效性，试验分析了117个实例，其中110例符合实际情况，预测所得故障中，概率最高的特征所对应的故障即为实际发生的故障，预测准确率达到94.02%，而在预测前同时刻基于粗糙集故障诊断方法的准确率仅为17.09%。

据此对比，充分说明，在还未发生故障之时直接利用故障诊断方法是无法有效准确地得出诊断结果，而经过预测后续特征的方法得出可能出现的结果，再对预测结果进行故障诊断能够更为高效、准确的针对还未发生故障的设备进行检修。

部分较为典型的实例如表7所示。对于表7中提出的任一故障，其中实际值特征代码均来自于用于预测的5次实际动作中的最后一次。预测次数为10次。所得故障类型用表1中各故障类型的对应代码表示。

表6 早期故障诊断

表7 实例分析表

从表7可以看出，在早期故障未发生时，利用粗糙集的诊断方法直接对故障进行诊断，准确率是相当低的，原因就在于早期故障特征并不明显，不能准确作出诊断。

5 结论

1) 基于粗糙集的知识获取与规则化简方法，得到用于诊断故障的最小决策表及最小诊断规则，能够更好地反映电流与故障之间的关系，提高了诊断的准确率。

2) 选用的样本是从众多实例中选取的典型案例，因而获取的规则可信度较高。

3) 本文所提方法结合预测电流特征与最小诊断规则，能尽早且准确地发现还未发生的故障，根据预测结果，有针对地对其进行检修，可有效减少故障的发生，避免故障真实发生所带来的安全性问题。

4) 由于电流数据可随道岔动作获得，因此规则库的建立是容易的；又因为预测模型的建立是随数据而变换的，因此是实时建立的，更具实用性。

[1] 林海香, 李阳庆. 面向高速铁路道岔的隐患分析与故障定位改进[J]. 铁道科学与工程学报, 2018, 15(9): 2217−2223. LIN Haixiang, LI Yangqing. Hidden-security-risk analysis and fault location improvement for high-speed railway switch[J]. Journal of Railway Science and Engineering, 2018, 15(9): 2217−2223.

[2] 刘明明, 王良顺, 赵辉, 等. 基于群决策的道岔控制电路故障诊断方法研究[J]. 自动化学报, 2017, 43(5): 1− 10. LIU Mingming, WANG Liangshun, ZHAO Hui, et al. Fault diagnosis method of turnout control circuit based on group decision making[J]. Acta Automatica Sinica, 2017, 43(5): 1−10.

[3] 张星. 基于相似度的道岔故障电流曲线识别方法研究与实现[D]. 兰州: 兰州交通大学, 2016: 10−15. ZHANG Xing. Research and implementation of switch fault current curve recognition method based on similarity[D]. Lanzhou: Lanzhou Jiaotong University, 2016: 10−15.

[4] 王铁军, 董昱, 马彩霞, 等. 基于BP神经网络的道岔智能故障诊断技术[J]. 铁道运营技术, 2011, 17(2): 4−7. WANG Tiejun, DONG Yu, MA Caixia, et al. Fault diagnosis of turnout based on BP neural network[J]. Railway Operation Technology, 2011, 17(2): 4−7.

[5] Yilboga H, Eker O F, Güçlü A, et al. Failure prediction on railway turnouts using time delay neural networks[C]// Computational Intelligence for Measurement Systems and Applications (CIMSA), Taranto: IEEE Xplore, 2010: 1521−1524.

[6] WANG Guang, XU Tianhua, WANG Haifeng, et al. AdaBoost and least square based failure prediction of railway turnouts[C]// 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou: IEEE Xplore, 2016: 2488−2491.

[7] 丁松, 党耀国, 徐宁, 等. 基于时滞效应的多变量离散灰色预测模型[J]. 控制与决策, 2017, 32(11): 1997− 2004. DING Song, DANG Yaoguo, XU Ning, et al. Multi- variable time-delayed discrete grey model[J]. Control and Decision, 2017, 32(11): 1997−2004.

[8] 赵林海, 陆桥. 基于灰关联的道岔故障诊断方法[J]. 铁道学报, 2014, 36(2): 69−74. ZHAO Linhai, LU Qiao. Fault diagnosis method of turnout based on grey relation[J]. Journal of the China Railway Society, 2014, 36(2): 69−74.

[9] 程宇佳. 基于核方法的高速铁路道岔故障诊断方法研究[D]. 北京: 北京交通大学, 2016: 3−9. CHENG Yujia. Research on fault diagnosis method of high-speed railway turnout based on kernel method[D]. Beijing: Beijing Jiaotong University, 2016: 3−9.

[10] 黄文涛, 赵学增, 王伟杰, 等. 基于粗糙集理论的故障诊断决策规则提取方法[J]. 中国电机工程学报, 2003, 23(11): 150−154. HUANG Wentao, ZHAO Xuezeng, WANG Weijie, et al. Fault diagnosis decision rules extraction method based on rough set theory[J]. Journal of Chinese Electrical Engineering, 2003, 23(11): 150−154.

[11] 费胜巍, 孙宇. 融合粗糙集与灰色理论的电力变压器故障预测[J]. 中国电机工程学报, 2008, 28(16): 154− 160. FEI Shengwei, SUN Yu. Fault prediction of power transformer by combination of rough sets and grey theory[J]. Journal of Chinese Electrical Engineering, 2008, 28(16): 154−160.

[12] 张明. 粗糙集理论中的知识获取与约简方法的研究[D].南京: 南京理工大学, 2012: 7−13. ZHANG Ming. Research on knowledge acquisition and reduction in rough set theory[D]. Nanjing: Nanjing University of Science & Technology, 2012: 7−13.

[13] 朱敏玲, 吴海艋, 石磊. 粗糙集规则匹配算法及其在文本分类中的应用[J]. 计算机系统应用, 2018, 27(4): 131−137. ZHU Minling, WU Haimeng, SHI Lei. Rough set rule matching algorithm and its application in text categorization[J]. Computer Systems & Applications, 2018, 27(4): 131−137.

[14] 苏先娜, 谢富纪. DGM(1,1)模型的特性及其在科技创新领域中的应用[J]. 系统工程理论与实践, 2016, 36(3): 635−641. SU Xianna, XIE Fuji. The properties of model DGM(1,1) and its application in technology innovation[J]. Systems Engineering-Theory & Practice, 2016, 36(3): 635−641.

[15] 谢乃明,张可.离散灰色预测模型及其应用[M]. 北京: 科学出版社, 2016: 51−57. XIE Naiming, ZHANG Ke. Discrete grey forecasting model and its application[M]. Beijing: Science Press, 2016: 51−57.

[16] WU Lifeng, WANG Yinao. Modelling DGM(1,1) under the criterion of the minimization of mean absolute percentage error[C]// 2009 Second International Symposium on Knowledge Acquisition and Modeling. Wuhan: IEEE Xplore, 2009: 123−126.

[17] 武汉铁路局电务处. 信号集中监测信息分析指南[M].北京: 中国铁道出版社, 2016: 24−26. Wuhan Railway Bureau Electric Service. Analysis of signal centralized monitoring information[M]. Beijing: China Railway Press, 2016: 24−26.

Turnout fault prediction based on Rough Set and Grey Model

ZHANG Youpeng, JIANG Xueying, ZHAO Bin

(School of Automatic & Electric Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Taking S700K switch machine which is often used in high speed railway as an example, by predicting current characteristics, the fault of turnout which has not happened can be examined and repaired in advance. A new method for fault prediction of turnout based on Rough Set and Grey Theory was presented. And the minimum diagnosis rules were obtained by knowledge acquisition and rule reduction methods which are based on Rough Set. Then through modeling method, discrete grey prediction models of different fault types were established in real time. Thirty groups of faults were randomly selected for diagnosis, and 96.67% of them were consistent with the actual situation, which could meet the requirements of diagnostic accuracy. A group of cases were randomly selected for prediction, and it could be known that the residual between the predictive value and the actual value is small, which could meet the requirement of predictive accuracy. The proposed method can effectively reduce accident rate caused by faults, and also have high operability and practicability.

turnout; fault prediction; Rough Set; Discrete Grey Prediction Models

TP206+.3；U213.6

A

1672 − 7029(2019)09− 2331 − 08

10.19713/j.cnki.43−1423/u.2019.09.027

2018−11−22

中国铁路总公司科技研究开发计划项目(2016J006-A，2015X007-H)；兰州交通大学青年科学基金资助项目(2017052)

张友鹏(1965−)，男，甘肃庆阳人，教授，从事故障诊断及预测研究；E−mail：Jiangxy_105@163.com

(编辑 阳丽霞)