振动荷载与移动荷载作用下桥梁动力响应对比试验与数值分析
2019-03-23彭安平李亮
彭安平,李亮
振动荷载与移动荷载作用下桥梁动力响应对比试验与数值分析
彭安平1, 2,李亮1
(1. 中南大学 土木工程学院,湖南 长沙 410075; 2. 湖南路桥建设集团有限责任公司,湖南 长沙 410075)
依托实际混凝土公路桥梁,分别研究桥面铺装振动压实荷载和成桥试验中的动荷载作用下,桥梁结构的动态响应规律。基于现场测试和有限元计算,确定桥梁模态参数,对比分析桥梁在不同荷载作用下典型的动态响应规律,分别从挠度变形与冲击系数等方面,分析2种荷载对结构安全性和可靠度的影响。研究结果表明:振动压路机工作引起的结构加速度远远大于运营过程中车辆荷载引起的结构加速度,但不会产生可能危及结构安全的较大变形。振动压路机变化的激振力和振动能使结构产生的挠度虽然满足《公路桥涵设计通用规范》的要求,但其对结构造成冲击作用使桥梁结构的计算冲击系数超过其设计值范围。
桥面铺装;跑车试验;动力响应;动挠度;冲击系数

作为交通运输系统中的重要组成成分,桥梁已经成为国家基础设施建设尤其是公路建设中不可或缺的结构形式。在桥梁建成之后,其在桥面铺装施工过程中会受到压路机振动荷载作用,而在运营过程中将受到车辆荷载的作用,这也是桥梁在施工及运营阶段所受到的可能影响结构可靠度和安全性的典型作用。公路桥梁广泛采用沥青混合料作为桥面铺装的主要材料[1],在施工过程中,为了使桥面有良好的平整度,避免沥青层出现车辙等病害[2],需要保证沥青混凝土具有较好的压实度。国内桥面铺装较多采用振动压路机进行碾压施工,在此过程中振动压路机在较高工作频率下产生周期性变化的激振力,该激振力峰值往往超过甚至数倍于压路机本身重量,因此WU等[3]认为桥梁会在压路机的振动频率及激振力作用下出现较大的动力响应,甚至造成结构损伤。目前振动碾压对于桥梁的影响,大多停留在经验和定性分析阶段,少有资料文献对其进行定量分析,邓小斌[4]运用压路机−桥梁耦合振动的分析方法,对高速公路桥梁在不同碾压工况下的加速度响应进行试验研究,发现桥梁在单台振动压路机作用下的最大振动加速度可高达16.62 m/s2。目前人们对于桥梁的健康监测通常是在结构运营阶段进行,将结构在移动荷载作用下的动力响应作为评价桥梁运行安全的重要指标[5]。HE等[6]利用离散小波(DWT)变换分解荷载引起的位移响应变化定位结构潜在损伤,再利用自适应尺度小波有限元模型(WFEM)更新逐步损伤区域的损伤程度。NIE等[7]利用大跨度斜拉桥位移监测数据评估结构的使用性能,发现在桥梁服务10 a后,桥梁预测位移将超过中国规范的设计水平,结构存在潜在风险。ZHONG等[8]通过识别移动荷载作用下结构的动态响应分析桥梁预应力损失。以上研究分别分析了桥梁结构在压路机振动荷载以及车辆移动荷载对结构的影响,仅从单一荷载工况方面评价桥梁结构的安全性,并没有综合对2种条件下桥梁动力响应进行具体的定量对比分析,因此,本文通过对比综合分析桥梁在振动碾压和动荷载试验跑车条件下的挠度、加速度等响应,评价2种荷载对桥梁结构的影响程度。
1 桥面铺装及车辆动荷载现场试验
1.1 工程概况
戴家山大桥是一座湖南省岳阳至望城高速公路中的大型桥梁,全桥为32×30 m连续预应力T梁桥。单幅采用7片主梁,梁高2 m,单片梁宽2.4 m。图1列出了戴家山大桥横截面主要尺寸。
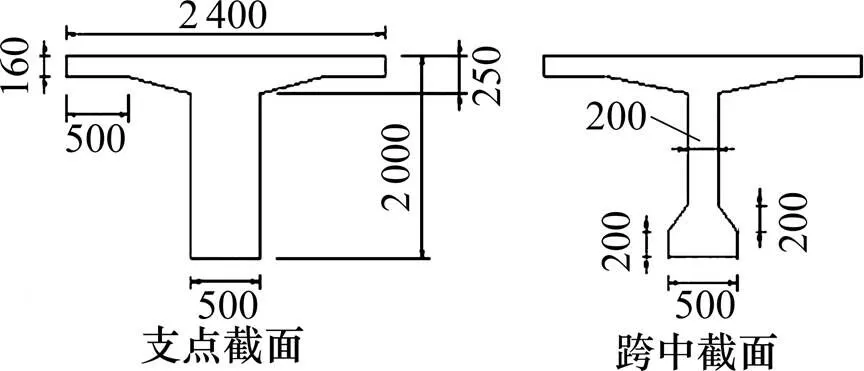
单位:mm
1.2 试验方案
桥梁主梁挠度是桥梁刚度及使用状况的主要监测参数,同时也是桥梁安全性验收及评价的重要指标,依据中国《公路桥涵设计通用规范》[9],钢筋混凝土桥梁结构跨中最大竖向挠度不应超过其计算跨径的1/600。振动加速度是结构振动效应的直观表现,也是表征结构稳定的重要参数[10−11]。动应变是反映桥梁动刚度的物理量[12],对于桥梁动载试验,通常采用结构动应变作为结构动力响应的主要参数。综上,在试验过程中分别测试桥梁在2种荷载作用下的动挠度(应变)和加速度。荷载作用下结构最大动力响应出现在跨中附近,因此2个试验均选择戴家山大桥第2联中跨的跨中进行布点测量,该联为5×30 m连续T梁。
振动碾压试验选择一片边梁进行测试。利用位移计测量跨中动挠度。由于桥梁净空过高,无法直接测量结构挠度,因此将位移计置于测点处悬挂的重物下方以达到接收结构变形目的。加速度采用电压式加速度传感器进行测量,试验方案及测点布置如图2和图3所示。
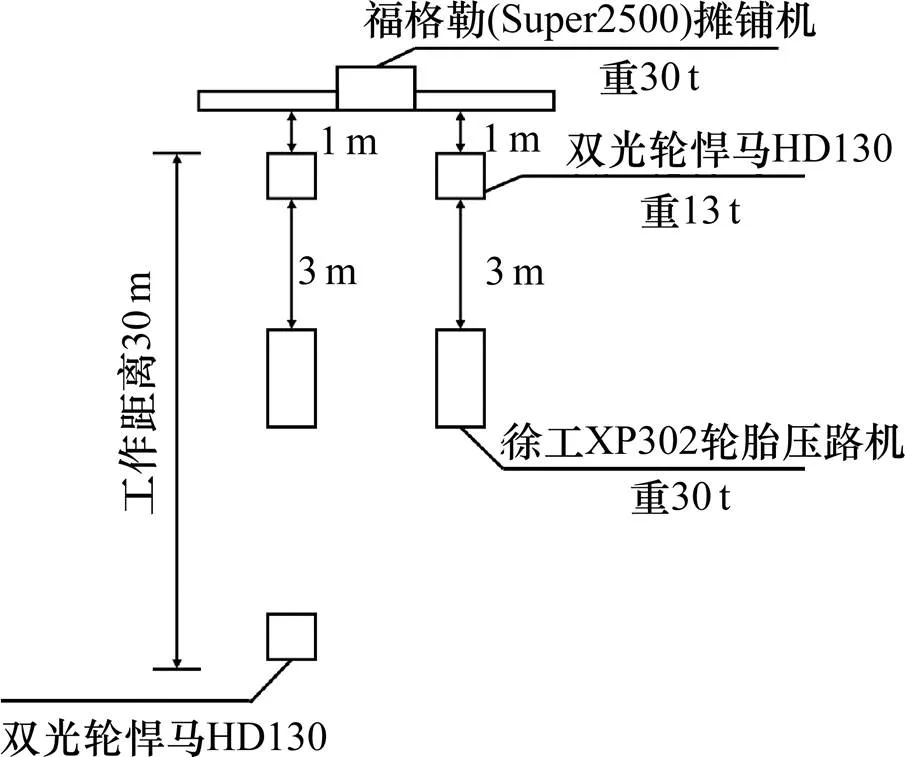
图2 振动碾压试验方案

图3 振动碾压实验测点布置
动载试验主要利用应变片测试中梁在跑车作用下的动应变,并以动应变曲线作为结构在跑车荷载作用下的动力特性指标。桥梁结构本身的自振频率影响结构在荷载作用下动力响应[13],采用加速度传感器收集结构在环境随机激励20 min以上的加速度数据用以计算结构基频。试验过程中,为使加载条件更接近桥梁运营过程中车辆荷载实际车速,使用重型加载车以50 km/h匀速通过试验跨同时采集数据,试验方案及测点布置如图4。

图4 动载试验方案
1.3 试验结果
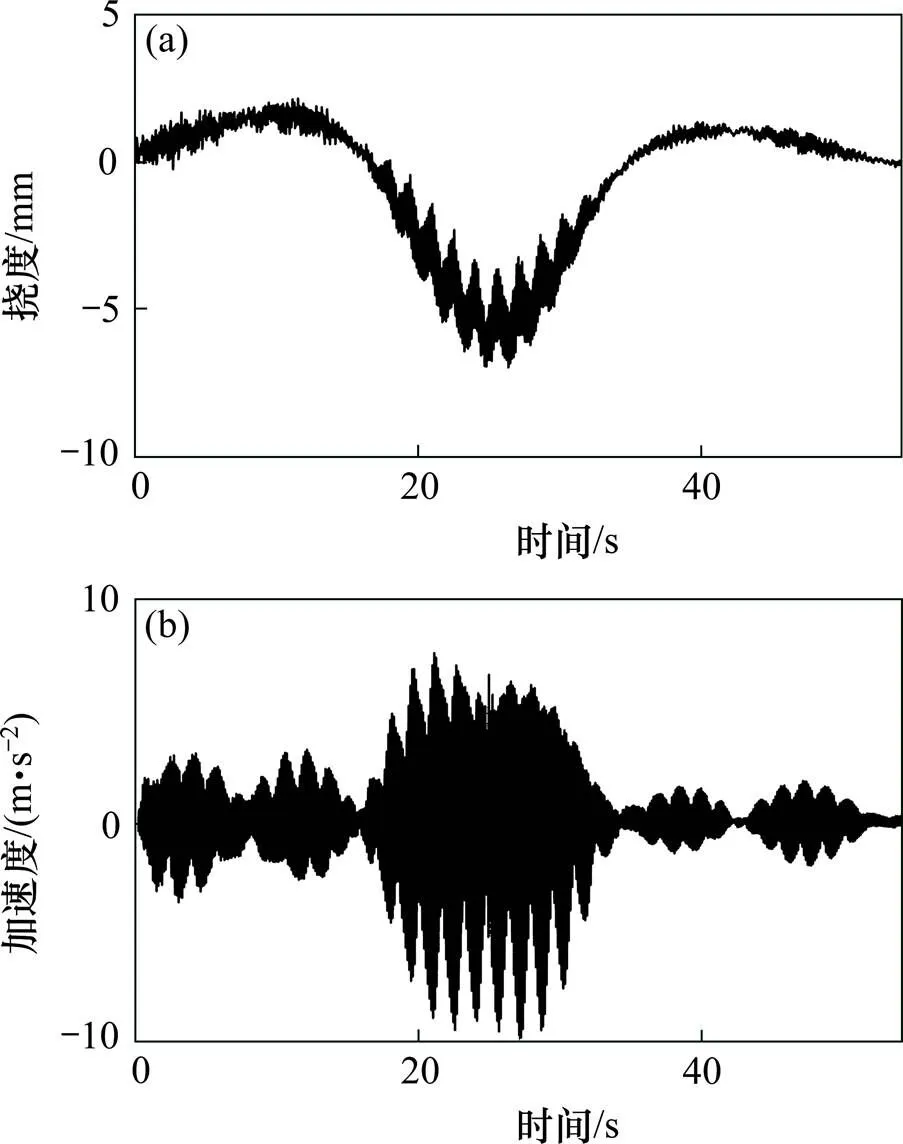
2个试验均采用东华 (DH5922)动态信号分析系统对试验信号进行收集,经过系统内置的滤波器滤波,在振动碾压试验过程中,将42 t摊铺机荷载分别作用于桥梁各个位置,通过有限元计算得到结构在摊铺机作用下的挠度数据,并将实测挠度曲线相应减去摊铺机产生的挠度后得到桥梁结构在振动荷载作用下的挠度、加速度时程曲线以及在动载试验下的动应变时程曲线如图5和图6,可以看出,在压路机振动作用下结构跨中最大竖向挠度为7 mm,加速度最大值为12 m/s2,在跑车试验下,结构最大动应变为31.47 με,加速度最大值为0.34 m/s2,结构在环境随机激励状态下的脉动加速度在±0.02 m/s2之间。对于30 m T梁,《公路桥涵设计通用规范》规定其挠度限值为50 mm,因此2种试验条件下桥梁挠度均未超过规范规定的限值。
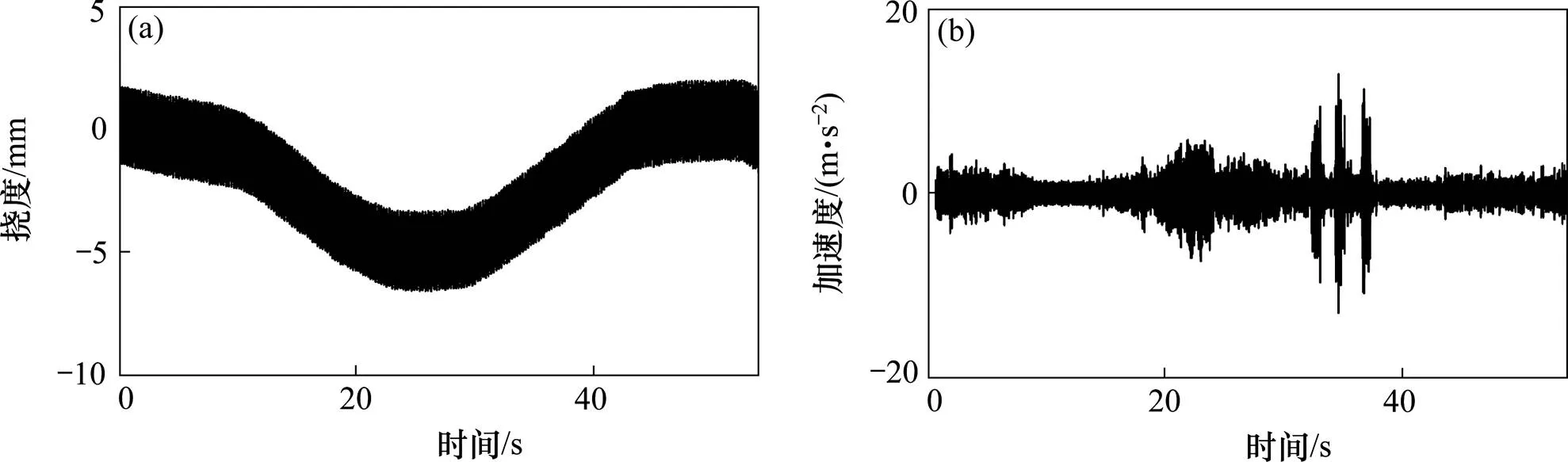
(a) 振动试验实测动挠度;(b) 振动试验实测加速度

(a) 动载试验实测动应变;(b) 动载试验实测加速度;(c) 脉动试验实测加速度
2 振动碾压及动荷载试验数值模拟
由于试验现场桥梁实际荷载较为复杂,除试验荷载外还存在可变作用对现场试验结果产生影响,为探究桥梁结构在2种不同荷载单一作用下的理想响应,分别建立2种试验条件下的有限元数值分析模型,计算对比桥梁动力响应规律。
冲击系数是评价桥梁结构在动力荷载作用下振动效应大小的重要指标[14],定义桥梁在2种荷载行驶过程中跨中产生的最大动挠度(动应变)与相应静荷载直接作用于跨中时跨中产生的最大静挠度(应变)之比为桥梁结构在2种荷载作用下的冲击系数,即:
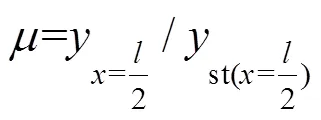
2.1 桥梁结构模型建立
依据表1所列戴家山大桥第2联结构参数,利用ABAQUS有限元软件建立三维有限元模型如图7,实际桥梁上部结构采用C50混凝土,密度为2 700 kg/m3,弹性模量为30 GPa,泊松比为0.35,施加相应的连续支撑条件,采用C3D8R单元类型,共计划分156 000个单元。

表1 戴家山大桥结构参数

图7 戴家山大桥三维有限元模型
2.1 动荷载的施加
双光轮振动压路机在工作过程中通常采用前轮振动的方式,振动轮对桥面作用力大小可看作频率为的简谐力,即:


由于压路机振动轮只能提供压力,因此其对桥面作用力可表示为:

式中:为振动轮重。
前后轮与桥面接触压力由支喜兰等[15]给出的荷载分布公式计算:

式中:为振动轮直径,取1.2 m;为振动轮宽,取2.24 m。
试验选用悍马HD130双光轮振动压路机的工作参数见表2。

表2 振动压路机工作参数
公路桥梁重型轮载一般采用高压轮胎,采用胎压作为接触压力,将轮胎与桥面接触面简化为矩形,矩形尺寸由Yoder等[16]提出的公式进行计算:
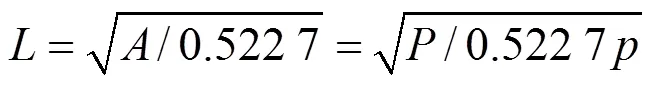
式中:为行车方向接触面长度,m;为轮胎与桥面接触面积,m2;为车辆轮载,kN;为车轮胎压,取0.7 MPa。
动载试验过程中加载车总重=42 t,计算时,将加载车视作前后单轴单轮组轴载,整车质量平均分配至每个轮载,则每个轮载大小=/4=105 kN,则由式(5)计算得到等效后的矩形荷载长度为0.53 m,宽度为0.28 m。其工作参数如表3所示。

表3 动载试验加载车工作参数
2种荷载均通过Fortran语言编写DLOAD用户子程序实现振动、移动荷载的施加。
3 计算结果及对比分析
3.1 模型分析
对有限元模型进行自振频率分析。计算得到戴家山大桥数值模型前4阶振型与频率如图8所示,通过模型分析可知,结构基频为3.725 Hz。
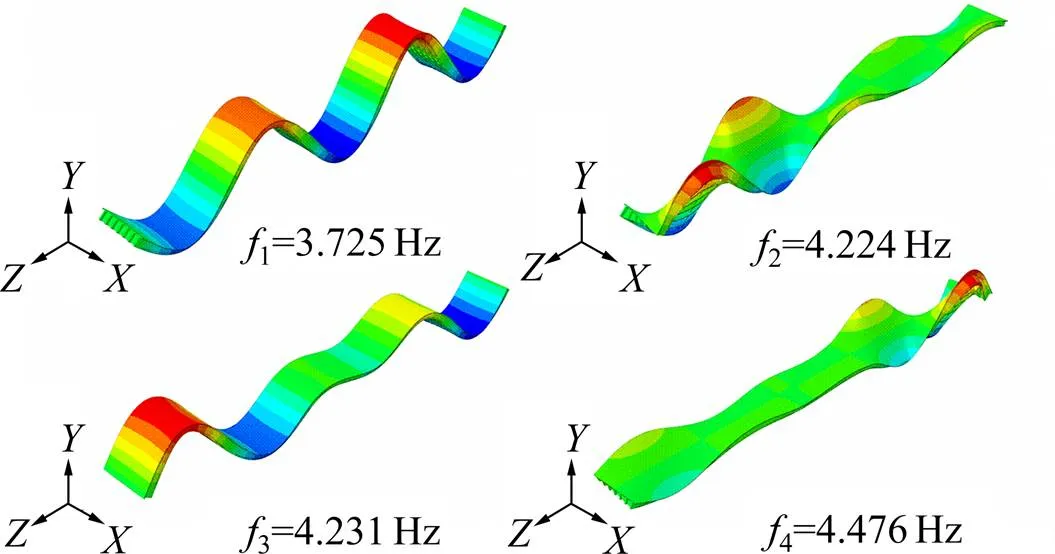
图8 戴家山大桥前4阶振型及频率
依据戴家山大桥现场脉动加速度,利用快速傅里叶变换(FFT)得到加速度平均谱如图9所示,在环境随机激励下戴家山大桥实测自振频率为4.82 Hz,较理论计算得到的结构基频大,说明实际建成桥梁结构刚度较大,结构动力性能良好[17]。

图9 脉动试验自振频谱图
3.2 振动碾压计算结果及对比
利用数值模拟得到桥面铺装振动碾压过程中戴家山大桥跨中挠度及加速度时程曲线如图10所示,并将其与现场实测数据对比如图11。
(a) 振动试验计算动挠度;(b) 振动试验计算加速度

(a) 计算−实测动挠度对比;(b) 计算−实测加速度对比
在压路机振动作用下,桥梁跨中计算最大动挠度均小于50 mm,结构并没有产生危及安全的大变形。桥梁加速度最大值为9.87 m/s2,说明结构在压路机工作过程中会产生较大的振动反应。计算曲线与实测曲线的变化规律和峰值大小基本吻合,这是由于现场施工过程工况复杂,多台轮胎压路机同时工作,因此测点在不同时间内均有不同强度的荷载通过,导致理论与现场实测曲线存在一定差异。

(a) 动载试验计算动应变;(b) 动载试验计算加速度;(c) 动载试验计算动挠度
3.3 动载试验计算结果及对比
通过对跑车试验进行数值计算,得到戴家山大桥在行车荷载作用下的动应变、加速度以及动挠度时程曲线如图12所示。从计算结果可以看出,在加载车以50 km/h通过时,跨中产生的最大动应变为39 με,加速度最大值为0.85 m/s2,跨中最大动挠度为5.17 mm,小于《公路桥涵设计通用规范》规定的最大挠度限制值,结构安全。将数值计算数据与现场动载试验得到的数据进行对比,如图13所示。由于桥梁动载试验工况单一数值计算得到戴家山大桥跑车试验过程中,动应变以及动加速度与现场试验得到的数据吻合较好。

(a) 计算−实测动应变对比;(b) 计算−实测加速度对比
通过对比图可以看出,数值计算结果峰值大与现场实测数据峰值,通过模型频率分析可知,这是由于现场实际桥梁刚度相比于有限元数值模型理论刚度大,因此在荷载作用下桥梁实际动力变形比理论变形及动力响应峰值小。
4 2种荷载作用下桥梁动力响应对比
4.1 挠度对比
将振动碾压以及跑车试验中戴家山大桥跨中计算挠度时程曲线进行对比如图14所示。由于跑车试验下的加载车辆较重,计算得到的跨中最大静挠度为4.12 mm,大于结构在压路机作用下的最大静挠度3.99 mm,但是在压路机作用下跨中动挠度峰值比跑车试验中跨中位置处的动挠度峰值大35%,单位质量压路机产生的动挠度是单位质量加载车产生的动挠度值的2倍。振动作用下跨中挠度幅值为2.07 mm,是跑车试验下结构动挠度幅值的4.16倍,可见压路机振动荷载对结构产生的扰动要大于行车荷载。

(a) 计算动挠度曲线对比;(b) 挠度响应对比
产生以上区别的原因是由于振动压路机作用于桥梁上的激振力时刻变化,相较于车辆移动荷载,压路机激振力产生的振动能量使得结构随之产生较为强烈的振动效应,结构通过较大的垂直摆动消耗压路机的振动能量。
4.2 加速度与冲击系数对比
桥梁振动加速度和荷载冲击系数是结构在动荷载冲击作用下动力响应的重要反映。根据式(1)计算2种试验下桥梁结构的冲击系数,对比绘制柱状图如图15。通过对比可以看到桥梁结构在压路机振动移动荷载作用下,其产生的竖向加速度最大值为9.87 m/s2,而结构在跑车条件下跨中产生的加速度最大值为0.85 m/s2,即振动压路机在桥面铺装施工过程中产生的加速度是在跑车过程中车辆荷载产生的加速度的11.6倍。振动压路机工作过程中对结构产生的冲击系数为桥梁在重型货车作用下产生的冲击系数的1.4倍。这是由于压路机与车辆荷载相比,其振动具有持续性且振动作用力不断改变,使得桥梁在长时间受迫振动的环境内的动力增长效应明显,因而表现出相比于行车荷载作用下更为强烈的振动效应。
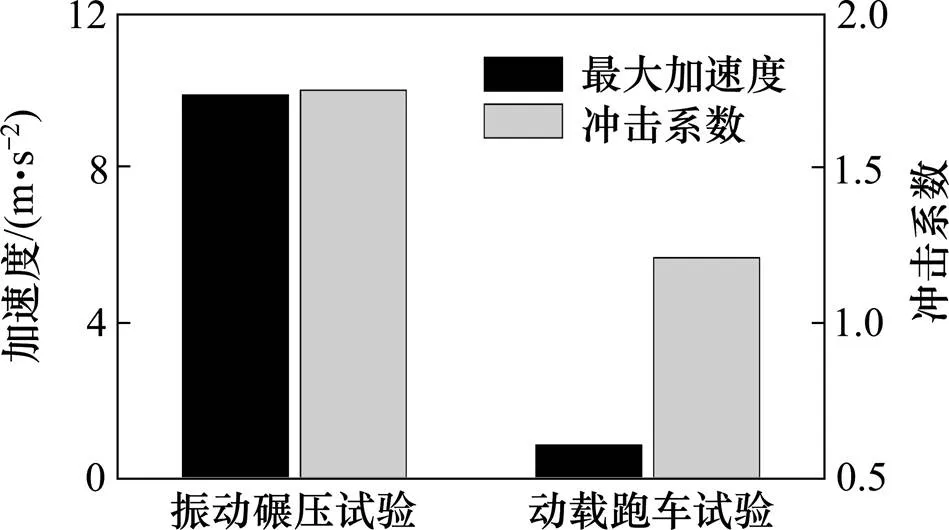
图15 2种试验下冲击系数对比
对于理论基频为f的桥梁结构,《公路桥涵设计通用规范》规定理论冲击系数计算方式如下:
当<1.5 Hz时,=1.005;当1.5 Hz≤≤14 Hz时,=1+0.176 7ln−0.015 7;当>14 Hz时,=1.45。
根据理论计算得到的结构基频得到戴家山大桥理论冲击系数为1.22,与有限元计算跑车试验得到的结构冲击系数1.21接近,因此可以看出行车荷载对于桥梁结构的冲击作用在结构安全范围之内,其对结构的动力影响较小。而振动压路机在桥面铺装振动碾压过程中,对桥梁结构的冲击系数高达1.75,远超过结构的理论冲击系数。
5 结论
1) 分别针对2种工况条件建立对应的桥梁结构有限元数值模型,计算得到桥梁自振特征值与结构的动挠度、加速度及动应变,并与现场试验进行对比验证,两者具有较好的一致性,且实际建成桥梁结构刚度较理论模型刚度大,动力性能良好。
2) 无论是施工过程中振动压路机振动碾压还是日常运营过程中车辆荷载作用,均不会产生可能危及结构安全的较大变形,但是压路机会使结构产生的较大幅度的垂直振动。
3) 振动压路机工作引起的结构加速度远远大于日常运营过程中车辆荷载引起的结构加速度,因此在桥面铺装施工中应适当降低压路机振动频率,进而减小对结构的振动影响。
4) 振动压路机变化的激振力和振动能使结构产生的挠度虽然满足《公路桥涵设计通用规范》的要求,但其对结构造成冲击作用使桥梁结构的计算冲击系数超过其设计值范围。
5) 通过振动碾压过后的荷载试验确定桥梁施工完成后的使用性能和动力性能良好,结构未产生肉眼可见的裂缝,因此施工过程中振动压路机不会造成结构的整体失效,但是其较强的冲击是否对桥梁内部结构造成损伤还需进一步研究。桥面铺装振动碾压过程中,不宜长时间使用振动压路机施工,而是采取静碾与振动碾压相结合的方式,尽快完成桥面压实工作。实际运营过程中,桥梁在车辆荷载作用下仍会产生轻微振动,因此需要关注桥梁结构在常年移动荷载作用下的累计损伤及疲劳问题。
[1] ZHANG K, LUO Y F. Interlaminar performance of waterproof and cohesive materials for concrete bridge deck under specific test conditions[J]. Journal of Materials in Civil Engineering, 2018, 30(8): 04018161.
[2] MA H, ZHANG Z, DING B, et al. Investigation on the adhesive characteristics of engineered cementitious composites (ECC) to steel bridge deck[J]. Construction and Building Materials, 2018, 191: 679−691.
[3] WU S T, HUANG P M, WANG J. Analysis on analogue simulation for oscillatory compaction implementation in bridge deck pavement[J]. Applied Mechanics and Materials, 2014, 488−489: 4.
[4] 邓小斌. 双钢轮压路机在高速公路桥面施工中的应用分析[J]. 交通世界, 2009, 23(12): 80−83. DENG Xiaobin. Application analysis of double steel roller in bridge deck construction[J].Transpoworld, 2009, 23(12): 80−83.
[5] ZHU Xiang, CAO Maosen, Wieslaw stachowicz, et al. Damage identification in bridges by processing dynamic responses to moving loads: Features and evaluation[J]. Sensors, 2019, 19(3): 1−26.
[6] HE W Y, ZHU S, REN W X. Two-phase damage detection of beam structures under moving load using multi-scale wavelet signal processing and wavelet finite element model[J]. Applied Mathematical Modelling, 2018, 66: 728−744.
[7] NIE R F, HUANG Y J, LI S H. In-service condition assessment of long-span bridges based on traffic load effects using monitoring data[J]. Civil Engineering Journal Stavebni Obzor, 2018, 3: 36.
[8] ZHONG H, YANG M J. Prestress loss identification based on dynamic vehicle responses[J]. Journal of Engineering Mechanics, 2018, 144(9): 04018088.
[9] JTG D60—2015, 公路桥涵设计通用规范[S]. JTG D60—2015, General specification for highway bridge and culvert design[S].
[10] XU Y L, LI Q, WU D J, et al. Stress and acceleration analysis of coupled vehicle and long-span bridge systems using the mode superposition method [J]. Engineering Structures, 2010, 32(5): 1356−1368.
[11] 刘汉夫. 铁路桥梁横向振动加速度测试与分析中的技术问题[J]. 世界桥梁, 2005(4): 65−67. LIU Hanfu. Technical issues involved in measurement and analysis of lateral vibration acceleration of railway bridge[j]. World Bridge, 2005(4): 65−67.
[12] 周洁. 某钢管混凝土系杆拱桥静动载试验研究[J].城市道桥与防洪, 2019(1): 79−83, 13. ZHOU Jie. Study on static and dynamic load test of concrete filled steel tube bowstring arch bridge[J].Urban Roads Bridges & Flood Control, 2019(1): 79−83, 13.
[13] Ticona Melo L R, Bittencourt T N, Ribeiro D, et al. Dynamic response of a railway bridge to heavy axle-load trains considering vehicle–bridge interaction[J]. International Journal of Structural Stability and Dynamics, 2017: 1850010.
[14] 郭钰. 高墩连续刚构桥车辆—桥梁冲击系数分析及改善措施[D]. 银川: 宁夏大学, 2017. GUO Yu. Analysis and preventive measures of impact coefficient of high-pier continuous rigid frame bridge[D]. Yinchuan: Ningxia University, 2017.
[15] 支喜兰, 江晓霞, 沙爱民. 路面基层振动压实作用下的底基层应力[J]. 长安大学学报(自然科学版), 2003, 23(3): 33−36. ZHI Xilan, JIANG Xiaoxia, SHA Aimin. Pavement subbase course stress by vibrating compaction on course[J]. Journal of Chang’an University (Natural Science Edition), 2003, 23(3): 33−36.
[16] Yoder E J, Witczak M W. Principles of pavement design [M]. 2nd Edition, 1975.
[17] 陈晓明. 一般桥梁结构动力性能数据分析研究[J]. 北方交通, 2018(7): 76−78. CHEN Xiaoming. Research on data analysis on dynamic performance of ordinary bridge structure[J].Northern Communications, 2018(7): 76−78.
Comparative test and numerical simulation of dynamic response of bridge under vibration load and vehicle load
PENG Anping1, 2, LI Liang1
(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Hunan Road & Bridge Construction Group Co., Ltd, Changsha 410075, China)
Based on the actual concrete highway bridge, this paper studies the dynamic response laws of the bridge structure under the compaction load during the process of bridge deck pavement vibration compaction and the dynamic load in the bridge test. Based on field test and finite element modeling analysis, this paper determined the structural modal parameters, compared the typical dynamic response laws of the bridge under different loads,and analyzed the effects of above two loads on the safety and reliability of the structure from the aspects of deflection and impact coefficient. The research results show that the structural acceleration caused by the vibratory roller is far greater than the acceleration caused by the vehicle loads during the operation, but there is no large deformation that may endanger the structural safety. The vibrational force and vibration energy of the vibratory roller can make the deflection of the structure meet the requirement of the “General specification for design of highway bridges and culverts”, but it will make the calculated impact coefficient of the bridge exceed its design value range at the same time.
bridge deck pavement; dynamic load test; dynamic response; dynamic deflection; impact coefficient
U448.213.333
A
1672 − 7029(2019)09− 2256 − 09
10.19713/j.cnki.43−1423/u.2019.09.017
2018−11−02
湖南省交通科技项目(201622);国家自然科学基金资助项目(51308554)
彭安平(1972−),男,湖南邵阳人,高级工程师,博士研究生,从事道路与桥梁工程方向的研究;E−mail:663357762@qq.com
(编辑 涂鹏)
