微型桩-锚索联合支护顺层岩质边坡的稳定性分析

姜华

微型桩-锚索联合支护顺层岩质边坡的稳定性分析

姜华

(湖南省交通科学研究院有限公司，湖南 长沙 410005)

以衡邵高速公路K128顺层边坡为依托，根据项目特点及支护方案，结合层理节理概率分布模式以及层面软化特性，利用UDEC数值软件建立基于离散单元法的顺层岩质边坡的数值模型，进行不同工况下支护与非支护方案的稳定性分析及支护结构受力分析。数值模拟结果与实际现场情况吻合良好，所建立的数值模型能够综合反映结构面强度、岩层厚度、岩层倾角等关键因素对顺层岩质边坡破坏失稳模式的影响。基于该离散单元法数值模型，对提出的微型桩-锚索联合支护方案进行支护效应分析。采用微型桩+锚索联合支护后边坡的安全系数得到显著提高，边坡的潜在失稳模式由中层的沿软弱层面滑动转变为浅层坡体圆弧型滑动。微型桩和锚索支护的结果内力均处于设计安全范围之内，且能保留较大安全储备。

顺层；边坡；微型桩；离散单元法；数值模拟

随着国内交通基础设施的建设，在公路铁路等工程领域出现了大量的岩质工程边坡，其中顺层岩质路堑边坡出现失稳的情况尤为突出。顺层岩质边坡是指路堑边坡倾斜方向与岩层的倾向接近或大体一致的边坡。顺层岩质边坡的稳定性受到地层岩性、地质构造、地形地貌、水文地质特征及路堑开挖形式等影响。较多研究人员对顺层岩质边坡失稳机理进行了研究。高永涛等[1−2]对岩质边坡的变形破坏模式进行了划分。白松松等[3−4]也通过模型试验研究了顺层边坡的变形模式和破坏机制。李安洪等[5−6]总结提出顺层岩质路堑边坡的分类及8种顺层边坡破坏模式，尤其是结构面强度、岩层厚度、岩层倾角等因素对边坡稳定性的影响最为剧烈[7]。成永刚等[8−9]通过数值模型研究了顺层滑坡实例在初始设计状况下全断面开挖后无工程防护时的坡体状态，以及变更设计后工程防护对坡体的加固效果。杜衍庆等[10−11]报告了微型桩和斜拉锚杆复合结构来治理路堑滑坡的实际案例。衡阳至邵阳高速公路是连接湖南省2个重要地级城市衡阳市和邵阳市的主要交通通道。依托边坡工程位于衡邵高速K128+800~K128+880右侧，长约944 m，最大切深38m，该路堑区属丘陵地貌，相对高差约40 m。自然坡度8.53°~15.64°，局部地区坡度较陡。岩层倾角与边坡倾角一致为顺层岩质边坡。2015年5月上旬，因持续降雨导致此段路堑边坡出现滑坡，滑体堆积于边坡及右幅路面上。滑坡后缘已经明显拉裂错开，张拉裂缝最大深度超过10 m，由于滑坡形成的后缘成直立状，近临裂缝的通讯塔处于不安全状态。常规边坡的稳定性分析计算方法无法有效考虑结构面强度、岩层厚度、岩层倾角等关键影响因素对边坡稳定性的影响。而离散单元法对顺层岩质滑坡具有良好的解决方案。因此本文针对依托工程进行了较完整的离散单元数值模拟分析。目前，边坡在按相关方案支护后处于稳定状态，说明支护设计方案可靠，数值模型合理。从而为类似路堑边坡可能出现的顺层滑坡治理提供设计思路和工程参考价值。

1 边坡工程概况

1.1 地质概况

根据现场调查、钻孔资料、切方路基资料，滑坡区主要地层岩性如下：1) 黏土，褐黄色，稍湿，见少量黑色团装和碎石，硬塑状，局部见灰岩出露，整体厚度不大，约0~3 m；2) 强风化泥质灰岩：灰黄色，隐晶质结构，中厚层状构造，岩石呈碎块状，部分已风化成土状。一般厚度在2~3 m；3) 中风化泥质灰岩与泥灰岩互层：深灰色，隐晶质结构，中厚层状构造，层厚80~120 cm，岩芯呈柱状，与灰黑色薄层状泥灰岩呈互层状，层状泥灰岩层厚10~20 cm，其中薄层状泥灰岩水稳定性差，易风化剥蚀。该区段地表水主要表现为地表汇水，地下水类型则主要为第四系松散堆积层中的潜水和基岩中的裂隙水，其补给来源以大气降水为主。路堑边坡大部分为中风化泥质灰岩与泥灰岩互层，其产状为140°~150°∠25°~30°，坡向与岩层倾向呈65°夹角左右。对应路线横断面方向为倾角约11.7°顺层坡，且坡面局部段落竖向节理发育，岩体切割强烈，对边坡稳定性极为不利，边坡全貌及地质剖面图如图1所示。

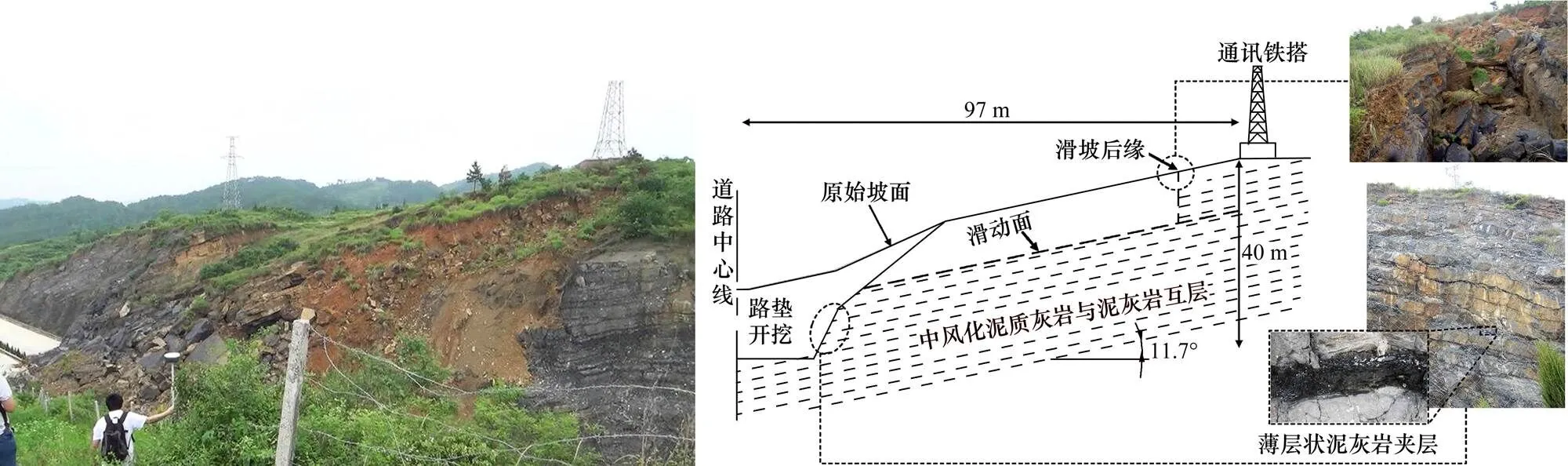
图1 路堑边坡全貌及地质剖面图

1.2 滑坡原因及其类型分析

根据地勘报告和现场分析，该段路堑滑坡成因如下：1) 该边坡右侧岩体产状为倾向于路基方向的顺层坡且层理面在坡面出露，对边坡稳定极为不利；2) 边坡岩体以泥质灰岩与泥灰岩互层为主，倾角40°，纵向间距4 m薄层状泥灰岩水稳定性差，遇水易膨胀软化，层面光滑，质地软弱；3) 连日持续降雨，导致大量雨水通过竖向节理和裂隙下渗至该边坡的软弱夹层，进一步降低了层面抗剪强度，加剧了边坡的失稳变形。该边坡为典型顺层岩质滑坡，滑动面为沿着岩层倾向的直线滑动。由于滑坡后缘张拉裂缝宽度达数米，深度超过10 m，导致该滑坡以上山体长时间临空状态，危及到附近移动通讯塔的安全。

2 顺层岩质边坡离散单元法数值模型

2.1 离散单元法

天然岩体所具有的节理或层理表现出显著的不连续性，极大地限制了连续连续介质方法在层状坡体稳定性分析中的应用，非连续介质力学的方法由此得到发展和应用。比如采用块体离散单元法，可以将岩体假设为一系列完全刚性或者可变形的块体集合，通过定义块体之间的力学接触行为来模拟其集合体的受力、运动及变形等过程[12]。

图2 离散单元法块体与接触及计算循环

UDEC是一款处理二维岩石力学问题的离散单元法程序。其将接触(节理或层理面)视为连续体(岩块)的边界。块体界面的接触力及位移通过对相邻块体运动方程求解获得，块体在其界面处能够相互滑动或脱离[13]。UDEC通过有限时步迭代算法不断循环计算，直至得到的平衡状态的解。计算过程的每一步包含2个基本部分(如图2所示)。每一计算步首先更新接触行为和块体位置的信息，然后对接触应用接触本构关系求解力与位移，从而得到块体间的接触力。根据接触力应用牛顿第二定律求解每个块体的运动，块体可以进一步划分为更小的变形单元，根据单元本构关系求解块体变形[14]。

天然岩体可以视为通过接触黏结在一起的大量可变形岩块的集合，岩体内不同层理节理可以通过赋予层理或节理界面的接触参数进行定义。岩块的变形特性通过弹性模量及泊松比表征。而块体间接触的变形特性通过接触的法向刚度n及切向刚度s进行表征，接触的强度则通过接触的摩擦角j、黏聚力及抗拉强度来定义。当块体间接触力在接触强度以内时，模型通过块体变形模量和接触刚度产生变形；而当接触力超过接触强度时，接触破坏，相邻块体发生滑移或者脱离，接触丧失抗拉强度及黏聚力[15−17]。

2.2 模型参数及反分析结果

对于依托工程的顺层岩质滑坡来说，在确定了滑动方式的前提下，要对其进行合理地稳定性分析以及后续加固方案模拟，需要明确2个问题：1) 层理和节理的分布及模拟；2) 层理节理的岩体力学参数取值，特别是软弱夹层的抗剪强度参数。天然岩体的不连续面空间分布特征，比如节理层理面的倾角间距连通性等均非常数，且有着强烈的随机性。为了更合理地模拟层理节理，根据现场勘查揭示的数据将节理及层理面的倾角和间距2个关键参数视为服从正态分布。其中层理面倾角均为11.7°，层理面间距概率密度服从平均值为1.2 m标准差为0.2 m的正态分布，竖向张拉节理间距服从平均值为1.5 m标准差为0.5 m的正态分布，竖向张拉节理倾角服从平均值为90°标准差为10°的正态分布。分布模式如图3所示。

工程上常用岩石软化系数来表征岩石遇水发生强度降低的特性，指水饱和状态下的岩石试件与天然含水状态下试件单向抗压强度之比，它是判定岩石耐风化、耐水浸能力的指标之一。边坡岩体中薄层状泥灰岩含有较多亲水矿物，其具有遇水膨胀、软化、崩解和失水收缩、开裂的特性，通常泥灰岩软化系数一般在0.5~0.8之间，并随着浸水时间变化而变化，因此坡体层理内泥灰岩强度参数实际分布并不均匀，大致规律为从坡体深部往表面强度逐步降低。因为越靠近坡体表面岩石节理越发育，雨水入渗对泥灰岩强度降低影响越大。因此假定在数值模型中泥灰岩软化系数沿埋深线性增加，地表处软化系数最低取0.5(完全软化)，40 m埋深软化系数为1.0(无软化)。层理面抗剪强度则按照软化系数进行相应折减。

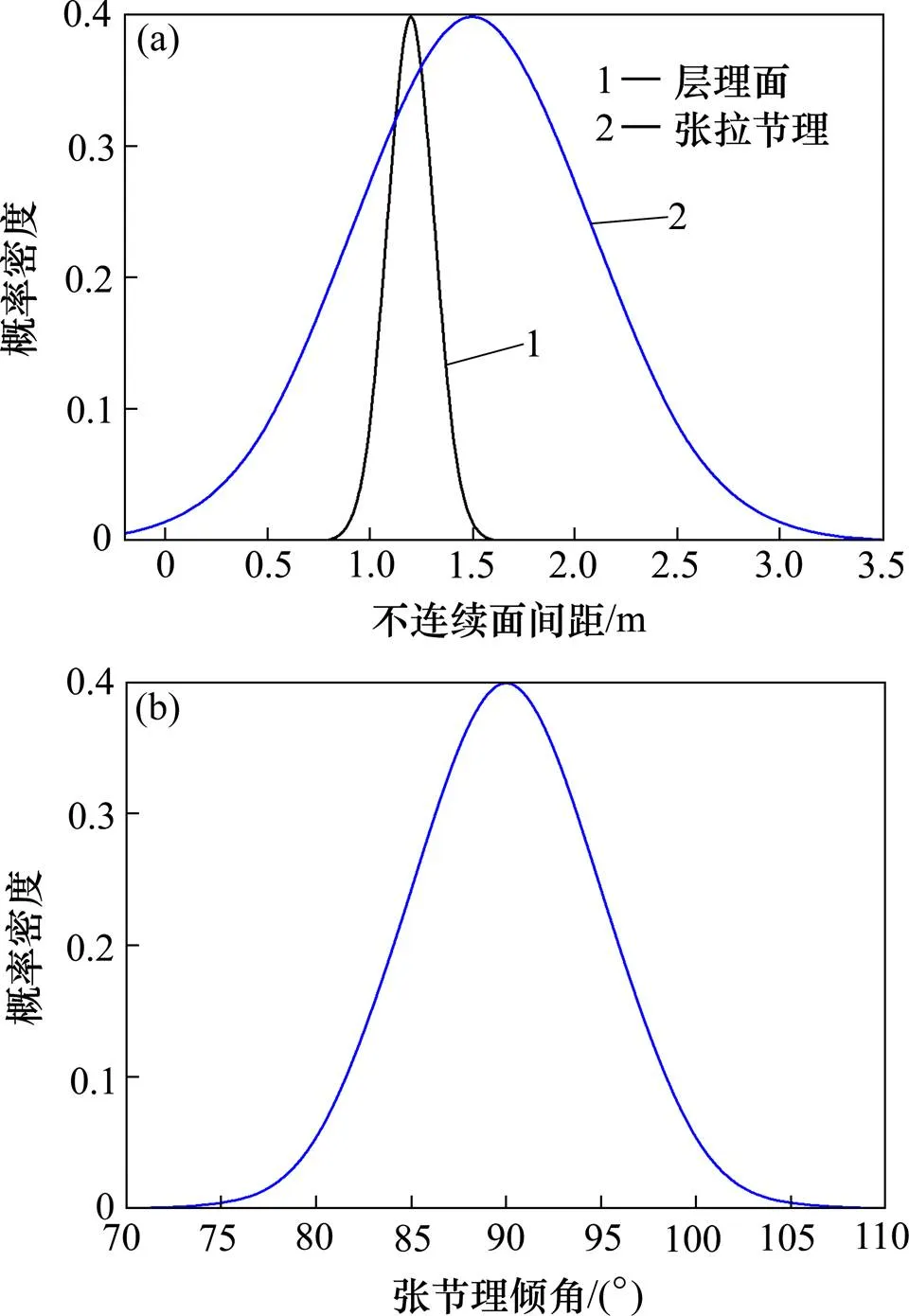
图3 层理节理关键参数概率分布

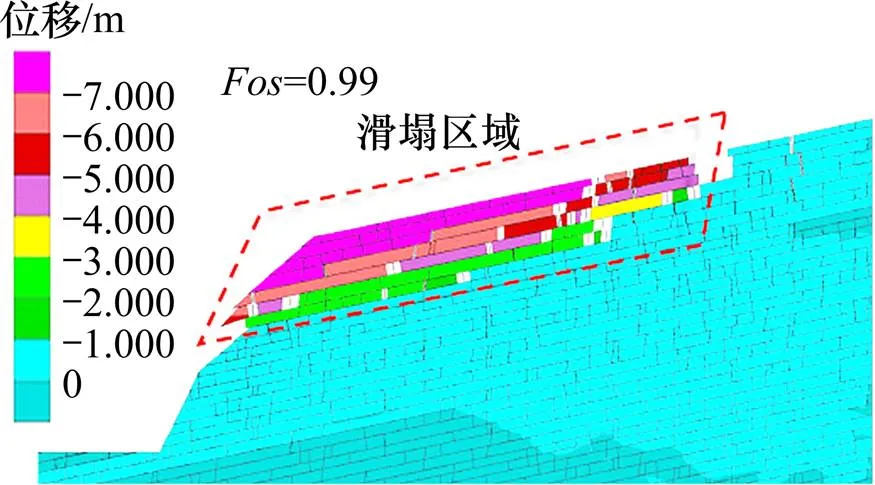
图4 原始边坡失稳模式及安全系数

在确定了层理面抗剪强度分布模式后，层理面的抗剪切度参数取值就决定了边坡数值模型的失稳方式，其具体数值应当在试验及经验参数的基础上结合数值模拟反分析获得。因此假定目前边坡状态为临界失稳状态，安全系数略小于1.0。在确定其他参数按照试验及经验结果选取后，通过调整层理面抗剪强度，计算不同强度参数下对应的安全系数以及对比数值模型及现场坡体失稳形态，确定合理的层理面参数。最终采用强度折减法求解边坡数值模型安全系数，计算值为0.99，坡体失稳形态见图4，与现场较为一致，由此确定相应的数值模型参数，如表1所示。

表1 坡体数值模型参数

3 滑坡加固设计方案

针对该段边坡滑坡失稳方式和目前垮塌区域，采用基本处治思路为“破裂区域刷方卸载，预应力锚索整体加固，微型桩提高浅层中层抗剪强度，浅层锚杆加固，保护坡面加强坡面排水”。具体方案如下：1) 清除坡体已经滑塌部位，对边坡进行刷方卸载。2)一级边坡设置两道预应力锚索地梁，倾角30°，纵向间距5 m，采用7S15.2 mm预应力锚索，预应力600 kN。3) 2级平台布置微型桩接挡墙加固，挡墙材料M10浆砌片石，顶宽2.0 m，底宽2.6 m，墙高2.0 m，基础埋入地面之下1.0 m；挡墙上布置一排预应力锚索，倾角30°，纵向间距5 m，采用7S15.2mm锚索，预应力300 kN；挡墙底部布置150 mm微型桩，桩距1.25 m，梅花形布置。4) 3级平台布置微型桩接挡墙加固，挡墙材料M10浆砌片石，顶宽2.0 m，底宽3.0 m，墙高4.0 m，基础埋入地面之下2.0 m；挡墙布置两排预应力锚索，倾角30°，纵向间距5 m，采用4S15.2 mm预应力锚索，预应力300 kN；挡墙底部布置150 mm微型桩，桩距1.25 m，梅花形布置。5) 2，3和4级坡面浅层岩体采用28 mm全长黏结锚杆加固(长度9 m和6 m间隔布置)，倾角40°，纵向间距4 m，坡面高度方向间距2.50 m，整个坡面5 cm厚喷砼(内置钢筋网)进行封水处理。

4 加固方案数值模拟分析

根据滑坡加固设计方案建立数值模型，如图5所示。其中锚索、锚杆及微型桩均采用线性结构单元进行模拟。结构单元由2个节点构成，可以承受轴向力，并能模拟在拉压条件下杆体材料的屈服，一根支护结构由多段结构单元组合而成。锚索及锚杆不能抗弯，桩单元能够抗弯，三者都能考虑单元与岩体之间的黏结锚固效应。进行清方后按设计坡率开挖的边坡在无支护结构情况下的稳定性分析见图6所示。在无支护条件下坡体仍处于临界破坏状态，根据位移分布图揭示存在浅部和深部2个沿层面的潜在滑动面，根据速度场和强度折减法计算结构揭示其中最危险的潜在滑动面为浅层，安全系数仅有1.02，深层安全系数稍高为1.1。在坡体顶部出现了较大范围的张拉裂缝发育区，如果不采取有效支护，随着雨水进一步入渗软化层面强度，边坡随时有可能发生进一步滑塌。

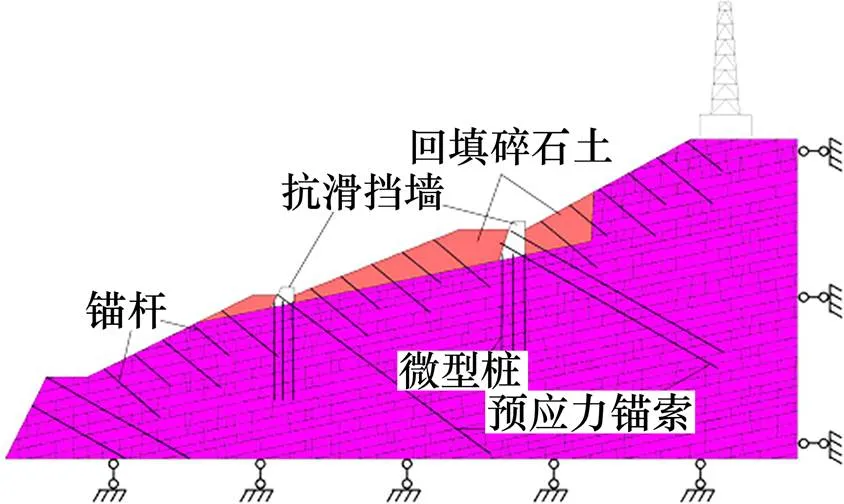
图5 边坡支护数值模型及边界条件

清方后坡体在设计支护结构下的位移场速度场分布见图7。从位移分布来看，在支护结构的作用下坡体位移得到了显著的限制，相比支护前位移可忽略。从速度场来看，在支护结构的联合作用下坡体的潜在失稳方式也发生了改变，从浅层中层的沿软弱层面滑动变成了2级和4级坡体浅层近圆弧型滑动。间接说明了微型桩+锚索联合支护产生的效果，有效阻止了连续层面滑动趋势的形成，从而提高了坡体稳定性及安全系数。采用强度折减法进行稳定性分析揭示支护后坡体潜在滑动面则为第四级坡体浅层圆弧滑动面，安全系数为1.35(图7)。坡体顶部仍有张拉裂缝发育区，但范围和深度较无支护工况明显减小。未支护工况下潜在层间滑动面安全系数均大于1.35。

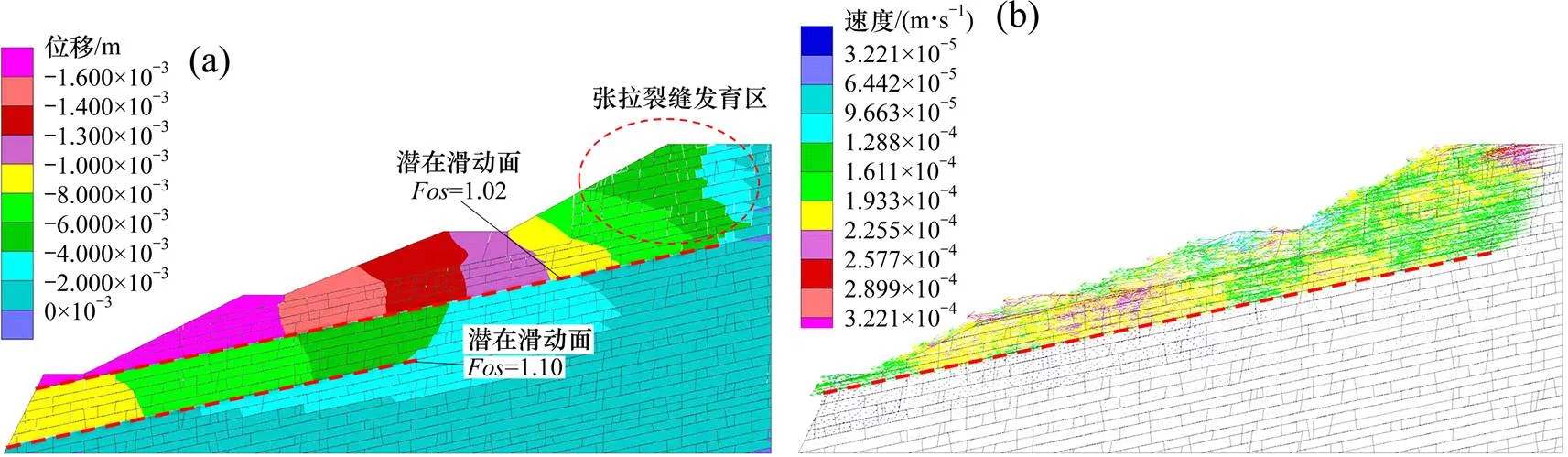
图6 按设计坡率清方后未支护边坡位移场、速度场及失稳模式

图7 按设计支护加固后边坡位移场及速度场

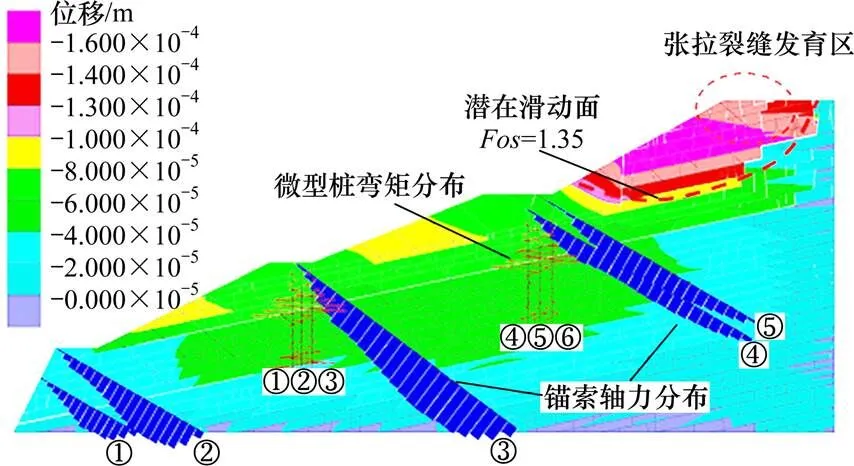
图8 按设计支护加固后边坡失稳模式及支护结构内力

在坡体强度按安全系数1.35折减基础上进一步进行支护结构的内力计算，计算结构见图8，其中锚索内力显示为单元轴向拉力，微型桩内力则为桩体弯矩。具体每根锚索及微型桩的内力分布见图9所示。

由于施加预应力后，坡体会有一定程度压缩，因此每根锚索在浅部轴力均有一定程度损失。沿着锚索长度到锚索中部轴力逐渐恢复接近设计的预拉力。其中3号锚索最大轴力超过600 kN预拉力，说明坡体中部仍有一定程度下滑变形从而再次张拉锚索引起轴力增加。但坡体上部及下部变形较小，各锚索轴力均在安全范围之类，且保留较大安全储备。

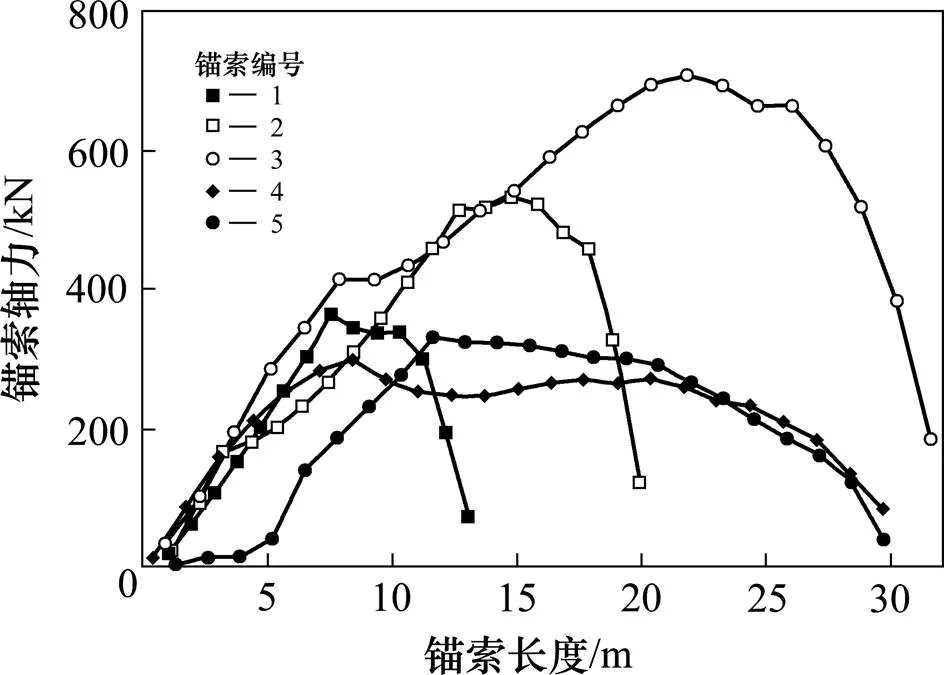
图9 锚索轴力沿长度分布

各根微型桩弯矩分布见图10，各桩弯矩分布基本一致，最大弯矩出现位置与图6的2个潜在滑动面位置一致。说明岩质坡体刚度较大且位移模式一致，与土质边坡显著不同。浅层滑动面对应各桩最大弯矩位置，深层滑动面对应弯矩较小，与相应安全系数趋势一致。上台阶微型桩弯矩较下台阶微型桩弯矩稍大，各桩最大弯矩均在10~20 kN∙m之间，保留了较大强度储备。

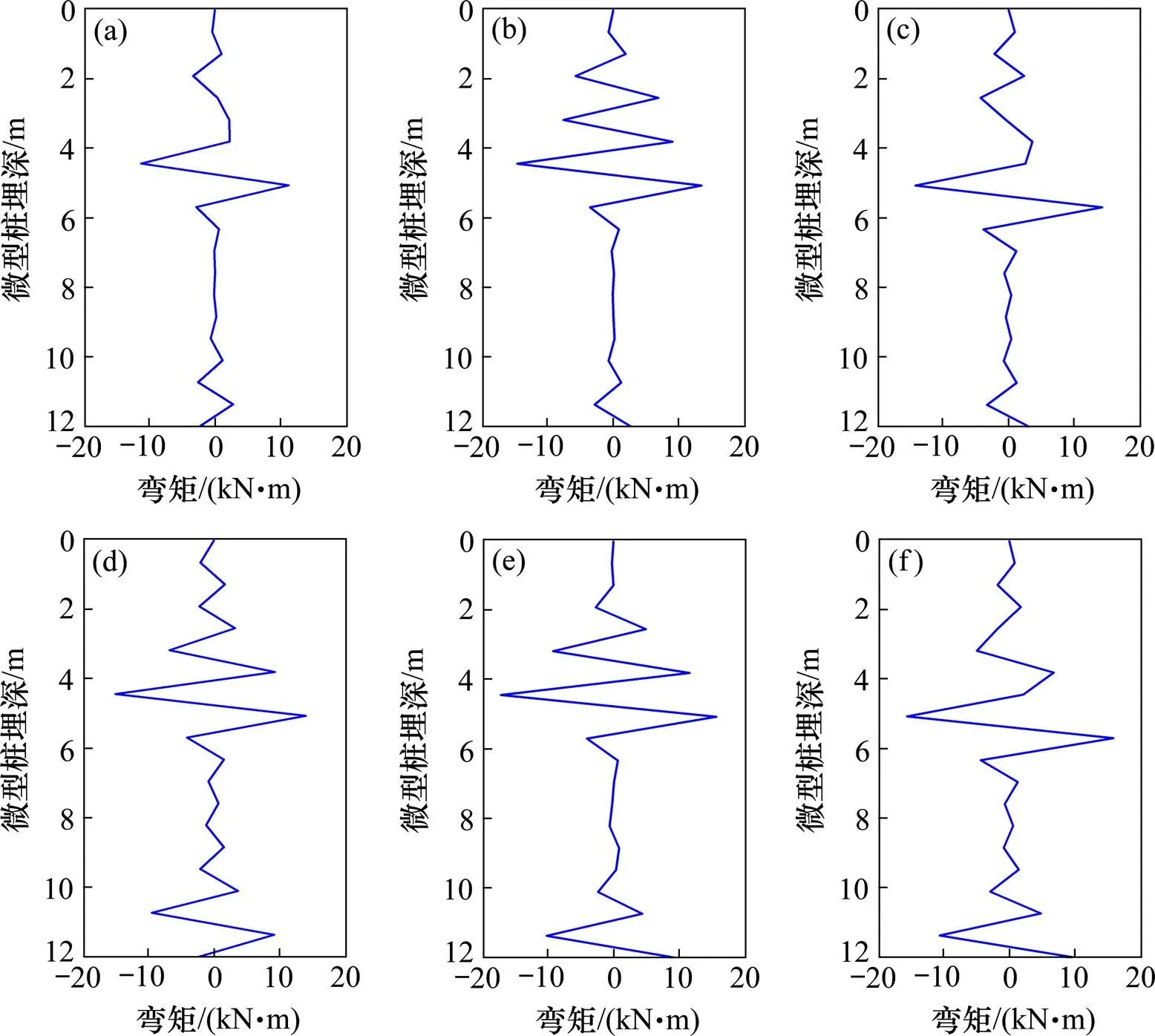
图10 微型桩弯矩沿桩深分布

5 结论

1) 数值模拟结果表明，采用微型桩+锚索联合支护后边坡的安全系数得到显著提高；边坡的潜在失稳模式由中层的沿软弱层面滑动转变为浅层坡体圆弧型滑动。

2) 微型桩和锚索支护的内力与坡体滑动趋势密切相关，预应力锚索的轴力取决于坡体变形大小；微型桩最大弯矩与坡体的内部滑动面基本 一致。

3) 微型桩−锚索联合支护结构在顺层滑坡中表现为良好的适用性。与抗滑桩方案相比，两者虽然造价相当，但是微型桩方案因施工速度快，施工过程安全，越发凸显了其优越性。

[1] 高永涛, 肖术, 吴顺川, 等. 顺层岩质边坡变形破坏特征及稳定性数值模拟[J]. 工程科学学报, 2015, 37(11): 1403−1409. GAO Yongtao, XIAO Shu, WU Shunchuan, et al. Numerical simulation of the deformation and failure characteristics of consequent rock slopes and their stability[J].Journal of University of Science and Technology Beijing, 2015, 37(11): 1403−1409.

[2] 王吉亮, 杨静, 陈又华, 等. 复杂层状高陡岩质边坡变形与稳定性研究[J]. 水利学报, 2015, 46(12): 1414− 1422. WANG Jiliang, YANG Jing, CHEN Youhua, et al. Study on deformation and stability of complex layered high and steep rock slope[J].Journal of Hydraulic Engineering, 2015, 46(12): 1414−1422.

[3] 白松松, 张骞, 高昱, 等. 顺层岩质边坡抗滑桩弯折破坏模型及试验研究[J]. 水利水电技术, 2018, 49(9): 25−31. BAI Songsong, ZHANG Qian, GAO Yu, et al.Study on flexural failure model of anti-slide pile for bedding rock slope and its experiment[J]. Water Resources and Hydropower Engineering, 2018, 49(9): 25−31.

[4] 赵华, 李文龙, 卫俊杰, 等. 反倾边坡倾倒变形演化过程的模型试验研究[J]. 工程地质学报, 2018, 26(3): 749−757. ZHAO Hua, LI Wenlong, WEI Junjie, PANG Bo.Model test study on toppling deformation evolution process of counter-tilt slope[J].Journal of Engineering Geology, 2018, 26(3): 749−757.

[5] 李安洪, 周德培, 冯君. 顺层岩质路堑边坡破坏模式及设计对策[J]. 岩石力学与工程学报, 2009, 28(增1): 2915−2915. LI Anhong, ZHOU Depei, FENG Jun. Failure modes of bedding rock cutting slope and design countermeasures[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Suppl 1):2915−2915.

[6] 谭鑫, 傅鹤林, 陈琛, 等. 层状岩体中隧道稳定性数值分析[J]. 铁道科学与工程学报, 2016, 13(6): 1108−1113. TAN Xin, FU Helin, CHEN Chen, et al. Numerical simulation analysis of tunnel in layered rock-mass[J].Journal of Railway Science and Engineering, 2016, 13(6): 1108−1113.

[7] 肖国峰, 冯光乐, 陈从新, 等. 硬岩中倾顺层边坡变形特征和破坏机制分析[J]. 岩石力学与工程学报, 2007, 26(增2): 4458−4464. XIAO Guofeng, FENG Guangle, CHEN Congxin, et al. Reserach on deformation and failure mechanism of moderate-dip cataclinal hardrock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl 2): 4458−4464.

[8] 成永刚. 顺层滑坡数值模拟与监测分析[J]. 岩石力学与工程学报, 2008, 27(增2): 3746−3752. CHENG Yonggang. Chinese journal of rock mechanics and engineering[J]. Chinese Journal of Rock Mechanics And Engineering, 2008, 27(Suppl 2): 3746−3752.

[9] 成永刚, 王玉峰. 层面倾角对顺层岩质滑坡贡献率研究[J]. 岩土力学, 2011, 32(12): 3708−3712. CHENG Yonggang, WANG Yufeng. Research on contribution rate for dip angle of bedding landslide[J]. Rock and Soil Mechanics, 2011, 32(12): 3708−3712.

[10] 杜衍庆, 王新岐, 冯炜, 等. 微型桩群−锚索地梁体系加固斜坡路基的原位试验研究[J]. 公路, 2017, 62(9): 120−126. DU Yanqing, WANG Xinqi, FENG Wei, et al.In-situ monitoring study of strengthened slope subgrade for micro-pile group and anchor cable ground beam system[J]. Highway, 2017, 62(9): 120−126.

[11] 胡田飞, 梁龙龙, 朱本珍. 微型桩−锚组合新结构抗滑特性的数值分析[J]. 地下空间与工程学报, 2016, 12(5): 1410−1416. HU Tianfei, LIANG Longlong, ZHU Benzhen. Numerical analysis of the anti-sliding characteristics of the new micropile-anchor composite structure[J].Chinese Journal of Underground Space and Engineering, 2016, 12(5): 1410−1416.

[12] TAN X, Konietzky H, Thomas Frühwirt, et al. Brazilian tests on transversely isotropic rocks: Laboratory testing and numerical simulations[J]. Rock Mechanics and Rock Engineering, 2015, 48(4): 1341−1351.

[13] 谭鑫, Heinz Konietzky. 含层理构造的非均质片麻岩巴西劈裂试验及离散单元法数值模拟研究[J]. 岩石力学与工程学报, 2014, 33(5): 938−0946. TAN Xin, Heinz Konietzky. Brazilian split tests and numerical simulation by discrete element method for heterogeneous gneiss with bedding structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 938−946.

[14] GUI Y L, ZHAO Z Y, Kodikara J, et al. Numerical modelling of laboratory soil desiccation cracking using UDEC with a mix-mode cohesive fracture model[J]. Engineering Geology, 2016(202): 14−23.

[15] Cundall P A, Hart R D. Development of generalized 2-D and 3-Ddistinct element programs for modelling jointed rock[R]. U S: Army Corps of Engineers, 1985.

[16] Cundall P A, Hart R D. Numerical modeling of discontinue[C]// Comprehensive Rock Engineering. Oxford: Pergamon Press, 1993: 193–213.

[17] Cundall P A. UDEC—a generalized distinct element program for modelling jointed rock[R]. US：US Army Corps of Engineers, 1980.

Stability analysis of bedding rock shope reinforced by micro-piles and prestressed anchor

JIANG Hua

(Hunan Communications Research Institute Co., Ltd., Changsha 410005, China)

Based on the engineering geological conditions of K128 bedding slope of Heng-shao expressway, a numerical model of block discrete element method for the combined support of micro-piles and anchor cables for bedding rock slope was established by UDEC in this paper, considering the spatial distribution pattern of bedding and joint discontinuous surface and the softening characteristics of marl bedding. The numerical model reflects the influence of the key influencing factors such as the strength of the structural surface, the thickness of the rock layer and the dip Angle of the rock layer on the failure and instability mode of the bedding rock slope. Numerical model, based on the discrete element method in this paper, through the analysis of micro pile and anchor rope combined support scheme of the numerical simulation results, the following conclusions. The potential failure mode of the reinforced slope changes from the original sliding along the soft layer to the approximate circular arc sliding along the shallow layer.

bedding; slope; micro-piles; discrete element method; numerical simulation

TU472

A

1672 − 7029(2019)09−2184 − 08

10.19713/j.cnki.43−1423/u.2019.09.008

2018−11−30

湖南省交通运输厅资助项目(201501)；湖南省交通科技项目(201311)

姜华(1973−)，女，湖南湘阴人，高级工程师，从事公路工程设计、咨询、检测及科研工作；E−mail：457054644@qq.com

(编辑 蒋学东)