浅埋暗挖隧道施工风险综合评价方法

欧智勇，傅鹤林，黄震，张福权，赵涛涛

浅埋暗挖隧道施工风险综合评价方法

欧智勇1，傅鹤林2，黄震2，张福权1，赵涛涛1

(1. 中铁隧道局集团三处有限公司，广东 广州 511400；2. 中南大学 土木工程学院，湖南 长沙 410075)

浅埋暗挖隧道工程施工具有许多不确定性风险因素，需要对风险事件进行安全等级确定和风险优先排序。采用模糊逻辑与失效模式影响分析、故障树分析和层次分析法-数据包络分析相结合的方法，提出浅埋暗挖隧道工程施工风险综合评价新方法，可为浅埋暗挖隧道施工风险重要事件的筛选提供一种实用、合理的方法。将该方法应用于广东金光东隧道浅埋暗挖矿山隧道工程的施工风险评估，结果表明：洞门破除土体失稳风险和对周边环境风险(古树、电塔等)优先级RPN值均＞0.4，且＜0.55，风险等级为2级，因此，针对这些风险事件需要采取风险控制措施进行预防。其他风险事件的风险等级为3级，风险可接受，可采取安全控制措施。

浅埋暗挖隧道；风险综合评价；模糊集；故障树；FMEA

城市地下空间的快速扩张，大量地下工程不断涌现，其中隧道工程为当前发展规模最大的地下空间工程[1]。由于具有投资大、环境多变、技术难度大、周期长、不可预见的风险因素多和地质条件复杂的特点，隧道工程建设过程中的风险因素众多，极易引起各类风险事件[2]。尤其是浅埋暗挖隧道，通常地质条件差、受周边环境影响大、埋深浅及施工控制难，施工过程中的风险极大，需要对其进行必要的施工安全风险评价，以便于工程风险控制和减少风险事故。施工风险管理是识别风险来源，并分析风险影响，最终通过开发相应管理工具来实现项目的风险管理[3]。风险管理涉多种方法，包括风险的识别、风险评估、风险控制和风险监测等[4]。对于风险评估过程，许多学者提出了一系列方法。其中模糊评价方法由于具有反映评价对象模糊性的特点，已经成熟地应用于各行各业的风险项目管理中[5]。例如，在隧道工程中，程远等[6]采用模糊数学方法定量化处理施工风险评价中的定性问题，并建立了跨度隧道施工风险多层次模糊综合评价模型；张东明等[7]基于综合超前地质预报和模糊层次评价方法，建立深埋长隧道地质灾害风险评价预测机制；黄越等[8]采用专家调查法、层次分析法、主成分分析法和BP神经网络法，提出隧道洞口段施工阶段风险模糊神经网络评估方法。王頠等[9]基于现有隧道风险模糊评价模型，提出一种隧道总体风险评价的模糊评判改进方法。了解风险产生的根本原因分析可帮助项目管理者找到风险控制的关键点，以实现积极应对风险的策略，实现最大限度的减少风险源。本文结合模糊逻辑与失效模式影响分析(FMEA)、故障树分析(FTA)和层次分析法−数据包络分析(AHP-DEA)相结合的方法，提出一种浅埋暗挖矿山法隧道施工风险综合评价方法。该方法有助于改进施工风险安全管理，为浅埋暗挖矿山法隧道施工风险重要事件的筛选提供一种实用、全面的方法。将该方法应用于广东金光东浅埋暗挖矿山法隧道工程的施工风险评估，为该工程的施工风险控制提供依据。

1 工程概况

广州金光东矿山隧道下穿新造镇元岗山古树群，包括28棵乌榄古树和34棵荔枝古树，树龄均在100 a以上，根茎深度大约5 m，为挂牌保护的古树名木。由于古树树龄较高，移植难度大，因此不考虑迁移，该段隧道采用矿山法暗挖通过。

金光东隧道为双向4车道城市主干道，全长440 m。隧道限界净高4.5 m，隧道埋深约为5.17~ 18.21 m。隧道断面采用双洞分离式马蹄形断面。矿山段均位于Ⅴ级围岩地段，按照新奥法原理为基础，采用四部CRD开挖法。

该隧道工程广泛分布第四系填土，中细砂及粉质黏土组成，部分地段由建筑垃圾或块石组成，土质不均匀。隧道下伏基岩为花岗岩，其风化残积土主要为砂质黏性土或砾质黏性土，在遇水或施工扰动时，土体强度、稳定性及围岩级别降低，对隧道的稳定性及承载力有影响。该隧道地势较高，区内地下水以松散岩类孔隙潜水为主，基岩裂隙水水量贫乏，主要接受大气降水入渗及沟谷流水补给，含水层位于风化岩层中，地下水位埋深约为1.09~4.05 m。金光东隧道平、纵断面横断面如图1所示。

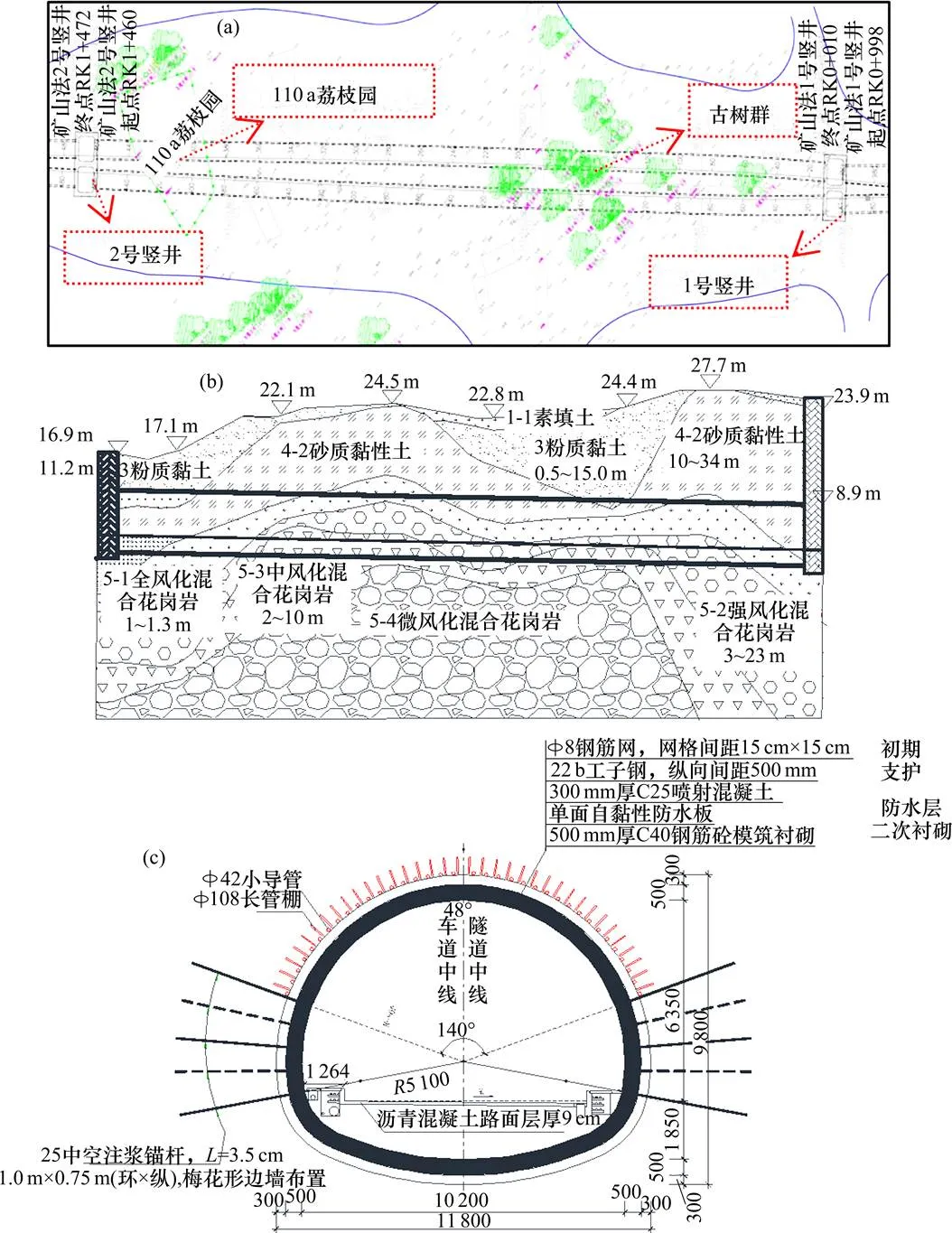
(a) 平面图；(b) 纵断面图；(c) 隧道横断面图

2 施工风险分析方法

2.1 模糊集理论

模糊集理论是Zadeh提出的[10]。在研究不确定的或模糊的对象时，该理论可以很好地反映事物的不确定性和模糊性。

2.1.1 模糊隶属函数

有许多不同类型的模糊隶属函数，如三角形模糊数，梯形模糊数和高斯模糊数。比较而言，梯形模糊数隶属函数能更好地处理实际决策信息，反映因素不确定性和决策者的主观性[5]。本文利用梯形隶属函数对专家认知中的主观不确定性和模糊不确定性进行量化。如图2所示，可将梯形模糊数定义为(1，2，3，4)。

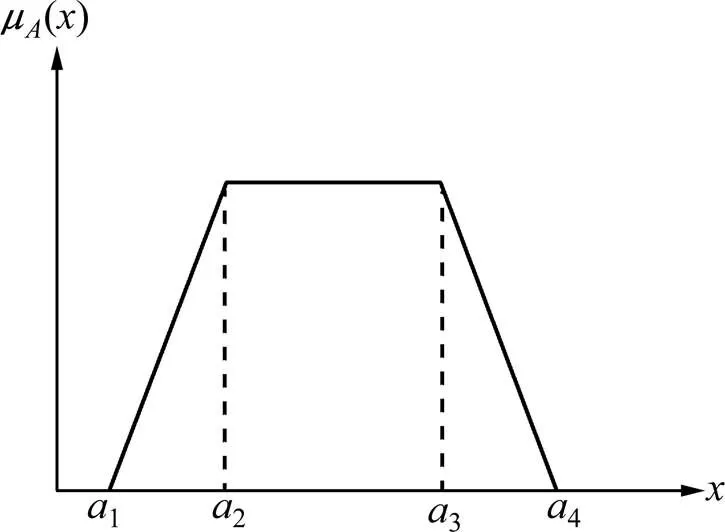
图2 梯形模糊数A

2.1.2 模糊集的截集

为便于数值计算，通常将模糊数表示为有限个-截集的上界和下界集合。对于梯形模糊数(，，，)，采用式(1)和式(2)可分别用于计算每个-截集水平方向上的下限和上限：

下限= (a+ (b−a)) (1)

上限= (d−(d−c)) (2)

如果和是区间α=[1,1]，α=[2,2]上表示的2个模糊集合，那么α+α，α−α和α×α可被定义为以下表达式：

(A+B)=α+α[12,1+2] (3)

(A−B)=α−α[12,1−2] (4)

(A×)=α×α[min(1×2,1×2,1×21×2)

max(1×2,1×2,1×2,1×2)] (5)

2.1.3 去模糊化

依据反映实际情况、简便易行、高效以及评估组观点的要求，采用式(6)进行去模糊化处理：

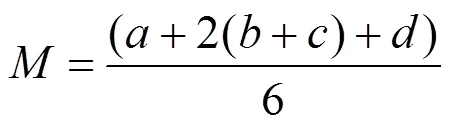
2.2 失效模式与效应分析

失效模式和效应分析(FMEA)是一种能够定义、识别和消除来自系统、设计或过程的已知及潜在的故障、问题和错误的工程技术。根据传统的FMEA方法，通过计算风险优先数(RPN)来确定故障模式的临界程度。将严重程度(S)、发生度(O)和检测/控制难易度(D)的值相乘，得到风险优先数(RPN)，即＝××。

由于传统的FMEA方法存在缺陷。因此，引入模糊数来取代清晰数字来测量，，。这些模糊数可以是基于专家判断或其他技术语言变量。

2.3 故障树分析

故障树分析方法(FTA)最初是在1960~1961年贝尔电话实验室开发的[11]。FTA通过关系图形来追溯系统的危害，最终找到其根本原因。收集足够的统计数据来准确评估故障率往往是困难的。为了克服这个问题，可结合模糊集理论。故障树分析用于识别风险的根本原因和评估顶上事件发生概率。

假设事故树中不含重复或相同基本事件，各事件互相独立，顶上事件发生概率可根据故障树结构采用以下公式计算。

采用“与门”连接的顶上事件的发生概率为：

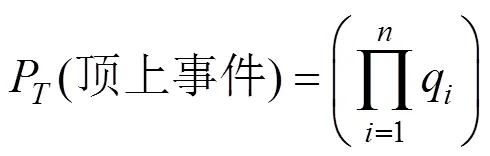
采用“或门”连接的顶上事件的发生概率为：

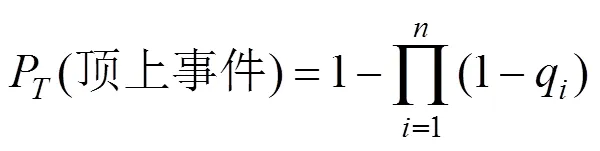
式中：q为第个基本事件的发生概率(=1,2,…,)。

本文采用-截集的概念来计算顶上事件发生的概率。基于-截集概念的“与”门及“或”门的模糊数形式的故障树顶上事件的概率可以分别通过式(9)和式(10)得到：

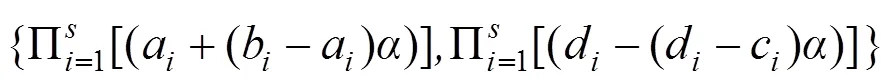
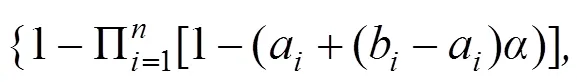
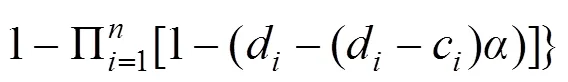
2.4 层次分析法-数据包络分析

层次分析法是一种多准则决策方法，通过该方法可以评估备选方案并计算其费率。AHP适用于主观专家判断和使用定性和定量数据的决策情况。

在AHP方法中，将比较结果形成判断矩阵，并计算标准权重。如果有个标准被确定用于比较，AHP通过以下步骤来计算这些标准的权重。

1) 为个目标创建(×)维的判断矩阵， 如下：

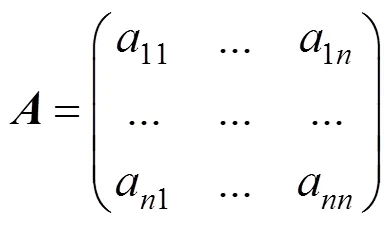
式中：a表示第个目标比第个目标重要多少。对于矩阵中所有的s 和s，必须满足a= 1和a= 1/a。

2) 将列中的每个值除以列中所有值的总和。得到的新矩阵种每一列的值的总和为1，形成的归一化判断矩阵为：

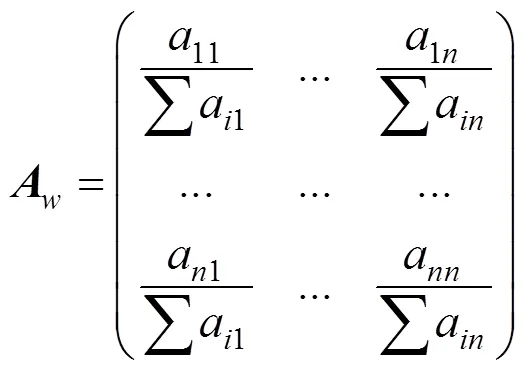
3) 通过找到矩阵的主特征向量来计算c。计算c作为矩阵中第行中所有值的平均值，最终得到列向量。列向量中的值表示第个目标的权重。

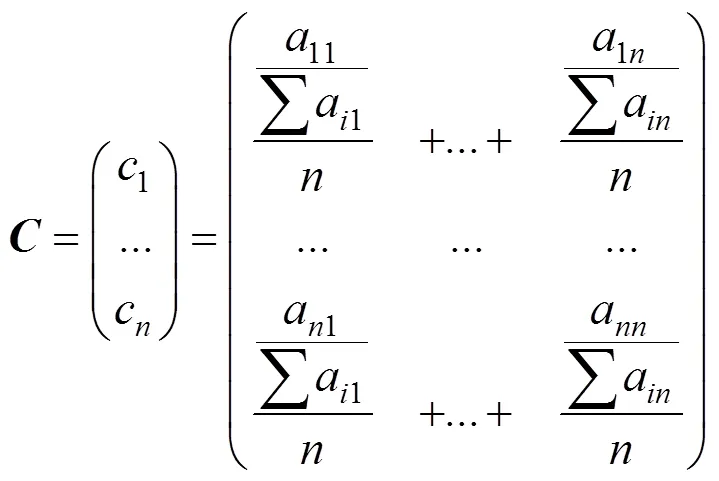
4) 检查权重值(c)的一致性。为了确定一致性，需要进行以下步骤。

首先，计算×矩阵(一致性向量)：

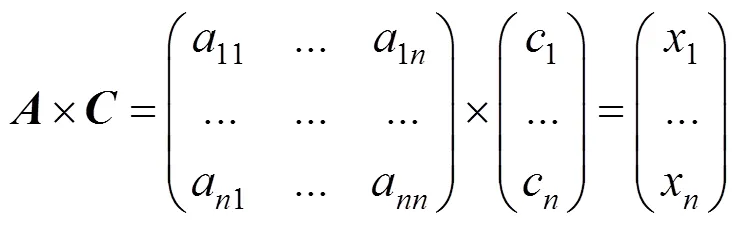
其次，通过×计算x，x是比特征向量更好的近似值，可采用以下公式计算max：

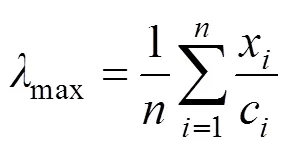
max为判断矩阵的特征值。然后采用以下公式计算一致性指数结果。

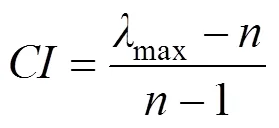
最后，为确保判断矩阵的一致性，须通过CR控制一致性判断为合适的值，即：

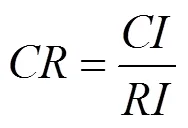
式中：是随机一致性指数，当≤0.10，则其一致性满足要求。如果＞0.1，则存在不一致性，则AHP计算结果没有意义。

对于个决策选项，采用判断矩阵，如果给定大量不同的标准和决策选项，决策者将需要进行大量的比较分析。为解决这类问题，可采用数据包络分析(DEA)的AHP方法。

为明确每个风险的相对重要性，为每个标准给出备选方案，并且根据式(18)为每个标准引入一组评估度：

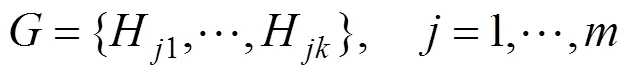
式中：Hl到H表示标准的评估分数从最高显著性到最低显著性，k表示每个标准的评估分数。

如果标准将由N专家评估，那么结果可以由根据式(19)的分布评价向量表示：

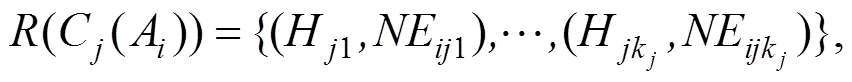
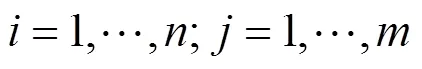
此时，用于确定(H)值的DEA模型可以表 述如下。

最大化：

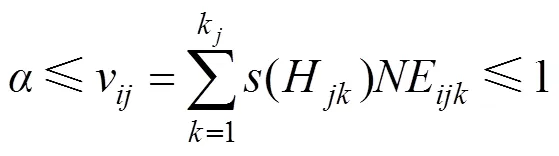
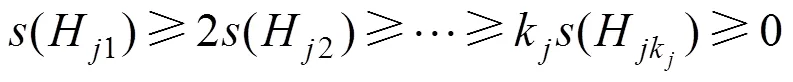
式中：(H1)，…，(H)为决策变量。然后，指出每个决策备选方案的局部权重也可以用式(21)中的信任结构来定义：

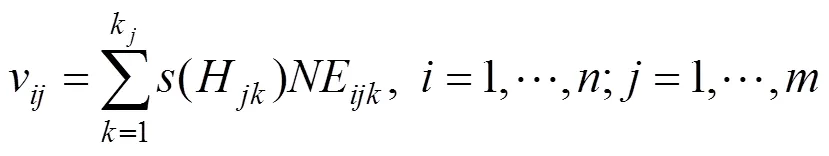
最后，可以通过式(22)生成总体权重：

式中：w(＝1,…,)是由AHP方法确定的因素权重；v是DEA方法确定的局部权重(式(21))；(A)(=1,…,)是个备选方案的总权重。基于以上权重，个备选方案可进行优先排序或排序。

3 隧道施工风险综合评价模型

基于第2节各施工风险分析方法，构建隧道工程施工风险综合评价模型，该模型由4个阶段组成，如图3所示。

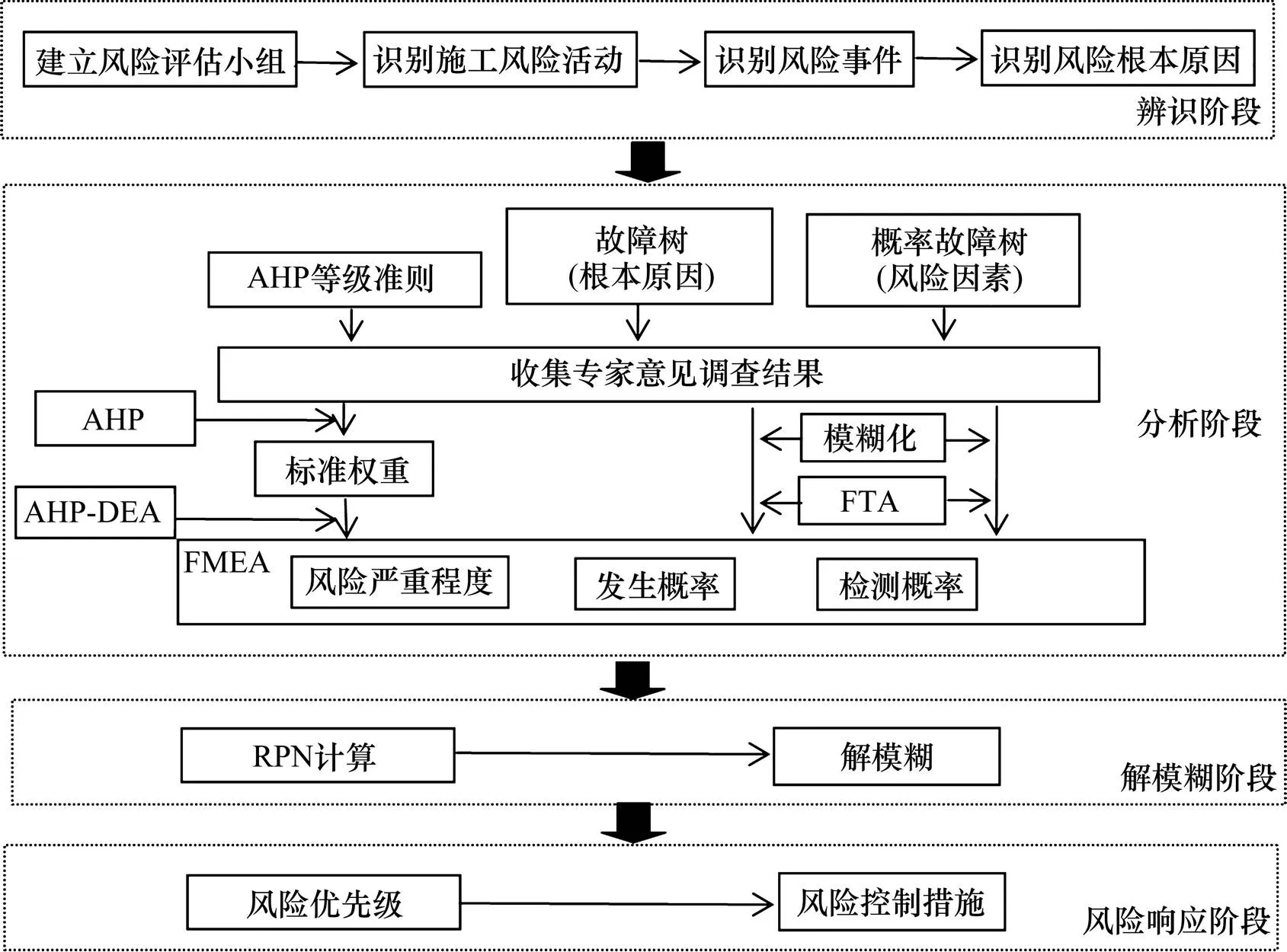
图3 施工风险评估模型的流程图

3.1 风险辨识

由隧道工程专业的专家、科研单位技术人员、设计院技术人员、监理工程师以及项目部技术人员组成的大型建设项目风险评估小组，总人数不少于10人。对工程项目的任务及风险源进行辨识和 验证。

3.2 风险分析

针对风险、因素和不期望事件的原因，建立一个层次结构。在模糊FTA中，通过给基本事件的概率赋值并计算传播概率，来确定顶上事件发生的概率。在此，采用语言变量(非常低、低、中、高和非常高)为故障树和每个风险的影响准备调查问卷。然后分配给行业专家、科研技术人员和设计院技术人员及监理工程师等，并由他们填写完成。专家组需要使用语言术语来评估基本事件发生的模糊概率。本文采用语言变量及对应梯形模糊数如表1所示。图4为不同语言变量所对应的模糊隶属度函数。因此，通过将基本事件的模糊概率代入方程(10)得到不同的-截集下的顶上事件的模糊概率。该方法同时用于计算发生概率和风险检测/控制概率。

然后，结合AHP-DEA方法来计算风险影响因素的权重。考虑风险因素对4个指标的影响，即个人的伤害、财产损失、施工进度和环境影响。利用专家的认知(通过收集问卷中的调查结果)，进行相互比较，并使用AHP方法，对个人伤害、财产损失、施工进度和环境影响进行加权。

表1 发生概率和识别危险对应的评估语言变量

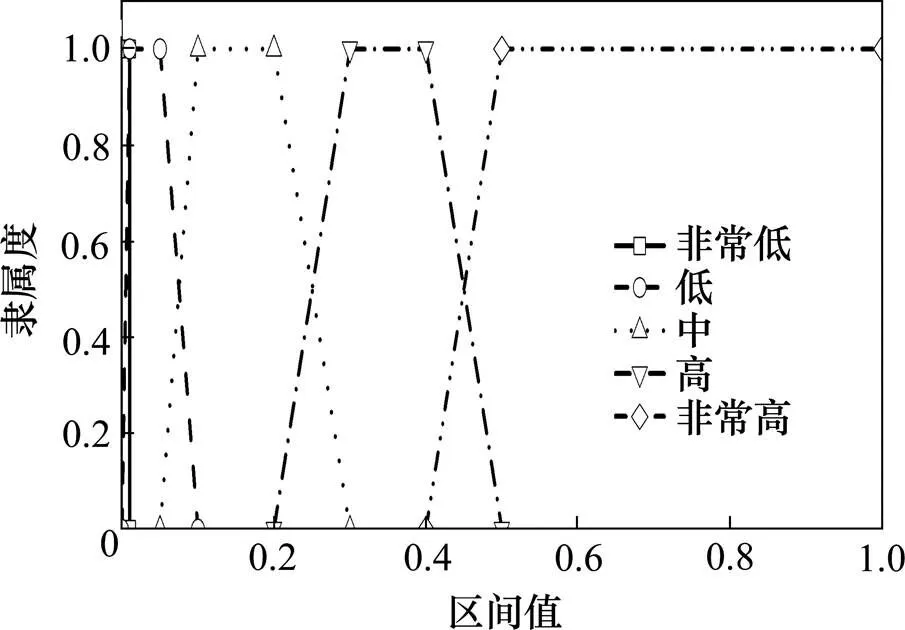
图4 语言评价值的隶属函数

最后，根据模糊FMEA方法，对每个识别风险的，和结果进行分析。

3.3 风险优先数与风险响应

结合-截集和式(5)，将，和3个参数相乘得到风险优先数(RPN)。最后使用式(6)对RPN进行去模糊化处理。根据RPN对风险事件进行排序，并对那些具有较高优先级的风险采取必要进一步的风险控制分析，并提出对应的预防措施。

4 矿山法段施工风险分析

4.1 风险识别

在调查隧道浅埋暗挖矿山隧道工程事故的基础上，分析本项目的周边建筑环境、水文地质条件、施工工艺、人员管理和施工进度等情况，并咨询了隧道行业专家和安全技术管理人员之后，确定7个常见的风险事件，见表2。

4.2 故障树分析法

绘制风险故障树来分析其根本原因。通过返回的问卷数据来计算风险发生概率，并基于对应的调查问卷来计算风险检测/控制概率。

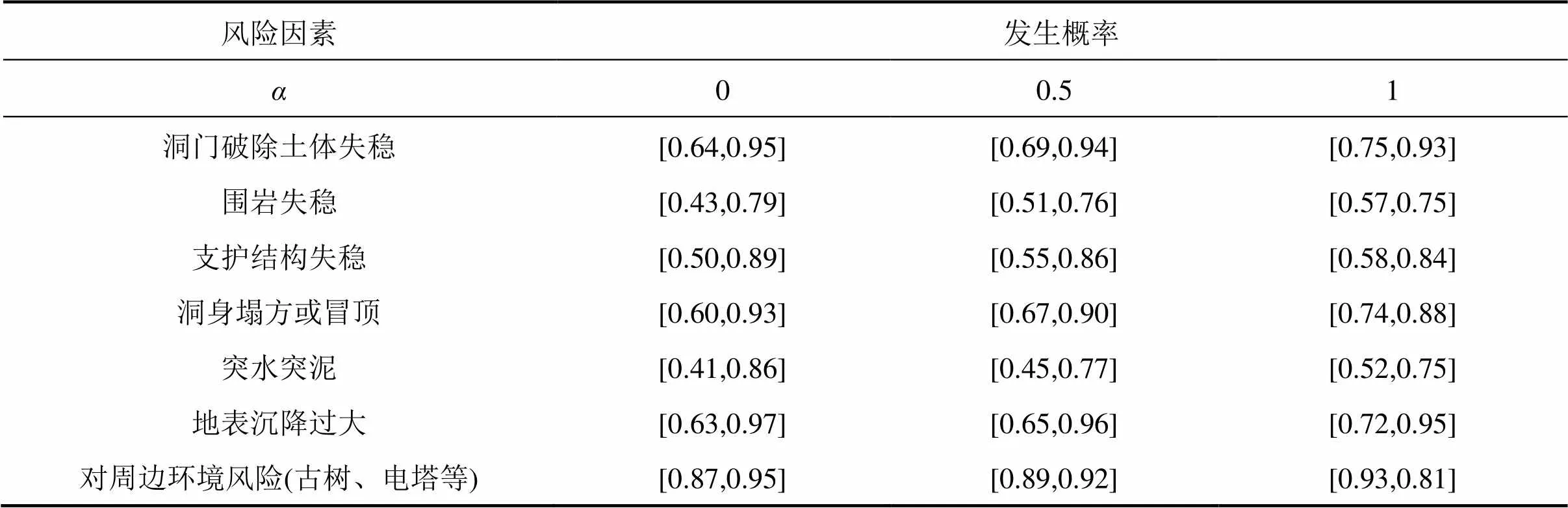
表2 7种风险事件的模糊发生概率的α-截集

4.3 计算发生概率

利用式(1)中所定义的上、下限方程，并结合式(9)和式(10)，顶上事件的模糊概率可表示为：

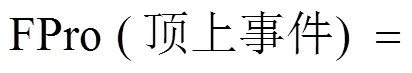
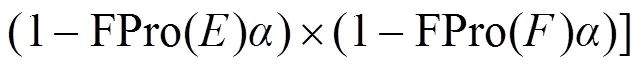
结合式(23)，可通过递增α值来计算顶上事件的模糊概率。

利用式(5)求解等式(10)中的乘法算子，利用式(23)计算顶上事件((=0,0.5和1)发生的模糊概率。然后将基本事件的模糊概率代入式(23)得到不同截集下顶上事件的模糊概率的计算结果如表2 所示。

4.4 计算检测概率

为了计算风险检测难易度概率，识别风险的根本原因，并绘制用于所有风险的检测故障树，如图6所示。根据发生概率计算的过程，计算该项目的风险检测概率，其检测故障树分析结果见表3。

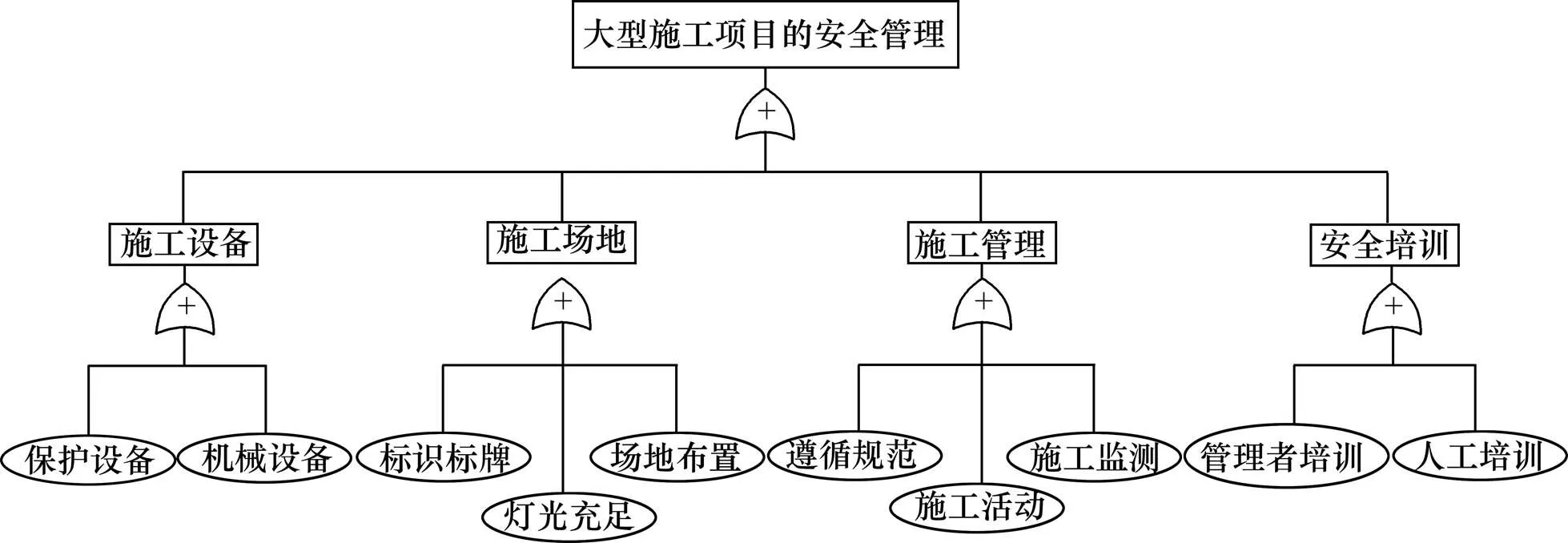
图6 风险检测概率的故障树

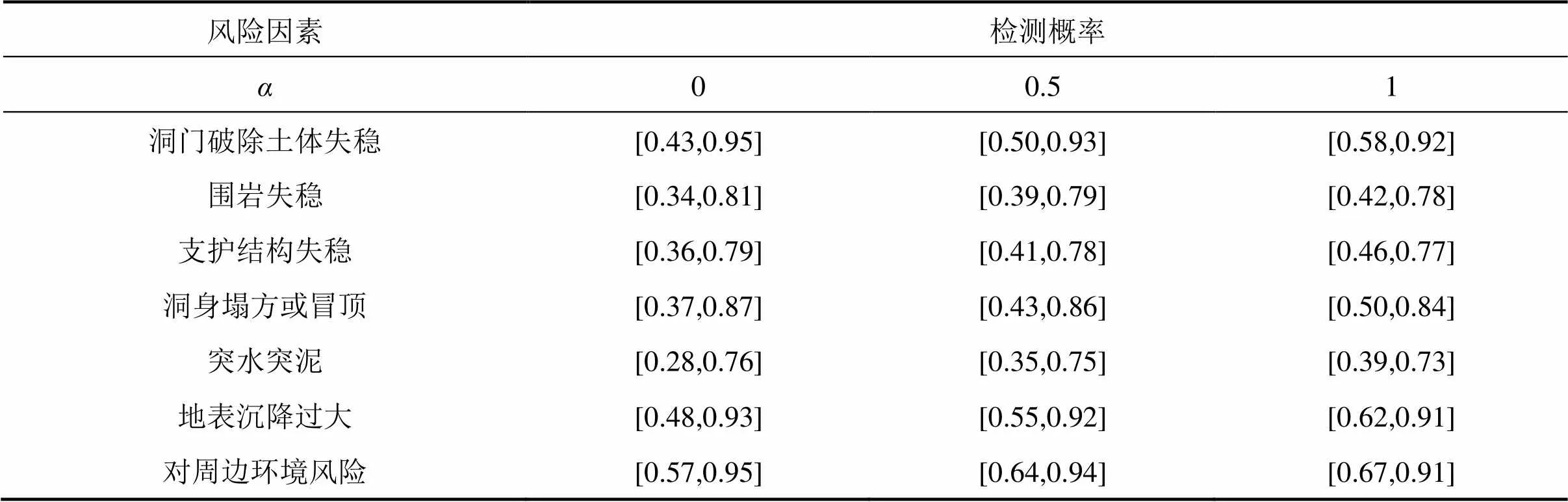
表3 模糊检测概率的α截集

4.5 计算风险影响

结合AHP-DEA方法计算风险影响的权重。考虑了风险因素对4个指标的影响，即个人伤害、财产损失、施工进度和环境影响。利用专家调查结果，从个人的伤害、财产损失、施工进度和环境影响4个角度出发，对风险因素进行两两比较，并采用式(11)~(13)，对个人伤害、财产损失、施工进度和环境影响进行加权处理，结果为0.323，0.253，0.240和0.207。结合DEA方法，根据式(19)~(20)计算每个子因素的权重。

采用式(20)求解4个因素的局部风险得分。此处局部权重可理解为风险评估应用中的局部风险分数。对于个人伤害，采用式(20)得到以下最优解：

(非常高)=0.050 4，(高)=0.040 2，(中)=0.031 9，(低)=0.020 2，(非常低)=0.010 6

此外，根据式(20)得到的财产损失、施工进度和环境影响的最优解为：

(非常高)=0.069 4，(高)=0.058 7，(中)=0.046 2，(低)=0.026 2，(非常低)=0.015 5

(非常高)=0.072 7，(高)=0.063 2，(中)=0.054 2，(低)=0.032 1，(非常低)=0.016 4

(非常高)=0.079 1，(高)=0.069 4，(中)=0.056 3，(低)=0.035 2，(非常低)=0.018 7

基于上述最优解，通过式(21)计算4个标准中的每个局部风险得分，结果见表4。

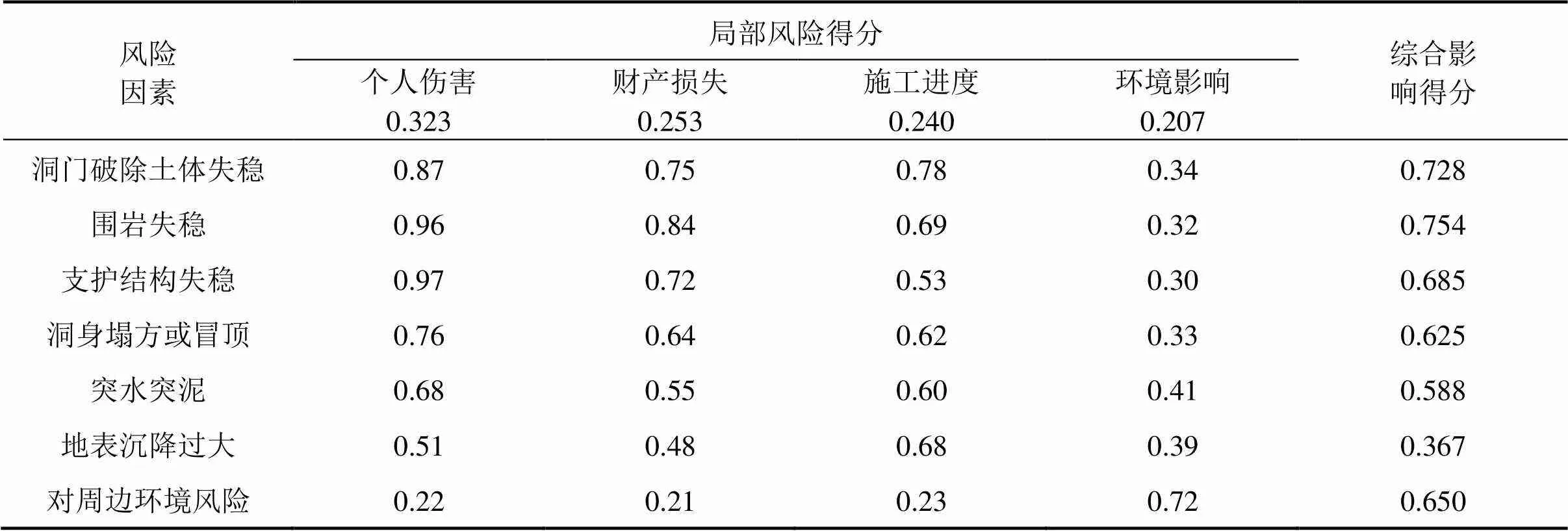
表4 风险严重程度总分

最后，结合式(22)得到一个风险因素的综合影响得分，见表4。以第1个风险因素为例，采用式(22)计算的洞门破除土体失稳风险的综合影响分数如下：

综合影响分数=(0.323×0.87)+(0.253×0.75)+ (0.240×0.78)+(0.207×0.34)=0.728

4.6 风险优先数

根据发生概率的计算结果，得到每个风险的影响和检测概率，即风险优先数(RPN)，并对风险进行评级排序，结果见表5。以洞门破除土体失稳为例，根据表2和表3中=0，1时的概率计算结果和表4中的风险严重程度计算结果，洞门破除土体失稳风险的，和值分别为：

=(0.64,0.75,0.93,0.95)

O0=[0.64,0.95],O1=[0.75,0.93]

=(0.43,0.58,0.92,0.95)

D0=[0.43,0.95],D1=[0.58,0.92]

=0.728

采用式(5)可求解乘法算子，计算=0和=1的RPN如下：

10=××=0.728×[(0.64×0.43,0.95×

0.95)] =[0.200,0.657]

11=××=0.728×[(0.75×0.58,0.93×

0.92)]=[0.317,0.623]

=(0.200,0.317,0.623,0.657)

根据式(6)，结合RPN计算结果，得到洞门破除土体失稳的去模糊化值。

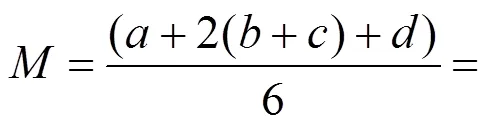
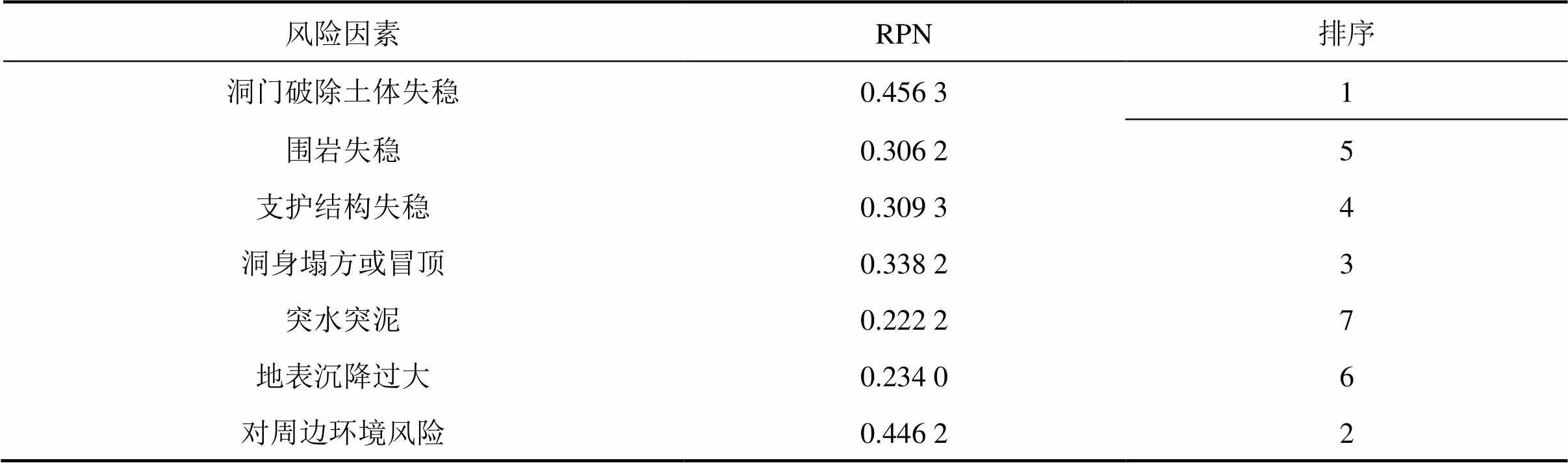
表5 风险因素的优先数

为便于风险控制，对具有较高优先级的风险可以作为优先风险控制事项，如表6所示，表中风险等级划分是参考《城市轨道交通地下工程建设风险管理规范》[12]进行划分的。上述风险事件的优先数RPN分值中，洞门破除土体失稳风险和对周边环境风险(古树、电塔等)RPN值均＞0.4，且＜0.7，风险等级为2级，因此，针对这些风险事件需要采取风险控制措施进行预防。其他风险事件的风险等级为3级，风险可接受，可采取安全控制措施。

表6 施工安全风险等级

5 验证分析

为验证所提方法的合理性，结合程远等[13]提出的基于模糊理论浅埋公路隧道施工风险评估方法进行验证分析。程远等[13]所提方法运用模糊理论对专家给出的隧道施工各项风险因素的概率等级和损失等级隶属度进行统计分析，得到各因素的概率及损失估计结果，最后，采用加权平均法对评判指标进行处理，以确定风险等级。

结合本文中的矿山隧道工程风险因素，依据8个行业专家(一类专家4人，二类2人，三类2人)调查结果确定各个风险因素的概率等级和风险损失等级[13]，见表7。然后基于=×模型考虑风险发生概率和风险损失对风险评估的影响，建立风险评价矩阵，风险等级依据表6划分原则进行，计算结果见表8。从对比结果可看出，本文计算方法与文献[13]方法得到的结论一致。

表7 风险因素的风险概率和损失估计结果

表8 验证分析结果

6 结论

1) 广东金光东隧道浅埋暗挖矿山隧道工程的风险事件的优先数RPN中，洞门破除土体失稳风险和对周边环境风险(古树、电塔等)RPN值均＞0.4，且＜0.55，风险等级为2级，针对这些风险事件需要采取风险控制措施进行预防。其他风险事件的风险等级为3级，风险可接受，可采取安全控制措施。

2) 提出的隧道施工风险综合评价方法，能反映施工风险因素对个人的伤害、财产损失、施工进度和环境的影响程度。对比验证结果表明该方法具有一定可靠性，可为浅埋暗挖矿山隧道施工风险重要事件的筛选和风险等价评价提供一种新方法。

[1] 魏丹. 基于故障树和层次分析法的地铁施工风险评价—以隧道竖井基坑围护结构失稳为例[J]. 安全与环境工程, 2018, 25(1): 100−104. WEI Dan. Risk assessment for subway construction based on fault tree analysis and analytical hierarchy process: a case study of destabilization of pit supporting structure of tunnel shaft[J]. Safety and Environmental Engineering, 2018, 25(1): 100−104.

[2] 郑涛, 孙捷城, 王国富. 地铁隧道矿山法施工事故风险分析与评价[J]. 铁道科学与工程学报, 2018, 15(5): 1356−1362. ZHENG Tao, SUN Jiecheng, WANG Guofu. Risk analysis and evaluation of mine tunnel construction accidents[J]. Journal of Railway Science and Engineering, 2018, 15(5): 1356−1362.

[3] 黄震, 傅鹤林, 尹光明, 等. 地铁隧道结构灾变模型及应用研究[J]. 灾害学, 2018, 33(3):216−221, 228.HUANG Zhen, FU Helin, YIN Guangming, et al. Study on catastrophic model of subway tunnel structure and its application[J]. Journal of Catastrophology, 2018, 33(3): 216−221, 228.

[4] 黄宏伟, 边亦海. 深基坑工程施工中的风险管理[J]. 地下空间与工程学报, 2005, 1(4): 611−614.HUANG Hongwei, BIAN Yihai. Risk management in the construction of deep excavation engineering[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(4): 611−614.

[5] 黄震, 傅鹤林, 黄宏伟, 等. 一种运营地铁盾构隧道结构健康状况评价方法[J]. 地下空间与工程学报, 2018,14(5): 1410−1418.HUANG Zhen, FU Helin, HUANG Hongwei, et al. A method for evaluating the health condition of operation metro shield tunnel structure[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(5): 1410− 1418.

[6] 程远, 朱合华, 刘松玉, 等. 基于模糊理论大跨浅埋公路隧道施工风险评估[J]. 地下空间与工程学报, 2016, 12(6): 1616−1622. CHENG Yuan, ZHU Hehua, LIU Songyu, et al. Risk assessment for construction of large-span and shallow buried highway tunnels based on fuzzy theory[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(6): 1616−1622.

[7] 张东明, 白永杰, 白鑫, 等. 深埋长隧道施工地质灾害风险模糊层次评价[J]. 安全与环境学报, 2018, 18(1): 50−55. ZHANG Dongming, BAI Yongjie, BAI Xin, et al. Evaluation and prediction of the geological hazards in the deep-buried long tunnel project through fuzzy- hierarchical analysis[J]. Journal of Safety and Environment, 2018, 18(1): 50−55.

[8] 黄越, 龚珍, 邓祥辉, 等. 基于模糊神经网络的公路隧道洞口段施工阶段风险评估[J]. 工程管理学报, 2018, 32(3): 119−123. HUANG Yue, GONG Zhen, DENG Xianghui, et al. Evaluation of highway tunnel portal construction risk based on the fuzzy neural network method[J]. Journal of Engineering Management, 2018, 32(3): 119−123.

[9] 王頠, 黄斌, 周强, 等. 隧道总体风险评价的改进模糊评判方法[J]. 地下空间与工程学报, 2016, 12(2): 531− 538. WANG Wei, HUANG Bing, ZHOU Qiang, et al. Improved fuzzy assessment method of total risk for tunnel engineering[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(2): 531−538.

[10] Zadeh L. Fuzzy sets[J]. Information and Control, 1965, 8: 38−53.

[11] Vario J K. Fault tree analysis of phased mission system with repairable and non-repairable components[J]. Reliability Engineering and System Safety, 2001, 74(2): 169−180.

[12] GB 50652—2011, 城市轨道交通地下工程建设风险管理规范[S].GB 50652—2011, Code for risk management of underground works in urban rail transit[S].

[13] 程远, 朱合华, 刘松玉, 等. 基于模糊理论大跨浅埋公路隧道施工风险评估[J]. 地下空间与工程学报,2016, 12(6): 1616−1622.CHENG Yuan, ZHU Hehua, LIU Songyu, et al. Risk assessment for construction of large-span and shallow buried highway tunnels based on fuzzy theory[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(6): 1616−1622.

Comprehensive risk assessment method for shallow underground tunnel construction

OU Zhiyong1, FU Helin2, HUANG Zhen2, ZHANG Fuquan1, ZHAO Taotao1

(1. Third Engineering Department of China Railway Tunnel Bureau Group Co., Ltd, Guangzhou 511400, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

There are many uncertain risk factors in the construction of shallow buried tunnels. It is necessary to determine the safety level and prioritize the risk events. In this paper, a new comprehensive evaluation method of construction risk of shallow-buried tunnels was proposed by combining fuzzy logic with failure mode impact analysis, fault tree analysis and analytic hierarchy process-data envelopment analysis. It can provide a practical and comprehensive method for screening important risk events of shallow-buried tunnels. The method was applied to the construction risk assessment of shallow-buried tunnels in Jinguangdong Tunnel. The results show that the risk of instability of the tunnel entrance and Shallow-Buried Section and the priority RPN value of the surrounding environmental risk (ancient trees, electric towers, etc.) are >0.4, and <0.55. The risk level is 3. Therefore, appropriate mining is needed for these risk events. Take corresponding control measures to prevent. The risk level of other risk events is 2, and the risk is low, so some safety control measures can be taken.

shallow buried tunnels; comprehensive risk assessment; fuzzy set; fault tree; FMEA

U45；X93

A

1672 − 7029(2019)09− 2368 − 10

10.19713/j.cnki.43−1423/u.2019.09.032

2018−12−07

国家自然科学基金重点基金资助项目(51538009)；中铁隧道集团科技创新计划项目(2017-43)

傅鹤林(1965−)，男，江西高安人，教授，博士，从事隧道与岩土工程教学与科研工作；E−mail：fu.h.l@csu.edu.cn

(编辑 阳丽霞)