少筋混凝土重力式桥墩抗震性能分析

鲁锦华，陈兴冲，丁明波，张熙胤

少筋混凝土重力式桥墩抗震性能分析

鲁锦华，陈兴冲，丁明波，张熙胤

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

基于2个呈弯曲破坏桥墩的拟静力试验结果，建立适合少筋混凝土重力式桥墩滞回分析的有限元模型，对少筋混凝土重力式桥墩的抗震性能进行研究，分析剪跨比、轴压比和配筋率对桥墩位移延性、刚度退化和耗能能力的影响。研究结果表明：轴压比越大，桥墩的刚度退化速率越快，延性性能越小及耗能能力越弱；剪跨比的增加会使桥墩的刚度退化速率减慢，延性性能增强，但是耗能能力受配筋率的影响较大，配筋率越低，规律越不明显；提高配筋率可以显著提高桥墩的抗震能力；少筋混凝土重力式桥墩破坏时呈现出现脆性破坏特征，延性性能不足。

少筋混凝土；重力式桥墩；数值模拟；抗震性能

目前我国铁路桥墩多采用截面尺寸大、刚度大和质量大的混凝土重力式桥墩[1−3]。重力式桥墩由于配筋率较低(＜0.5%)，属于少筋混凝土结构，其抗震性能不同于钢筋混凝土桥墩。鉴于此，国内不少学者对其进行了研究。鞠彦忠等[4−5]着重研究了配筋率为0.1%和0.2%的圆端型桥墩，通过大比例尺的拟静力试验发现配筋率较低时剪跨比对桥墩耗能的规律不明显，随着配筋率的增加桥墩的塑性变形能力增强，但是所有桥墩均呈现出脆性破坏的特征。为了提高混凝土重力式桥墩的抗震能力，近年来设计的桥梁墩身的配筋率也有所提高，大多在0.3%以上。不少学者对影响此类桥墩的抗震性能进行了研究。蒋丽忠等[6−7]采用正交试验方法研究了高速铁路圆端型桥墩的抗震性能，研究发现延性性能与配筋率有关，配筋率小于0.4%时，延性随配筋率增加而减小，配筋率大于0.4%时，延性随配筋率增加而增加。而赵冠远等[8]认为随着配筋率、剪跨比和配箍率的提高，桥墩的延性性能和累积耗能提高，对桥墩的刚度退化影响较小。王欢[9]利用ABAQUS软件建立了5组不同配筋率的模型墩，发现随着配筋率的增加桥墩的延性降低。周赞[10]研究了不同剪跨比对桥墩抗震性能的影响，发现剪跨比对桥墩耗能能力的影响与地震烈度有关，烈度不同，影响不同。刘浩[11]利用ANSYS软件建立桥墩的实体模型，讨论了配筋率和配箍率对桥墩抗震性能的影响，发现提高配筋率和配箍率均可以提高桥墩的延性性能。李霖[12]认为提高配筋率可以提高桥墩的延性性能和耗能能力，同时可以降低桥墩的刚度退化速率。张永亮等[13−15]研究了不同配筋率对桥墩抗震性能的影响，发现随着配筋率的增加桥墩的塑性变形能力增强，耗能能力增强。从以上研究可以发现不同的参数对少筋混凝土重力式桥墩的影响规律并不一致，这可能是由于研究者试验数量较少而导致得到的规律不一致。因此为了更好地了解少筋混凝土重力式桥墩的抗震性能，本文依据2根少筋混凝土重力式桥墩的拟静力试验数据，建立桥墩的数值分析模型，并分析剪跨比、轴压比和配筋率对桥墩位移延性性能、刚度退化和耗能能力的 影响。

1 少筋混凝土重力式桥墩滞回分析模型

1.1 桥墩计算模型

模型试验桥墩的截面尺寸为64 cm×45 cm，桥墩高为200 cm，配筋率分别为0.3%和0.4%，箍筋间距均为10 cm，剪跨比为5.6。混凝土强度为C30，纵筋和箍筋均选用HRB335钢筋，纵筋直径为8 mm，箍筋直径为6 mm。缩尺后模型桥墩竖向力为57 kN，模型桥墩试验加载如图1所示。采用ANSYS有限元分析软件，建立少筋混凝土重力式桥墩的滞回分析模型，有限元模型见图2。混凝土采用SOLID 65单元模拟，钢筋采用LINK180单元模拟，钢筋与混凝土之间采用COMBIN39单元模拟。竖向力在有限元分析模型中转化为均布荷载施加在墩顶。

图1 试验加载系统

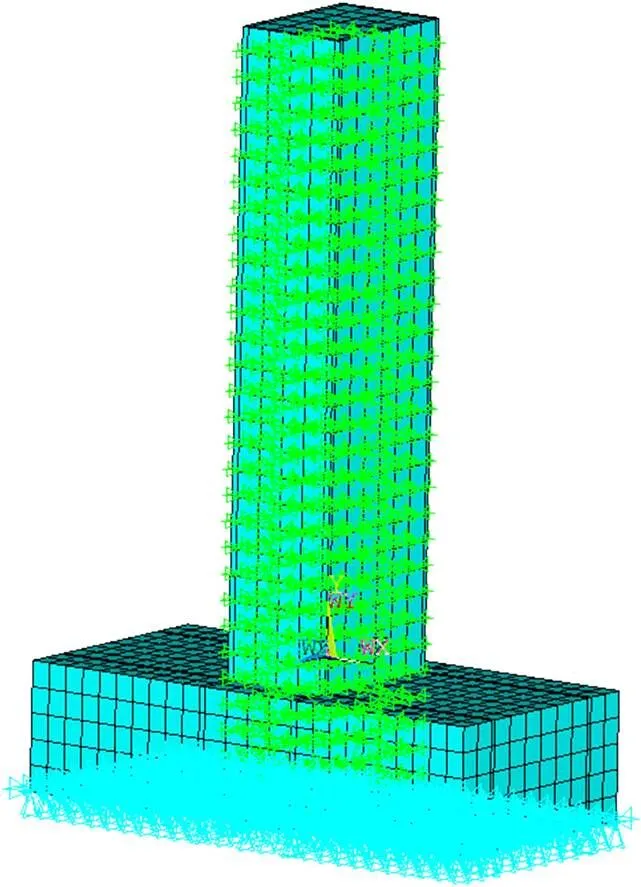
图2 桥墩有限元分析模型

1.2 材料本构关系

1) 混凝土本构模型

约束混凝土的本构影响着模型计算时混凝土受压强度的大小，同时也决定着混凝土受压破坏的全过程。选用国内外比较常用的Mander本构模 型[16]。破坏准则采用的是William-Warnke5参数 准则。

2) 钢筋的本构关系

钢筋的本构关系对桥墩滞回曲线的形状有着重要的影响。Dodd等[17−19]发现钢筋的包辛格效应可以更好地反应滞回曲线的“捏缩”效应，并提出了能够反应钢筋包辛格效应的本构关系。选用ANSYS中提供的可以反应钢筋包辛格效应的多线性随动强化模型(KINH)。钢筋材料的屈服准侧和强化准则分别选用ANSYS中提供的Von.Mises准则和BKIN准则。

3) 钢筋与混凝土之间的黏结−滑移关系

在循环荷载作用下，随着桥墩墩顶位移的增加，钢筋和混凝土之间会产生一定的滑移。钢筋和混凝土之间的滑移关系对桥墩的承载力和滞回曲线的形状都有一定的影响，从Manfredi等[20−22]研究可以发现，考虑钢筋与混凝土之间的黏结−滑移关系后，桥墩的承载力会降低，滞回曲线的“捏缩”效应更加显著。本文选用理想弹塑性黏结−滑移本构模型[23]。

1.3 数值模拟结果与试验结果的对比分析

以2个桥墩的拟静力试验结果为依据，基于ANSYS有限元软件，选用上述本构关系，建立少筋混凝土重力式桥墩的滞回分析模型。数值模拟位移加载步长与拟静力试验实际加载时位移步长相同，得到桥墩的滞回曲线和骨架曲线，并与试验值进行对比，如图3和图4所示。

(a) 滞回曲线；(b) 骨架曲线

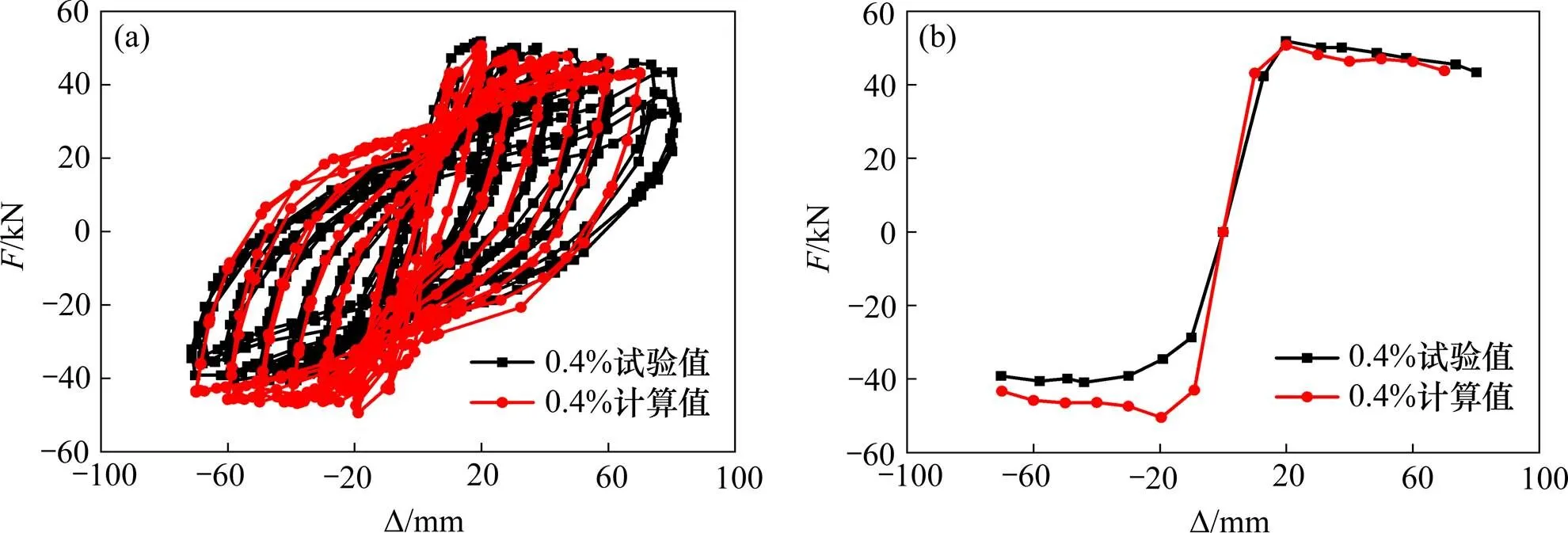
(a) 滞回曲线；(b) 骨架曲线

从图3和图4中的滞回曲线和骨架曲线对比可以看出，配筋率为0.3%的桥墩加载初期，随着加载位移的增大，桥墩的承载力越来越大，当承载力达到峰值后再增大加载位移，桥墩的承载力突然下降到峰值的0.85倍以下，失去承载能力，表现出了典型的脆性破坏特征；配筋率为0.4%的桥墩，在承载力达到最大之后缓慢下降，表现出了较好的延性性能。利用ANSYS模拟得到的结果与试验结果吻合较好，说明建立的滞回分析模型可用于少筋混凝土重力式桥墩的数值计算分析。

2 少筋混凝土重力式桥墩分析模型计算

为进一步探讨少筋混凝土重力式桥墩在拟静力作用下的抗震性能，本文采用上述建模方法分析剪跨比、轴压比和纵筋率等参数对少筋混凝土重力式桥墩延性系数、刚度退化和耗能性能的影响，具体桥墩设计参数见表1。模拟得到桥墩的滞回曲线和骨架曲线，见图5~6所示。

(a), (b) 配筋率0.3%的桥墩；(c), (d) 配筋率0.4%的桥墩

(a), (b) 配筋率0.3%的桥墩；(c), (d) 配筋率0.4%的桥墩

从图5和图6中可以看出：轴压比和剪跨比越大，桥墩的滞回曲线“捏拢”效应越严重；最大承载力随轴压比和配筋率的增大而增大，随剪跨比的增大而减小。由骨架曲线可以看出：桥墩屈服之前骨架曲线呈线性增长，屈服之后桥墩承载能力缓慢增长；加载后期随着剪跨比的减小和轴压比的增加，骨架曲线出现急速下降段，说明少筋混凝土重力式桥墩随剪跨比的减小和轴压比的增大脆性破坏特征越明显。

3 少筋混凝土重力式桥墩抗震性能的参数分析

3.1 轴压比对抗震性能的影响分析

3.1.1 位移延性系数

本文根据骨架曲线采用Park法[24]估算桥墩的屈服位移和极限位移，见图7。具体步骤如下：依据得到的骨架曲线，确定最大的侧向力max及骨架曲线上0.75max的点，连接原点与并延伸该线与最大侧向力max水平线交于点，其交点对应的位移即为屈服位移X，骨架曲线下降段对应的0.85max的位移即为极限位移X，则位移延性系数表示为：

表2列出了各桥墩的位移延性系数，从计算结果可知，少筋混凝土重力式桥墩的位移延性系数在3.0~4.7之间，小于钢筋混凝土桥墩的最小位移延性限值[25]。因此，在设计时钢筋混凝土桥墩的延性设计不能直接用于少筋混凝土重力式桥墩。

表2 位移延性系数计算

依据表2的计算结果具体分析轴压比对桥墩的位移延性系数的影响。图8给出了桥墩的位移延性系数随轴压比变化的曲线。

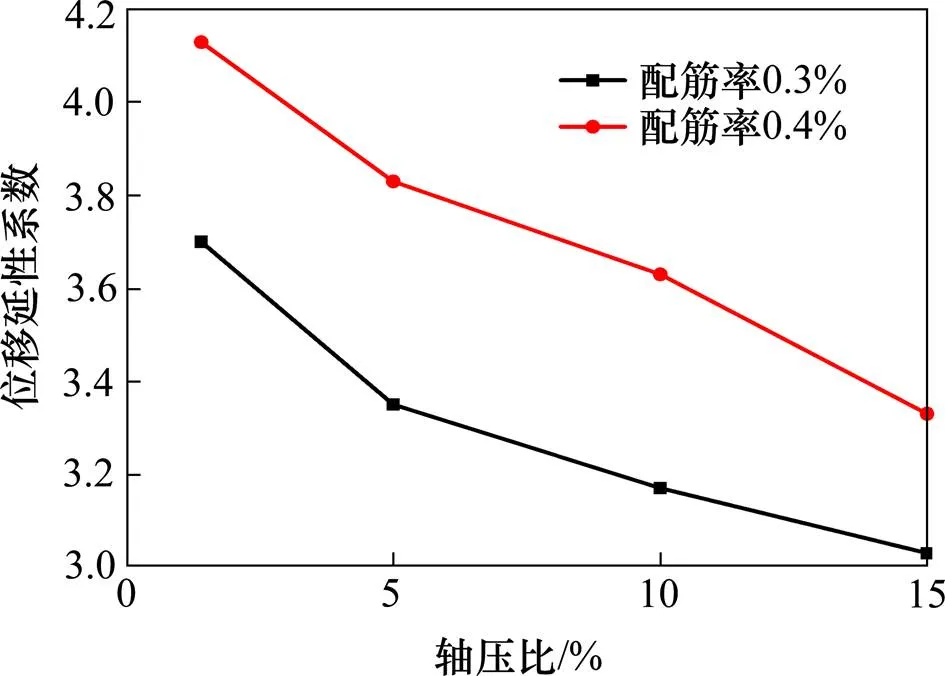
图8 位移延性系数随轴压比的变化图

从图8可以看出，随着轴压比的增大，桥墩的位移延性系数减小；轴压比小于5%时，位移延性系数减小速率较快，轴压比大于5%时，位移延性系数减小速率相对变缓。

3.12 刚度退化

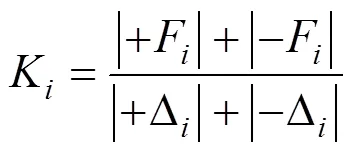
由图可以看出，加载初期桥墩的刚度较大，且下降速度很快。随着加载位移的增大，桥墩的刚度下降速度变慢。轴压比对桥墩的初始刚度有很大的影响，相同剪跨比下，轴压比越大初始刚度越大；随着轴压比的增大，桥墩破坏时刚度突然下降，呈现出典型的脆性破坏特征。

3.1.3 耗能能力

桥墩的耗能能力是指桥墩在地震力作用下发生塑性变形而吸收能量的能力，也是评价桥墩抗震性能的重要指标。工程抗震设计中一般采用累积滞回耗能和等效黏滞阻尼系数来定量的评定桥墩耗能能力的强弱[27]。根据文献[28]中的计算方法得到各桥墩的累积滞回耗能随位移变化的曲线，如图10所示。

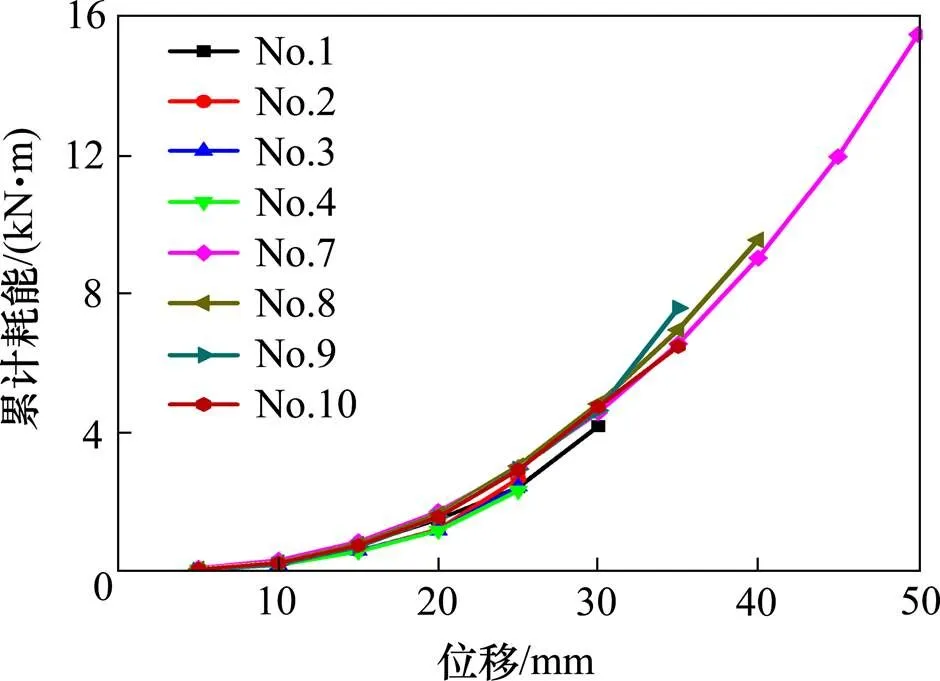
图10 不同轴压比累计耗能曲线图

图11 不同轴压比最大等效黏滞阻尼系数

由图可以看出，轴压比越小，桥墩的累积耗能能力越强，图11中各桥墩的最大等效黏滞阻尼系数变化曲线中能直观的反映这一规律；相同位移下，轴压比的大小对桥墩的累积耗能影响不大。

3.2 剪跨比对抗震性能的影响分析

3.2.1 位移延性系数

依据表2的计算结果具体分析剪跨比对桥墩的位移延性系数的影响。图12给出了桥墩的位移延性系数随剪跨比变化的曲线。

从图12可以看出，随着剪跨比的增大，桥墩的位移延性系数增大，且位移延性系数的增加速率受到配筋率的影响。

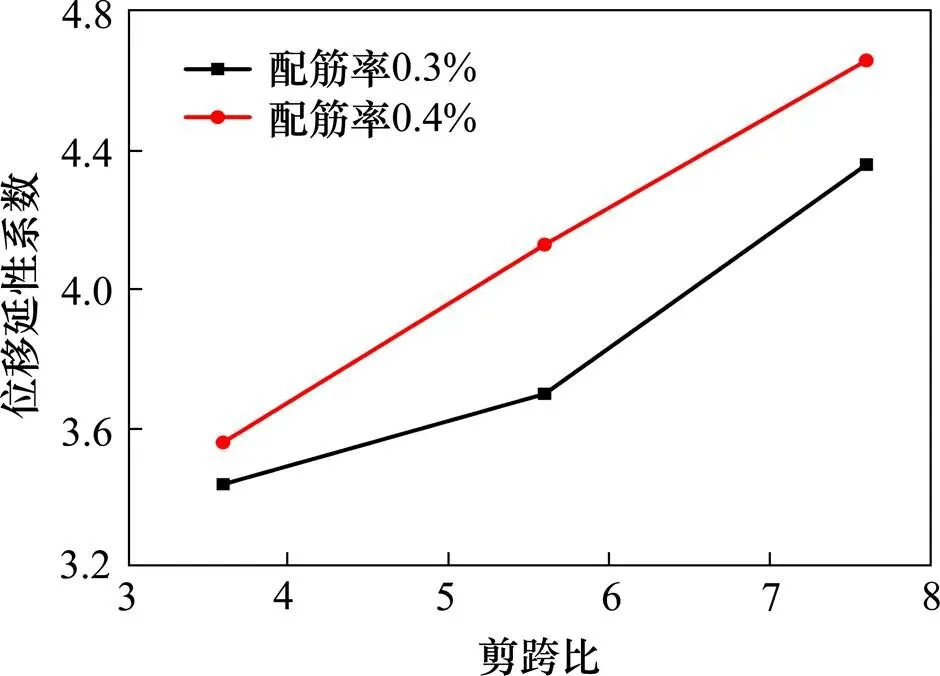
图12 位移延性系数随剪跨比的变化

3.2.2 刚度退化

依据式(2)计算得到不同剪跨比下桥墩的退化刚度曲线，见图13。

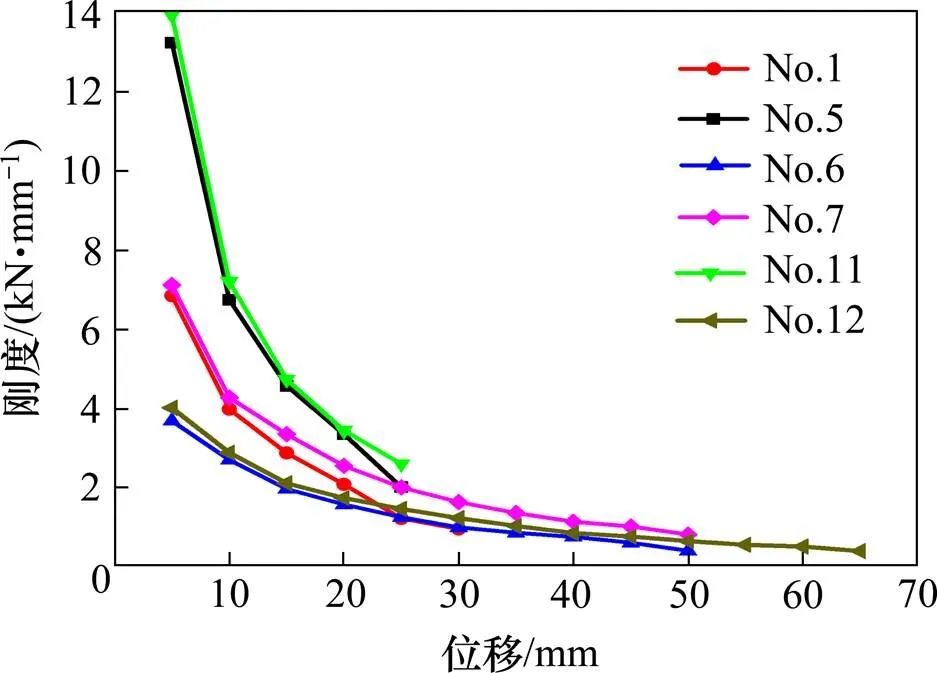
图13 不同剪跨比刚度退化曲线

由图可以看出，剪跨比越小，桥墩的初始刚度越大，且刚度下降速度越快；随着剪跨比的增加，桥墩的刚度退化速度减缓。

3.2.3 耗能能力

根据文献[28]中的计算方法得到各桥墩的不同剪跨比下累积滞回耗能随位移变化的曲线，如图14。

由图14可以看出，剪跨比对桥墩的累积耗能有显著的影响，配筋率为0.4%的桥墩，累积耗能随剪跨比的增大而增多，配筋率为0.3%的桥墩却表现出不同的变化规律，累积耗能随剪跨比的增大先减小后增多，这一规律与图15中最大等效黏滞阻尼系数变化规律相同，对于少筋混凝土结构而言，剪跨比对桥墩的累积耗能的影响规律受配筋率的影响；相同位移下，剪跨比越小桥墩的累积耗能就 越多。

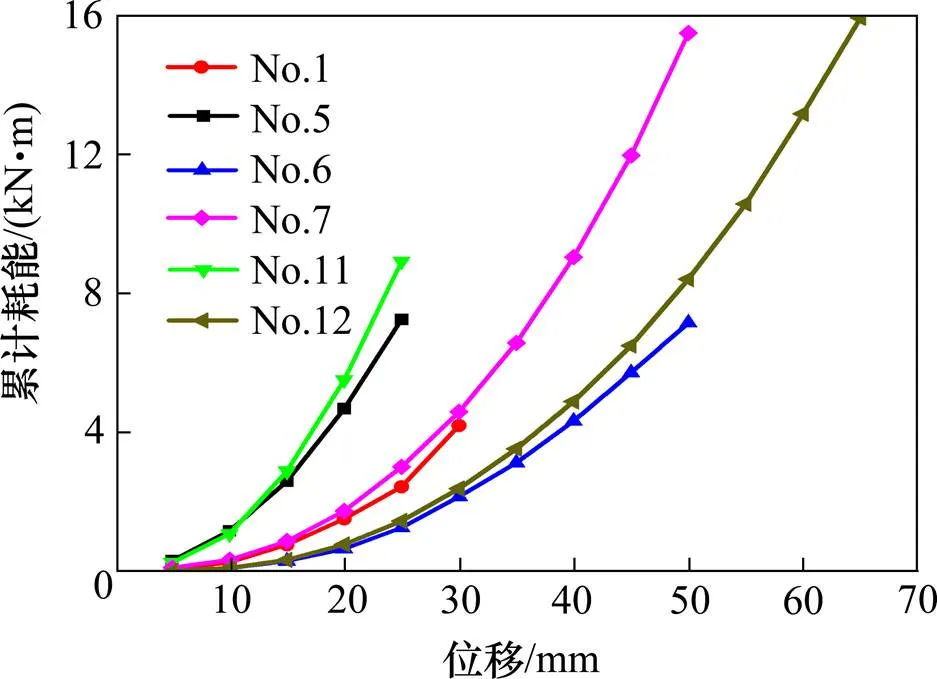
图14 不同剪跨比累计耗能曲线图

图15 不同剪跨比最大等效黏滞阻尼系数

3.3 配筋率对抗震性能的影响分析

3.3.1 位移延性系数

由图8和图12可以看出，当轴压比和剪跨比保持不变时，随着纵筋率的增大，桥墩的位移延性系数增加。剪跨比较小时，随着配筋率的增加，桥墩的位移延性系数增加较小；剪跨比较大时，随着配筋率的增加，桥墩的位移延性系数增加较大。

3.3.2 刚度退化

从图9和图13中各桥墩的刚度退化曲线可以看出，随着配筋率的增加，桥墩的刚度有所增大，且刚度退化速度变缓，说明提高桥墩的配筋率可以增强桥墩的刚度同时还可以提高桥墩抵抗地震的能力。

3.3.3 耗能能力

由图10和图14可以看出，配筋率对桥墩的累积耗能有很大的影响，随着配筋率的增加，桥墩的极限位移增大，消耗的能量越多；相同位移下，配筋率越高，桥墩累积耗能越多。

4 结论

1) 试验结果表明配筋率对桥墩的延性性能有很大的影响，配筋率越低桥墩表现出来的脆性破坏越明显。

2) 轴压比越大，桥墩表现出脆性破坏特征越明显，而且随着轴压比的增加，桥墩的刚度退化速率加快，延性性能及耗能能力减弱。

3) 剪跨比对桥墩的抗震性能有着显著的影响，随着剪跨比的增加桥墩的刚度退化速率减慢，延性性能增强，但是耗能能力受到配筋率的影响，配筋率较低时耗能能力呈现出先减小后增加的趋势。

4) 少筋混凝土重力式桥墩增大配筋率可以显著提高桥墩的抗震能力。

5) 少筋混凝土重力式桥墩由于其配筋率较低，延性性能不足。

[1] 孙树礼. 高速铁路桥梁设计与实践[M]. 北京: 中国铁道出版社, 2011. SUN Shuli. Design and practice of high speed railway bridges[M]. Beijing: China Railway Press, 2011.

[2] 徐勇, 金福海, 杨福泰, 等. 武广铁路客运专线四院范围桥梁总体设计[J]. 铁道标准设计, 2010(1): 94−99. XU Yong, JIN Fuhai, YANG Futai, et al. The overall design of the bridge in the Four Institute of Wu-Guang railway passenger dedicated line[J]. Railway Standard Design, 2010(1): 94−99.

[3] 郑健. 中国高速铁路桥梁[M]. 北京: 高等教育出版社, 2008. ZHENG Jian. Chinese high-speed railway bridge[M]. Beijing: Higher Education Press, 2008.

[4] 鞠彦忠, 阎贵平, 刘林. 低配筋大比例尺圆端型桥墩抗震性能的试验研究[J]. 土木工程学报, 2003, 36(11): 65−69. JU Yanzhong, YAN Guiping, LIU Lin. Experimental study on seismic behaviors of large-scale RC round- ended piers with low reinforcement ratio[J]. China Civil Engineering Journal, 2003, 36(11): 65−69.

[5] 鞠彦忠, 阎贵平, 李永哲. 低配筋铁路桥墩抗震性能的试验研究[J]. 铁道学报, 2004, 26(5): 91−95. JU Yanzhong, YAN Guiping, LI Yongzhe. Experimental study on seismic behaviors of railway bridge piers with low reinforcement ratio[J]. Journal of the China Railway Society, 2004, 26(5): 91−95.

[6] 蒋丽忠, 邵光强, 姜静静, 等. 高速铁路圆端形实体桥墩抗震性能试验研究[J]. 土木工程学报, 2013(3): 86− 95.JIANG Lizhong, SHAO Guangqiang, JIANG Jingjing, et al. Experimental study on seismic performance of solid piers with round ended cross-section in high-speed railway[J]. China Civil Engineering Journal, 2013(3): 86−95.

[7] 姜静静. 高速铁路圆端型实心桥墩抗震性能研究[D]. 长沙: 中南大学, 2012. JIANG Jingjing. The study of seismic behavior on solid piers with round ended in high-speed railway[D]. Changsha: Central South University, 2012.

[8] 赵冠远, 张同越, 陈鑫. 低周反复荷载下高速铁路桥墩抗震试验研究[J]. 中国铁道科学, 2014, 35(4): 38−44. ZHAO Guanyuan, ZHANG Tongyue, CHEN Xin. Experimental study on the seismic performance of high speed railway bridge pier under low cyclic loading[J]. China Railway Science, 2014, 35(4): 38−44.

[9] 王欢. 配筋率对高速铁路圆端形实心桥墩地震响应影响研究[D]. 长沙: 中南大学, 2014. WANG Huan. Influence of reinforcement ratio on seismic response of round-ended bridge piers in high speed railway[D]. Changsha: Central South University, 2014.

[10] 周赞. 剪跨比对高速铁路圆端形实心桥墩地震响应的影响[D]. 长沙: 中南大学, 2014. ZHOU Zan. The influence of shear-span ration on the seismic response of round-ended solid piers in high speed railway[D]. Changsha: Central South University, 2014.

[11] 刘浩.少筋混凝土铁路桥墩的抗震性能研究[D]. 北京: 北京交通大学, 2010. LIU Hao. Numerical stimulation of rare-reinforced concrete railway bridge pier’s seismic behavior[D]. Beijing: Beijing Jiaotong University, 2010.

[12] 李霖. 低配筋率高速铁路桥墩抗震延性分析[D]. 北京:北京交通大学, 2017. LI Lin. Ductility seismic analysis of high-speed railway bridge piers with low reinforcement ratio[D]. Beijing: Beijing Jiaotong University, 2017.

[13] 张永亮, 陈兴冲, 丁明波, 等. 多遇地震下少筋混凝土重力式桥墩验算指标研究[J]. 铁道工程学报, 2014(11): 72−76. ZHANG Yongliang, CHEN Xingchong, DING Mingbo, et al. Research on checking indexes of concrete gravity piers with low longitudinal reinforcement ratio under a low-level earthquake[J]. Journal of Railway Engineering Society, 2014(11): 72−76.

[14] 陈兴冲, 张永亮, 丁明波, 等. 少筋混凝土重力式桥墩抗震设计方法研究[J]. 铁道工程学报, 2016(3): 76−80. CHEN Xingchong, ZHANG Yongliang, DING Mingbo, et al. Research on seismic design method for concrete gravity piers with low longitudinal reinforcement ratio[J]. Journal of Railway Engineering Society, 2016(3): 76−80.

[15] 陈兴冲, 张永亮, 丁明波, 等. 罕遇地震下少筋混凝土重力式桥墩最低配筋率研究[J]. 桥梁建设, 2016, 46(5): 24−28. CHEN Xingchong, ZHANG Yongliang, Ding Mingbo, et al. Study of minimum reinforcement ratios for concrete piers arranged with small amount of reinforcement under rare earthquake[J]. Bridge Construction, 2016, 45(5): 24− 28.

[16] Mander J B, Priestley M J N, Park R. The theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804−1826.

[17] Dodd L L, Restrepo-Posada J I. Model of predicting cyclic behavior of reinforcing steel[J]. Journal of Structural Engineering, ASCE, 1995, 121(3): 433−445.

[18] Faria R, Pouca N V, Delgado R. Simulation of the cyclic behavior of R/C rectangular hollow section bridge piers via a detailed numerical model[J]. Journal of Earthquake Engineering, 2004, 8(5): 725−748.

[19] 司炳君, 孙治国, 艾庆华, 等. 钢筋混凝土桥墩滞回性能的有限元参数敏感性分析及模型改进[J]. 工程力学, 2009, 26(1): 174−180, 186. SI Bingjun, SUN Zhiguo, AI Qinghua, et al. Sensitive analysis and model modification for finite element analysis of R/C bridge piers under cyclic loading[J]. Engineering Mechanics, 2009, 26(1): 174−180, 186.

[20] Manfredi G, Pecce M. A refined RC beam element including bond-slip relationship for the analysis of continuous beams[J]. Computers and Structures, 1998, 69: 53−62.

[21] Youssef M, Ghobarah A. Strength deterioration due to bond slip and concrete crushing in modeling of reinforced concrete members[J]. ACI Structural Journal, 1999, 96(6): 56−66

[22] Casanova A, Jason L, Davenne L. Bond slip model for the simulation of reinforced concrete structures[J]. Engineering Structures, 2012, 39: 66–78.

[23] Han T S, Peter H F, Billington S L. Simulation of highly ductile fiber-reinforced cement-based composite components under cyclic loading[J]. ACI Structural Journal, 2003, 100(6): 749−757.

[24] Park R. Evaluation of ductility of structures and structural assemblages from laboratory testing[J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1989, 22(3): 155−166.

[25] GB50111—2006, 铁路工程抗震设计规范[S]. GB50111—2006, Code for seismic design of railway engineering[S].

[26] JGJ 101—96, 建筑抗震试验方法规程[S]. JGJ 101—96, Specification of test methods for earthquake resistant building[S].

[27] 田甜, 邱文亮, 齐中新,等. 剪跨比对钢管混凝土组合桥墩抗震性能影响试验研究[J]. 大连理工大学学报, 2017, 57(2): 133−141. TIAN Tian, QIU Wenliang, QI Zhongxin, et al. Experimental study for effects of shear span ratio on seismic performance of concrete filled steel tube (CFTS) composite bridge columns[J]. Journal of Dalian University of Technology, 2017, 57(2): 133−141.

[28] 葛继平. 节段拼装桥墩抗震性能试验研究与理论分析[D]. 上海: 同济大学, 2008. GE Jiping. Experimental study and theoretical analysis of seismic behavior of segmental assembled piers[D]. Shanghai: Tongji University, 2008.

Seismic performance analysis of railway gravity piers with low longitudinal reinforcement ratio

LU Jinhua, CHEN Xingchong, DING Mingbo, ZHANG Xiyin

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

A finite element model for hysteretic analysis of railway gravity piers with low longitudinal reinforcement ratio was established, compared with the pseudo-static test results of two piers with bending failure. The seismic behavior of gravity piers was studied. The influences of shear span ratio, axial compression ratio and reinforcement ratio on displacement ductility, stiffness degradation and energy dissipation capacity of piers were discussed. It was found that the stiffness degradation rate of piers was faster, the ductility performance was smaller and the energy dissipation capacity was weaker, with the increase of axial compression ratio. The increase of shear span ratio would slow down the rate of stiffness degradation and enhance ductility performance of bridge piers, but the energy dissipation capacity was greatly affected by the longitudinal reinforcement ratio. The lower the longitudinal reinforcement ratio of the pier was, the more obvious the influence was. In addition, increasing the longitudinal reinforcement ratio could significantly improve the seismic capacity of bridge piers. When the gravity pier with few reinforcement concrete was damaged, it presented brittle failure characteristics and weak ductility performance.

low reinforcement ratio; gravity railway pier; numerical simulation; seismic performance

U24

A

1672 − 7029(2019)09−2223 − 10

10.19713/j.cnki.43−1423/u.2019.09.013

2018−11−20

国家自然科学基金资助项目(51768036，51808273)

丁明波(1975−)，男，山东日照人，副教授，博士，从事桥梁抗震方面研究；E−mail：ding_mingbo@126.com

(编辑 涂鹏)