基于土体软化规律的双折减系数法研究

张飞雷，苏永华，郭立毅

基于土体软化规律的双折减系数法研究

张飞雷，苏永华，郭立毅

(湖南大学 土木工程学院，湖南 长沙 410082)

双折减系数法(DRM)在边坡稳定性评估中正逐渐得到广泛应用，但是在计算过程中强度参数的折减规律以及2个折减系数之间的关系值得进一步探讨。基于边坡临界强度参数曲线和初始强度参数，以正切角的概念推导折减比例公式，分析其几何意义以及物理意义。依据算例结果，探讨折减比例与强度参数折减路径的关系。以土体材料强度参数遵循线性软化衰减规律，推导内摩擦角与黏聚力的函数关系式，将关系式引入经典强度折减法，提出一种基于土体软化规律的双折减系数法。算例表明，该方法在计算中充分考虑了岩土体材料本身强度参数衰减规律，计算过程更加符合实际情况。

双折减系数法；临界强度参数曲线；折减比例；土体软化规律

英国学者Zienkiewicz[1]于1975年提出并开始使用强度折减法(SRM - strength reduction method)。该方法中强度参数黏聚力和内摩擦角按照同一比例进行折减，直至达到极限平衡状态，将此状态下的折减系数定义为边坡的安全系数。SRM由于考虑了岩土体材料的本构关系、不用假定滑移面等优势而得到了广泛的应用[2]。该理论默认的前提是强度参数指标黏聚力与内摩擦角具有相同的安全储备。在实际情况中，边坡从稳定到破坏的过程中受到多种因素(人工活动、地震和水等)的影响，岩土体材料的强度参数指标和发挥着不同的作用[3]。同时研究发现，边坡在破坏发展的过程中，强度参数黏聚力和内摩擦角的弱化速率、弱化程度、发挥的作用及作用的顺序也不相同[4−8]。在考虑以上影响因素进行边坡稳定性分析时，研究学者开始对强度参数选用不同的折减系数来反映这种现象，并由此产生双折减系数法(DRM-double strength reduction method)。对于双折减系数法，国内的唐芬等[4−6]最早对该方法进行研究，并通过人为假定强度参数折减比例的方式来反映强度参数指标不同的作用顺序及衰减速率。JIANG等[7]通过研究则建议采用折减比例为1.75对均质土坡进行计算。YUAN等[8]通过数据拟合的方式，通过坡角确定参数的折减比例，由此确定相应的折减原则。朱彦鹏等[9−10]通过获得单独折减强度参数的方式确定折减比例值。Isakov等[11]指出，上述预先确定折减比例的方式无理论依据，强度参数和在不同的影响因素下没有唯一确定的函数关系。薛海斌等[12−13]在强度参数服从线性软化规律的前提假定下，经过公式推导确定黏聚力和内摩擦角折减系数的函数关系，进而提出一种非等比例的双安全系数法。从上述研究可以发现，由于采用了2个折减系数，如何合理的对强度参数进行折减成为亟待探讨的问题。基于上述问题，本文在前人的基础上，首先以临界参数曲线与临界强度参数为基础，基于正切角的概念推导折减比例公式，对其物理意义几何意义进行解释；然后基于线性应变软化模型，确定强度参数的函数关系式，并将此关系式引入经典强度折减法，在此基础上对强度参数进行折减，提出一种基于土体软化规律的双强度折减法。最后通过具体算例，验证本文方法的优越性及合理性。

1 双折减系数法

1.1 双折减系数的定义

在Mohr-Coulomb强度准则下，土体的抗剪强度可以表示为：

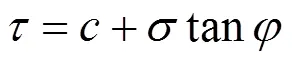
式中：为滑裂面上的原始剪应力状态；为滑裂面上原始正应力状态；和为初始抗剪强度参数。

SRM的实质是以边坡土体的初始抗剪强度为基准，通过对其不断的折减，直至边坡处于临界破坏状态，此时土体的临界抗剪强度为，定义折减系数即为边坡安全系数。这个不断的折减过程，在坐标系中可以解释为对初始Mohr- Coulomb强度曲线的不断移摆以获得一条截距为/，倾角为/的直线的过程。

土体内部应力−应变关系十分复杂，强度参数指标和真实的变化规律及其具体的耦合关系很难得到准确的描述。根据潘家铮提出的最大值原理[14]可以肯定的是：在外部环境因素的(如人类活动、地震和水等)影响下，强度参数指标和之间存在某种特定关系，在这种关系下，强度参数指标和可以共同作用使土体抵抗外部影响的反力达到最大。

在实际研究中，边坡在渐进失稳直至破坏的过程中，土体的强度参数和发挥着不同的作用，出现不同程度的衰减，两者对应的安全储备也是不同的。因此在采用强度折减法进行稳定性分析时，和应该对应于不同折减系数值，即应采用双折减系数进行分析。

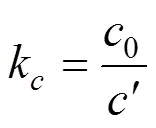
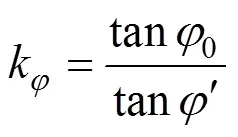
式中：0和0为土体的初始强度参数；和为临界状态时强度参数。

1.2 折减比例的推导

袁维等[15]通过数值模拟分析计算，发现对于一个几何结构和岩土体重度一定的边坡而言，由黏聚力和内摩擦角组合而成的临界强度参数曲线是一定的，可以用双曲线来描述。

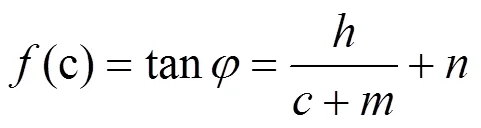
式中：h，m和n为待定常数。

在抗剪强度参数的折减过程中，抗剪强度参数沿某一路径折减至临界状态，并且要保持这一路径，折减系数k和k需要按照一定关联确定，这种关联在以往的研究中，通常采用折减比例来表示：

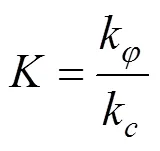
根据图1中各曲线的几何关系，可得：

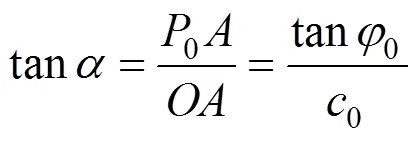
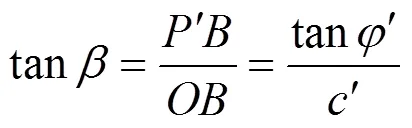
将式(2)和(3)代入式(7)，有：

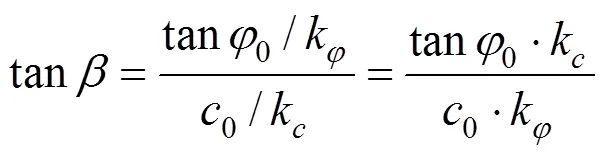
联立式(6)和(8)可得：

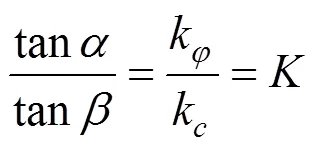
式中：k和k为抗剪强度参数折减系数。

通过上述公式的推导，可以得出折减比例值在几何意义上可以定义为角和角正切值的比值。在强度参数坐标系中，考虑强度参数的折减时，可以对黏聚力和内摩擦角的折减程度(安全储备)进行很好的描述。当1时，强度参数的折减系数相等，=，折减路径方向为0→方向，内摩擦角与黏聚力的折减程度相同，这实际上就是传统强度折减法，是双折减系数法的一种特殊形式；当1时，折减路径位于0的下方，内摩擦角的折减程度大于黏聚力的折减程度；当<1时，折减路径位于0的上方，内摩擦角的折减程度小于黏聚力的折减程度。

1.3 折减路径

折减路径反映边坡破坏发展的机制，反映强度参数衰减的过程，折减路径的方向性体现强度参数发挥作用的顺序，路径的长短则体现了折减的程度，折减路径的量化表示即为折减比例值。

由图1可以看出，在强度参数坐标系中，强度参数的折减路径有很多种方式可以得到临界强度参数值，srm只是达到边坡临界状态的一种方式，是一条通过原点的直线。基于折减比例的DRM与SRM都是采用线性折减的方式来进行的，两者的主要差异体现在，折减比例值存在的目的是使抗剪强度参数和沿着最优的路径进行折减，使土体的抗力达到最大。值的不同直接导致折减路径发生改变，从而得到不同的临界强度参数值。因此在确定值之前应当首先确定强度参数的折减路径，而这条路径应当是更接近真实状态的。

下边将结合具体边坡算例讨论下述问题：假定抗剪强度参数和的折减系数的折减比例为，探讨预先设定的折减比例与折减路径的关系。边坡算例相关参数信息如下表1，由此计算得到强度参数折减比例与折减路径关系如图2所示。

表1 边坡算例参数

通过朱彦鹏等[10]对DRM折减范围的研究，针对本算例当折减比例值在[0.6，1.4]范围内，计算结果是可以接受的。

在图2中，仅取折减比例=1(SRM)与=0.83 (DRM)进行计算分析，可以看出两者仅在折减计算过程中的第一步处会有较大的区别，在之后的计算过程中都是在沿着固定斜率的直线在进行。这种情况的出现是因为在计算之前预先设定了折减系数的比例关系，其实质上是确定了黏聚力和内摩擦角的相对安全储备，在这种条件下使其以某种假定的衰减方式进行，然而这种方式与实际情况下强度参数的衰减方式并不一定相同。

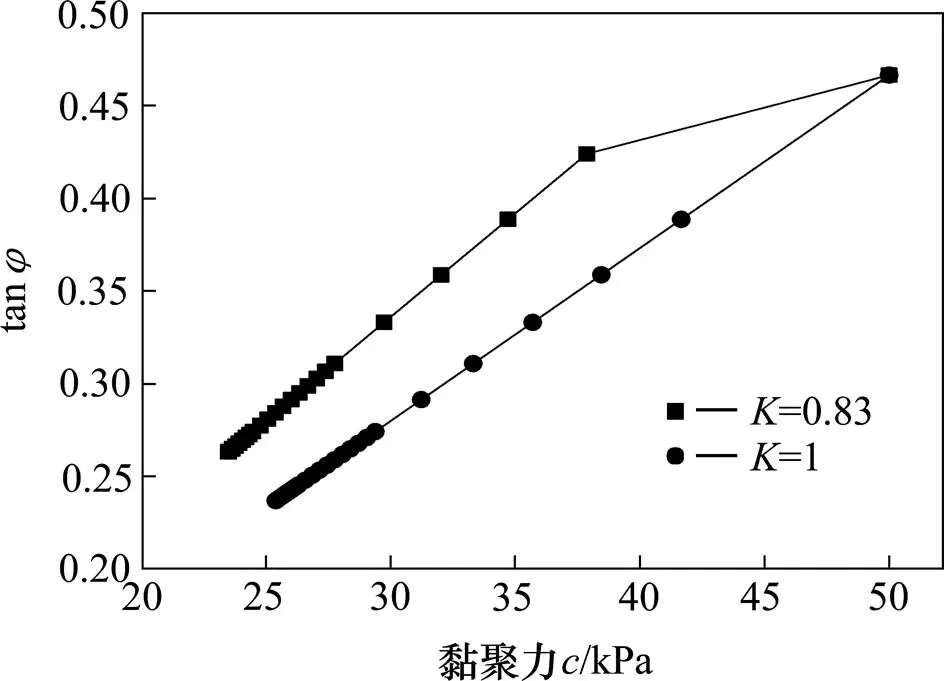
图2 折减比例(K)对折减路径的影响

通过上述的分析研究，折减比例的确定是强度折减法的关键，折减比例会影响折减路径，从而得到不同的临界强度参数。在采用强度折减法时，不同因素影响下的边坡，在折减过程中其强度参数指标和之间不存在唯一确定的比例关系。通过某种方式预先确定折减比例对强度参数进行折减的方式对强度参数的折减路径进行了限定，也很难给出合理的解释。通过对折减比例K 的推导，在获得临界参数后推导的折减比例可以对强度参数的折减程度进行很好的说明，建议取折减比例值仅用来反映强度参数指标间不同的折减程度。

2 基于应变软化规律的折减机制

2.1 岩土体材料强度参数软化规律

对于实际岩土体，在自然状态下会受到不同因素的影响，强度参数的衰减路径反映到强度参数坐标系中不一定是直线。在采用强度折减法进行稳定性分析时需要寻找符合实际情况的衰减路径。

对于应变软化岩土体，强度参数指标和随着塑性应变的发展而变化。因此在采用强度折减法时，强度参数随塑性应变的变化速率也应该反映在强度折减的路径上，这里采用flac3d中土体材料简单的线性软化模型[16]，如图3所示。

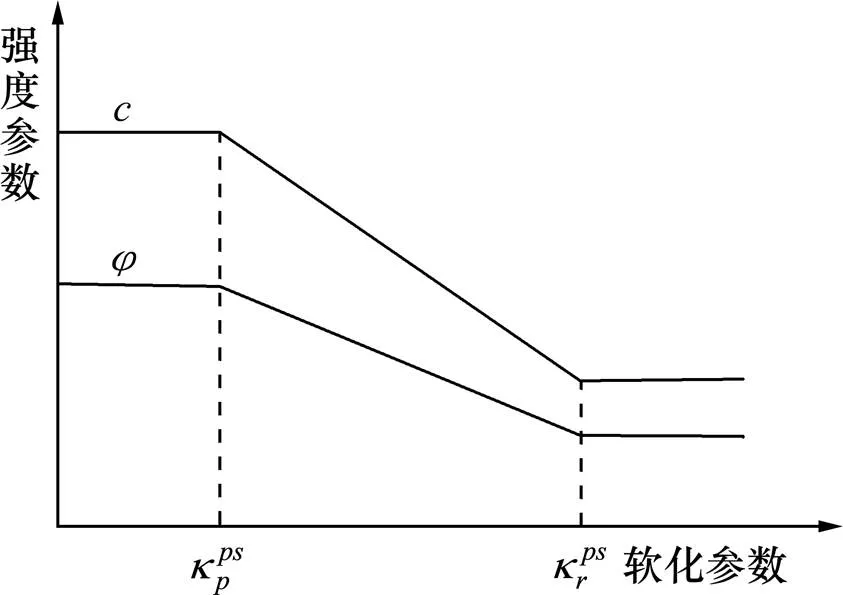
图3 应变软化模型

其中简化后软化参数的表达式如下：

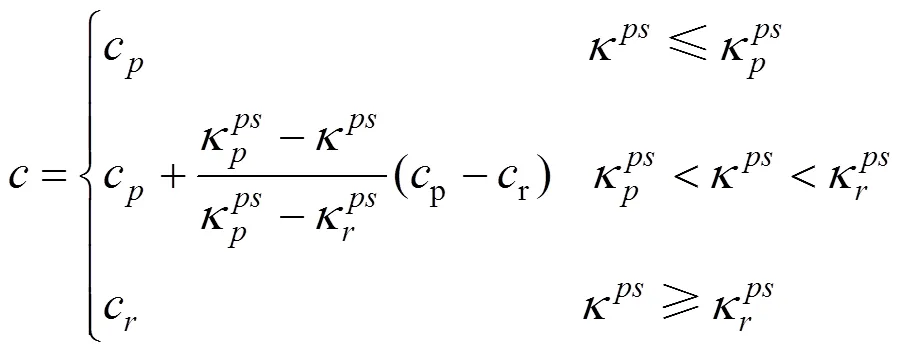
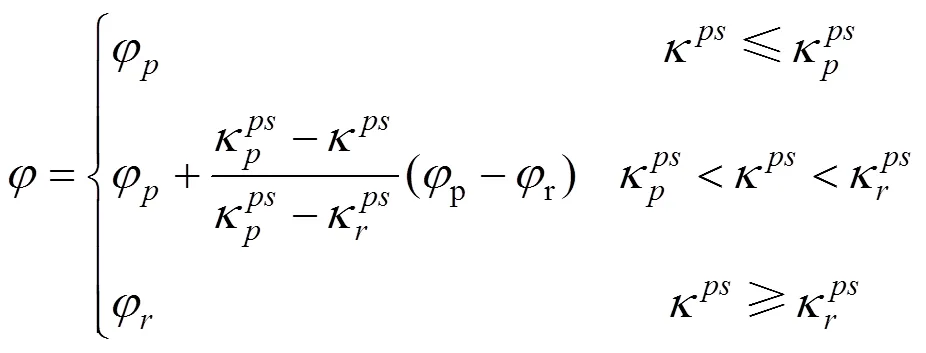
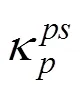
2.2 强度参数衰减关系

基于本文的研究思路，在采用双折减系数法时使计算过程沿着强度参数的真实衰减路径进行折减，需要得到强度参数指标和之间的的函数关系式，可以用下式进行表示。

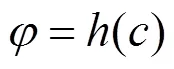
考虑到强度参数影响因素的随机性，如果通过实验或者其他手段得到边坡岩土体材料强度参数的衰减演化过程，应当予以采用。下面主要采用土体的应变软化模型来表达双折减系数法的思路。对应变软化模型公式中的软化阶段进行分析，由式(9)移项变换可得：

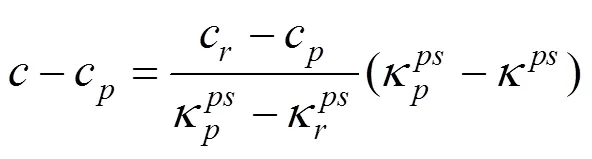
等式两边同除，得：

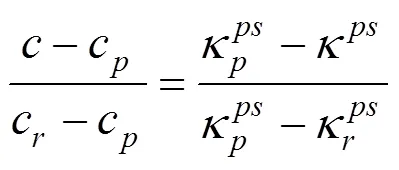
同理，对(10)变换：

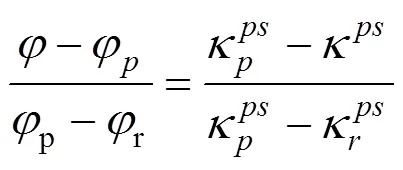
联立式(13)和(14)可得：

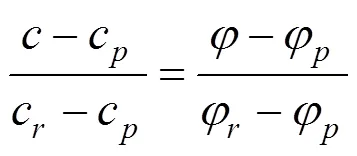
由式(15)可确定和的关系：

对应在tan坐标系中的公式为：

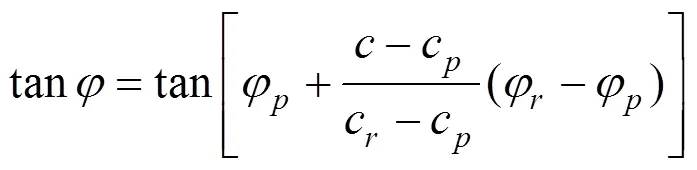
在数值计算中，参数赋值时直接赋予内摩擦角数值，衰减关系公式为：

2.3 折减方案及实现步骤

以3.2节线性应变软化阶段推导得到强度参数的衰减函数关系作为强度参数指标的折减路径，在其确定方式上保证了曲线可以经过真实的峰值强度和残余强度状态。以此作为折减路径进行计算，不断调整黏聚力的折减系数，而内摩擦角的折减系数由计算结果推导得出，基于此得到的极限状态的临界强度参数值是强度参数衰减路径上的值，其最终折减系数确定的参数安全储备更能反映实际情况。

在考虑应变软化衰减路径后，在flac3D计算中双折减系数法的程序实现构架如图4，具体的实现流程如下：

1) 建立边坡模型，设置初始条件，输入模型基本参数；

3) 确定折减路径，即确定强度参数的关系式；

4) 对黏聚力进行第一次折减，内摩擦角按照衰减路径随之变化，并记录折减系数及特征点位移；

5) 进行条件判断，重复第(4)步过程，直至 结束；

6) 计算完成，绘制位移曲线。

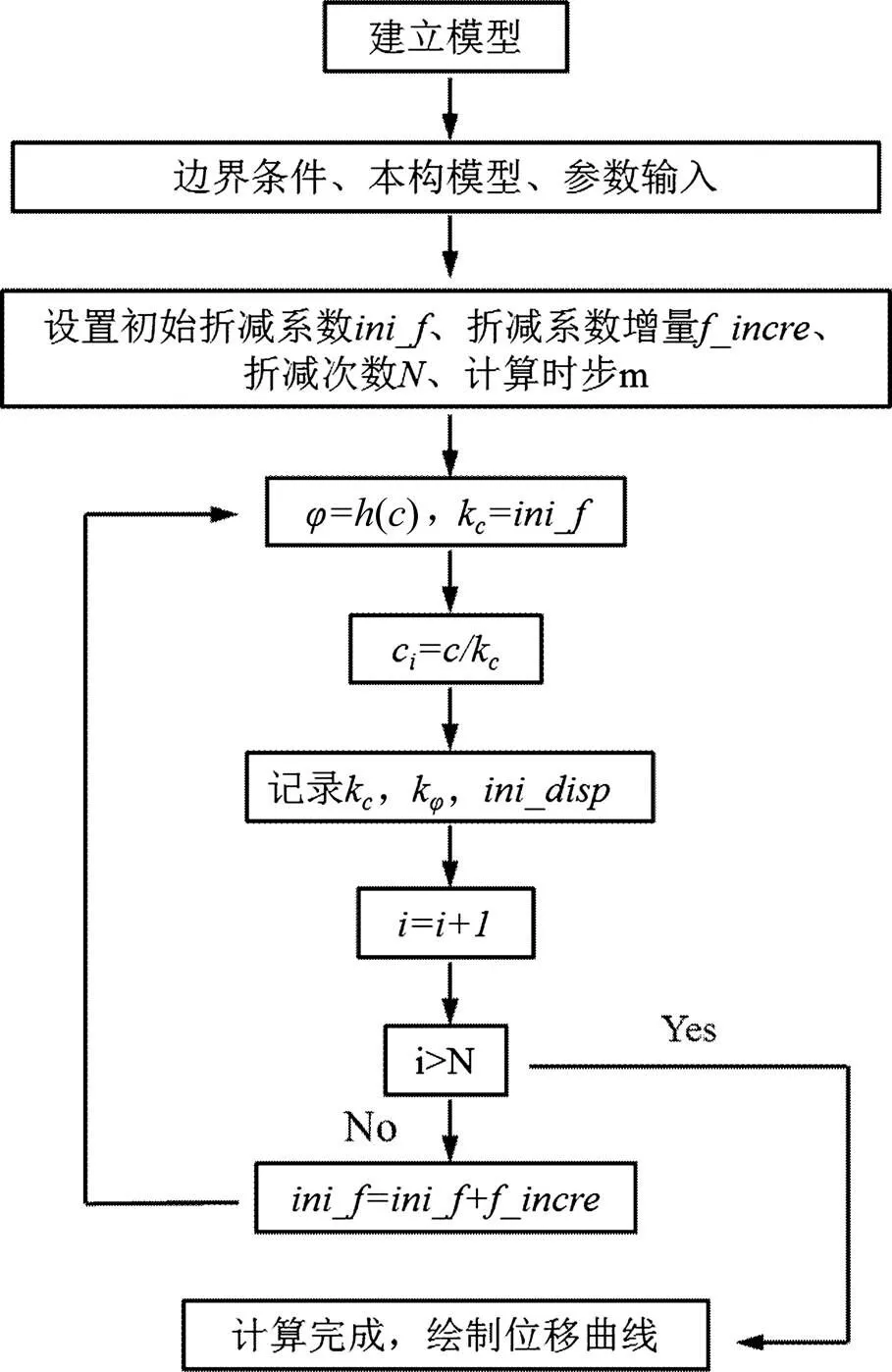
图4 双强度折减程序图

3 算例验证及分析

3.1 计算模型及参数

某各向同性均质边坡[13]，分析模型及形状如图5所示，材料参数如表2，其坡体材料具有应变软化特性，特征点选择坡顶A点。

根据上述材料参数，通过计算可得强度参数衰减关系公式为：

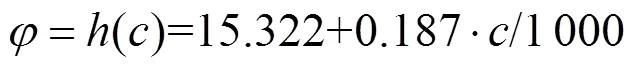
3.2 计算过程

根据节3.3计算步骤，进行计算，具体设置 如下：

1) 建立数值计算模型，选择M-C本构模型，左右边界水平约束，下部固定；

博物馆本身就一个品牌，在场馆内具有各种丰富的珍藏品，这些珍藏品都具有非常深厚的珍贵性，不得不说，这些珍藏品都是中华文化的瑰宝。对于博物馆来说，其产品必定具有其独特性，并且还将以珍贵度为基础，形成博物馆本身独有的文化创意品牌文化，通过将创意和科技融入到博物馆的文化产品中，使珍藏品的珍贵性和浓厚的历史文化，通过文化产品发挥其升值的社会效益以及树立浓厚的品牌文化。另外，通过各种营销方式使文化产品形成独特鲜明的品牌，让人们对博物馆的文化品牌具有更深的认识，使博物馆在受众中树立良好的品牌形象。

2) 设置初始折减系数=1.31=0.02(增量值前部)，2=0.005(增量值后部)，折减次数=25；

3) 输入式(20)，设置黏聚力的折减系数k=;

4) 开始计算，并记录折减系数k及特征点水平位移_。

5) 输出数据结果，并整理。

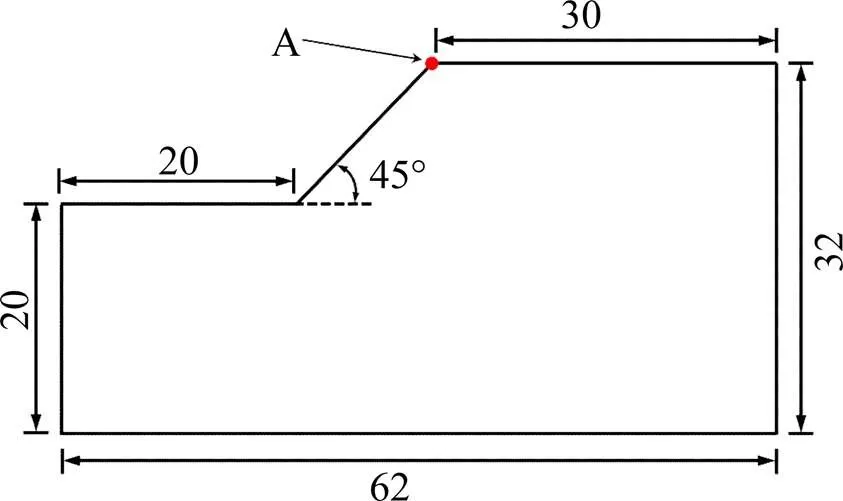
单位：m

表2 边坡土体参数

3.3 计算结果分析

折减过程中2折减系数间的关系以及强度参数指标的变化关系如图6所示。

从图6()中可以看出，在考虑土体的应变软化特征后，折减系数间的关系呈一条凸曲线，并非是完全的直线关系，反映出来的折减比例也并非是一个定值。这样的折减过程符合土体材料的强度参数的实际衰减过程，也可以很好的反映强度参数指标间不同的衰减速度。

而在图6(b)中，对折减过程中强度参数指标的变化进行拟合，可以发现拟合公式与公式(21)相同。在折减过程中强度参数指标的折减路径严格按照参数的衰减路径，得到的极限状态下的强度参数为边坡在破坏过程中土体强度参数衰减路径上的点，符合此边坡土体材料在实际状况中的应变软化特性。

为了进一步验证此方法的合理性，绘制特征监测点A的水平位移随折减系数变化曲线，如图7 所示。

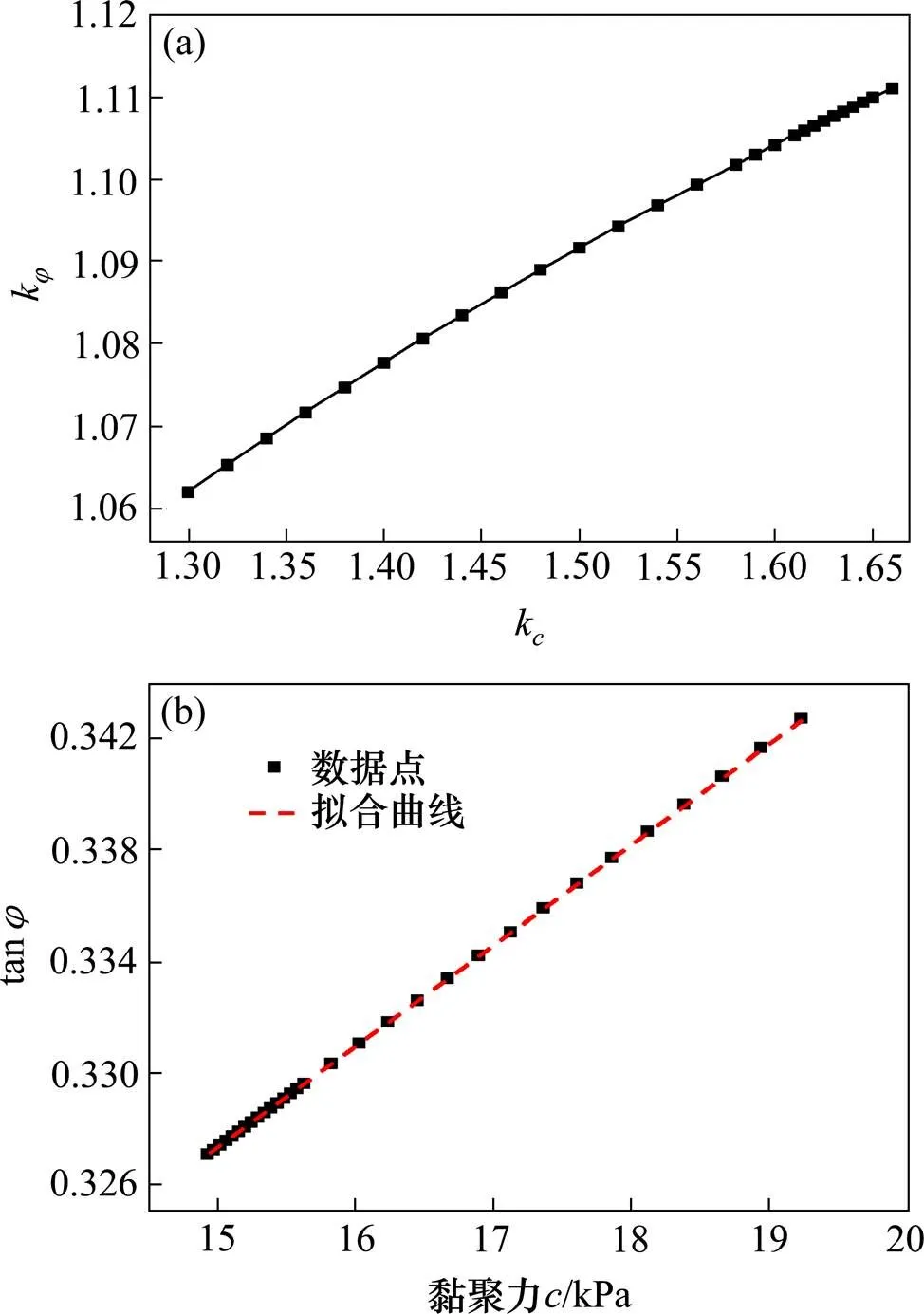
(a) kc和kp的关系；(b) 黏聚力的c和ptanφ的关系

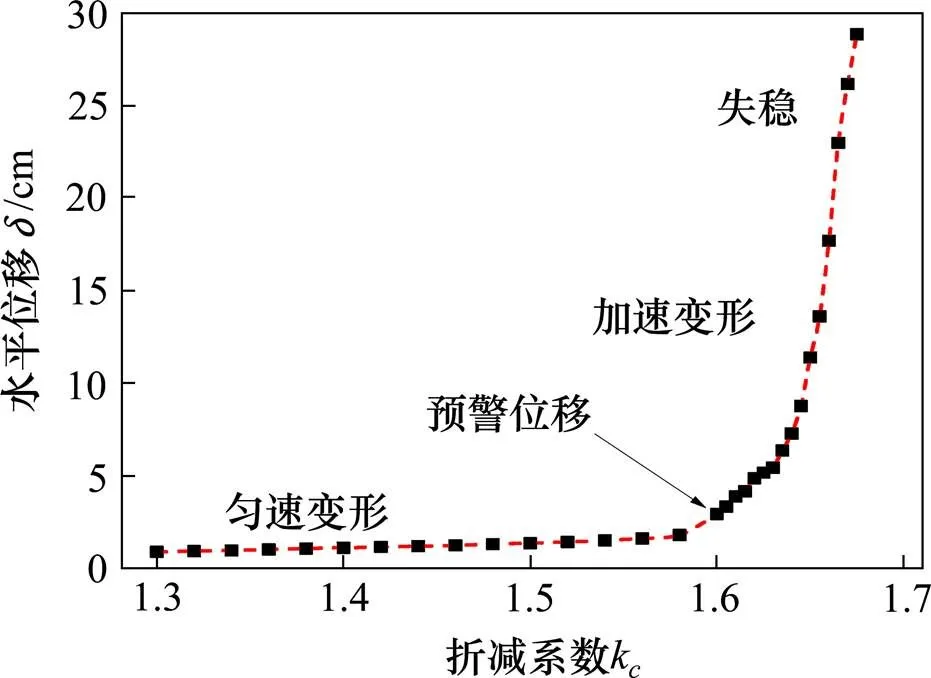
图7 折减系数kc与水平位移关系

曲线前段为损伤发展区，表现为匀速变形；之后进入位移突变区，表现为加速变形；突变区位移值可以作为预警参考值，这在边坡预测方面具有参考价值，突变区之后损伤贯通，边坡失稳破坏。

对折减系数−位移曲线进行双曲线拟合，选择双曲线方程[17]如下：

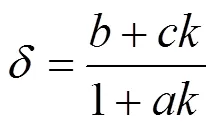
式中：，和为待定系数；为位移值；k为折减系数。

拟合结果为=−0.591 5，=−1.278 6，0.937 8。

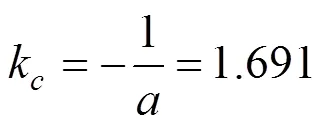
折减之后黏聚力及内摩擦角：

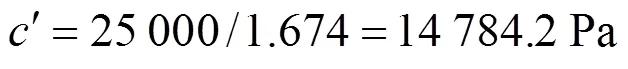
′=18.087° (24)

代入式(3)和(5)求得：

k=tan20°/tan18.087°=1.114 (25)

=1.114/1.691=0.658 8 (26)

从折减比例可以判断黏聚力的折减程度大于内摩擦角的折减程度，这也符合强度参数的峰值强度和残余强度的取值规律。

4 结论

1) 基于正切角概念推导了强度参数折减系数的比例关系式，在其确定方式上考虑了强度参数的真实的衰减路径，更能反映强度参数的安全储备情况。

2) 折减比例是一个和初始状态与最终状态有关的状态量，而与强度参数的折减过程无关，建议取折减比例仅反映强度参数衰减程度。

3) 以岩土体线性软化规律为基础，建立强度参数之间的衰减函数关系，并以此作为折减路径得到的极限状态更具有说服力。

4) 提出一种基于材料软化规律的双折减系数法，并通过简单算例与传统有限元强度折减法对比分析，验证本文方法的合理性。

[1] Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticityin soil mechanics[J]. Geotechnique, 1975, 25(4): 671−689.

[2] 郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381−3388. ZHENG Yingren, ZHAO Shangyi. Application of strength reduction FEM in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381−3388.

[3] 赵炼恒, 曹景源, 唐高朋,等. 基于双强度折减策略的边坡稳定性分析方法探讨[J]. 岩土力学, 2014(10): 2977−2984. ZHAO Lianheng, CAO Jingyuan, TANG Gaopeng, et al. Discussion on slope stability analysis with double strength reduction technique[J]. Rock and Soil Mechanics, 2014, 35(10): 2977−2984.

[4] 唐芬, 郑颖人. 边坡渐进破坏双折减系数法的机理分析[J]. 地下空间与工程学报, 2008(3): 436−441, 464. TANG Fen, ZHENG Yingren. Mechanism analysis on dual reduction factors about the progressive failure of slope[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(3): 436−441, 464.

[5] 唐芬, 郑颖人. 边坡稳定安全储备的双折减系数推导[J]. 重庆交通大学学报(自然科学版), 2007(4): 95−100. TANG Fen, ZHENG Yingren. Analysis on safety reserve of slope with two strength reduction factor[J]. Journal of Chongqing Jiaotong University (Natural Science), 2007, 26(4): 95−100.

[6] 唐芬, 郑颖人, 赵尚毅. 土坡渐进破坏的双安全系数讨论[J]. 岩石力学与工程学报, 2007, 26(7): 1402−1407. TANG Fen, ZHENG Yingren, ZHAO Shangyi. Discussion on two safety factors for progressive failure of soil slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1402−1407.

[7] JIANG X, WANG Z, LIU L, et al. The determination of reduction ratio factor in homogeneous soil-slope with finite element double strength reduction method[J]. Open Civil Engineering Journal, 2013, 7(1): 205−209.

[8] YUAN Wei, BAI Bing, LI Xiaochun, et al. A strength reduction method based on double reduction parameters and its application[J]. Journal of Central South University, 2013, 20(9): 2555−2562.

[9] 朱彦鹏, 杨晓宇, 严锐鹏, 等. 双强度折减法的配套折减机制[J]. 兰州理工大学学报, 2017, 43(2): 121−126. ZHU Yanpeng, YANG Xiaoyu, YAN Ruipeng, et al. Matching reduction mechanism of double reduction method[J]. Rock and Soil Mechanics, 2017, 43(2): 121−126.

[10] 朱彦鹏, 杨晓宇, 马孝瑞, 等. 边坡稳定性分析双折减法的几个问题[J]. 岩土力学, 2018, 39(1): 331−338. ZHU Yanpeng, YANG Xiaoyu, MA Xiaorui, et al. Several questions of double reduction method for slope stability analysis[J]. Rock and Soil Mechanics, 2018, 39(1): 331−338.

[11] Isakov A, Moryachkov Y. Estimation of slope stability with using two-parameter criterion of stability[J]. International Journal of Geomechanics, 2013, 14(3): 613−324.

[12] 薛海斌, 党发宁, 尹小涛, 等. 基于强度储备的边坡非等比例双安全系数研究[J]. 岩土力学, 2016, 37(4): 929−934, 942. XUE Haibin, DANG Faning, YIN Xiaotao, et al. Research on non-proportional double safety factors of slope based on strength reserve[J]. Rock and Soil Mechanics, 2016, 37(4): 929−934, 942.

[13] 薛海斌, 党发宁, 尹小涛, 等. 边坡强度参数非等比例相关联折减法研究[J]. 岩石力学与工程学报, 2015, 34(增2): 4005−4012. XUE Haibin, DANG Faning, YIN Xiaotao, et al. Research on method of slop strength parameters non-proportional associated reduction[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(Suppl 2): 4005−4012.

[14] 潘家铮. 建筑物的抗滑稳定和滑坡分析[M]. 北京: 中国水利水电出版社, 1980. PAN Jiazheng. Analysis of anti-ship stability and landslide of buildings[M]. Beijing: China Water and Power Press, 1980.

[15] 袁维, 李小春, 王伟, 等. 一种双折减系数的强度折减法研究[J]. 岩土力学, 2016, 37(8): 2222−2230. YUAN Wei, LI Xiaochun, WANG Wei, et al. Study on strength reduction method based on double reduction parameters[J]. Rock and Soil Mechanics, 2016, 37(8): 2222−2230.

[16] Itasca Consulting Group, Inc. FLAC3D: Fast lagrangian analysis of continua in 3 dimensions theory and background[M]. Minneapolis: Itasca Consulting Group Inc., 2005.

[17] 林杭, 曹平, 李江腾, 等. 边坡临界失稳状态的判定标准[J]. 煤炭学报, 2008, 33(6): 643−647. LIN Hang, CAO Ping, LI Jiangteng, et al. The standards for critical failure state of slope[J]. Journal of China Coal Society, 2008, 33(6): 643−647.

Research on double reduction factors method based on soil softening law

ZHANG Feilei,SU Yonghua, gUO liyi

(College of Civil Engineering, Hunan University, Changsha 410082, China)

in the analysis of slope stability, the double reduction factors method (DRM) is gradually widely used. however, in the process of calculating, the reduction law of strength parameters and the relationship between the two reduction factors deserve to be further determined. Firstly, based on the critical strength parameter curve and initial strength parameter of slope, the reduced proportion formula was deduced with the concept of tangent angle, and its geometric and physical meanings were analyzed. then the relationship between the reduction ratio and the reduction path of strength parameters was analyzed based on the results of an example. Secondly, according to the linear softening attenuation law of soil material strength parameters, the functional relationship between internal friction angle and cohesion was deduced. The relationship was introduced into the classical strength reduction method, and a double reduction coefficient method based on the law of soil softening was proposed. Finally, the numerical result shows that the attenuation law of strength parameters of geotechnical materials is fully taken into account in the calculation, and the calculation process is more in line with the actual situation.

double strength reduction method; the critical strength parameter curve; reduction ratio; parameter softening law

P642.22

A

1672 − 7029(2019)09− 2215 − 08

10.19713/j.cnki.43−1423/u.2019.09.012

2018−11−28

国家自然科学基金资助项目(51578232)

苏永华(1965−)，男，湖南涟源人，教授，博士，从事隧道和滑坡方向的研究；E−mail：yong_su1965@126.com

(编辑 涂鹏)