全埋式抗滑桩合理桩间距确定方法探讨

贺建清，吴昊天，龙锦坤，王康康，高文华

全埋式抗滑桩合理桩间距确定方法探讨

贺建清，吴昊天，龙锦坤，王康康，高文华

(湖南科技大学 岩土工程稳定控制与健康监测省重点实验室，湖南 湘潭 411201)

基于已有的桩间土拱简化计算模型，利用传递系数法确定作用于单位厚度土拱上的线分布压力。考虑跨中截面前缘土体实际处于三向受压状态，由此建立土体抗剪强度条件，并在此基础上，提出以桩间静力平衡条件、跨中截面前缘土体抗剪强度条件以及拱脚处截面强度条件确定桩间距，推导出符合工程实际的桩间距计算公式。通过具体的工程实例，阐述抗滑桩桩间距的计算过程，得到比较合理的计算结果；进行距宽比/影响参数的敏感性分析，研究结果表明：在其他因素不变的情况下，边坡稳定系数sd的选取，对距宽比/的取值有显著影响。桩周土体的黏聚力对距宽比/的取值有较大影响，内摩擦角对距宽比/值有影响，但影响程度较弱。

抗滑桩；土拱效应；桩间距；滑坡

抗滑桩是一种常用的边坡支挡结构。按照埋置情况可以分为全埋式桩、悬臂桩和埋入式桩，其中使用最多的全埋式桩和悬臂桩。桩间距是抗滑桩设计的一个重要指标，桩间距过大可能导致抗滑作用失效，桩间距过小会造成工程投资增加和施工困难，所以如何选择合理桩间距在抗滑桩设计中极为重要。关于桩间距的选择，王成华等[1]基于抗滑桩两侧摩阻力之和大于桩间滑坡推力这一控制条件，不考虑土拱的强度条件，提出了桩间距的估算公式。蒋良潍等[2]以拱脚为最不利位置，利用土体的受压极限破裂方位及强度条件，推导了拱轴线与桩间距的简便计算式。李邵军等[3]基于土力学和弹性力学基本理论，结合土拱内部土体极限平衡条件建立了最大桩间距控制方程。周德培等[4−7]从桩间土拱效应形成机理出发，分析抛物线形土拱实际受力状态，认为拱顶截面前缘土体处于单向受力状态，根据抗滑桩桩侧的静力平衡条件、拱脚截面处的莫尔—库伦强度条件以及拱顶截面前缘土体的极限平衡条件，确定了悬臂桩的合理桩间距。刘涛等[8]根据最危险滑体中土拱的平衡条件、统一强度理论的强度条件和桩后土体发挥作用条件，提出2种适用于三维多层滑坡体模型的最小桩间距计算方法。从已有研究来看，针对悬臂桩合理桩间距的研究远多于全埋式抗滑桩，与全埋式抗滑桩在工程实际中的广泛应用不相适应。基于此，本文在已有研究成果的基础上，通过对边坡工程中抗滑桩间形成的土拱进行受力分析，认为土拱跨中截面前缘土体实际处于三向受压状态，并由此建立跨中截面强度条件，提出以桩间土静力平衡条件、土拱跨中截面及拱脚处截面强度条件来建立全埋式抗滑桩合理桩间距的计算方法，以符合工程实际。

1 桩间土拱简化计算模型

抗滑桩桩间土拱的形成是桩间土体在滑坡推力作用下产生不均匀变形，调动土体自身抗剪强度抵抗外力的结果，所产生的拱形必然使土体介质能最大限度地发挥其强度作用，结构力学上称这种拱形为“合理拱轴线”。合理拱轴线的每一截面上只存在压力，没有弯矩和拉力，适合于土体抗压不抗拉的特点[9−11]。在滑坡推力均匀分布于桩间岩土体的假设下，合理拱轴线应为二次抛物线[12]。图1为桩间土拱简化计算模型。拱跨距为，矢高为，作用于单位厚度土拱上的线分布压力为。

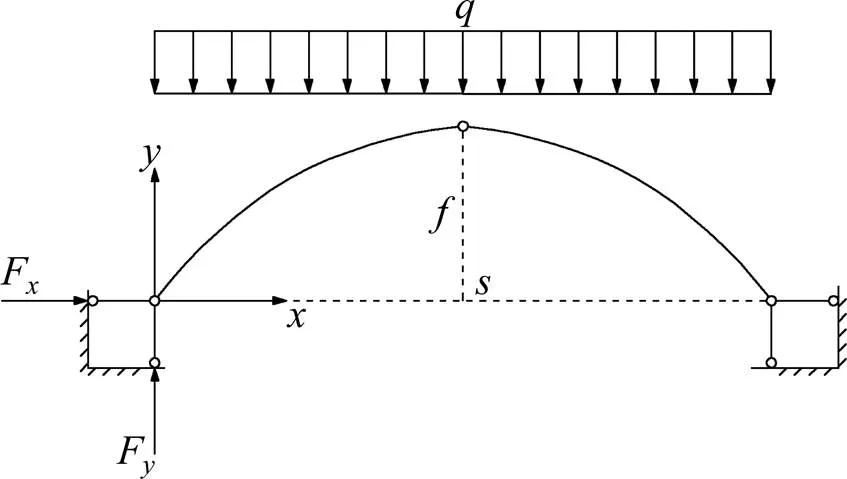
图1 桩间土拱简化计算模型

由结构力学三铰拱原理分析可得拱轴线方程

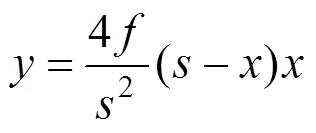
令=/，则式(2)变为

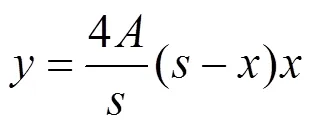
拱脚支座反力

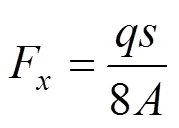
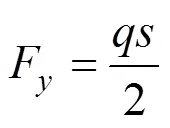
2 滑坡推力确定

2.1 剩余推力计算

关于剩余推力的计算有各种假定和算法，本文拟采用目前最常用的传递系数法[13−14]。

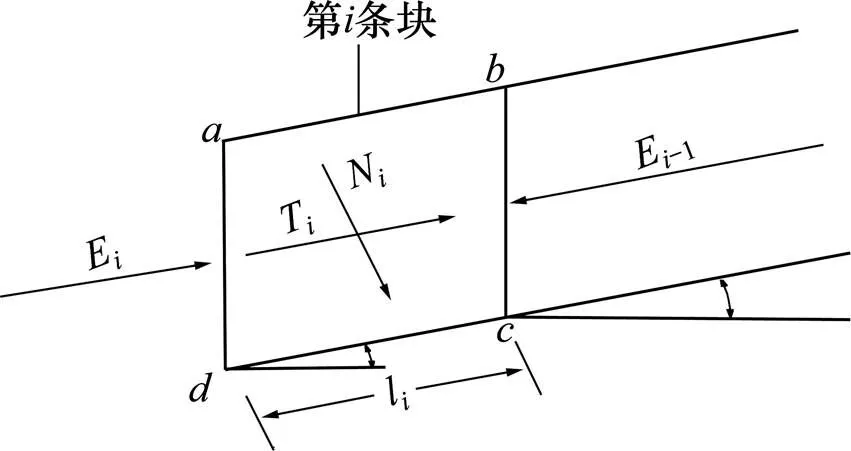
图2 剩余推力计算简图

图2中为滑坡体中的第条块，在其上界面上，作用有由第−1条块传下来的剩余推力E−1，其方向平行于上一条块的滑动面(倾角为−1)。第条块的自重可以分解为N和T2个分力，分别垂直和平行于该条块的滑动面，第条块传至第+1条块的剩余推力为E，E平行于滑动面，其值为

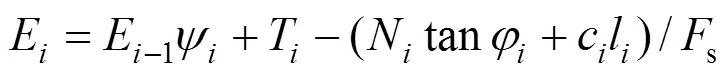
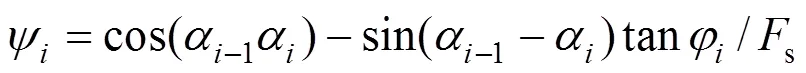
式中：s为边坡稳定系数；Ψ为传递系数；c和φ为第条块滑动面的的黏聚力和内摩擦角；l为第条块滑动面的长度；α1和α分别为第−1条块、第条块的滑动面坡角。

将式(5)转换可得E−1，其值为

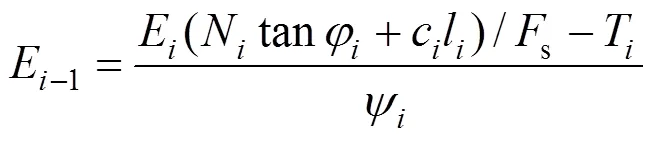
2.2 作用在土拱上的滑坡推力

图3(a)为一抗滑桩治理边坡，未设桩前边坡体处于临界稳定状态。任意设定一边坡稳定系数s，由顶端条块1，0=0，可由式(5)求得1，进而自上而下依次类推求得各条块的剩余推力。经反复设定边坡稳定系数进行试算，当坡脚处剩余推力E逼近0时，可认为该边坡稳定系数为加固前的边坡稳定系数，设该边坡稳定系数为s0，并可得图3(b)中所示天然剩余推力曲线。

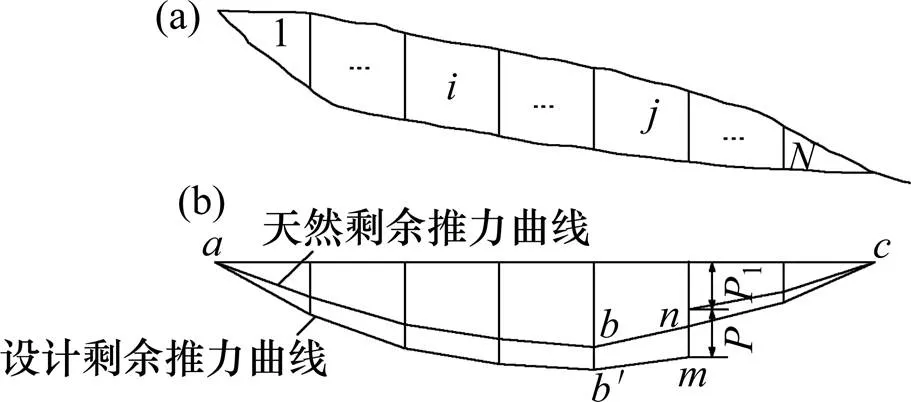
(a) 天然状况；(b) 设计状况

如图3(a)，选取一个合适的抗滑桩位置(第条块下界面)，并根据规范要求选择合适的边坡稳定系数sd。同上，可由式(5)自上而下依次求得抗滑桩以上边坡各条块的设计剩余推力。由底端条块，E=0，可由式(7)求得E−1，自下而上依次求得抗滑桩以下边坡各条块的设计剩余推力。从而得到一条不连续的设计剩余推力曲线′，见图3(b)。忽略土拱矢高和厚度，视土拱与桩位于同一位置[13]，土拱后条块传至土拱部顶剩余推力为+1，1为土拱在承受荷载时对土拱以下边坡土体或围岩产生的反力，即为边坡达到设计安全系数时，土拱应承受的载荷，即为作用在土拱上的滑坡推力。

2.3 单位厚度土拱上的线分布压力

剩余推力在条块界面上的分布与滑坡的类型、部位、滑坡体岩土性质、变形等有关。根据土压力的特点，假定作用在土拱顶部和底部的侧水平压力沿深度呈三角形分布[15]。

作用单位厚度土拱顶部的线分布压力为

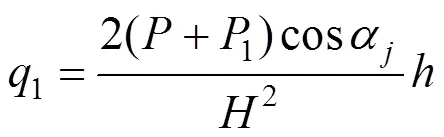
式中：为抗滑桩处地表以下埋深；为抗滑桩处滑坡体厚度；α为第条块的滑动面坡角。

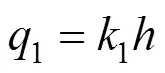
土拱在承受荷载时，作用在单位厚度土拱底部线分布反力为

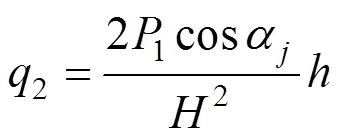
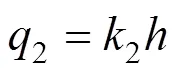
由式(9)和式(11)得单位厚度土拱上的线分布压力，其值为

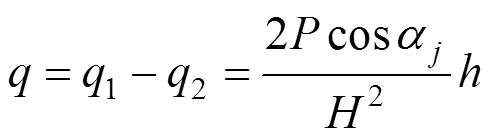
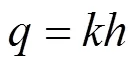
3 合理桩间距的确定

基于前人的研究成果[6−7]分析可知，桩间土拱可能发生破坏的情形如下：1)桩身强度不够发生断裂；2) 桩身刚度不够或嵌固不牢发生偏移；3)桩两侧摩阻力之和小于作用在土拱上的滑坡推力； 4)土拱内部发生剪切破坏。

由于抗滑桩的截面积一般较大、桩身混凝土强度较高，其强度和刚度足以承担土拱传递的滑坡推力，且有足够的锚入深度，并锚固于坚硬的岩土体中，桩身断裂或偏移的情况可以忽略。因此，土拱破坏主要是由桩土界面和土拱内部剪切破坏引起的。本文从极限破坏条件入手，结合桩间土拱的几何特征，确定全埋式抗滑桩的合理桩间距。

3.1 基本假定

考虑土体抗压不抗拉的特点及桩土相互作用的复杂性，同时为了简化计算，建立如下假定：

1) 拱后坡体滑坡推力沿拱跨方向均匀分布，因拱前非临空面，土拱跨中截面前缘土体实际处于三向受压状态；

2) 视桩间土拱受力状态为平面应变问题；

3) 抗滑桩的强度和刚度极大，具有足够的锚入深度，并锚固于坚硬的岩土体中，可视其水平位移为0；

4) Mohr-Coulomb强度准则适用于桩土接触面及土拱内部。

3.2 桩土接触面的剪切破坏

要保证抗滑桩桩间土拱正常发挥作用，桩间土体沿滑移方向需要满足静力平衡条件，即桩侧面的摩阻力不小于作用在土拱上的滑坡推力。

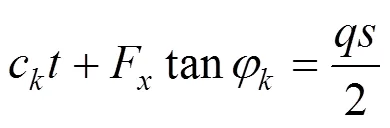
式中：为拱圈厚度；c和φ为桩接触面的黏聚力和内摩擦角，为计算简便，c和φ为土体的和。则式(14)变为

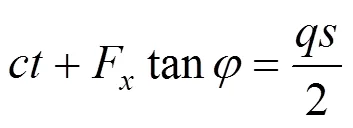
将式(3)代入式(15)得

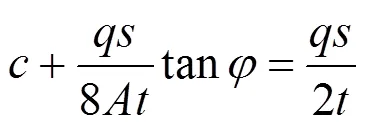
令=/，则式(16)则变为

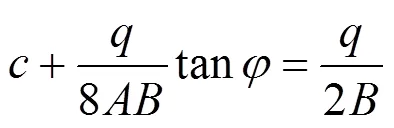
3.3 桩间土拱剪切破坏

土拱跨中截面为最不利截面，跨中截面前缘点(如图4所示)为最不利受力点，要保证土拱稳定并充分发挥传力作用，前缘点处土体必须满足强度条件。前缘点处土体的应力状态如图4所示。

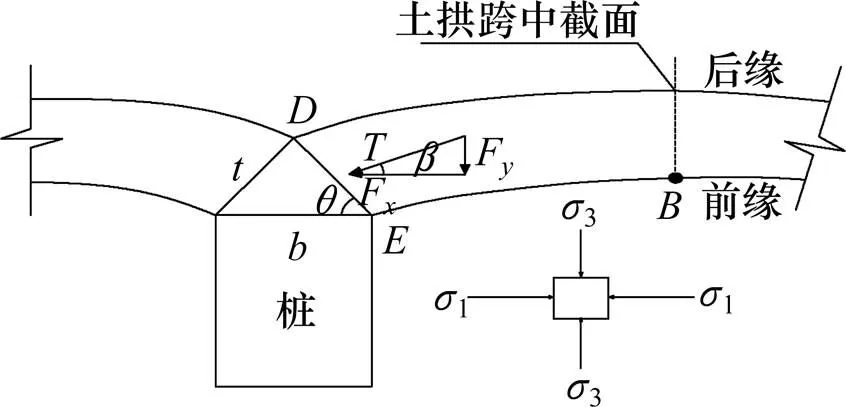
图4 相邻土拱交汇处的三角形受压区

由于跨中截面弯矩为0，前缘点处的应力为

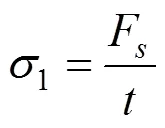
由极限平衡条件得

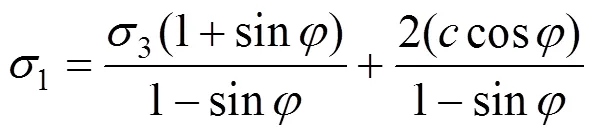
将式(18)代入式(19)得

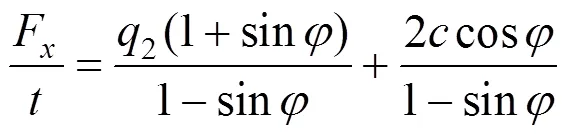
将式(3)代入式(20)得

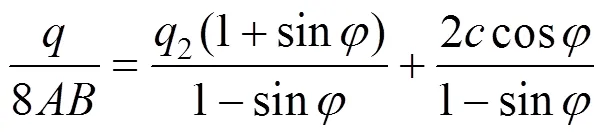
将式(21)代入式(17)得

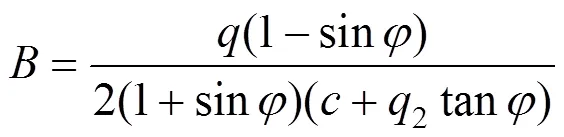
将式(22)代入式(21)得

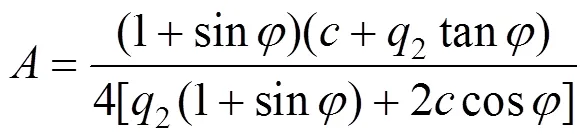
3.4 相邻土拱交汇受压区剪切破坏

相邻土拱在桩顶形成如图4所示的三角形受压区。要使三角形受压区能正常发挥作用而不被破坏，确保土拱稳定，截面应该满足强度条件

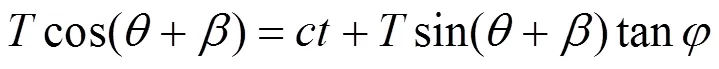
式中：为作用于截面上的合力；为截面与水平方向的夹角；为合力与水平方向的夹角。

由式(3)，式(4)，式(24)和式(25)整理得

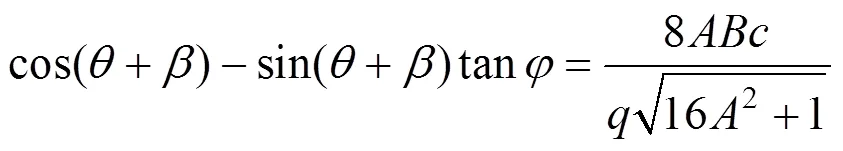
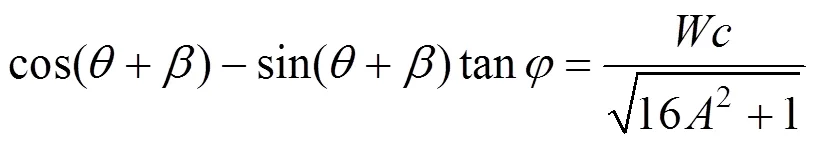
由式(3)，式(4)和图4可得

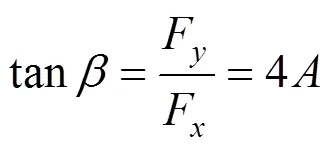
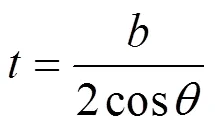
式中：为桩宽。

由式(28)求出，再由式(27)算得，进而由式(29)求出拱圈厚度，最后由=/、式(22)确定拱跨，其表达式为：

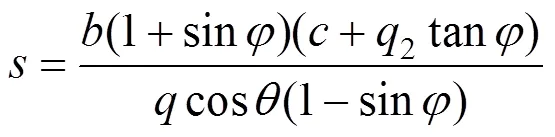
将式(11)和式(13)代入式(27)得

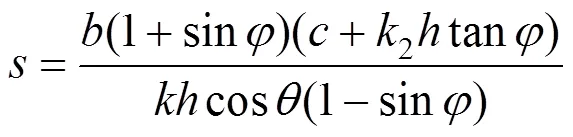
由式(31)可得相邻两桩的中心距

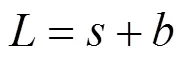
由式(31)、式(32)可得相邻两桩的中心距与桩宽之比(以下简称距宽比)

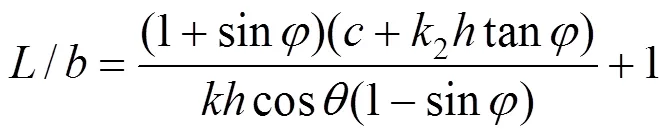
4 工程算例

4.1 桩间距确定

滑坡位于某小区后山，系由强降雨诱发的小型牵引式土质滑坡。滑坡区出露的地层主要为古生界泥盆系地层以及第4系松散堆积层。滑坡剖面工况见表1。

采用传递系数法分析滑坡的稳定性，其剩余推力曲线见图5(b)中的实线，加固前边坡稳定系数s0为0.97，按《建筑边坡工程技术规范》边坡稳定性评价标准，滑坡处于不稳定状态。经技术经济比较，采用抗滑桩加固处理。按照规范要求，边坡设计稳定系数sd取1.25，桩设置于第7条块和第8条块界面处，桩周土体强度指标采用滑面强度指标，设计剩余推力曲线见图5(b)中的虚线。桩截面尺寸为2.0 m×3.0 m，桩受荷段长度为5.0 m，锚入深度为7.0 m。将滑坡工况参数代入本文法，得到不同埋深处相应的桩间距取值，见图6。由图6可知，抗滑桩埋深越深，桩间距取值单调减小，于滑面处达最小值。为安全起见，取桩间距最小值为合理桩间距，即=2.39，实际工程取值为2，本文法计算结果接近实际工程取值。

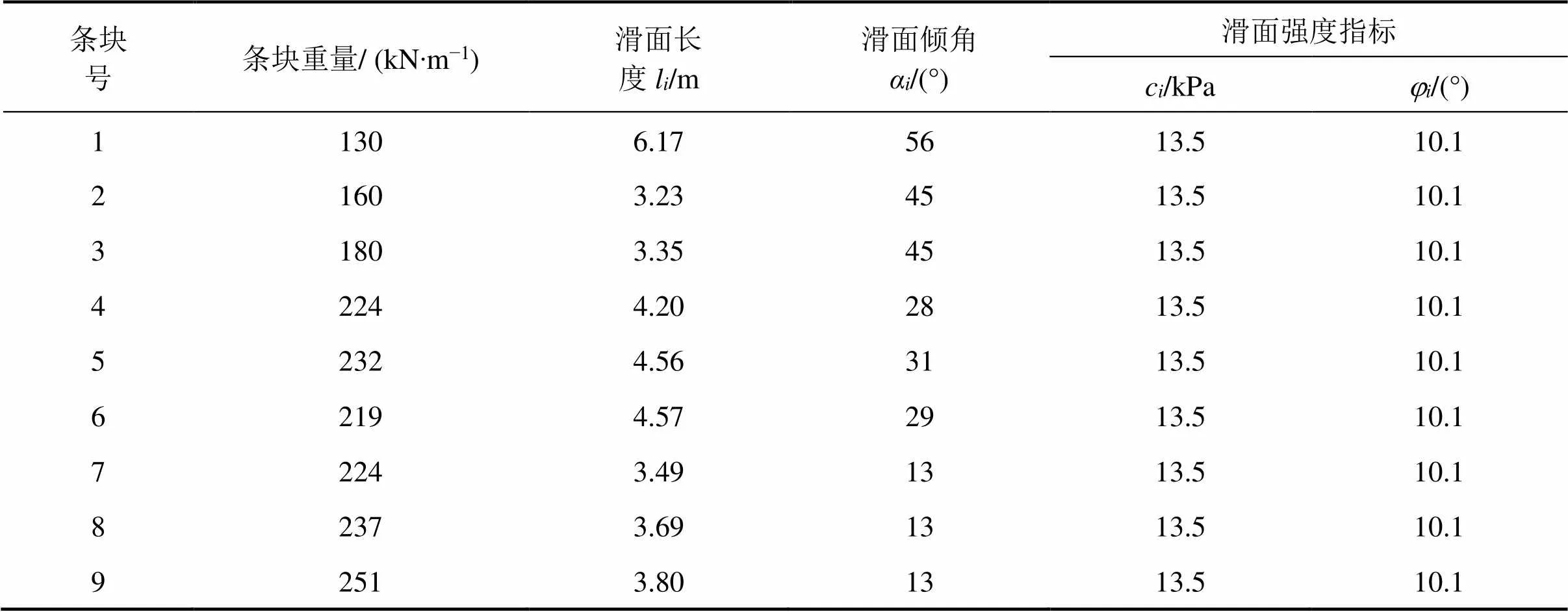
表1 滑坡剖面工况

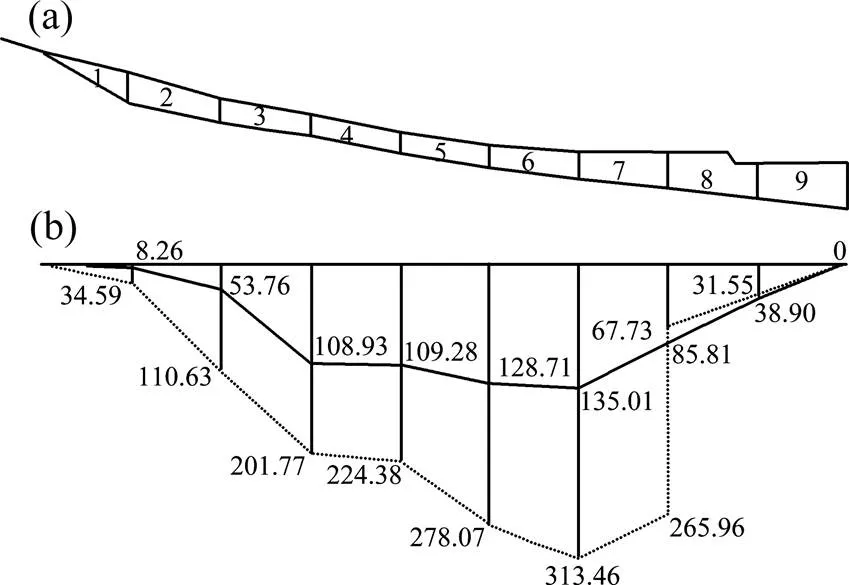
(a) 天然状况；(b) 设计状况

4.2 距宽比影响参数的敏感性分析

由前述推导过程可知，距宽比/受诸多参数的影响，与相关参数的关系式可表示为

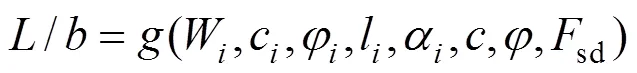
对于某一具体工程而言，Wi，li和αi可视为常量。滑面及桩周土体强度指标ci，φi，c和φ受气候、地下水的影响不断变化；Fsd值取决于边坡类型与工程安全等级，其取值反映了滑面剪切强度的变化。有鉴于此，本文基于工程算例讨论距宽比L/b与c，φ和Fsd的关系。

4.2.1 黏聚力对距宽比/影响的敏感性分析

距宽比/与的关系见图7。从图7可以看出，在边坡稳定系数sd相同的条件下，距宽比/与的关系曲线为一条下凹的曲线。曲线的起始段，距宽比/随着黏聚力的增加而减小，当黏聚力=5 kPa左右时，曲线接近谷底，而后距宽比/随着黏聚力的增加而单调增加。不同sd值下的/~关系曲线接近平行。随着sd值增大，黏聚力对距宽比/值的影响程度增大，即距宽比/对值较敏感。

4.2.2 内摩擦角对距宽比/影响的敏感性分析

距宽比/与的关系见图8。由图8可以看出，在边坡稳定系数sd相同的条件下，距宽比/与的关系曲线亦为一条下凹的曲线。曲线的起始段，距宽比/随着内摩擦角的增加而减小，当黏聚力=10°左右时，曲线接近谷底，而后距宽比/随着内摩擦角的增加而单调增加。不同sd值下的/~关系曲线接近平行。随着sd值增大，内摩擦角对/值有影响，但影响程度较弱，即距宽比/对值不是很敏感。

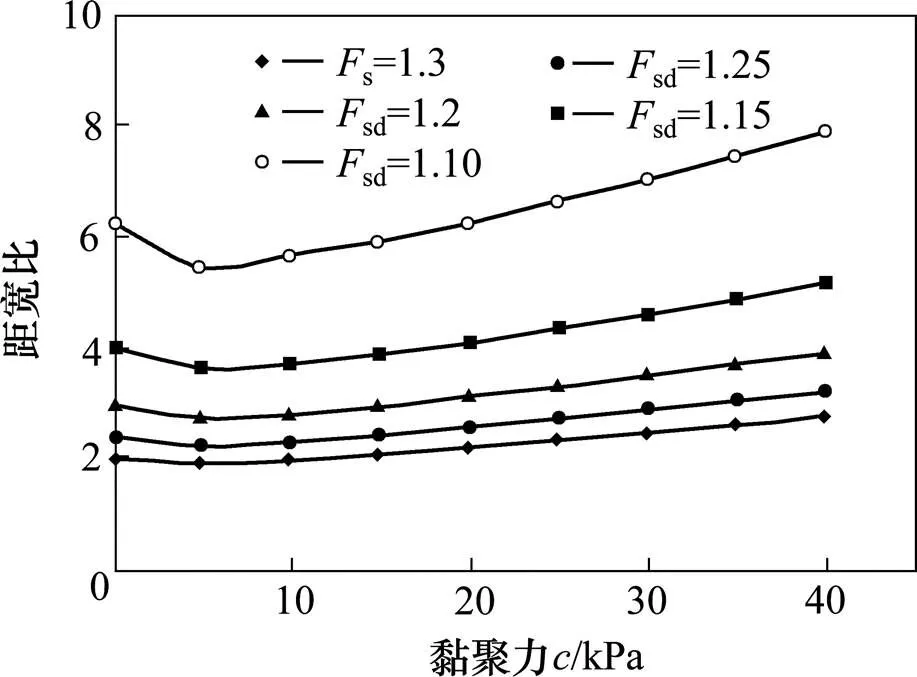
图7 L/b与黏聚力c的关系曲线(φ=10.1°)

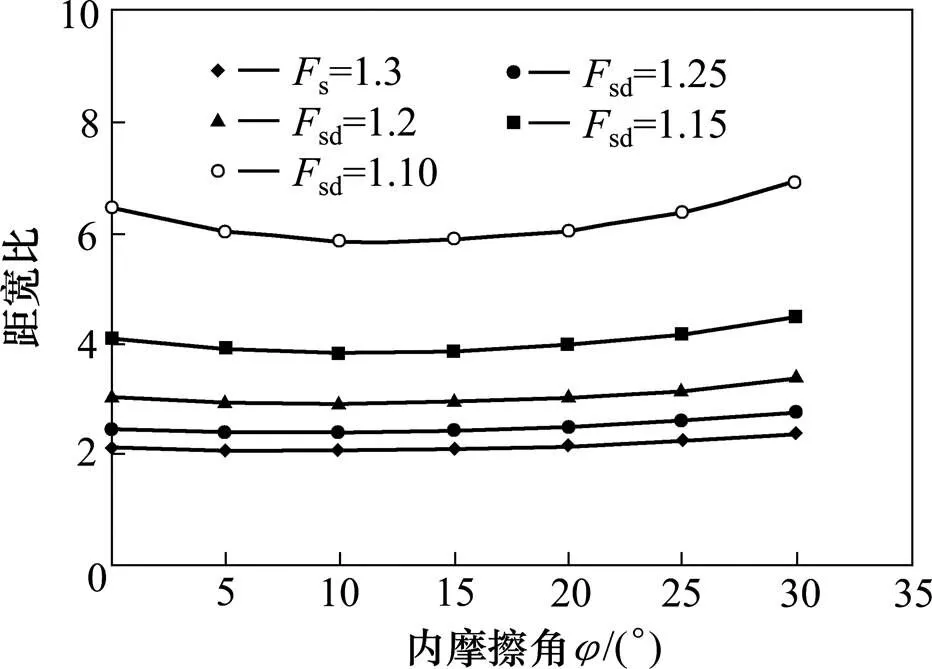
图8 L/b与内摩擦角φ的关系曲线(c=13.5 kPa)

4.2.3sd取值对/影响的敏感性分析

利用工程算例，选取不同的sd值，距宽比/与sd的关系见图9。

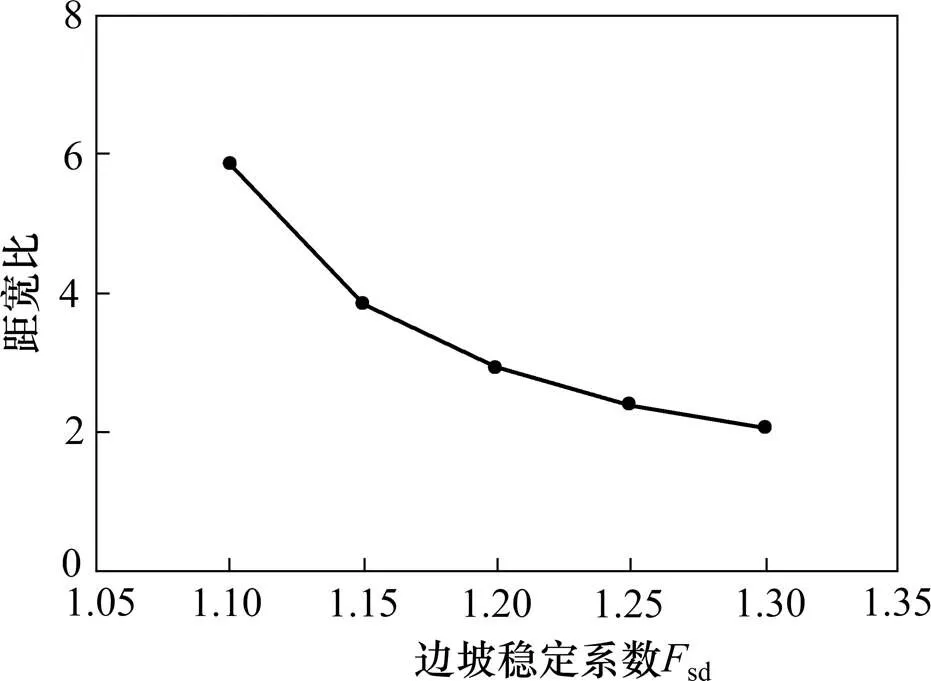
图9 L/b与边坡稳定系数Fsd的关系曲线

由图9可以看出，距宽比/随着sd值增加单调减小，且减小幅度很大。说明sd值的选取，对/的取值有显著影响，/对sd值极其敏感。所以在确定桩间距时，对sd值的选取一定要慎重。

5 结论

1) 认为土拱跨中截面前缘土体实际处于三向受压状态，由此建立跨中截面强度条件，提出以桩间静力平衡条件、跨中截面以及拱脚处截面强度条件确定桩间距，推导出了符合工程实际的桩间距计算公式，并通过工程实例验证了公式的合理性。

2) 进行距宽比/影响参数的敏感性分析，分析结果表明：边坡稳定系数sd值的选取，对距宽比/的取值有显著影响，在确定桩间距时，对sd值的选取一定要慎重。桩周土体的黏聚力对/的取值有较大影响，桩周土体的内摩擦角对距宽比/有影响，但影响程度较弱。

[1] 王成华, 陈永波, 林立相. 抗滑桩间土拱力学特性与最大桩间距分析[J]. 山地学报, 2001, 19(6): 556–559. WANG Chenghua, CHEN Yongbo, LIN Lixiang. Soil arch mechanical character and suitable space between one another anti-sliding pile[J]. Journal of Mountain Science, 2001, 19(6): 556–559.

[2] 蒋良潍, 黄润秋, 蒋忠信. 黏性土桩间土拱效应计算与桩间距分析[J]. 岩土力学, 2006, 27(3): 445–450. JIANG Liangwei, HUANG Runqiu, JIANG Zhongxin. Analysis of soil arching effect between adjacent piles and their spacing in cohesive soils[J]. Rock and Soil Mechanics, 2006, 27(3): 445–450.

[3] 李邵军, 陈静, 练操. 边坡桩−土相互作用的土拱力学模型与桩间距问题[J]. 岩土力学, 2010, 31(5): 1352− 1358. LI Shaojun, CHEN Jing, LIAN Cao. Mechanical model of soil arch for interaction of piles and slope and problem of pile spacing[J]. Rock and Soil Mechanics, 2010, 31(5): 1352−1358.

[4] 周德培, 肖世国, 夏雄. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报, 2004, 26(1): 132−135. ZHOU Depei, XIAO Shiguo, XIA Xiong. Discussion on rational spacing between adjacent anti-slide piles in some cutting slope projects[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 132−135.

[5] 章玲玲, 林海. 基于土拱效应的板桩码头遮帘桩间距的设计计算[J]. 岩土工程学报, 2013, 35(增2): 1134− 1137. ZHANG Lingling, LIN Hai. Design calculation on spacing of barrier piles for sheet-pile wharf based on soil-arching effect[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Suppl 2): 1134−1137.

[6] 杨雪强, 吉小明, 张新涛. 抗滑桩桩间土拱效应及其土拱模式分析[J]. 中国公路学报, 2014, 27(1): 30–37. YANG Xueqiang, JI Xiaoming, ZHANG Xintao. Analysis of soil arching effect between anti-slide piles and different arch body modes[J]. China Journal of Highway and Transport, 2014, 27(1): 30−37.

[7] 赵明华, 陈耀浩, 杨超炜. 考虑土拱作用抗滑桩合理桩间距确定方法研究[J]. 岩土工程学报, 2015, 37(增2): 16−21. ZHAO Minghua, CHEN Yaohao, YANG Chaowei. Methods for determining rational spacing between anti-slide piles considering soil arching effects[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(Suppl 2): 16−21.

[8] 刘涛, 张海宽, 张友, 等. 三维复合多层滑坡体中抗滑桩最小桩间距研究[J]. 岩石力学与工程学报, 2018, 37(2): 473–484.LIU Tao, ZHANG Haikuan, ZHANG You, et al. Minimum pile spacing between stabilizing piles in 3D composite multilayer landslide[J]. Chinese Journal of Geotechnical Engineering,2018,37(2): 473–484.

[9] Terzaghi K. Theoretical soil mechanics[M]. London: Chapman and Hall, Limited, 1951.

[10] Handy R L. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302−318.

[11] Bosscher P J, Gray D H. Soil arching in sandy slopes[J]. Journal of Geotechnical Engineering, 1986, 112(6): 626− 645.

[12] Iglesia G R, Einstein H H, Whitman R V. Investigation of soil arching with centrifuge tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 140(2): 1−13.

[13] GB 50330—2013, 建筑边坡工程技术规范[S]. GB 50330—2013, Technical code for building slope engineering[S].

[14] LIU W, LI Q, LU J, et al. Improved plane layout of stabilizing piles based on the piecewise function expression of the irregular driving force[J]. Journal of Mountain Science, 2018, 15(4): 871−881.

[15] X Shiguo. Approximate theoretical solution of distribution modes of landslide thrust on anti-sliding piles in soil-like slopes or landslides[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1): 120−123.

Method for determining rational spacing between adjacent embedded anti-slide piles

HE Jianqing, HU Haotian, LONG Jinkun, WANG Kangkang, GAO Wenhua

(Hunan Provincial Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring, Hunan University of Science and Technology, Xiangtan 411201, China)

Using the transfer coefficient method, the linearly distributed pressureacting on the soil arch per unit thickness were determined based on the existing simplified calculation model of soil arch between piles. Considering the fact that the front soil of the mid-span section is in triaxial compression, the strength criterion of the soil was established. On this basis, a calculation formula for rational spacing between adjacent anti-slide piles that conforms to the actual engineering situation was derived according to the static equilibrium condition between piles, the shear strength condition of the soil at the front edge of the cross section and the section strength condition at the arch foot. Then, a calculation process to determine rational spacing between adjacent anti-slide piles was demonstrated with the engineering practice, and the reasonable calculation results were obtained. The sensitivity of/to those influencingparameters was analyzed and it was found that without consideration of other factors, the selection of the stability coefficientsdhas a significant effect on the value ofThe cohesionof the soil around the pile has a great influence on the value of/, and the internal friction anglealsohas an effect, but rather small, on the/value.

anti-slide pile; soil-arch effect; spacing between adjacent piles; landslide

TU473.1；P642.22

A

1672 − 7029(2019)09− 2192 − 07

10.19713/j.cnki.43−1423/u.2019.09.009

2018−12−04

国家自然科学基金资助项目(41272324)；湖南省自然科学基金资助项目(2017JJ4039)

贺建清(1964–)，男，湖南湘乡人，教授，博士，从事边坡工程及轻型支挡结构方面的教学与研究工作；E−mail：hjqing2000@163.com

(编辑 蒋学东)