基于ROS的六关节机器人运动规划研究
2019-03-20郭建根阚宏林
郭建根,双 丰,阚宏林
(1.安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000;2.中国科学院合肥智能机械研究所,安徽 合肥 230031)
随着社会发展的需求,机器人的工作环境日趋复杂,对机器人的控制系统提出了更高的要求。而机器人厂商都是开发自身的软件接口,可移植性差,只能应用于本企业生产的机器人,大量复杂冗余的代码严重影响了开发者的工作效率。开源机器人操作系统(Robot Operating System,ROS)能够很好地解决这些问题。目前,国内外对基于ROS的机器人运动轨迹规划已经做了大量研究。如美国匹兹堡实验室和Inter公司联合开发的移动操作机器人(Home Exploring Robotic Butler,HERB),该移动机器人能够实时构建地图定位以及利用构建好的地图在室内自由移动,完成取物品和清理餐桌等任务[1]。钱伟[2]等基于ROS操作平台,利用RRT算法并对其改进,实现了冗余自由度机械臂在动态环境下的自主规划。刘磊[3]等研究了基于ROS平台下的机器人轨迹规划,分析其各关节角度变化和末端插补误差,使机械臂各关节运行轨迹平滑,末端位置精度满足要求。温宽昌[4]等利用三角函数与S形速度曲线混合插值,保证了机器人关节加速度连续变化,避免了柔性冲击。基于ROS机器人操作系统,以六关节机器人为研究对象,分析机器人在笛卡尔空间的直线、圆弧插值,利用ROS集成的RRT算法实现机器人无碰撞路径规划,进行避障运动测试。
1 ROS机器人操作系统
ROS是Willow Garage公司2010年发布的开源机器人操作系统,能够提供类似传统操作系统的诸多功能,采用分布式架构,通过各功能独立的节点(Node)传递消息实现任务的分层次运行,凭借着点对点的设计、多语言支持、免费且开源、代码易拓展性等优点,在机器人领域得到了广泛的应用和研究[5]。此外,ROS集成了很多仿真工具包(如Rviz,Gazebo,Moveit!等),功能十分强大,为人机交互和机器人运动规划提供了极大的便利。
2 仿真平台搭建
2.1 机器人运动学建模
在SolidWorks中建立六关节机器人模型,并建立关节坐标系如图1所示。机器人机械臂D-H参数如表1所示。
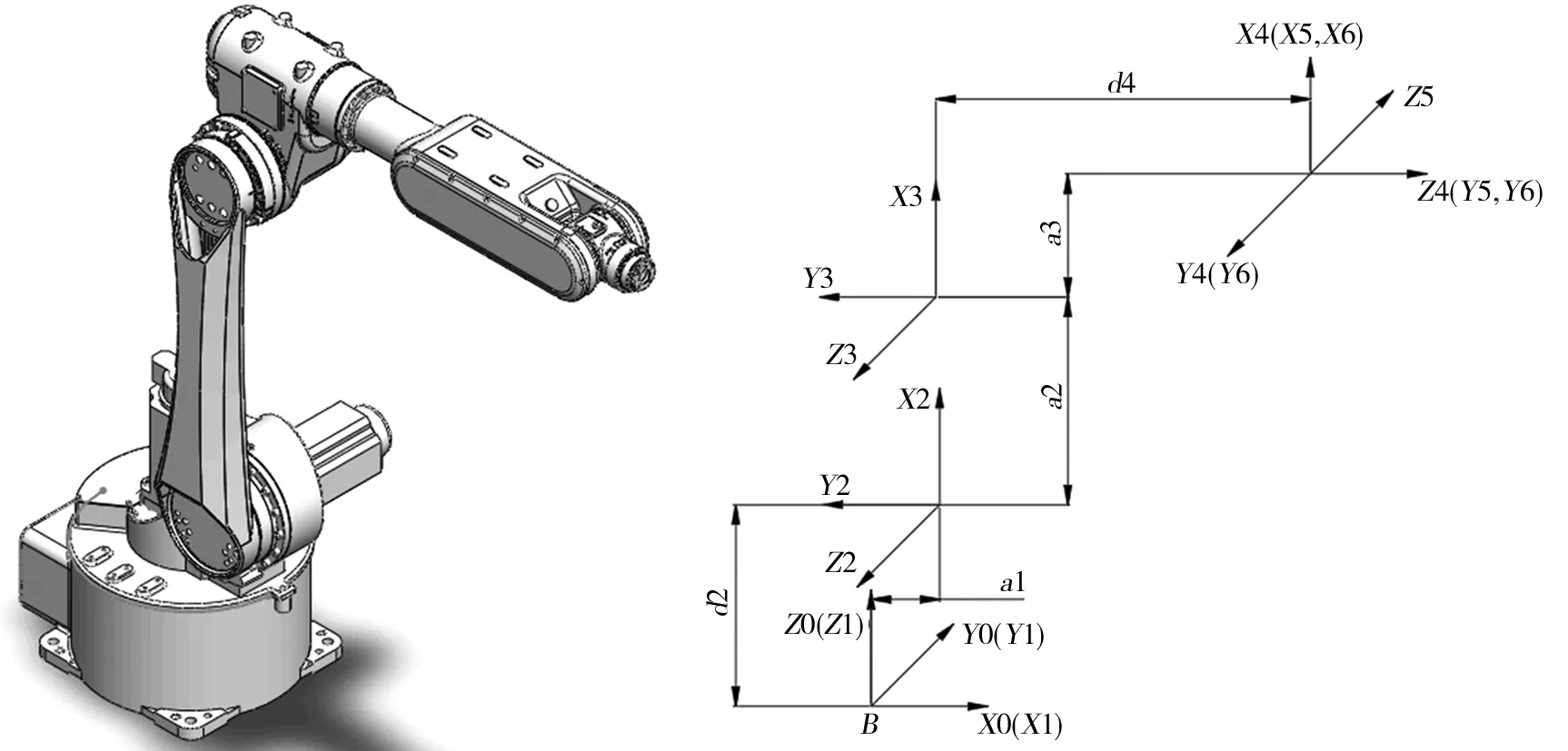
图1 机器人建模
利用旋转运动和平移运动描述相邻坐标系i-1和i之间的位姿关系,从而建立齐次变换矩阵[6],描述如式(1)所示:
i-1Ti=RX(αi-1)DX(αi-1)RZ(θi)DZ(di),
(1)
i-1Ti的通用表达式为:
(2)
式中,cθi=cosθi,sθi=sinθi,cαi=cosαi,sαi=sinαi,机器人的运动学方程为:
0T6=0T11T22T33T44T55T6,
(3)
联立式(2)、式(3)并代入表1的D-H参数,即可得机器人末端相对于基座的位姿。
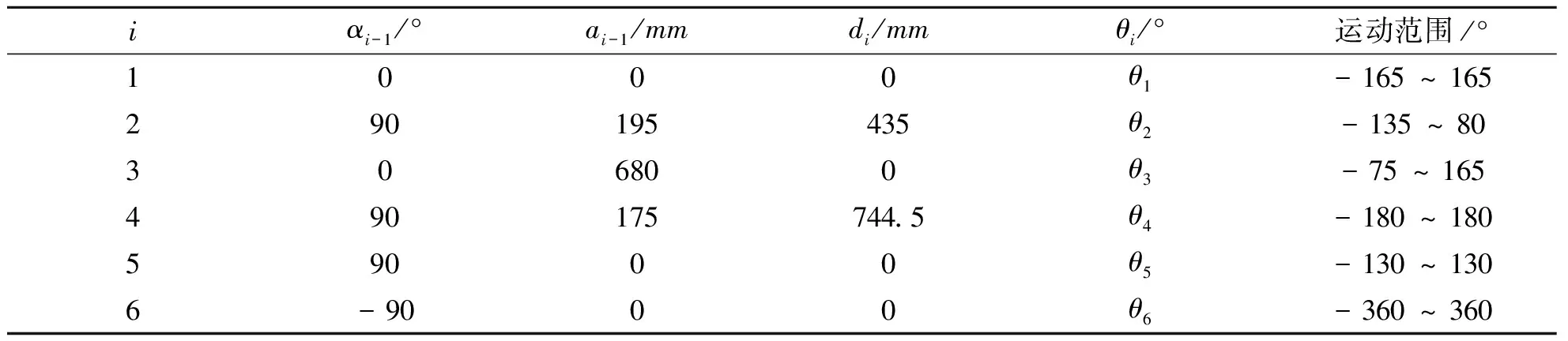
表1 机械臂D-H参数
2.2 获取URDF文件
在SolidWorks中建立机器人模型后,可以用ROS官方的Sw2urdf插件来生成URDF文件,需要在其中定义各个连杆的相对关系以及关节轴的位置、速度等一些物理参数的取值范围,然后直接生成URDF模型,整个过程如图2所示。
在ROS中使用可视Check_urdf工具可以生成机器人连杆的父子级关系,机器人连杆关系如图3所示。图3能清晰地显示机器人的结构。
2.3 Moveit!运动配置
ROS MoveIt!是专门为可移动操作平台开发的软件包,它集成了运动规划、三维感知、运动控制领域的最新成果,提供了一个开发高级机器人应用的软件平台。ROS Movelt!整体框架如图4所示。由图4可知,在MoveIt!架构中,Move_Group节点处于核心地位,此节点作为一个“管理器”,将各个接口组合到一起,Move_Group使用ROS topic和action的方式与机器人通信,获取机器人的实时状态和传感器数据等信息,通过FollowJointTrajectoryAction接口控制机器人运动。
MoveIt!设置助手MoveIt Setup Assistant会根据导入的URDF机器人模型生成Semantic Robot Description Format(SRDF)文件,运动学配置文件和运动规划库配置文件以及相应的启动文件,完成机器人的配置、可视化和仿真等工作,其配置流程如图5所示。
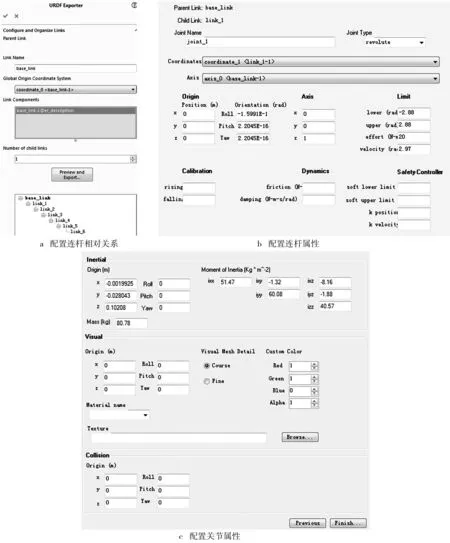
图2 URDF文件生成

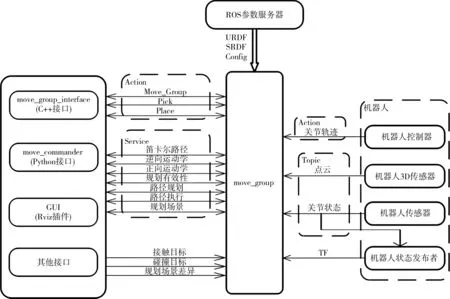
图4 ROS MoveIt!整体框架
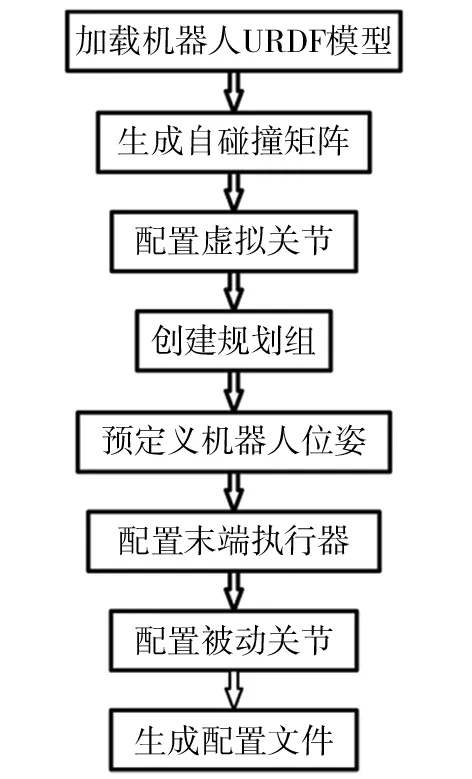
图5 MoveIt!配置流程
生成的配置文件中主要有config和launch文件,其中config文件下的
3 笛卡尔空间位置规划仿真
空间很多曲线都可以分割为多段直线或圆弧,这是机器人笛卡尔空间下轨迹规划最基本的组成部分。在MoveIt!中,选择Kinematics and Dynamics Library(KDL)求解器,通过数值迭代求解机器人逆运动学。
3.1 空间直线轨迹规划
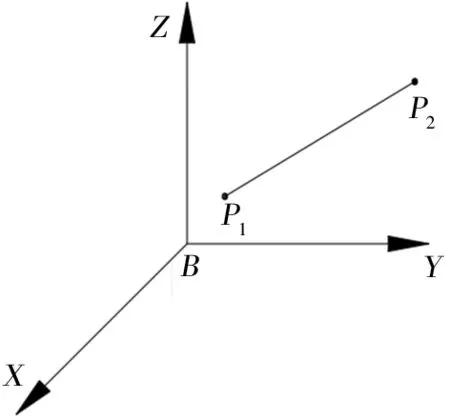
图6 笛卡尔空间直线轨迹
空间直线的轨迹规划是已知直线起始点的位置和姿态,按照插补算法求直线轨迹上中间点(插补点)的位置和姿态。
已知机器人末端执行器起始点P1(x1,y1,z1)和终止点P2(x2,y2,z2),并且以直线从P1点运动到P2点,笛卡尔空间直线轨迹如图6所示。
设定笛卡尔空间中直线插值运动笛卡尔空间直线轨迹最大速度和加速度分别为vmax和a,则可计算出匀速运动时间和加速时间tvm和ta,在任意时刻t∈[0,T],当前位置距离初始位置P1的位移为VSt,在笛卡尔空间中的基坐标系(参考坐标系)下,使用矢量对起始点P1和终止点P2进行描述[6]:
P1=x1i+y1j+z1k,
(4)
P2=x2i+y2j+z2k,
(5)
则矢量P21可表示为:
P21=P2-P1=(x2-x1)i+(y2-y1)j+(z2-z1)k,
(6)
空间直线的长度为:
(7)
设机器人末端执行器从起始点P1以速度v运动到终止点P2的总时间为T,则任意时刻t∈[0,T]机器人末端执行器的位置可表示为:
(8)
在ROS/RViz中的仿真结果如图7所示。

图7 直线插值运动仿真
3.2 空间圆弧轨迹规划
空间中不共线的3点可以确定唯一一个圆,设笛卡尔空间不共线的3点为P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3),机器人以圆弧从P1经过P2运动到P3。
(1)求圆心坐标N(x0,y0,z0)和圆弧半径R[7-9]。
过P1、P2、P3的平面方程为:
(9)
记为:
Ax+By+Cz+D=0,
(10)
其中
(11)
在笛卡尔空间圆弧的轨迹规划中,为了计算简便,需要先在圆弧所在平面新建一个坐标系N,原点为圆弧中心,在这新的直角坐标系中计算出圆弧的各插补点在新坐标系中的值,然后通过运动学关系将这些值映射到参考坐标系,记参考坐标系为B,从而得出各插补点在参考坐标系下的值。圆弧中心坐标可由3个平面(圆弧所在平面、P1P2中垂面、P2P3中垂面)的交点得出。
过P1P2中点且与P1P2垂直的平面方程为:
(12)
过P2P3中点且与P2P3垂直的平面方程为:
(13)
联立3个平面方程可得圆心坐标N(x0,y0,z0),从而圆弧半径:
(14)
(2)坐标变换,建立新坐标系N(N-UVW),如图8所示,以基坐标系表示坐标系N。
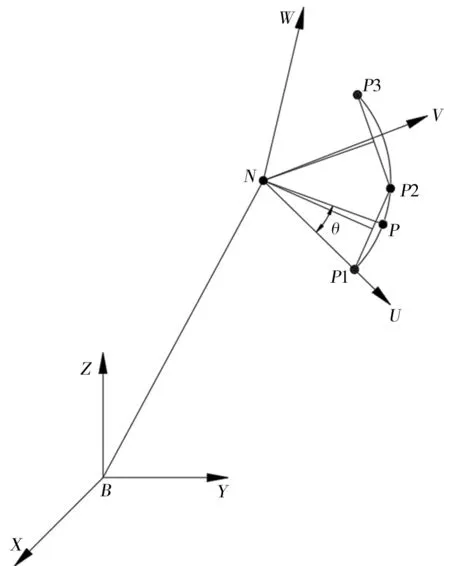
图8 笛卡尔空间圆弧轨迹
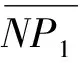
(15)
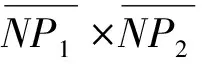
(16)
由右手定则可知V轴在U轴和W轴的叉乘方向,其单位向量为:
v=u×w,
(17)
由基坐标系到N-UVW的姿态变换矩阵为:
(18)
位置向量为:
BPN=(x0,y0,z0),
(19)
坐标系N相对于基坐标系B的位姿矩阵为:
(20)
笛卡尔空间圆弧的轨迹通过矩阵变换,可转化为新坐标系N中的一个二维平面圆,设圆弧上任意一点P(x,y,z),∠P1NP=θ,点P在坐标系N下的坐标向量为:
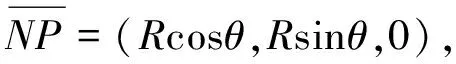
(21)
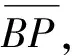
(22)
从而转化为在基坐标系下对圆弧进行描述,P的轨迹点组成了笛卡尔空间圆弧的轨迹,在ROS中的圆弧轨迹规划仿真结果如图9所示。

图9 圆弧插值运动仿真
4 避障规划
4.1 RRT算法原理
对于高维空间和复杂约束条件下的运动规划问题,一般采用快速搜索随机树(Rapidly-exploring Random Trees,RRT)算法,该算法基于随机采样进行规划,通过对采样点进行碰撞检测,把搜索方向导向无碰撞区域,从而规划出一条从初始点到目标点的无碰撞路径,尤其适合多自由度机器人在复杂环境和动态环境中的运动规划问题[10],其原理如图10所示。RRT算法的执行流程如图11所示。
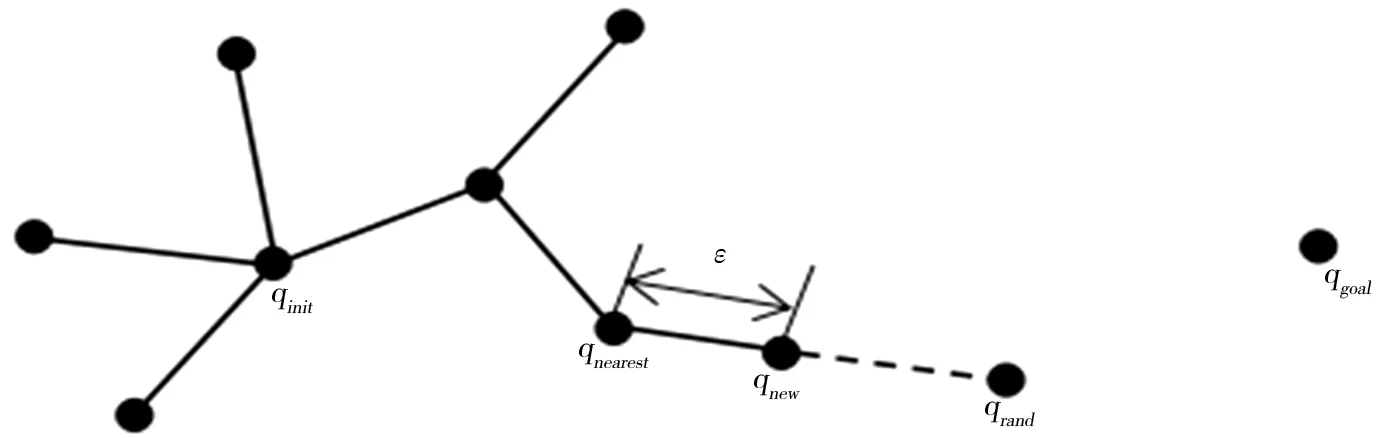
图10 RRT算法原理
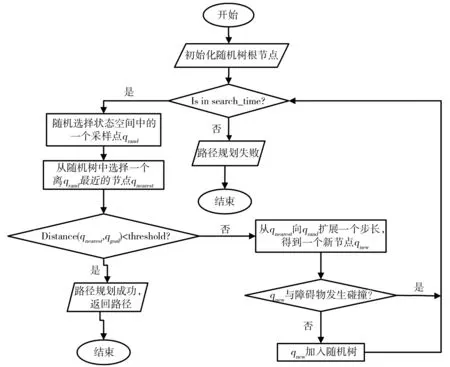
图11 RRT算法执行流程
(1)将初始点作为根节点,初始化根节点qinit;
(2)在状态空间随机采样一个点qrand;
(3)判断是否搜索超时;
(4)在已生成的随机树中选择一个距离qrand最近的节点qnearest;
(5)qnearest以步长ε向qrand扩展一段距离,得到新节点qnew;
(6)检测qnew是否与障碍物发生碰撞,若不发生碰撞,则进行随机树的生长,否则,放弃本次生长;
(7)重复步骤(2),直到qnearest与qgoal的距离小于设定的阈值;
(8)返回规划结果。
伪代码如下:
Function Build_RRT:BOOL(env:environment,T:RRT_Tree,qgoal:node)
varqrand,qnearest,qnew:node
while (search_time) do
qrand=Choose_Rand()
qnearest=Nearest(qrand,T)
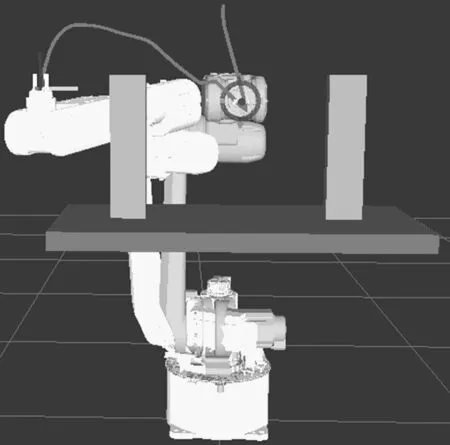
if (Distance(qnearest,qgoal) return T qnew=Extend(qnearest,qrand,ε) if (qnew≠NULL) then T.Add_Node(qnew) return false 在ROS Rviz中,添加MotionPlanning插件,选择OMPL运动规划库中的RRT算法,利用Python定义障碍物的尺寸并设置障碍物相对于机器人参考坐标系的位置,桌面高0.9 m,厚度0.05 m,两长方体大小一致,长宽高分别是0.1 m、0.05 m、0.4 m,如下所示: #设置桌面的高度 table_ground=0.9 #设置table、box1和box2的三维尺寸 table_size=[1,0.5,0.05] box1_size=[0.1,0.05,0.4] box2_size=[0.1,0.05,0.4] 设定机器人运动的起始点A(0,1.05,1.28)和目标点的位置B(0.5,1,1.25),机器人从两障碍物正中间开始运动,绕过左边障碍物运动至目标点,运行Python脚本执行RRT算法无碰撞路径规划,仿真结果如图12所示。 图12 RRT无碰撞路径规划 基于ROS平台,在SolidWorks中建立机器人模型,通过Sw2urdf插件将机器人3D模型转化为ROS下的urdf模型,通过MoveIt!和Rviz仿真工具实现了笛卡尔空间下的直线和圆弧轨迹规划。同时,基于RRT算法进行无碰撞路径规划,仿真结果表明,机器人能成功绕开障碍物运动到目标点,验证了算法的有效性。未来的研究工作将集中在机器人复杂环境下的无碰撞路径优化问题,减小关节电机运行时间并降低能量消耗。4.2 算法测试
5 结论
