利用跟随周期均值显著化序列异常数据的学习算法
2019-03-20冯富霞李森贵
冯富霞,李森贵
(1.安徽工程大学 计算机与信息学院,安徽 芜湖 241000;2.芜湖莫森泰克汽车科技有限公司,安徽 芜湖 241000)
序列数据在工业、医学、IT等行业十分常见,精确地找出序列中的异常数据是非常有价值的。异常检验方法有数学分布、DTW、概率后缀树、预测对比[1-2]、强力搜索[3]等,主要依据基础概率统计、邻近度、判断模型、回归模型[2,4]、神经网络、支持向量机等[5]。每种方法都有适用的要求,统计方法必须基于一定的数学分布;邻近度的距离或角度度量法对数据在序列中的次序和正负变化趋势不敏感,同时如果异常点和正常点的距离很小容易误判;判断模型需要大量内存和运算量;回归模型参数复杂,异常点和正常点的预测差值阈值敏感;神经网络、支持向量机算法复杂度高,需要大量内存和运算量。
计算机的硬件配置飞速提高,如果执行异常检测的硬件是计算机,甚至是云平台,不管计算量、数据量如何,任何算法都可以尝试。但是在有些场景下受硬件的约束极强,无法使用复杂度高的算法,同时又需要实时有效地检测出异常,终止异常并采取措施。例如工业控制系统序列数据异常检测[5-6]、产品附属的局部控制功能等。汽车车窗防夹为第二种实例,硬件配置极大受限,因此对防夹算法的运算量、存储量要求非常敏感,促使研发人员不断寻找简单有效的方法。防夹常用算法是回归拟合跟随法,文献[6]利用复杂的逆伽马函数拟合后,利用残差正态分布的异常检测,局限性必须检验证明残差符合正态分布才有效。文献[7-8]基于转矩利用复杂的线性拟合,然后进行残差阈值比较。文献[9]利用高斯滤波滤除部分噪声,然后采用近似积分法对脉宽曲线进行积分,再将积分面积和阈值进行比较做出是否防夹的判断,但是实际中不易定位脉冲的始末位置,同时脉冲周期是多变的,加之异常出现需要及时终止,一个正常的宽扁脉冲和一个异常的高窄脉冲的局部面积可能相等。类似算法[10]的复杂度比较适合硬件受限环境。通过对不同路况和时速下,每组3 000~5 000左右数据量,25组实测数据的分析研究,设计了一种更简单的算法——跟随周期均值显著化序列异常数据的学习算法,其中8组测试使用,17组为学习训练使用。
1 实验序列数据的原始特征
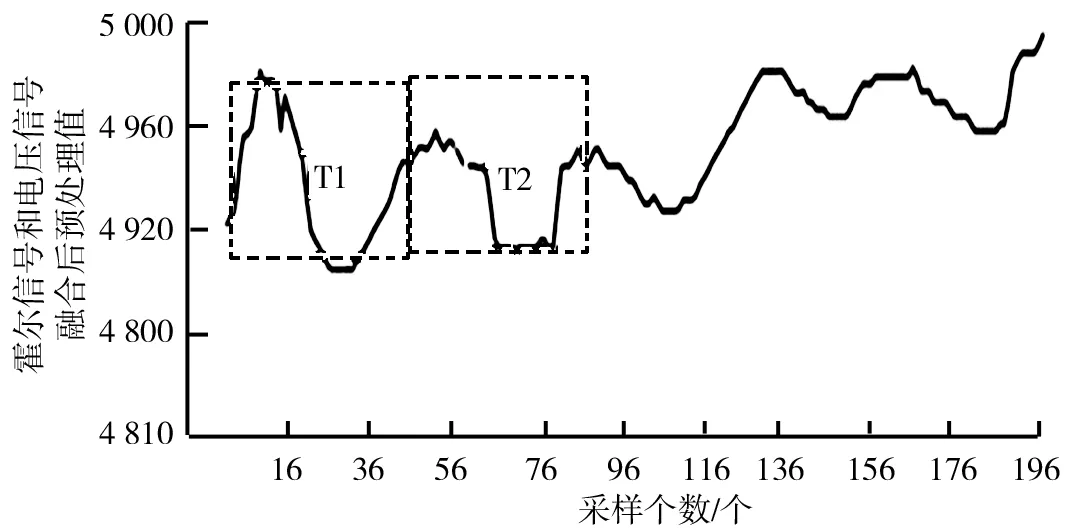
序列数据本身具有惯性、次序性、变化的正负性的特点。序列异常数据有分值异常、频率异常的情况,本算法针对此情况,以汽车车窗防夹的实际采集数据为研究基础,首先霍尔信号和电压信号融合成一组数据,实现数据平滑处理,处理后的序列数据图形如图1所示。由图1可知,序列数据正常情况下沿某一时段的均值上下震荡,同时均值上下移动,震荡周期有变化,异常数据明显高于正常数据,属于连续爬升过程,异常数据出现的判断是障碍物受力超出100 N,所以异常数据是一段初始爬升区域,是异常数据的局部,不会放任到最高值的出现。同时序列数据具有时效性,爬升阈值需参照临近的数据决定,具有跟随性,因此车窗防夹算法常常用回归拟合模型跟随检测,然后根据残差阈值做出判断。爬升阈值(残差阈值)如何设置是算法有效性的关键。如果跟随检测的相邻数据间值差异不显著,就易出现误判情况,因此提高跟随检测数据间取值差异是问题解决的重点。
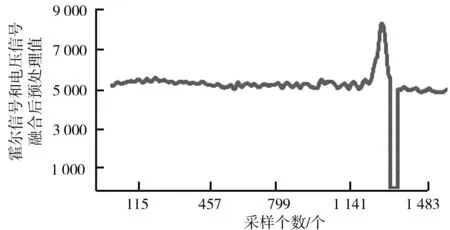
图1 原始数据预处理后的序列
2 跟随周期均值差值法的设计
2.1 算法周期选择分析
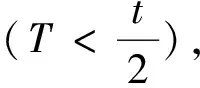
则相邻跟随周期均值的差值为:
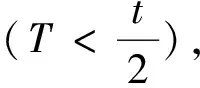
2.2 周期T和判断异常数据阈值的学习算法
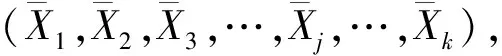
(1)跟随均值周期T′=c偏小/2;跟随周期均值显著化异常数据的标志,即阈值Dmax=0。
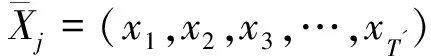
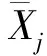
(4)在D中找最小值dmin。
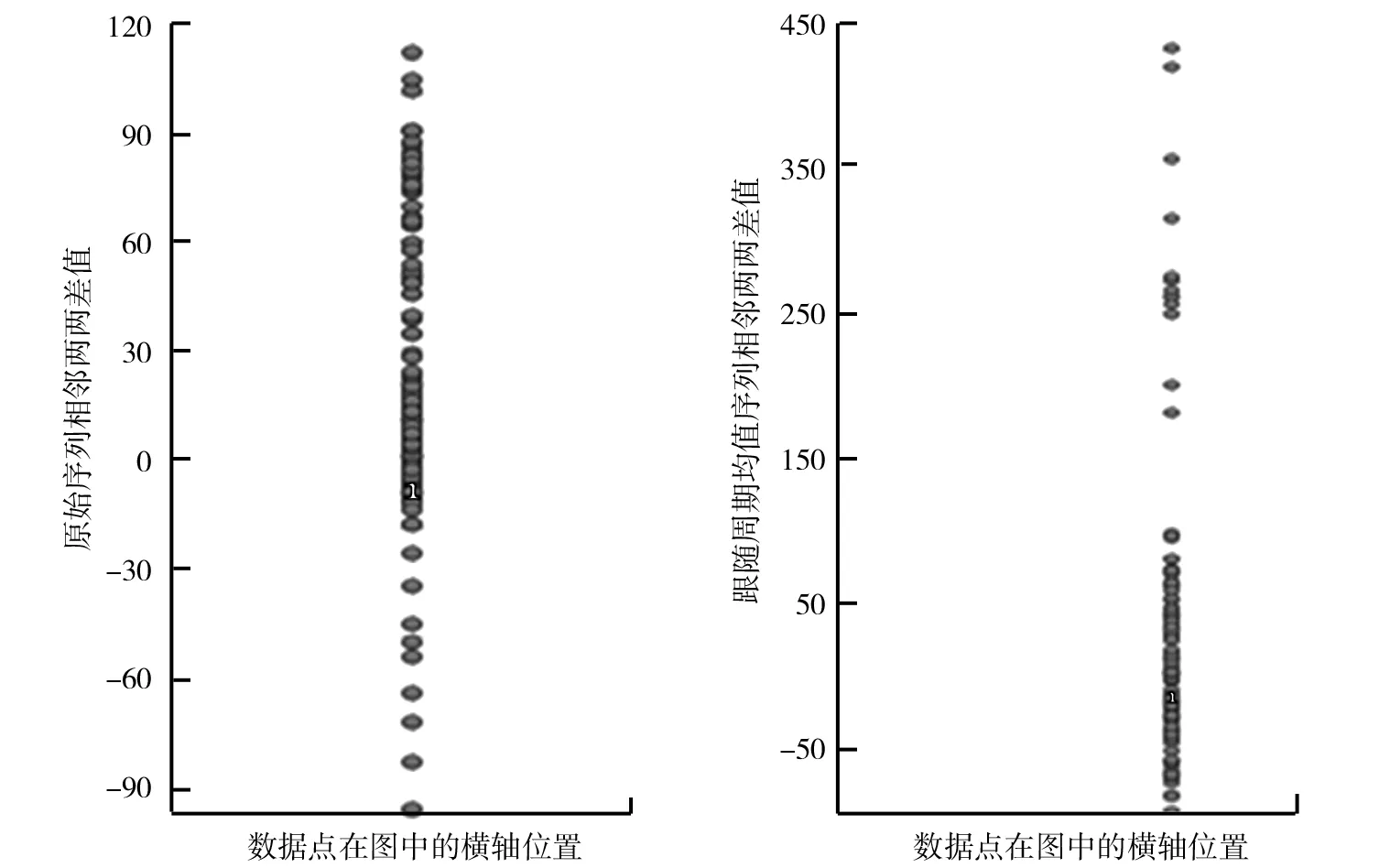
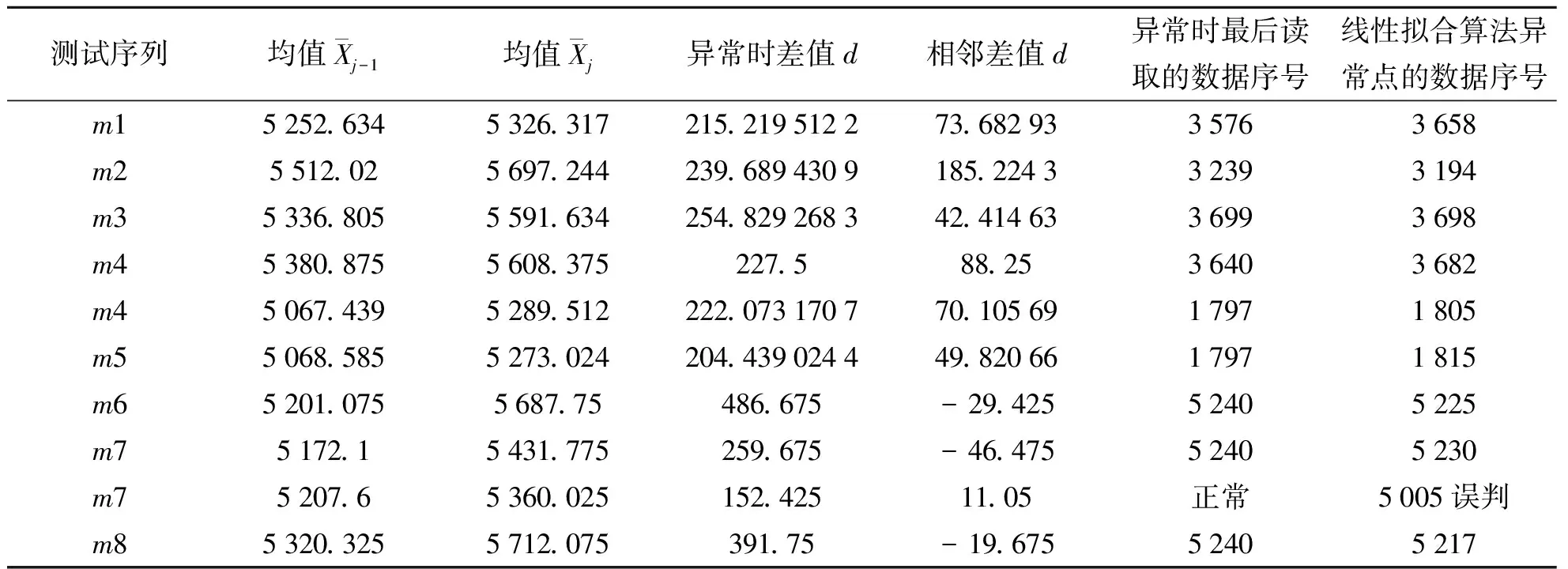
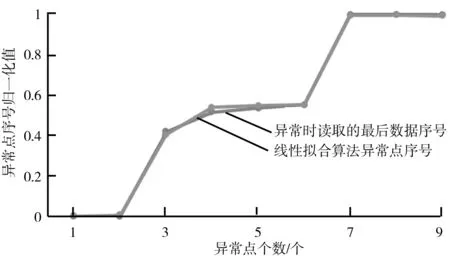
(5)T′=c+1;如果Dmax (6)重复(2)~(5)步,直到T′≥c偏大或T′>cα;其中cα为明显差异化的阈值。 图2 周期不稳定的序列以及跟随周期T 2.3异常检测设计 实验的数据处理、算法验证、数据图绘制工具为Grapher 12+R x64 3.5.0+eclipse 4.5.2。 直接分析序列相邻数据间差值,异常和正常数据间差异性不明确。随机抽取学习数据的10组数据,取包含异常数据区域的数据子序列(x1,x2,x3,…,x240),相邻两两求差值,分析差值取值分布,实验显示差值取值分布几乎连在一起成直线,没有明显的分层。10组结果中再次随机抽取一组其中含两个异常子序列的数据,其差值取值分布如图3所示。因此直接利用相邻数据间差异的相关特征判断异常产生,如拟合残差阈值判断异常的方法[7-8],极易出现误判。 图3 相邻数据间差值分布 图4 相邻周期均值差值分布 每组数据中至少含有两类变化性的数据的一种:障碍物阻力,必须防夹;对于不同速度、路面等引起的震动阻力不应防夹。测试结果与线性拟合算法进行了对比,8组测试序列中防夹点出现时的相关数据如表1所示。 数据显示本算法异常点的检测率为100%,而线性拟合算法出现了一次误判;与线性拟合算法的灵敏度相当,如图5所示。当障碍物固定在车窗某处时(测试序列m6、m7、m8),本算法的异常定位很稳定,具有简单鲁棒的特点,而线性拟合算法受外界速度、路况的干扰。 表1 防夹点出现时的相关数据 图5 与线性拟合算法的灵敏度对比 对于取值异常的序列数据,跟随周期均值法有显著化异常数据的效果,有效地提高了异常检测的正确率,降低了误检率,同时对外界干扰抵抗力良好,异常定位稳定。具有简单有效、鲁棒性的特点,对于实时监测,硬件受限的应用场景尤为适宜。对于多维数序列数据异常检测的效果有待验证,需要深入研究。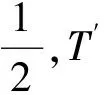
3 学习和测试结果分析
3.1 学习结果分析
3.2 测试结果分析
4 结语
