有侧压混凝土动态劈拉力学性能试验研究

， ， ， ，，竹君

(1.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002; 2.三峡大学 土木与建筑学院，湖北 宜昌 443002)

1 研究背景

准确认识混凝土动态劈拉力学性能是决定结构动力设计安全度的核心问题之一，对于实际工程的抗震、防爆以及安全评价具有重要意义，对它的理论研究需要不断深化与拓展。

Lv等[1]通过分析波形曲线的变化趋势得出霍普金森压杆试验中的混凝土变形与破坏规律。Erzar等[2]采用数值方法模拟了混凝土结构动态荷载作用下的响应。Feng等[3]发现了不同应变速率下导致混凝土劈拉强度增长的主要因素。吴彬等[4]基于ROC曲线理论分析了混凝土劈拉破坏损伤界点所对应的应力水平。王国盛等[5]将S准则中满足率效应规律的混凝土单轴强度发展成为多轴动态强度准则。胡伟华等[6]建立了不同应变速率下混凝土劈拉加载应力及同步声发射参数与时间的对应关系。王孝政等[7]发现混凝土动态劈拉强度与应变速率的对数呈线性关系，且混凝土吸能能力随应变速率的增大而增大。邹三兵等[8-9]利用声发射技术分析不同级配混凝土、自然状态与饱水状态混凝土在劈拉破坏全过程中的能量释放特性。梁辉等[10]基于Weibull和Lognormal统计分布理论构建出混凝土材料分段式率型损伤本构模型。

但是由于实际工程中梁、柱等构件常处于二轴或三轴应力状态，所以之前的大量试验并不能完全真实地反映混凝土材料的应力状态[11]。本文通过对不同侧压力作用下的混凝土动态劈拉试验现象进行研究，并构建改进的Mazars劈拉本构模型对混凝土动态劈拉全过程进行拟合验证，以期更深层次地分析混凝土动态劈拉破坏机理。

2 试验内容

2.1 试验设备

本文试验设备选用三峡大学与长春朝阳实验仪器有限公司联合研制的10 MN多功能动静力三轴仪电液伺服系统，如图1所示。

图1 试验设备Fig.1 Test equipment

该设备可实现3个方向加载，竖向最大静力10 MN，最大动力5 MN，水平向最大静力为5 MN。竖向油缸最大行程400 mm，水平活塞最大行程为200 mm。加载可通过负荷、变形、位移等加载方式控制，并且能够实现实时采集数据及存储、处理试验数据。

2.2 试件制备

本文试验采用边长300 mm的立方体混凝土试件，使用P·O 42.5普通硅酸盐水泥，拌合水为可饮用自来水，细骨料为细度模数为2.3的天然河砂，粗骨料为5～40 mm的连续级配碎石。依据C30强度等级进行配合比设计，具体配合比如表1所示。

表1普通混凝土配合比
Table1Mixratioofordinaryconcrete

材料用量/(kg·m-3)水水泥细骨料粗骨料水灰比17535067012500.5

试件制作时采用2次投料法，第1次投料水、水泥，搅拌3 min；第2次投料粗骨料和细骨料，搅拌5 min。搅拌完成立即装模，然后用振捣棒振捣成型。静置24 h后拆模，并立即放入标准养护室养护28 d。

2.3 试验过程

试验过程分为4个步骤：

(1)试验前准备。放置试件时选择相同编号的非浇筑面，对选定加载面的试件，用三角尺和铅笔做出试件中心线，然后将试件放入劈拉试验钢垫条上，保证试件中心线与钢垫条中心线重合。

(2)预加载。试验预加载大小为20 kN，分2步完成，先以变形加载控制荷载大小为10 kN，保持稳定后再加载至20 kN，荷载加载完成后，松开劈拉夹具固定装置。

(3)正式加载。首先加油压，之后发送侧压加载指令至侧向力加载完成，再立即竖向加载。试验加载采用的是位移控制，同时采用变形数据作对比参考。

(4)卸载及后续处理。卸载阶段稳定卸载，使试件保持破坏时原样，清理残渣及试件，检查仪器运行状态是否良好，以保证试件的有效性。

3 应变速率对有侧压混凝土劈拉力学性能的影响

3.1 应变速率对有侧压混凝土劈拉强度的影响

根据《普通混凝土力学性能试验方法标准》(GB/T 50081—2002)[12]以及《水利水电工程岩石试验规程》(DL/T 5368—2007)[13]中相关规定，得到混凝土立方体试件劈拉强度ft计算公式为

ft=(2P)/(πbc2) 。

(1)

式中:P为混凝土劈拉破坏荷载;bc为试件边长。

图2 不同侧压力下混凝土劈拉强度与应变速率的关系Fig.2 Relationship between splitting tensile strength and strain rate of concrete under different lateral pressures

从图2可以看出:侧压力的存在增大了混凝土劈拉强度；2种侧压力作用下，混凝土劈拉强度都是随着应变速率的增大而增大，说明侧应力作用下混凝土劈拉强度仍存在率效应。

侧压力的存在使混凝土试件能够更好地固定在平台上，在劈拉加载过程的开始阶段，劈拉条压实作用更容易实现对中，使得混凝土沿随机薄弱面开裂破坏可能性减小，进而侧压力的存在减小了试验数据离散性，使得相同应变速率量级下混凝土劈拉强度增长幅度更接近。

3.2 应变速率对有侧压混凝土劈拉弹性模量的影响

参考过镇海[14]弹性模量的取值，本文取40%～50%极限荷载时的割线模量作为混凝土劈拉弹性模量，得到2种侧压力下混凝土动态劈拉弹性模量E，如图3所示。

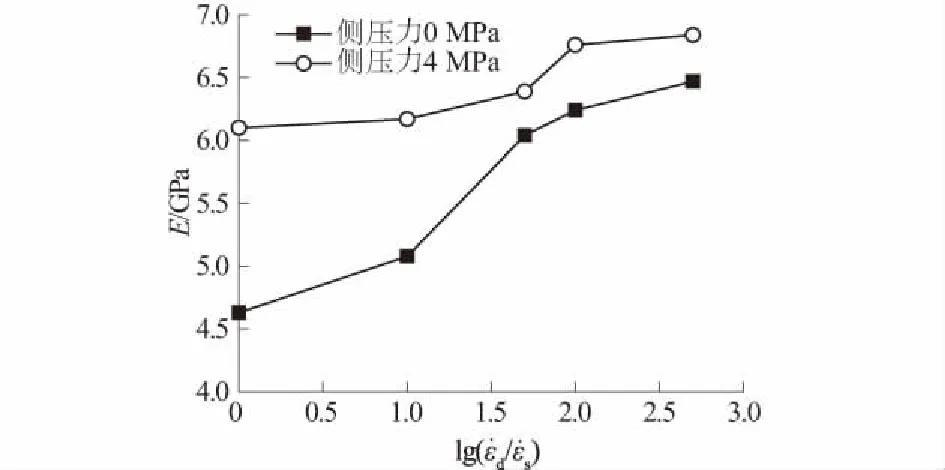
图3 不同侧压下混凝土动态劈拉弹性模量与应变速率的关系Fig.3 Relationship between dynamic splitting tensile modulus of elasticity and strain rate of concrete under different lateral pressures

由图3可知，2种侧压力下混凝土劈拉弹性模量均随应变速率的增大而增大，侧压力的存在也提高了混凝土劈拉弹性模量的大小，并使其率敏感性有所降低。这是由于侧压力的存在增强了混凝土试件的侧向约束，保证了混凝土试件的对中劈拉，使得试验结果稳定性更好。

4 侧压力对混凝土劈拉力学性能的影响

4.1 侧压力大小对混凝土劈拉强度的影响

对2种应变速率下的混凝土进行不同侧压力下的劈拉加载试验，根据式(1)计算得到相应条件下劈拉强度，如图4所示。

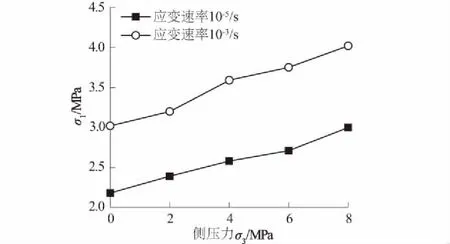
图4 混凝土劈拉强度与不同侧压力的关系Fig.4 Relationship between splitting tensile strength and lateral pressure of concrete

2种应变速率下混凝土劈拉强度都是随着侧压力增大而增大。这是由于侧压力的存在，抑制了试件的横向变形，使混凝土沿粘结薄弱界面开裂破坏的可能性减小，从而阻碍了裂纹尖端混凝土材料连续损伤的集中化发展，最终导致混凝土劈拉强度的增大。此外，侧压力为弹性荷载，理论上并不影响混凝土受力特性，改变了其应力场的变化趋势。

2种应变速率下混凝土劈拉强度增幅规律如表2所示。

表2 混凝土劈拉强度随侧压力增长幅度Table 2 Growth rate of concrete’s splitting tensilestrength with the increase of lateral pressure

从表2相邻列数据的差值可以得出，2种应变速率下混凝土劈拉强度都是在侧压力为6 MPa时邻近增幅(相邻2种侧压力下劈拉强度的变化幅度)出现一个最小值,此时侧压力的大小相当于混凝土设计强度的20%，这表明侧压力水平的变化会改变试件的应力场，进而对混凝土劈拉强度产生较大影响。

对2种应变速率下混凝土劈拉强度与侧压力的关系进行拟合，给出定义关系式为

σ1=aσ3+b。

(2)

式中：σ1表示动态劈拉强度；σ3表示混凝土侧压力大小；a和b均为材料相关参数。

根据式(2)利用最小二乘法对2种应变速率下混凝土劈拉强度与侧压力的关系进行拟合，得到拟合相关参数如表3所示,表中R2为决定系数。

表3混凝土动态劈拉强度拟合参数值
Table3Fittingparametersofconcrete’sdynamicsplittingtensilestrength

应变速率/s-1abR2拟合公式10-50.102.180.96σ1=0.10σ3+2.1810-30.133.010.95σ1=0.13σ3+3.01

2种应变速率下混凝土劈拉强度与侧压力线性拟合决定系数都≥0.95，说明混凝土劈拉强度随侧压力增大符合线性增长的规律，式(2)拟合效果很好，由此可以根据得到的拟合公式预测随侧压力大小变化的混凝土劈拉强度。

4.2 侧压力大小对混凝土劈拉峰值应变的影响

试验得到相应的劈拉峰值应变如图5所示。2种应变速率下混凝土劈拉峰值应变均随侧压力的增大呈现出先减小后增大的规律。

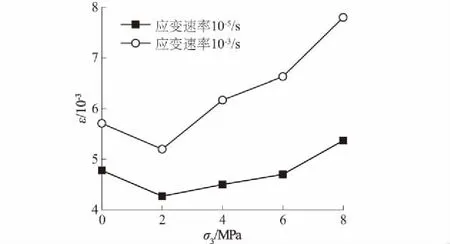
图5 不同侧压力大小与劈拉峰值应变的关系Fig.5 Relationship between lateral pressure and splitting tensile peak strain

这是因为：

(1)当侧压力较小时，对混凝土起到的仅是压实作用，约束了水平方向混凝土自由变形，对混凝土劈拉峰值应变起到了一定的削弱作用。

(2)随着侧压力的增大，试件断裂面将更多地直接出现在粗骨料上，降低了混凝土的脆性变形，提高了试件中骨料弹塑性变形的比例，增强了混凝土材料的吸能能力，使得有更多的应变能可以储存在材料内部，进而使劈拉峰值应变增大。

4.3 侧压力大小对混凝土劈拉弹性模量的影响

根据试验应力-应变曲线计算得到不同侧压力下混凝土劈拉弹性模量,如图6所示。

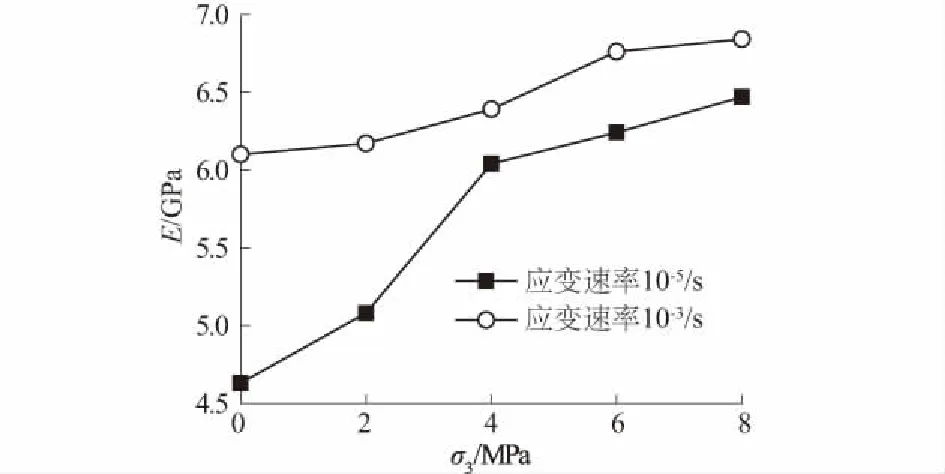
图6 混凝土劈拉弹性模量与侧压力大小的关系 Fig.6 Relationship between splitting tensile modulus of elasticity and lateral pressure of concrete

2种应变速率下混凝土劈拉弹性模量均随侧压力增大而增大，这主要是由于侧压力的存在使混凝土断裂面更多地直接出现在弹性模量更大的粗骨料上，并使混凝土材料更加密实，混凝土材料出现刚度增大的现象。增长速率先快后慢，低应变速率下混凝土劈拉弹性模量对侧应力更加敏感。从发展趋势看，混凝土劈拉弹性模量与侧压力大小近似呈线性变化规律，给出拟合方程为

E=aσ3+b。

(3)

式中：E为劈拉弹性模量；a，b为材料相关参数，拟合参数如表4所示。

表4 劈拉弹性模量拟合参数值Table 4 Fitting parameters of splitting tensile elasticmodulus

2种应变速率下，混凝土劈拉弹性模量与侧压力的线性拟合程度都很高，呈现很好的线性增长规律。劈拉弹性模量是与侧压力相关联的参数，可以根据得到的拟合公式(3)预测随侧压力大小变化的混凝土劈拉弹性模量。

5 应力-应变曲线模型研究

5.1 Mazars模型的改进

根据众多理论与试验研究[15]，发现具有软化段的Mazars模型可以反映混凝土受拉特征，给出具有软化段的Mazars模型为

(4)

式中：E0为峰值割线模量；AT和BT为对应曲线下降段形状控制参数;ε为混凝土劈拉应变;σ为混凝土劈拉应力；εpk为混凝土劈拉峰值应变; 0≤ε≤εpk和ε>εpk分别对应曲线的上升段和下降段。

根据梁辉等[16]的研究结果，采用非线性公式更能反映混凝土劈拉应力-应变曲线特点，故改进上升段曲线方程为

σ=(a+cε)/[εpk(1+bε)] 。

(5)

依据几何边界条件：①ε=0,σ=0；②ε=εpk,σ=σpk，代入式(5)可得

a=0，b=c/(σpkεpk)-1/εpk。

(6)

将式(6)中的a和b代入式(5)得到劈拉上升段应力-应变曲线方程为

(7)

Mazars模型可以准确地反映劈拉应力-应变下降段曲线，故保留Mazars模型曲线下降段方程。综上所述，改进后的混凝土劈拉应力-应变全曲线方程为

式中c为上升段形状控制参数，可以通过对应力-应变曲线拟合得到。

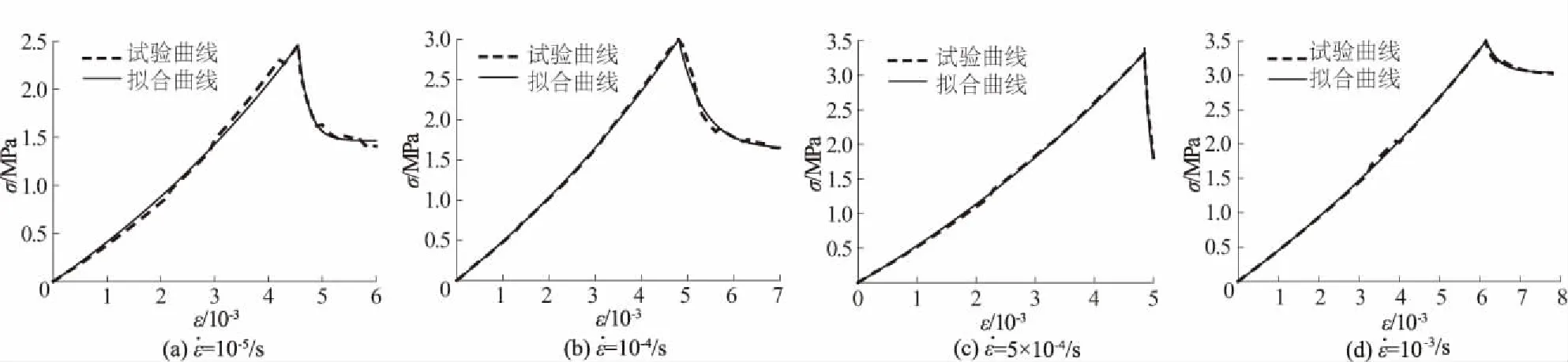
图7 侧压力为4 MPa、不同应变速率下混凝土单轴劈拉应力-应变拟合曲线Fig.7 Fitted curves of uniaxial splitting stress vs. strain of concrete at different strain rates under 4 MPa lateral pressure

5.2 不同应变速率下混凝土劈拉曲线拟合

图7中曲线的拟合决定系数均>0.95，可以看出改进之后的Mazars劈拉本构模型能够很好地拟合混凝土动态劈拉应力-应变曲线。拟合得到4 MPa侧压力下混凝土动态劈拉应力-应变拟合曲线上升段参数c值，如表5所示。

表5 4 MPa侧压力下劈拉拟合曲线上升段参数c值及其线性拟合相关参数Table 5 Values of c of the upward segment of fittedsplitting tensile curves and its linear fitting parametersat 4 MPa lateral pressure

侧压力为4 MPa下混凝土动态劈拉应力-应变拟合曲线下降段参数AT和BT的值如表6所示。

表6 劈拉拟合曲线下降段参数AT和BT值Table 6 Values of AT and BT of the downward segmentof fitted splitting tensile curves

参数AT和BT值与应变速率间并没有表现出明显的线性变化规律。试验曲线下降段并不是直线下降，这不代表试件仍有抗拉承载力，而是由试验加载夹具、试验设备等方面造成的。由此可以推断下降段参数AT和BT值是与试验工况及材料本身无关的量，其主要受试验条件因素的影响。

5.3 不同侧压力下混凝土劈拉曲线拟合

根据式(8)得到应变速率为10-3/s、不同侧压力下混凝土劈拉试验的拟合曲线，并与试验曲线对比，如图8所示。图8中试验曲线拟合决定系数均>0.90，表明该模型对不同侧压力下混凝土劈拉拟合效果都很好。由于下降段控制参数AT和BT值与试验工况无关，故仅对上升段参数c值分析，得到应变速率为10-3/s下混凝土劈拉应力-应变拟合曲线上升段参数c值及其线性拟合相关性参数，如表7所示。

由表7可得c=0.28σ3+1.96 ，参数c值与侧压力表现出较好的线性相关规律，综合考虑侧压力和应变速率2种因素得到拟合公式为

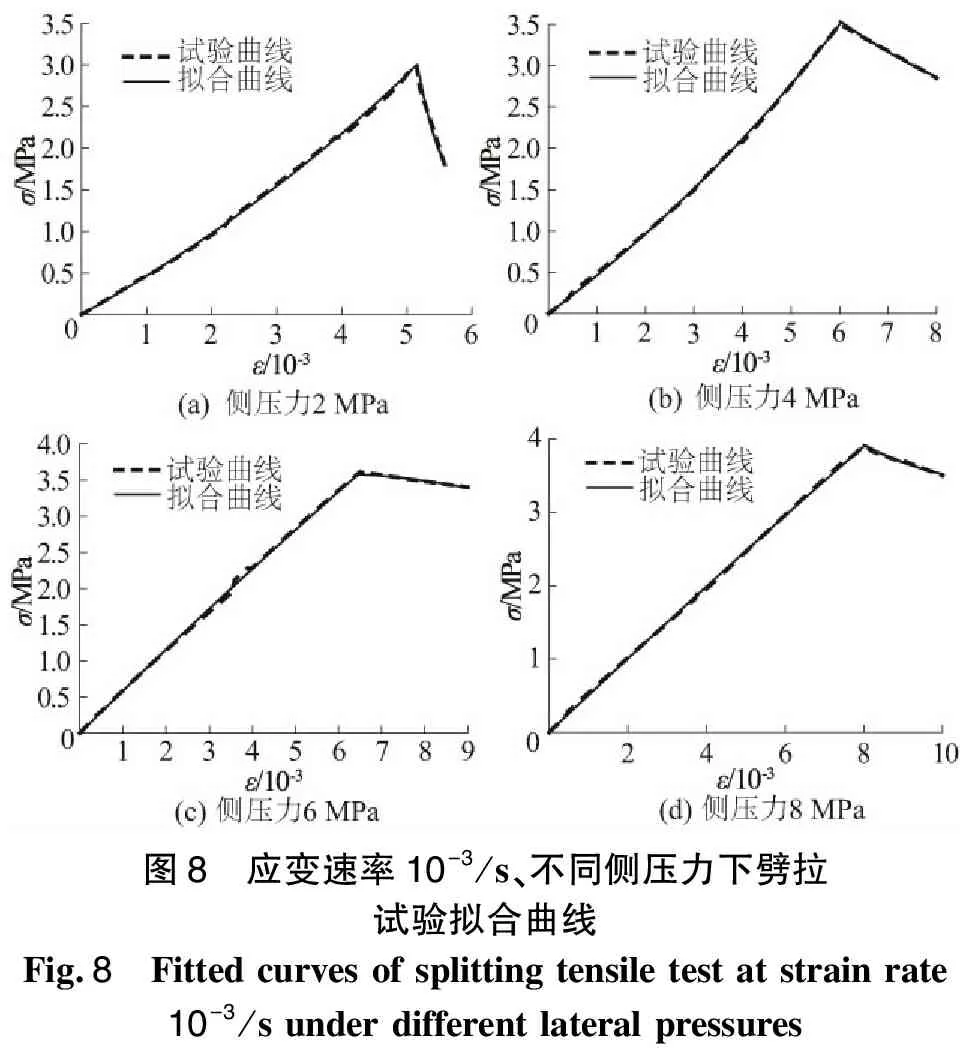
(9)

表7 应变速率为10-3下劈拉拟合曲线上升段参数c值及其线性拟合相关参数Table 7 Values of c of the upward segment of fittedsplitting tensile curves and its linear fitting parametersat 10-3/s strain rate

根据前文试验所获得的一系列上升段控制参数c值的数据，联立拟合求解得出m=0.567，n=0.338，b=0.36，其拟合决定系数为0.96，拟合公式可以很好地表现出c值的变化规律。同时可以通过进行更多的试验以获得相关试验数据，进而求解出更为全面准确的拟合参数m,n,b值。

6 混凝土劈拉本构模型适用性研究

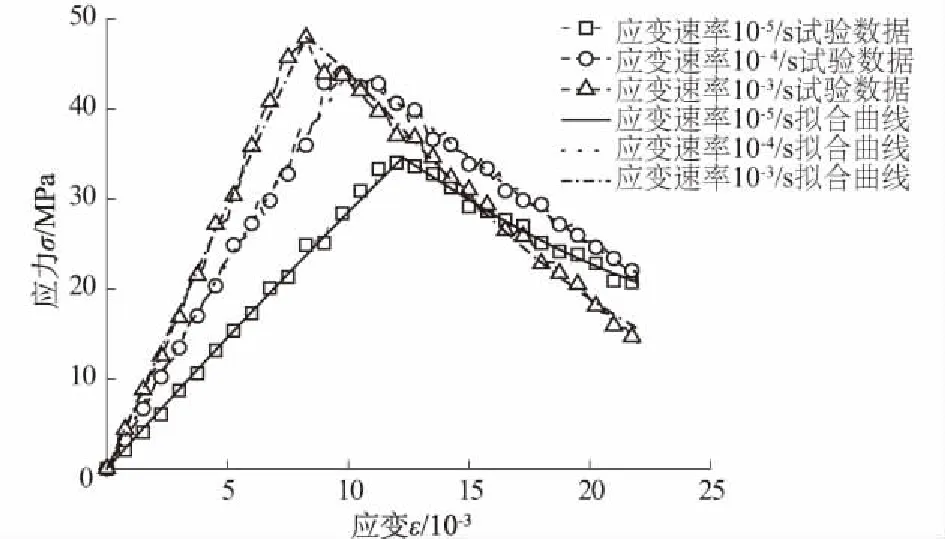
图9 劈拉试验数据拟合结果Fig.9 Fitted results of splitting tensile test data

贺誉[17]对Φ150 mm×300 mm(直径×高度)圆柱体试件进行了不同应变速率下的劈拉试验，根据本文构建的劈拉本构模型对其数据进行拟合，如图9所示。由图9可以看出，3种应变速率下的劈拉应力-应变曲线拟合程度都很高，说明该模型对其他学者进行的混凝土动态劈拉试验的数据适用性也很好。因为本文劈拉模型是混凝土抗拉应力-应变曲线研究的一部分，可以利用本文模型对混凝土直接拉伸试验进行研究。

陈育志等[18]采用钻芯圆柱体试件进行了混凝土直接拉伸试验，利用本文劈拉本构模型对其应变速率10-5/s和10-4/s下的试验数据进行拟合，拟合结果如图10所示。

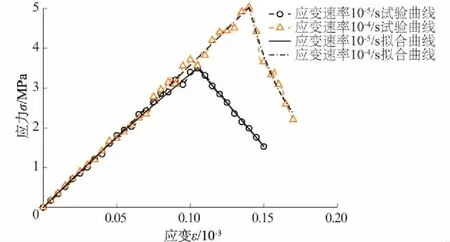
图10 直接拉伸试验数据拟合结果Fig.10 Fitted results of direct splitting tensile test data

可以看出该模型对2种应变速率下直接拉伸试验拟合效果都很好，说明该模型对混凝土直接拉伸试验也有很好的适用性。

7 结 论

(1)侧压力作用下，混凝土劈拉强度与劈拉弹性模量仍随应变速率的增大而增大。

(2)侧压力的增大会提高混凝土的动态劈拉强度与动态劈拉弹性模量，也会降低它们的率敏感性。混凝土动态劈拉峰值应变随着侧压力的增大呈现出先减小后增大的规律。

(3)通过对不同侧压力以及不同应变速率下的试验数据进行拟合比较分析，发现改进后的Mazars劈拉本构模型能较好地描述混凝土动态劈拉应力-应变曲线。将本文构建的劈拉本构模型与其他学者的试验数据进行对比，可发现该模型具有很好的适用性。

(4)Mazars劈拉本构模型中，上升段控制参数c值受应变速率与侧压力的双重影响。而下降段控制参数AT与BT值则与试验设备因素相关，与试验工况及混凝土材料本身无关。