中国省域高技术产业多元空间聚类

钮 亮， 代丽娟

(1.中国计量大学 经济与管理学院，浙江 杭州 310018；2.新疆大学 科学技术学院阿克苏校区，新疆 阿克苏 843000)

高技术产业作为知识密集型和技术密集型产业， 是科技创新的骨干力量， 其发展关系到整个国家的综合实力和竞争力。我国持续的经济增长为高新技术发展创造了良好的条件。高新技术发展得益于各个地区基础设施的不断建设和完善，并呈现出空间集聚现象。高技术产业集聚问题一直是学术界关注的热点，一般研究主要集中在高技术产业空间集聚[1-2]，高技术产业创新空间分布[3-4]和高技术产业空间演化方面[5-7]。不过涉及空间集聚现象的高技术产业处理的大多是单变量数据，但实际高技术产业区域的空间集聚往往依赖于多个变量的共同作用。尽管有些文献也处理过高技术产业多个变量的集聚[8-10]，但它们处理的都是非空间聚类。也有一些别的行业的多变量采用了空间聚集方法，但它们的空间集聚采用主成分和局部Geary系数结合的方法[11-13]。在主成分分析中，首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平，其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释，否则主成分将空有信息量而无实际含义。由于k均值聚类分析能够将相似的多变量数据归类成几种类别，而不失去均衡性[14]，也不存在主成分要求的累计贡献率问题，因此将可以利用k均值聚类分析的优点来改善主成分存在的问题。变量的空间自相关计算采用局部moran指数[15]，局部moran指数可以将空间依赖精确到每一个具体的单元，这为使用k均值聚类提供了数据支持。因此将k均值聚类和局部moran指数相结合探索高技术产业多变量聚类，识别出高技术产业热点区域、冷点区域，是研究问题的所在。

一、多变量空间聚类

多变量空间聚类的k均值和局部moran指数统计结合框架如图1所示。

基本流程为:(1)整理多变量数据为非空间多变量矩阵，对空间单元进行空间权重设定；(2)对多变量中每个变量做全局空间自相关测度，确保变量存在空间依赖；(3)对满足全局空间测度的变量进行局部moran指数转换；(4)对转换后的带有空间属性的变量进行k均值空间聚类，最优聚类数通过肘方法、轮廓线系数、Gap方法等多种测度手段的最优解来确定；(5)利用拟合优度测度带空间属性的k均值聚类与非空间k均值聚类的优势；(6)根据局部moran指数冷热点探测特性，测度多变量空间聚类后的冷热点分布。

基于局部moran指数的多变量空间聚类涉及到全局空间自相关，局部空间自相关，k均值聚类、方差拟合优度的理论知识，下面分别描述它们的相关理论。

图1 基于局部moran指数的多变量空间聚类

(一)全局moran指数

在进行多变量空间聚类之前，需要对每个变量先做全局空间自相关的检测，以评价观察到的数据值偏离空间无关这个零假设的程度。空间无关意味着相邻的空间互不影响，互不依赖。如果变量不存在全局空间自相关，那么多变量中纳入空间要素就没有意义，进而多变量的空间聚类也没有意义。是否变量存在全局空间自相关关系通过空间自相关全局莫兰指数(Global Moran's I)来实现[16]，其公式为：

(1)

全局moran指数评估所表达的模式是聚类模式、离散模式还是随机模式，它的范围在-1和1之间。越接近于1，空间正相关越强，接近0则不存在空间相关性，接近-1则表示空间负相关性越强。moran全局空间自相关是一种推断统计，因此要考察它的零假设情况。p值具有统计学上的显著性，且Z得分为正值，则拒绝零假设，属性高值集聚；p值具有统计学上的显著性，且Z得分为负值，属性低值集聚。如果p值越小，Z分数的绝对值越大，就可以越放心的拒绝零假设。p值以小于0.05为参照，Z值以小于-1.96或大于1.96的置信区间范围为参照。

(二)局部moran指数

全局空间moran相关性测度强调的是整个区域的均值空间依赖，它告诉我们空间是否出现了集聚或异常值，但并没有告诉我们在哪里出现集聚或异常值，如果要测度变量每个位置的空间依赖性，需引入局部测度指标，测度局部指标的方法包括局部moran指数，局部Geary，局部G检验和moran散点图等。目前用的最多的是局部moran指数，局部moran指数是用来测度每个位置与周围位置的空间依赖性，每个区域单元的局部moran指数描述该区域单元与周围显著的相似性区域单元之间空间集聚程度，它的公式如下[15]

(2)

对于任何一个空间单元i=1，2，…，n。正值Ii表示要素具有包含同样高或同样低的属性值的邻近要素，该要素是聚类的一部分。与之对比，负值Ii表示要素具有包含不同值的邻近要素，该要素是异常值。局部moran统计可以用来解释局部的不稳定性，也即局部偏离全局空间相关性的情况，实现识别“热点”的要求。为了检验局部moran指数的统计显著性，将局部moran指数进行Z得分转换，公式如下

(3)

Z分数为正数且通过显著性检验表示空间存在集聚性，空间集聚包括了高-高值和低-低值集聚。低-低值集聚为冷点集聚，高-高值集聚为热点集聚。如果Z值为负数，且数值较高，意味着该样点是个空间离散点。空间离散点包括高-低值和低-高值，其中高-低离散为孤立的个别热点[17]。一般情况下，Z得分在小于-1.96大于1.96的范围里是统计显著的，而在小于-1.645大于1.645上的统计接近显著[18]。后续变量的空间转换采用Z得分转换。

(三)k-means聚类

k-means聚类是在一个数据集中寻找子群或类的技术。在对数据进行聚类时，希望将相似性数据归在同一个类中。由于事先不知道数据的类别基础信息，因此k均值聚类属于无监督学习。k均值聚类度量对象相似性的距离测度有欧式距离、欧式距离的平方、切比雪夫距离、明可斯基距离、自定义距离等等，本文的重点是比较空间聚类对非空间聚类的改善程度，两种聚类方案选择的距离测度要求一样，所以选择常用的欧式距离来实现。算法为：①从样本点中随机选择k个点作为初始簇中心。②将每个样本点划分到距离它最近的中心点μ(j)，其中j∈{1,2,…,k}所代表的簇中。③用各簇中所有样本的中心点替代原有的中心点。④重复步骤②和③，直到中心点不变或达到预定迭代次数时，算法终止[19]。基于欧式距离的标准，k均值算法被描述为一个优化问题，通过迭代使得簇内误差平方和最小。公式如下

(4)

式中，μ(j)为簇j的中心点，如果样本x(i)属于簇j，则w(i，j)=1，否则w(i，j)=0。

k均值聚类要将观察数据分到事先规定好的k个类中，聚类最优数目k要提前确定。k均值聚类最优数目确定有多种手段，有KL方法、Scott方法、Marriot方法、Ball方法、silhouette方法、Gap方法等。 R语言中的NbClust包综合考虑了这几种方法可以实现对最优主题数的确定[20]。

(四)方差拟合优度

为了评测空间聚类方法的效度，遵循聚类内部要素要越具相似性且聚类之间要越具差异性的原则，选择方差拟合优度(GVF)来测度它的有效性。方差拟合优度(GVF)是评价聚类精度的有效方法[21]，公式如下

(5)

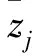
二、中国省域高技术产业多元空间聚类

(一)数据收集

为了测度中国省域高技术产业的多个变量的集聚情况，首先要选择能够代表高技术产业的变量。对于能够代表高技术产业发展的变量，目前学术界还未达成共识。学术界一般都集中在新产品值(NPO)[22]、专利申请数(PAT)[23]、省份高技术产业的R&D经费内部支出(ERD)和R&D人员全时当量(HRD)[24]方面，但研究的取向都以单一变量为主，对于这些变量共同作用的区域特征没有深入讨论。因此为了考察中国高技术产业创新产出的多变量空间聚集特征，变量选择以这4个变量为主。数据来源为中国高技术产业统计年鉴2013—2017年中的数据。

为了进行空间探测，针对4个变量所在的31个省市自治区构建空间权重矩阵，利用GeoDa软件生成 “车相邻”空间权重矩阵。按照“车相邻”邻近规则，海南省没有边界相邻的邻居，如果空间权重矩阵中空间单元的邻居数为零，在后续分析中会造成一些麻烦。为了避免这种情况，可以将海南省的邻居人为设定为距离较近的广东、广西。为保持空间权重矩阵的对称性，需要给广东、广西增加一个邻居海南[25]。

(二)四变量的空间自相关检验

经济数据大多数都是偏态分布，因此为了计算各个变量的全局moran指数情况，需要通过描述性统计观察数据的离散情况，以便于判断是否对数据进行对数化处理来消除偏度。高技术产业四种变量的描述统计结果见表1。

表1 省份创新活动主要变量的描述性统计

表1显示了2013—2017年期间，31个省份每年的高新技术产业数据描述性结果。从列角度看，中国高新技术产业的创新活动水平呈现递增趋势；从行角度看各省份的创新活动水平差异较大，表现为各指标的变异系数均大于1，在1.6到3.4之间，说明数据有一定的离散程度，需要通过取对数的形式处理这些数据。对数化处理后四种变量的空间集聚呈现的效果通过对它们进行全局moran指数、z值和p值判断来考察，见图2。

图2 空间相关性测度

从图2(a)可以看出,2013—2017这5年以来，PAT,NPO,ERD,HRD的moran指数大于0.05，存在一定的空间正相关性。由于全局moran属于统计量，需要根据p值和z值检验其零假设情况。其中检查p值见图2(b)，四个高新技术变量的p值均远远小于0.05，说明它们统计上存在显著性。z值结果见图2(c)，四个变量的z值都大于1.96，说明各省指标的聚集性存在统计学意义上的显著性，空间相关性结论比较可靠。

(三)带空间属性的k-means聚类

依照多变量空间聚类的要求，将对数化的PAT,NPO,ERD,HRD四个变量带入到公式(3)中，经过计算形成新的带空间属性的31行4列矩阵。然后对这个矩阵利用公式4中的算法进行聚类。最优聚类主题数通过R语言的NbClust包实现。NbClust包定义了Marriot方法、Ball方法、silhouette方法、Gap方法等几十个评估指标，然后聚类数目从2遍历到15。观察各种指标产生的最优聚类数，最后选择指标支持数最多的聚类数目为最佳聚类数。结果见图3。

图3 最优聚类数

从图3中可以看到，有9个指标支持最佳聚类数目为3，6个指标支持聚类数为2，所以该方法推荐的最佳聚类数目为3。为了观察多变量空间聚类的效果，先将k=3的k均值算法应用于普通属性的PAT、NPO、ERD、HRD变量，再将k=3的k均值算法应用于经过局部moran指数转化的PAT、NPO、ERD、HRD。然后用方差拟合优度(GVF)测度它们的聚类效果，并对两次产生的聚类结果进行比较，结果见表2。 从表2中可以发现，在考虑了空间要素后，各个类别的聚类观察值的GVF都有所提升，说明空间聚类较好地改善了传统非空间k均值聚类。

表2 非空间k均值聚类与空间k均值聚类的GVF比较

空间聚类不仅比传统聚类在聚类效果上有了提升，而且还可以判断所聚区域的冷热点集聚情况。方式是观察各个变量在不同聚类中的Z得分情况，参考每个空间聚类中的Z得分最大值、均值、中位数来判断多变量空间聚类的热点、冷点以及无空间相关性的分布。Z最大值大于1.645为接近热点聚类，大于1.96为热点聚类。而在-1.645到1.645之间的空间分布呈现随机性。小于-1.96的为冷点聚类。受篇幅的限制，我们选择2017年数据观察它聚类和冷热点分布情况，结果见表3。

2017年中 Cluster1中的省市自治区是：上海、北京、天津、安徽、山东、广东、广西、江苏、江西、河北、河南、浙江、湖北、湖南、福建、重庆，它们这些区域根据Z值的情况可以判断为趋近热点区域，之所以说是趋近热点区域是因为Z最大值超过了1.96，而均值小于1.645，说明这些区域的高新技术发展迅猛，取得了非常好的成果，在地图上呈现为蓝色。Cluster2中的省市自治区是云南、四川、新疆、甘肃、西藏、青海根据Z值的情况可以判断为冷点区域，说明这些区域的高新技术发展缓慢，没有什么好的成果发展出来，在地图上呈现为红色。表现不是太明显的Cluster3中的省市自治区是内蒙古、吉林、宁夏、山西、海南、贵州、辽宁、陕西、黑龙江。这部分的高新技术的发展呈现随机性分布，在地图上呈现为灰色，聚类具体结果见图4。空间多元聚类不仅探测了冷热点分布，就聚类的准确性而言也较传统聚类为好。按照普通聚类情况，图4(a)中灰色部分里没有辽宁省，而在图4(b)中辽宁省、黑龙江、吉林归在了一起，这显然是比较合理的，因为这三个省份都处于东北经济带范畴，辽宁无论是地缘还是经济形态都和浙江、江苏这些省份不同，因此归到图4(a)中的Cluster1这个聚类是不合适的。图4(b)中Cluster2红色版块的甘肃、四川、新疆、青海、西藏、云南高新企业集聚显然是合理的，因为它们基本处于西北边疆地区，以发展能源型企业为主，而高新技术的重视程度不够，这就比图4(a)中Cluster2仅包含西藏和青海两个地方要更准确。因此从图4(a)、图4(b)集聚来看，空间k均值聚类要比传统k均值聚类更为合理。当一些区域形成空间集聚时，说明这些区域的新技术产业在专利申请数、新产品值、R&D经费内部支出和R&D人员全时方面是相近的。

表3 2017年不同空间聚类中各个变量Z值情况

图4 传统多变量聚类和空间聚类

三、结论

尽管空间聚类方法已经在高技术产业中有了相关的应用，但是它们都集中在单变量领域，而对多变量的空间聚类中讨论不多。带空间的k均值聚类不但能够完成无监督聚类，提升聚类精度，而且还能对形成的聚类进行冷热点判断，是对常规聚类方法的一个改进。但空间聚类的前提是所观察变量要接受moran全局和局部的检验，符合空间依赖条件的变量采用空间聚类才是有效的。本文将局部moran指数空间统计和k-means结合起来进行高技术产业区域集聚研究，是空间多变量聚类的尝试性研究，还有一些问题有待进一步讨论。

(1)局部moran指数统计受它邻居数量和这些邻居空间统计的交互影响，这些影响是通过空间权重矩阵来表达的。由于局部moran指数统计的空间权重设置通过“车相邻”构建的，只考虑了与其相邻的要素的权重设置，有时候空间权重的设置还需要通过距离权重来设置，这样可以照顾到非相邻但却因为经济和社会因素相近的其他区域的空间依赖影响。例如今后高新技术产业多变量空间聚类权重可以根据专利申请数、新产品值、高技术产业的R&D经费内部支出，高技术产业R&D人员全时当量相似的区域的距离作为设定权重的标准。

(2)可以考虑其他局部空间自相关，例如局部G检验、局部Geary系数和k均值组合实现的多变量空间聚类，将其与局部moran指数和k均值聚类产生的结果进行比较，观察它们聚类的不同效果。

(3)传统的k-means聚类根据数据的距离测度(本论文选择欧式距离)完成类属划分，无法区分热点数据和冷点数据，而空间聚类方法由于加入了局部moran指数素，能够观察各个变量在不同聚类中的Z得分情况，通过选取每个空间聚类中的Z得分均值来判断多变量空间聚类的热点、冷点以及离散分布情况，从而使得产生的聚类结果具有冷热点分布效应。

(4)基于点的空间聚类方法要求足够的样本来达到分析的稳健结果。经验法则考虑30个样本为最低门槛，为了k均值聚类的稳定性，可以考虑采用重抽样技术来增大样本量满足稳健性要求。

(5)本文所处理的空间单元是以省域空间尺度为主的，还可以将这种方法扩展到市县级空间尺度 ，例如选择长三角市县一级的高技术产业区域，对其进行多变量的空间集聚，以便寻找哪些区域是相似的和哪些区域是冷热点分布的。

以上提到的改进地方有待做进一步研究。