贝叶斯倾向性评分在R软件中的实现*

四川大学华西公共卫生学院流行病与卫生统计学系(610041) 杜春霖 李宓儿 王 菊 李晓松 刘元元

常规的混杂因素校正方法包括分层、匹配或回归分析，但当混杂因素较多时，均不再适用。倾向性评分(propensity score,PS)是解决此类问题的有效工具，它将个体所有协变量信息综合为接受某种处理的条件概率，再利用此概率对样本进行匹配、分层或加权等，可达到“事后随机化”的效果[1]。2000年Imbens等人定义了广义倾向性评分(generalized propensity score,GPS)，将传统的PS理论扩展到处理因素为多分类及连续型变量的情形[2-3]。

随着PS方法的广泛应用，逐渐暴露出传统理论的一些缺陷，如：默认PS值固定，忽略了其不确定性，影响处理效应估计的准确性[4]；采用logistic等回归模型估计PS时，模型假设有时无法满足[5]；在估计模型参数时，无法利用先验信息；没有处理缺失数据的有效手段等[6]。基于以上问题，国外学者提出了贝叶斯倾向性评分(bayesian propensity score,BPS)，可有效弥补传统方法的不足[4,7-10]。国内近年来已有部分学者开始研究BPS相关理论[11-13]，但如何实施BPS分析尚缺乏专门介绍。本文将结合BPS理论介绍如何应用R软件实现BPS分析。

方法原理

Rubin早在1985年就指出PS实际上是一个随机概率，在处理分配是强可忽略的前提下，PS是可测协变量的充分统计量，具有应用贝叶斯理论的条件。得益于计算科学的高速发展，贝叶斯统计得以广泛应用，而BPS理论也逐渐趋于成熟，以下按照BPS理论的时序发展介绍3类BPS方法。

1.“联合”BPS法(Bayesian Approach with Joint Likelihood of PS and Responses)

Hoshino在2008年首次提出了一种针对一般参数模型的拟贝叶斯估计方法，并与结构方程模型结合，用于处理潜变量模型等复杂问题[7]。McCandless等人和An先后在2009和2010年构造了BPS分层回归法，BPS匹配法与回归法[4,8]。以上方法均采用MCMC算法，利用PS条件下处理因素和结局变量的联合分布似然函数，同时估计出处理效应、协变量和PS前的回归系数。以McCandless的方法为例，建立两个logistic回归模型：

logit[Pr(Y=1|X,C)]=βX+ξTg(z(C,γ))

(1)

logit(Pr(Y=1|C))=γTC

(2)

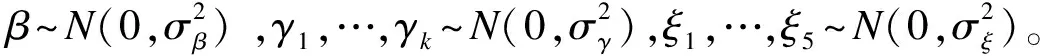
“联合”BPS法将PS估计和处理效应估计两个独立步骤对应的似然函数联立为一组似然函数，此时PS作为一个未知量，其后验样本将受到结局模型的“反馈”，这类反馈可能导致处理效应的错误估计。Gelman和Corwin等人均指出PS应当只反映研究设计，而不应包含任何处理效应或结局的信息[14-15]。因此，当结局变量和PS关系被错误建立时，“联合”BPS法的估计结果通常不准确。

2.“分半”BPS法(“Half-Bayesian” Approach for Propensity Score)

An在2010年的同一研究中提出了另一种“分半”BPS法可避免“模型反馈”的影响，该法采用贝叶斯logistic回归模型估计PS，而在利用PS估计处理效应时，则采用传统的OLS方法[8]。具体过程如下。

(1)构建协变量和处理因素的PS模型用于估计PS，即e(x)：

(3)

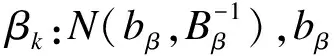
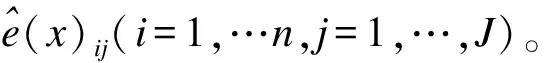
(3)构建PS、处理因素和结局变量的广义线性模型用于估计处理效应，以回归法为例：

Y=μ+γW+λe(X)+ε

(4)

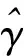
(5)

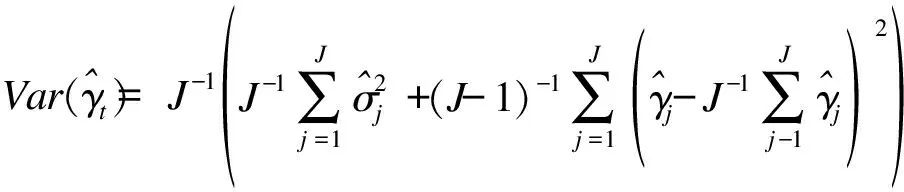
(6)

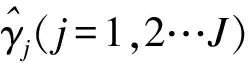
3.“分步”BPS法(Two-step Bayesian Approach for Propensity Score)

为克服“模型反馈”的问题，McCandless等人采用Lun提出的一种“切断反馈”技术对原方法进行了改进，其核心思想是将PS 模型参数的后验分布作为协变量纳入结局模型[9]。同McCandless等人想法类似，Kaplan和Chen进一步提出“分步”BPS法，该法第一步同“分半”BPS法，第二步则采用贝叶斯结局模型估计处理效应[10]。

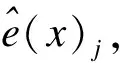
处理效应则通过γ的后验均值估计如下：

E(γ|W,Y,X)=E{E(γ|η,W,Y,X)|W,Y,X}

(7)

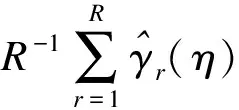
(8)

上式又可通过贝叶斯PS模型中η的后验样本均值估计得到，则：

(9)

γ的后验方差可通过下式求得：

Var(γ|W,Y,X)=

E{Var(γ|η,W,Y,X)|W,Y,X}+

Var{E(γ|η,W,Y,X)|W,Y,X}

(10)

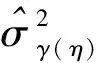
(11)

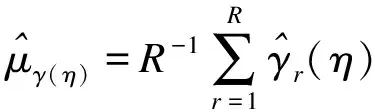
(12)

因此“分步”BPS法的处理效应方差估计值如下：

(13)

从(13)式可以看出处理效应的两部分变异，分别对应后验样本方差的均值，以及后验样本均值的方差，同时综合了PS和处理效应的不确定性。

模 拟

目前，“联合”BPS法可通过R Studio下载An编写的IUPS包实现。“分半”BPS法可借助MCMCpack包编程实现，而“分步”BPS法的函数包BayesPSA需通过本地文件下载和安装(链接：http://bise.wceruw.org/publications.html)。

本文数据仿照Chen和Kaplan研究中所用的模拟数据[10]。其中包含3个协变量(x1～N(1,1),x2～Poisson(2),x3～Bernoulli(0.5)) ，真实PS值计算如下：

(14)

通过比较e(x)i和Ui(U～Uniform(0,1))的大小，产生处理因素w(当Ui≤e(x)i时wi=1，Ui>e(x)i时wi=0)，结局变量y按下式生成：

y=0.4x1+0.3x2+0.2x3+0.5w+ε

(15)

其中，ε～N(0,0.1)，本例中样本量设为100和250。

BPS分析的具体过程如下(R代码可参考附录)：

(1)整合实际数据。本文数据通过模拟产生，真实处理效应预设为0.5。

(2)加载函数包，实现BPS分析。其中，IUPS包提供了“联合”BPS最邻近匹配和回归的函数，BayesPSA包可实现“分步”BPS最优匹配和分层法。“分半”BPS法以加权法为例进行了展示，读者可参考程序实现其他几种PS利用方式。

(3)将第2步所得主要结果整理为表1。由于“联合”BPS法中默认采用参数的无信息先验，为使结果具有可比性，在“分半”BPS法和“分步”BPS法中同样采用无信息先验。

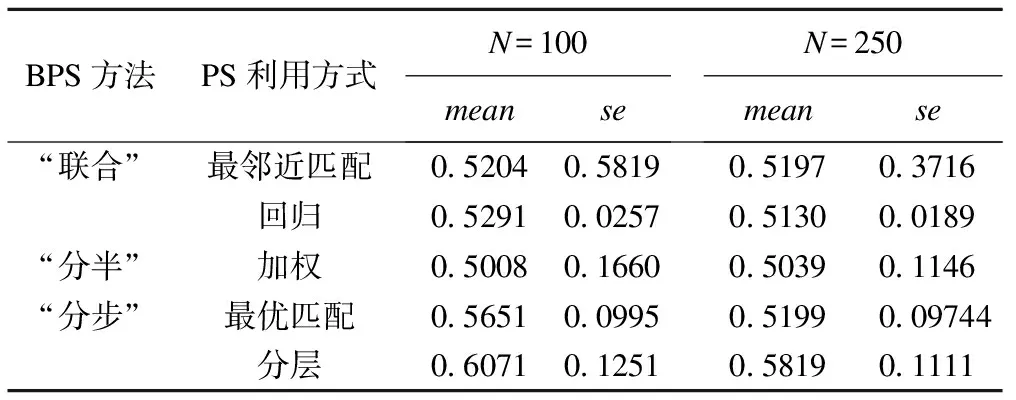
表1 BPS分析结果汇总表

从结果可看出“分半”BPS加权法偏倚最小，而“联合”BPS回归法的标准误最小，3种BPS法的处理效应估计效果均随样本增大而更优。值得注意的是，此处假设正确建立了PS模型和结局模型，因此“联合”BPS法的结果很少受到“模型反馈”的影响。对于本文BPS分析的结果，在实际应用中会受到先验精度、PS利用方式以及模型不确定性等因素的影响，因此并不具备代表性，有待更为系统的模拟研究以探讨这3类BPS方法的适用条件。

讨 论

PS 方法作为一种处理观察性研究中混杂偏倚的有力工具，已被广泛应用于流行病学、心理学和社会学等多个领域。 PS理论从提出到目前已有30年的历史，BPS作为其最新理论成果，具有广阔的应用前景。BPS考虑了倾向分值的随机性，可以更精确地估计倾向分值，并有效利用先验知识，使结果更加真实可靠。此外，BPS可与复杂模型相结合处理相应的实际数据，尤其适用于小样本情形[4]。

本文分别介绍了“联合”BPS法、“分半”BPS法、“分步”BPS法，其中“联合”法必须是在正确建立结局变量和PS模型的前提下，结果才具有参考价值，而不同学者提出的联合分布似然函数不尽相同，尚无相关研究论证孰优孰劣。其次，有关先验信息的设定仅Chen和 Kaplan在“分步”法中进行过讨论，主要比较了无信息先验和精确先验在不同先验精度下对结果的影响，其他形式先验的估计效果有待进一步研究论证[10]。最后，PS模型正确与否和好坏与否极大程度影响到结果的准确性和可靠性，将贝叶斯模型平均(Bayesian Model Averaging,BMA)应用至BPS分析，可一定程度上综合模型选择的不确定性，得到更加合理的效应估计[16]。

此外，BPS对于协变量的均衡效果以及BPS在多分类处理因素中的应用均是当前的研究热点[12,17]，读者可在实现简单BPS分析的基础上，进一步了解和掌握BPS的相关理论，推广其在实际数据分析工作中的应用。

附录：

###模拟数据

gendata<-function(size){

#产生自变量

x1<-rnorm(size,1,1);x2<-rpois(size,2);x3<-rbinom(size,1,0.5)

#计算倾向性评分

ps<-exp(0.2*x1+0.3*x2-0.2*x3)/(1+exp(0.2*x1+0.3*x2-0.2*x3))

#产生处理因素

u<-runif(size,0,1);w<-NULL

for(i in 1:size){

w[i]<-ifelse(u[i]<=ps[i],1,0)

}

#产生结局变量

e<-rnorm(size,0,0.1)

y<-0.4*x1+0.3*x2+0.2*x3+0.5*w+e

#产生数据

simudata<-data.frame(y,x1,x2,x3,w)

return(simudata)

}

data1<-gendata(100);data2<-gendata(250)

###联合BPS法

library(IUPS)

X<-as.matrix(data1$x1,data1$x2,data1$x3)

#BPS最邻近匹配(“ATE”代表平均处理效应)

bpsm(data1$y,data1$w,X,method=“BPSM”,estimand=“ATE”)

#BPS回归

bpsr(data1$y,data1$w,X)

###分半BPS加权法

library(MCMCpack)

#通过MCMC产生参数后验样本(burnin为“消火”次数，mcmc为迭代次数，thin为间隔长度，tune为Metropolis调整参数，，b0和B0分别对应服从多元正态分布参数的先验均值和精度)

poster1<-MCMClogit(w～x1+x2+x3,data=data1,burnin=1000,mcmc=10000,thin=10,tune=0.25,b0=0,B0=0)

beta<-poster1

#计算PS

gmodel<-glm(w～x1+x2+x3,data=data1)

mat<-model.matrix(gmodel)

bps<-matrix(rep(0,nrow(beta)*nrow(data1)),nrow=nrow(data1))

for(i in 1:nrow(beta))

{

temp<-mat%*%beta[i,]

bps[,i]<-exp(temp)/(1+exp(temp))

}

#构造加权函数(采用逆处理概率加权)

psweight<-function(y,ps,trt)

{

wt<-rep(0,length(ps))

wt[trt==1]<-1/ps[trt==1]

wt[trt==0]<-1/(1-ps[trt==0])

mod<-lm(y～trt,weight=wt)

return(c(summary(mod)$coef[2,1],summary(mod)$coef[2,2]))

}

#估计处理效应及其标准误

bwlm<-cbind(rep(0,nrow(beta)),rep(0,nrow(beta)))

for(i in 1:nrow(beta))

{

bwlm[i,]<-psweight(data1$y,bps[,i],data1$w)

}

mean(bwlm[,1])

sqrt(var(bwlm[,1])+mean(bwlm[,2]^2))

###分步BPS法

#计算PS (response和treatment分别用于指定结局变量名，处理变量名，treatment.success.level定义接受处理时所取变量值，vars为协变量名，prior.b0、prior.B0分别为先验均值和先验精度，mcmc.burnin为“消火”次数，mcmc.iter为迭代次数，mcmc.thin为间隔长度，mcmc.tune为Metropolis调整参数，method可选“BMA”，即贝叶斯模型平均。)

bps<-bpsa(data1,response='y',treatment='w',treatment.success.level=1,

vars=c('x1','x2','x3'),prior.b0=0,prior.B0=0,mcmc.burnin=1000,

mcmc.iter=10000,mcmc.thin=10,mcmc.tune=0.25,

method=c(“MCMC”))

#BPS最优匹配

bpsa.opt.match(bps,prior.b0=0,prior.B0=0,mcmc.burnin=1000,

mcmc.iter=10000,mcmc.thin=10,mcmc.tune=0.25)

#BPS分层

bpsa.strat(bps,prior.b0=0,prior.B0=0,mcmc.burnin=1000,

mcmc.iter=10000,mcmc.thin=10)