合成孔径雷达BP与FBP时域成像算法比较
2019-03-19陈家瑞
史 鉴,陈家瑞
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
合成孔径雷达(SAR)成像经过数十年的发展,主要形成了时域和频域两大类成像算法。主要的频域成像算法有距离多普勒(RD)算法[1]、ω-k算法[2]、调频变标(CS)算法[3]、极坐标格式算法(PFA)[4]等。时域成像算法主要有反向投影(BP)算法[5],以及基于BP算法的快速反向投影(FBP)算法等。
BP算法最初源于计算机层析成像技术,后经发展应用到医学CT成像等领域,美国科学家McCorkle最早将该成像技术引用到合成孔径雷达成像中。该算法的基本思想是以像素为最基本单位,将成像区域划分成网格,计算出每一方位时刻SAR平台的位置与每一个网格点(像素点)之间的距离,然后算出双程延时,再根据每个方位脉冲计算的双程延时进行反投影,得到每张层析图,最后再将所有的层析图进行相位补偿后相干叠加,得到最终的SAR图像。
雷达发射的电磁波照射到成像场景中,经反射得到目标雷达回波,回波信号经距离向脉压后,由于电磁波波前是弧形球面波,因此每一方位时刻距雷达平台的距离是变化的,该现象称为距离徙动,且距离徙动轨迹随目标散射点径向距离的不同而弯曲程度不同。BP算法通过逐点反投影成像,消除了距离徙动对成像的影响。虽然BP算法在数学原理推导过程中,没有经过近似处理,具有很好的精确性和稳定性;但是由于该算法对每一脉冲进行反投影,运算量大,消耗资源多,因此限制了其实际应用。
FBP算法先通过划分子孔径,在降低角域采样点数基础上对每个子孔径反投影成像得到角分辨率低的图像,然后再将子孔径低角分辨率图像逐级融合处理,得到高分辨率图像。FBP算法可以很大幅度减少运算量,提高了运算实时性,为BP SAR成像算法在实际工程中的运用提供了可行性。
1 BP成像算法
1.1 聚束SAR成像模型
聚束式SAR成像是一种常见的成像模式,该模式在成像时,可以根据需要,调整天线波束指向,实现对某一区域灵活的高分辨率成像。与其他SAR成像模式相比,在相同合成孔径长度时,聚束模式下,场景中的目标成像合成孔径时间比条带模式下更长,从而拥有更大的方位扫描角度、更高的方位向分辨率,打破了条带SAR下方位向分辨率受限的情况,并且在成像区域的选择上更具有灵活性。
如图1所示,假设雷达载机沿着X轴的方向上以速度v匀速直线飞行,高度为H,载机在Y轴上的坐标为ya。坐标原点O设在成像场景中心,R为合成孔径到成像场景中心点O的垂直距离,雷达载机在飞行时,天线中心的瞬时坐标为(xa,ya,H),点P(x,y,z)为成像场景中任意一点的坐标,Ra为点(xa,ya,H)到点P(x,y,z)的瞬时距离。
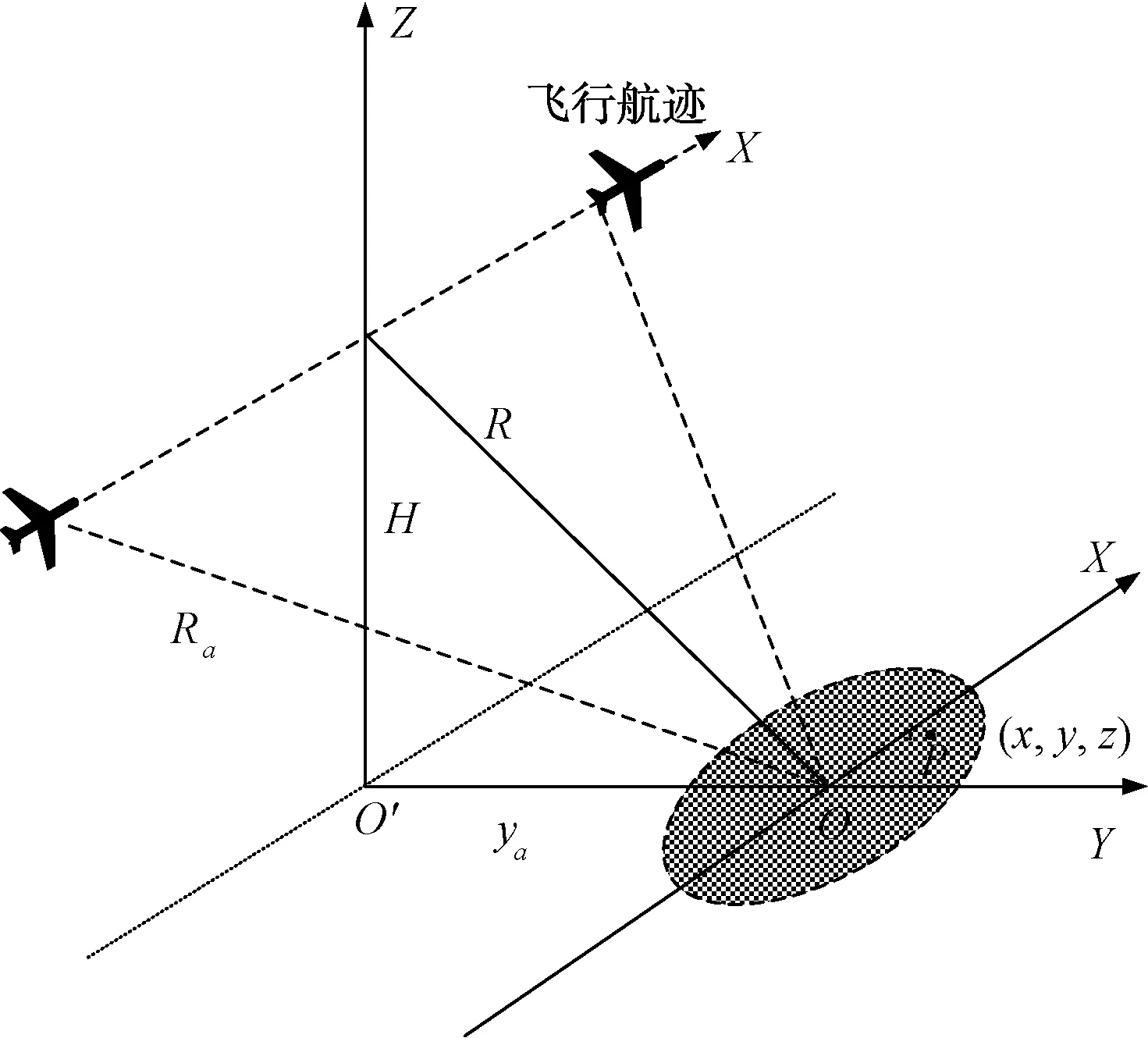
图1 聚束SAR空间模型图
1.2 BP算法原理分析
BP成像算法首先计算当前方位时刻雷达天线相位中心到成像网格中的每个像素点的瞬时斜距,根据斜距计算出双程时延,然后根据延迟时间,从脉压后的脉冲数据中求出成像区域中每个像素点对应的回波值,通过差值处理,形成一张层析图,每个脉冲反投形成一张层析图,最后将所有层析图相干叠加得出最后的BP算法SAR图像。具体实现步骤如下:
步骤1:将所有雷达回波脉冲脉压处理;
步骤2:计算成像区域每一像素点与每一脉冲时刻雷达天线的斜距,并将对应时刻脉压后的脉冲数据进行插值反投影操作得到一张层析图;
步骤3:参照成像区域中心点O,对每张层析图进行相位补偿;
步骤4:重复步骤3和4,每一脉冲反投影的图像数据沿方位时刻相干叠加,直至所有脉冲处理完;
步骤5:保存叠加数据,得到最终SAR图像。
1.3 BP算法运算量分析
BP算法处理步骤:首先脉冲压缩,然后反投影处理,最后以场景中心点为参考点进行相位补偿,其中运算量较大的为前2个过程。脉冲压缩主要包括复加、复乘以及复除;反投影过程主要包括复加和复乘。
假设雷达回波数据量为R×L(L、R分别为方位向和距离向数据量),成像区域像素点为M×N,采用频域脉冲压缩处理。
(2) 参考系数点乘运算:R×L次复除,R×L次复乘。
(4) 反投影运算:L×M×N次复加,L×M×N次复乘运算。
由以上分析可知,反投影中的插值运算次数就高达LMN次,如果有效地减少反投影操作的运算量,将大大提高BP算法的处理效率,FBP算法正是一种减少反投影操作运算量的快速BP成像算法。
2 FBP成像算法
2.1 FBP成像原理
根据成像模型,每一由天线位置反投影的回波数据在同一径向距离每圆弧上是相同的。对于相邻天线位置的A、B两点,在角度很小的一个扇形区域内,可以近似认为具有相同的一组同心圆,即可以以该扇形波束中心距离作为该区域的反投影距离,通过这种近似,降低角域采样点数得到角分辨率低的图像,然后再通过逐级融合,得到高分辨率图像如图2所示。

图2 极坐标系下误差图
2.2 FBP算法流程
FBP算法的处理过程可以看作新波束形成以及子孔径叠加的过程。假设合成孔径长度为L点(即方位向有L个脉冲),成像区域像素点为M×N。将L点长度的合成孔径长度通过k级级联划分形式表示为:
L=l1×l2×…×lk
(1)
式中:li为第i级处理过程中子孔径叠加后其个数减少的倍数。
为后续分析方便,假设L=M=N,l1=l2=…=lk=n,则新一级子孔径长度为上一级的n倍,同时新一级子孔径数目减少了n倍,新一级子孔径对应的波束数为原来的1/n,波束数目较上一级增加了n倍。
利用新波束的中心距离线来计算扇形波束的反投影数据。首先将该扇形区域中心距离线进行M点离散采样处理,计算出区域其他点与新孔径位置之间的距离,根据这M个点数据计算出该扇形区域反投影的数据,进行反投影插值处理,得到一组反投影数据。新一级的一个新波束的反投影数据与上一级n个旧波束反投影数据有关。为保证得到直角坐标下SAR图像,还需对新波束中心距离线上M个后向投影数据进行α倍的插值。
图3 第i级处理过程
图3所示为第i级处理过程,此时n=2,子孔径波束数量增为原来的2倍,子孔径数目减少为原来的1/2。新波束的反投影数据是通过对前一级两相邻子孔径对应的反投影数据经一系列合成运算获得的。
通过上述FBP算法处理流程,逐级处理,直至最后一级,最终得到像素点为M×N的高分辨率SAR图像。
2.3 FBP算法运算量分析
FBP成像算法在第一级过程中,新一级的子孔径数变为L/n个,并且通过原来n个旧波束形成一个新波束,波束的采样率为M,通过插值处理,得到该级处理最终所需要的像素点,设插值因子为α,则其运算量为:
(L/n)nnαM=nαN2
(2)
在第二级处理过程中,最初子孔径数量通过融合处理后减少为L/n2个,每个新的子孔径形成n2个新波束,波束采样率同样为M,同时每个新的波束通过上一级n个旧波束的数据形成,插值因子同样为α,则其运算量为:
(L/n2)n2nαM=nαN2
(3)
每一级子孔径合成的运算量均为nαN2,通过级级融合,直到最后的高精度图像,其总的运算量为nαN2lognN。
一般情况下,对于SAR成像处理,α=8的插值就能满足其精度要求,可以得到FBP算法和BP算法所用运算时间比为:
(4)
对于定值N,当n=e(e为自然对数)时,运算时间比可得到最大值。但由于n必须为整数,因此上式最大值出现在n=3处。当L=M=N时,BP成像算法耗时只与N有关,因此对于给定的N,当n=3时,FBP算法耗时最少、处理速度最快。通过分析,从上式还可知:当N≤128,n=2时,BP算法比FBP算法快;当N≤128,n=2时,FBP算法比BP算法快,且N越大,FBP算法相对于BP算法的速度就越快。
3 仿真分析
先采用点目标成像处理来验证BP和FBP成像算法,表1为点目标仿真模型参数。另外,FBP级数n=2,成像区域像素网格间隔为0.2 m×0.2 m,M=N=4 096。
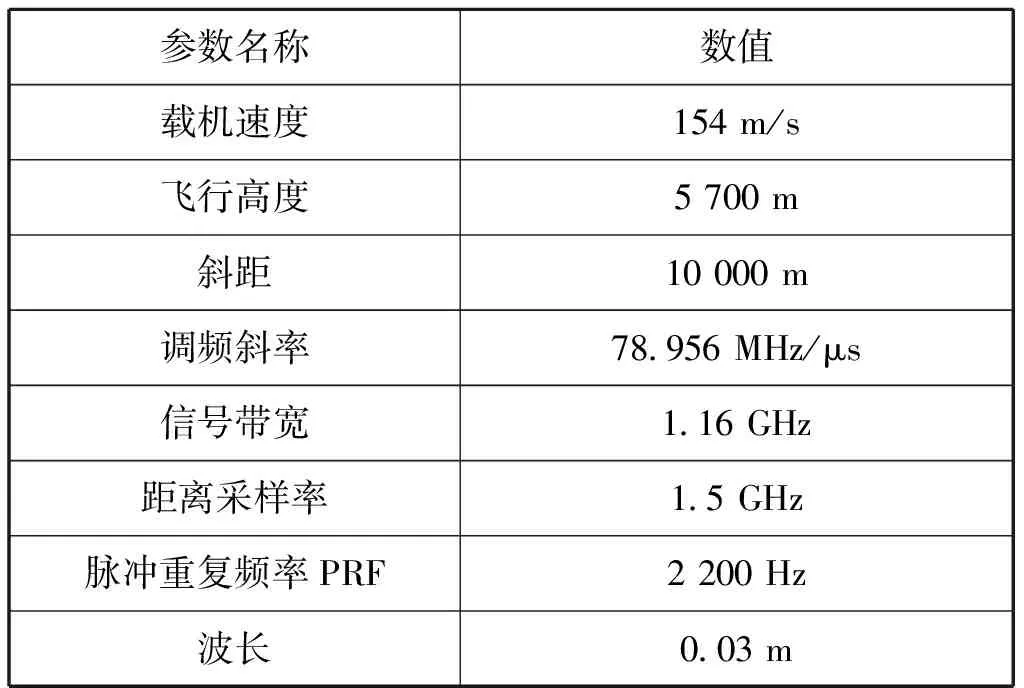
表1 聚束SAR仿真参数
通过BP算法和FBP算法处理的点目标仿真结果(图4和图5)可以看出,点目标距离向和方位向都具有较好的成像效果,初步验证2种算法的可行性。
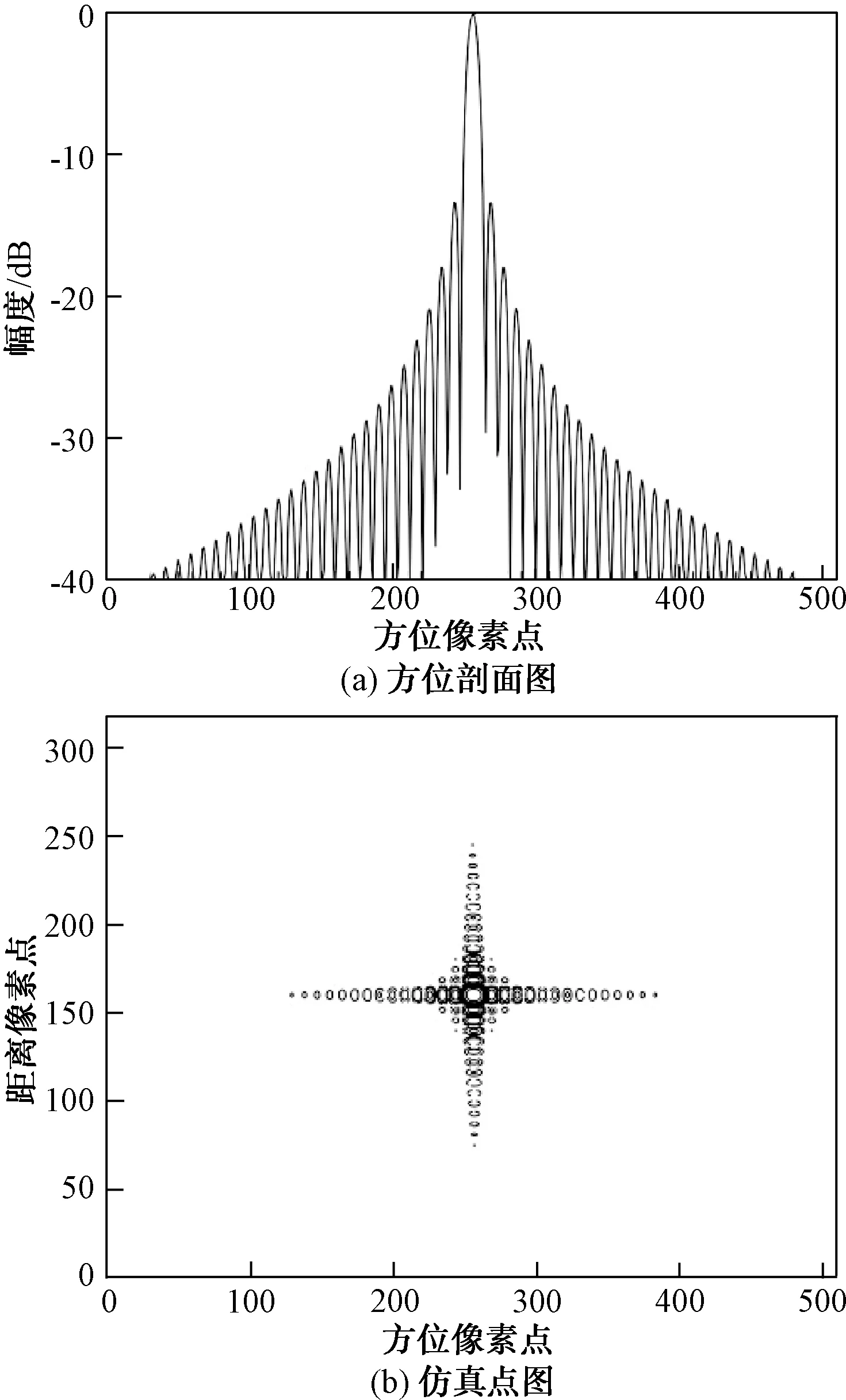
图4 BP算法仿真点图
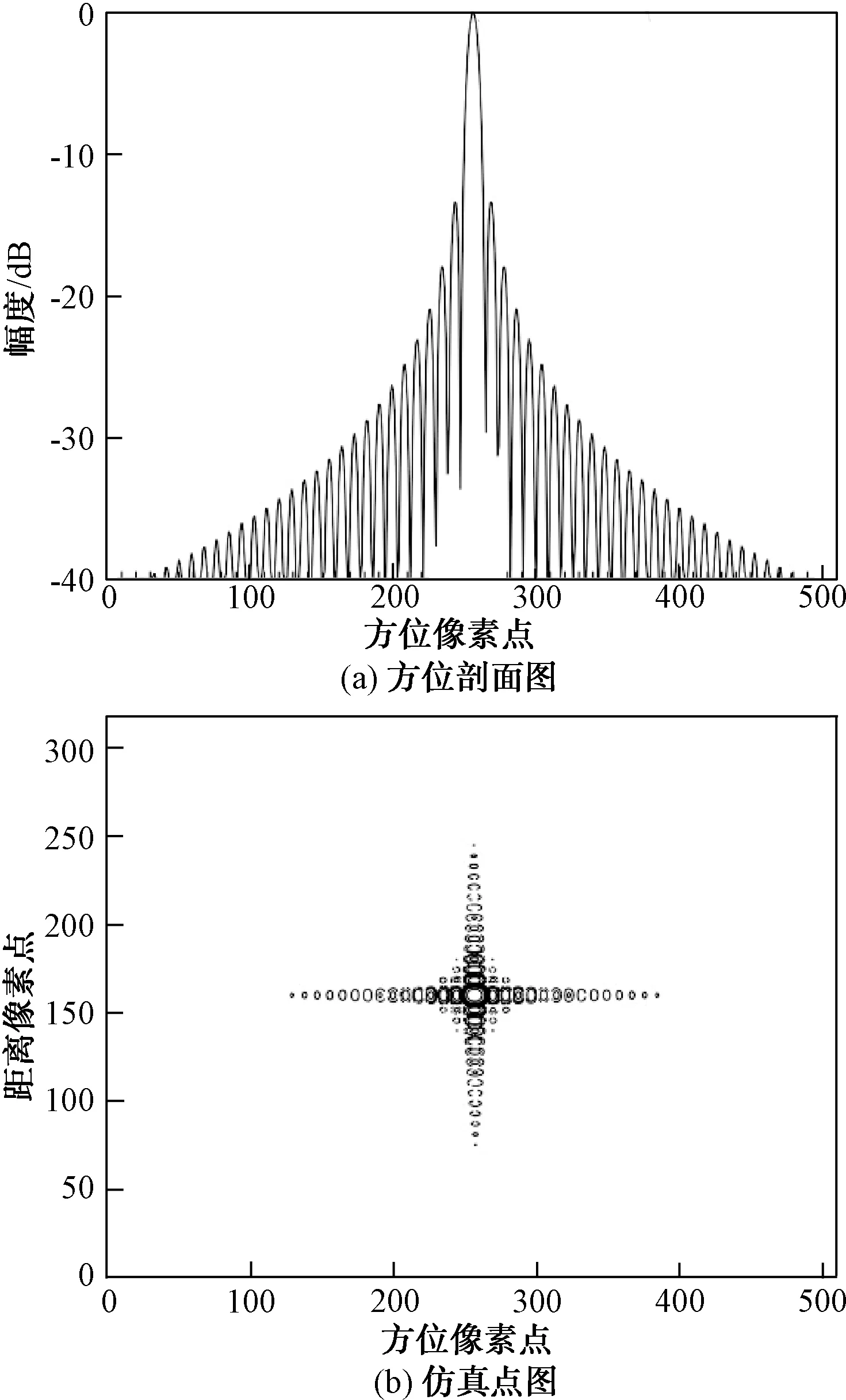
图5 FBP算法仿真点图
另外,分别采用BP算法和FBP算法对同一实测数据进行成像处理。成像大小为4 096×4 096,由图6可以看出 FBP成像效果相比于BP成像略差。

图6 BP和FBP实测数据成像
该实验采用同一硬件处理平台,其中BP耗时4 831 s,FBP算法耗时1 095 s,FBP比BP算法处理速度约快5倍。FBP算法虽然运算量减小,但是实测SAR图像清晰度相较于BP算法略差,说明
FBP算法运算量的减小是基于降低SAR图像质量的。
4 结束语
本文通过仿真对比分析了2种算法的成像效率以及成像效果。BP算法能够实现高精度SAR成像,但是由于其计算量巨大,难以工程实时运用;而FBP算法,在保证时域算法精度基础上,通过减少计算量,为后续工程运用提供了理论基础。
