航母编队情报融合系统同步特性分析

李 尧，耿伯英

(1.海军指挥学院,江苏 南京 210016;2.海军工程大学，湖北 武汉 430033)

0 引 言

同步是指复杂网络中多个节点的行为在时间和空间上达到精确配合的状态[1]。航母编队情报融合系统作为典型的复杂网络，各类节点在不断完成自身活动的同时，向上级情报保障中心传输态势信息。编队情报保障过程的同步特性影响着各舰艇情报保障的协同能力、编队获取态势信息的质量和时间。

文献[2]～[3]基于作战指挥进程的观察调整决策行动(OODA)环循环特性，提出了系统作战的协同动力学模子，并给出了作战系统协同的同步判据。文献[4]以获取信息、决策、行动三方面作为状态变量，建立了作战单元动力学模型，通过离散粒子群算法寻找动态最优网络。上述文献模型主要分析了同质作战单元的同步问题，忽略了节点间异质性。

本文针对网络化航母编队谍报融会过程同步问题，根据编队内部各舰艇及其部属传感器谍报保障行动的周期循环特征，定义各编组为动力学振子，基于耦合相位振子的Kuramoto模子，构建网络化航母编队情报融合同步描述模型，经由过程序参量和同步稳定时间对情报融合同步能力进行了理论和数值剖析，并讨论了4类因素对同步能力的影响。

1 编队情报融合动力学模型

航母编队情报保障过程主要包括情报侦察和情报处理[5]。情报侦察依托各种传感器，如舰载预警机、舰载雷达、电子侦察卫星等；情报处理依靠每艘舰艇上布设的作战情报中心以及旗舰的编队指挥中心。各种传感器将探测到的情报传输至本舰情报中心，进行融合处理后上报至编队指挥中心。图1为典型的航母编队情报融合网络，其中F表示旗舰指挥中心，f表示舰艇作战情报中心，s表示下属传感器，舰艇间虚线表示可能存在的信息共享。

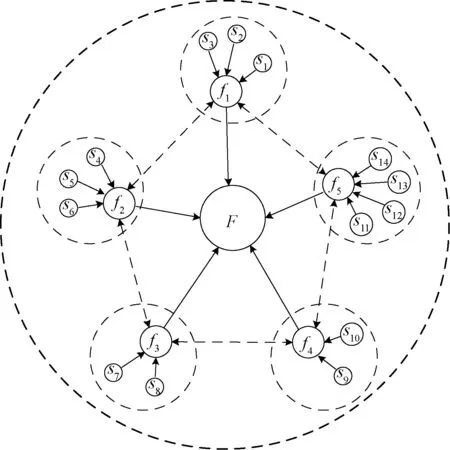
图1 航母编队情报融合网络示意图

将每艘舰艇及其下属传感器视为1个编组，单个编组的侦察、判断、融合、上报过程具有类似于OODA环的周期循环特性[6]，如图2所示。将单个编组视为动力学振子，可以用Kuramoto模子描述编组的循环特征，如图3所示。

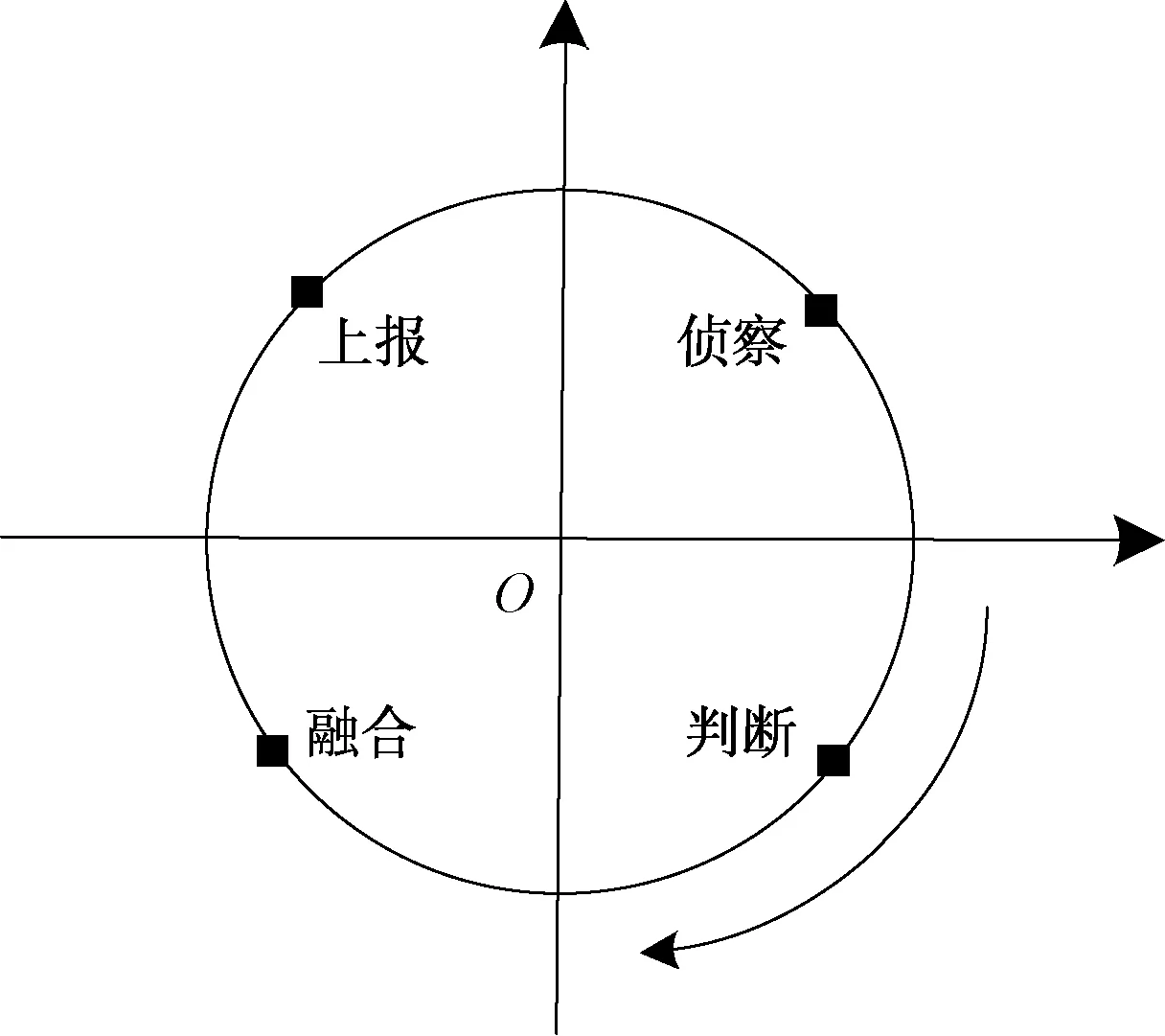
图2 情报保障周期循环过程

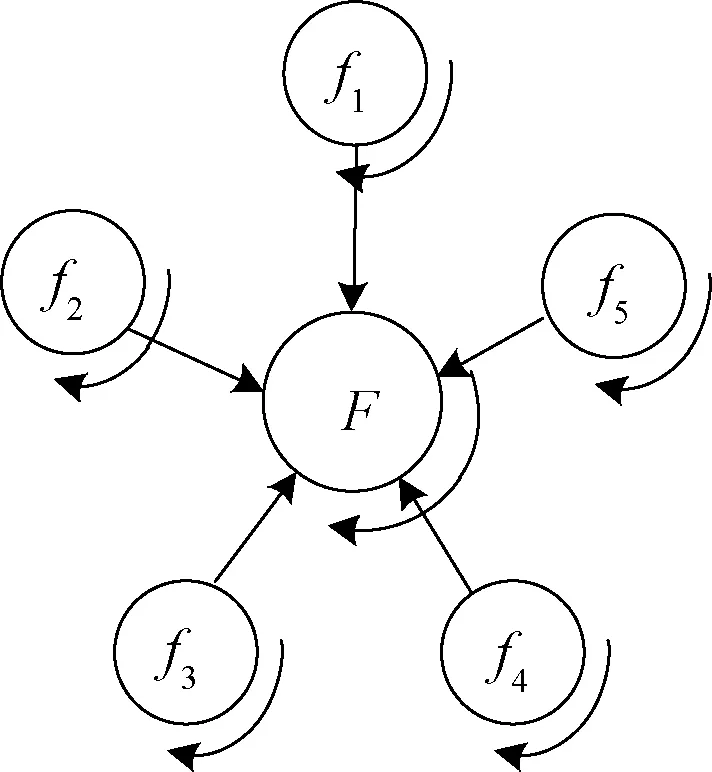
图3 编组振子示意图

考虑n个具有逻辑连接关系的编组振子和中心振子构成系统的集体动力学，单个振子的动力学表达式为：

(1)

式中：ωi表示振子i在独立完成情报保障过程中，完成侦察、判断、融合、上报循环的自然频率；θi指振子i的相位，且θi∈[0,2π)，表示振子i在循环过程中所处阶段，可假设θi∈[0,π/2)时，振子处于侦察阶段；θi∈[π/2,π)时，振子处于判断阶段；θi∈[π,3π/2)时，振子处于融合阶段；θi∈[3π/2,2π)时，振子处于上报阶段；Kij为振子i与振子j之间的耦合强度，即两艘舰艇之间信息交互水平，若两艘舰艇间的信息共享水平越高，Kij越大；若两艘舰艇之间无信息交互，则取Kij=0。

2 情报融合同步能力度量

情报融合同步是对各舰艇情报保障活动在时间和空间上达到精确配合状态的描述。为了对航母编队同步能力进行数值分析，从序参量和同步稳定时间两方面进行度量。

公式(1)表达的是均匀耦合的情况，即Kij=K/(n+1)>0。该式还可以写成如下形式：

(2)

显然各振子情报保障活动的周期并不相同，但是在完成情报上报融合过程时，各节点必须趋同，才能保证战斗节奏一致。根据Kuramoto模型[7-8]，用2个参数来衡量其同步本领：一是序参量，二是到达稳定同步所需时间。

由中心振子和n个编组振子构成的系统，其序参量由下式计算：

(3)

r(t)越大，表示t时刻各编组振子相位越一致，所处侦察、判断、融合、上报过程越接近，同步效果越好；反之亦反。当r(t)=1时，各振子相位达到最大程度同步，效果最佳。

系统经过一定时间后可能趋于稳定，也可能发散，且r(t)随时间动态变化。为权衡系统的稳定状态，考察系统的序参量r(t)，如果∀Tε>0，当t>Tε时，都能够找到一个较小的常数ε，使得对于任意的Δt>0，都有|r(t+Δt)-r(t)|≤ε，则认为该系统在时间Tε之后达到稳定的同步状态。并且，使系统达到稳定同步所需的最小时间Tmin称为同步稳定时间。

因此，系统中各节点达到稳定的时间越短，稳定后序参量越大，则各编组振子同步能力越好，用下式量化计算：

M=r·βTmin

(4)

式中：M为编队同步能力；r为达到稳定状态后系统序参量的均值；β∈(0,1)，为关于系统稳定时间的影响系数，系统对同步时间要求越高，影响系数越大，则β取值越小，反之β取值越大。

下面考察振子不能达到稳定状态时同步能力的度量。根据文献[9]，此时分为2种情况：一是振子以固定的振荡周期作循环运动，此时各振子可以相互配合完成任务；二是振子无固定收敛周期而发散，此时无法保证任务的完成。根据以上2种情况，建立模型计算系统的同步能力：

(5)

式中：r为振子以固定周期振荡运动时序参量的均值；rmax、rmin分别为振荡运动中序参量的最大值和最小值；T是最小振荡周期；γ为振荡周期影响系数，γ∈(0,1)，当系统对振荡周期的要求越严格时，影响系数越大，即γ取值越小。

3 仿真分析

假设某航母编队由旗舰及其余5艘舰艇组成，舰艇自身布设作战情报中心，下属多个传感器。将每艘舰艇及其下属传感器视为编组振子，旗舰视为中心振子。根据不同的作战任务，舰艇间会形成不同程度的信息共享关系，图4描述了3种不同作战任务下航母编队的编成简化结构。

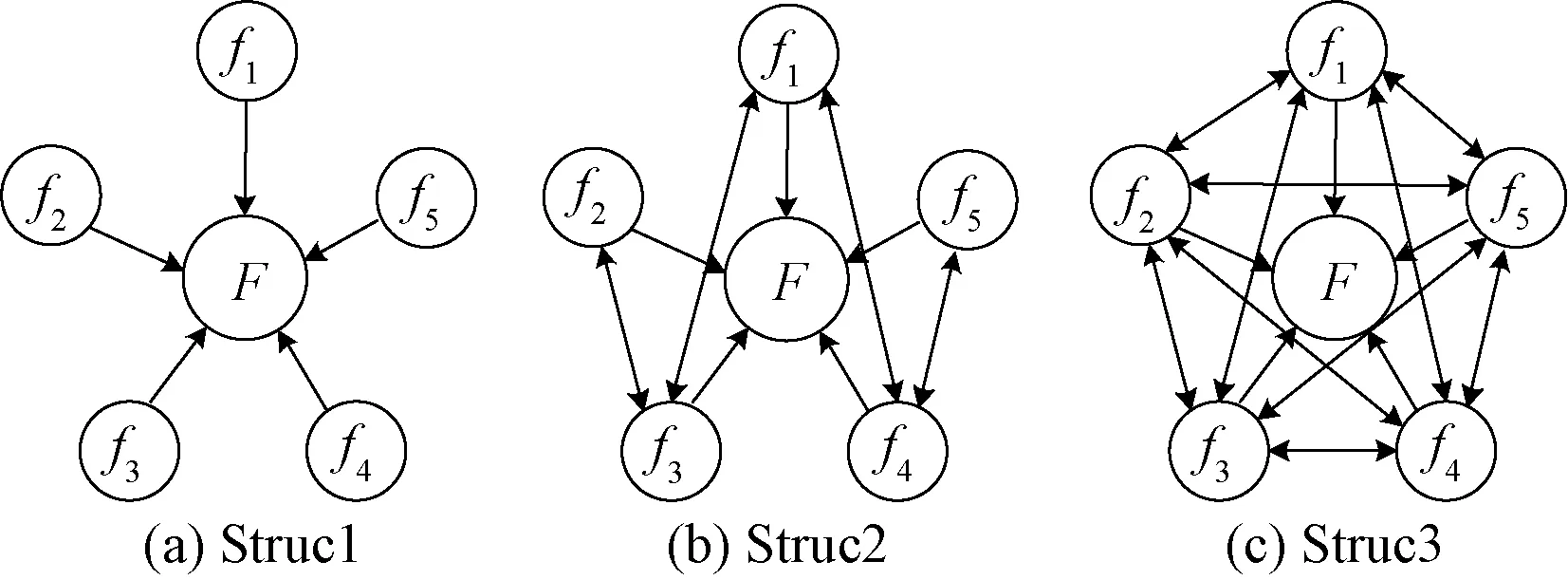
图4 不同作战任务下航母编队结构图

由式(1)可知，影响编组间动力学同步的因素包括编组间逻辑连接关系、编组间耦合强度、各编组的自然频率以及初始相位。仿真实验中，取参数β=0.9，γ=0.8，常数ε=0.01，仿真时长为10个单位时间。

3.1 逻辑连接关系的影响

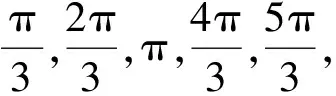
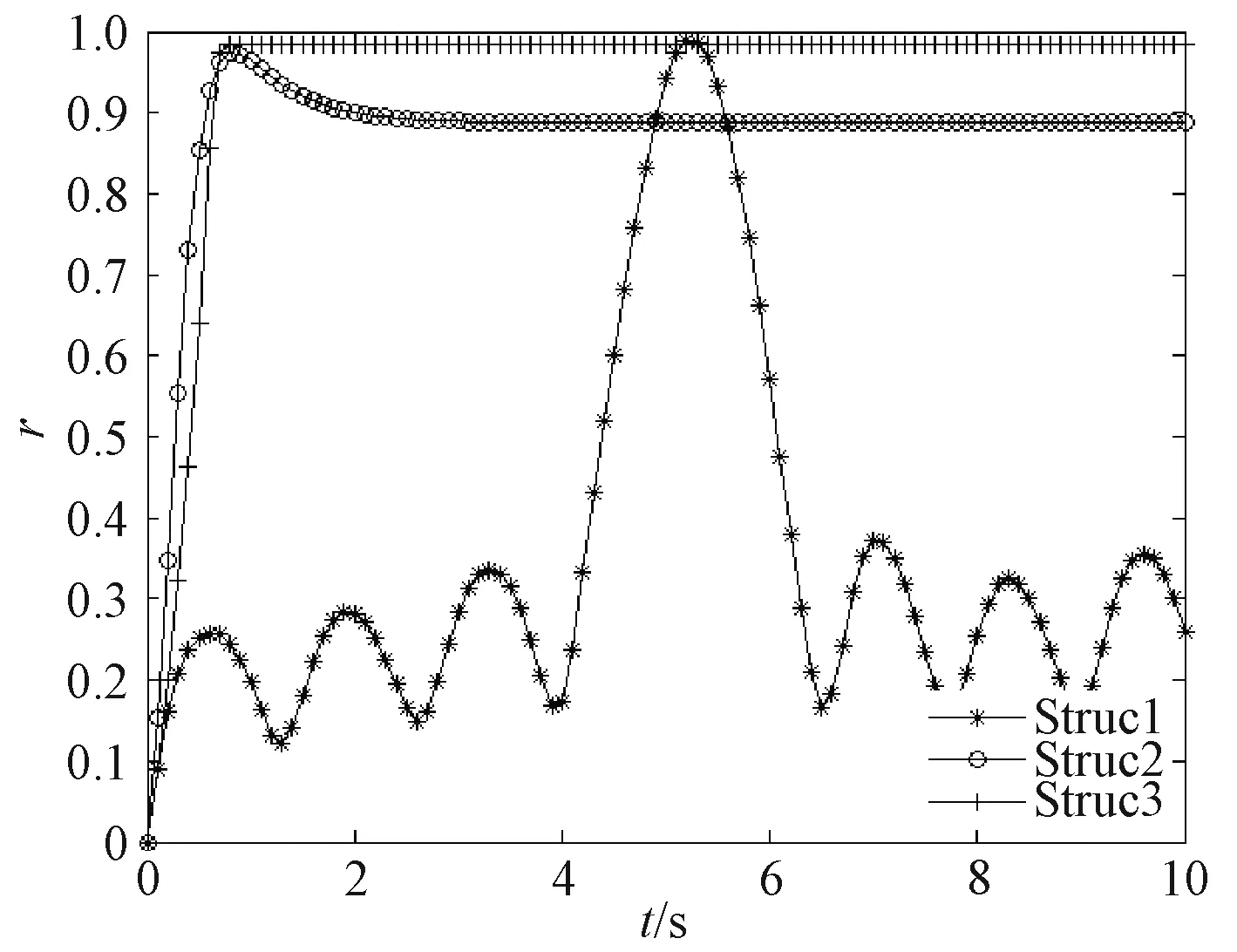
图5 3种结构下序参量随时间变化图

经计算，对于Struc1，r1=0.383 6，rmax1=0.988 8，rmin1=0.165 3，T=6.6单位时间；对于Strcu2，r2=0.888 2，Tε2=3.0单位时间；对于Strcu3，r3=0.984 8，Tε3=0.9单位时间。由此可得3种结构的同步能力：M1=0，M2=0.647 5，M3=0.895 7。

可以看出，Struc3最快达到同步，其次是Struc2，Struc1则无法达到同步。同时，Struc2和Struc3的序参量均小于1，即2种结构均无法达到完全同步，且Struc3的序参量大于Struc2，即Struc3的同步效果优于Struc2。

进一步分析可知，导致3种结构同步效果不同的原因在于逻辑连接关系不同。Struc1中编组间无耦合作用，Struc2中编组间存在弱耦合作用，Struc3则形成全连通网络，耦合程度最大。因此，增强航母编队舰艇之间的信息共享程度能够促进编队对信息融合过程的同步。

3.2 耦合强度的影响

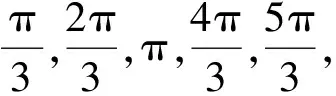
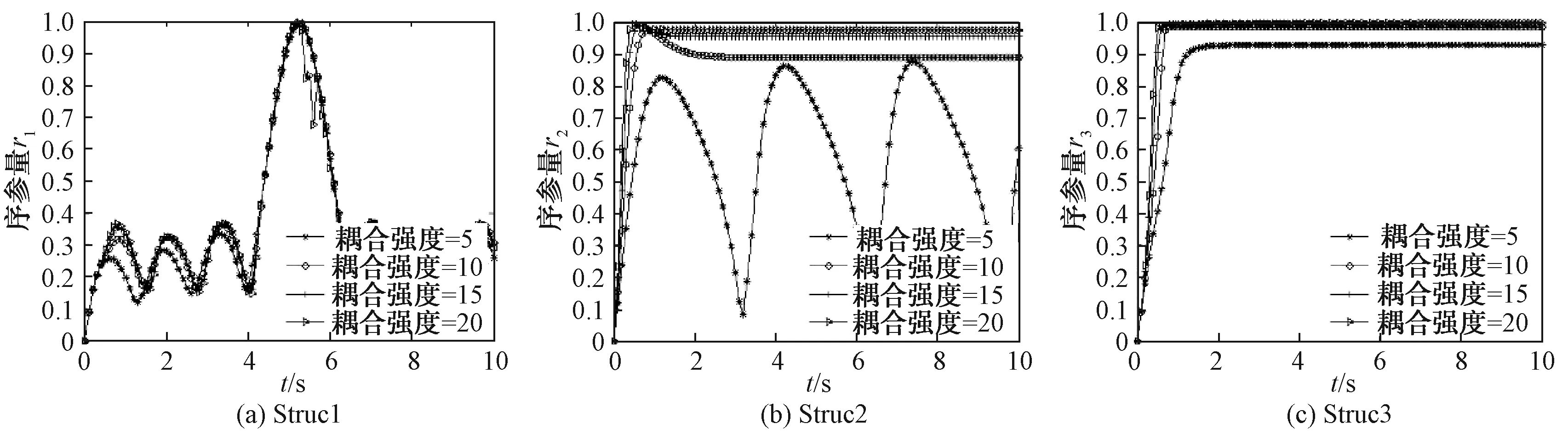
图6 耦合强度对序参量的影响图

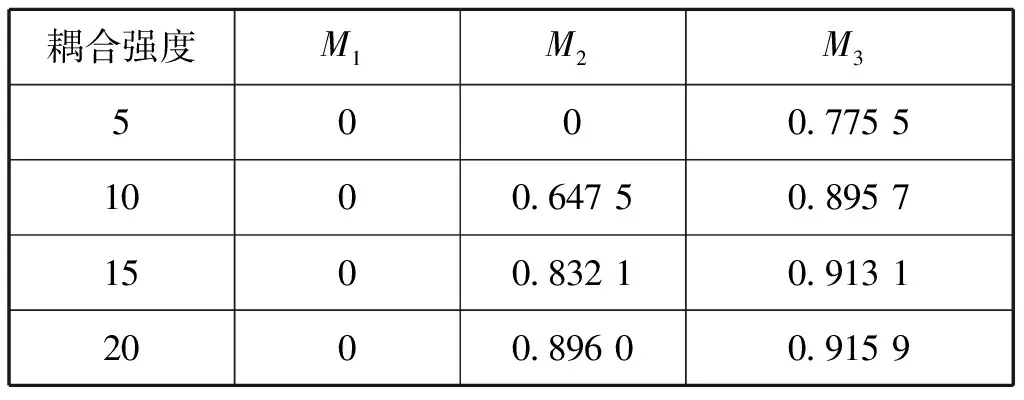
耦合强度M1M2M35000.775 51000.647 50.895 71500.832 10.913 12000.896 00.915 9

编组间耦合强度影响着航母编队情报融合的同步效果。从图6可以看出，对于编组间无逻辑连接关系的Struc1，无论耦合强度如何改变，其同步能力均为0；对于编组间存在逻辑连接关系的Struc2和Struc3，耦合强度的增大对同步效果起促进作用。同时注意到图3(b)中，编组间耦合强度Kij=5时，该结构的同步能力为0，表明即使编队舰艇间存在信息共享，若共享程度极小，编队的情报融合过程依然无法达到同步。

3.3 自然频率的影响

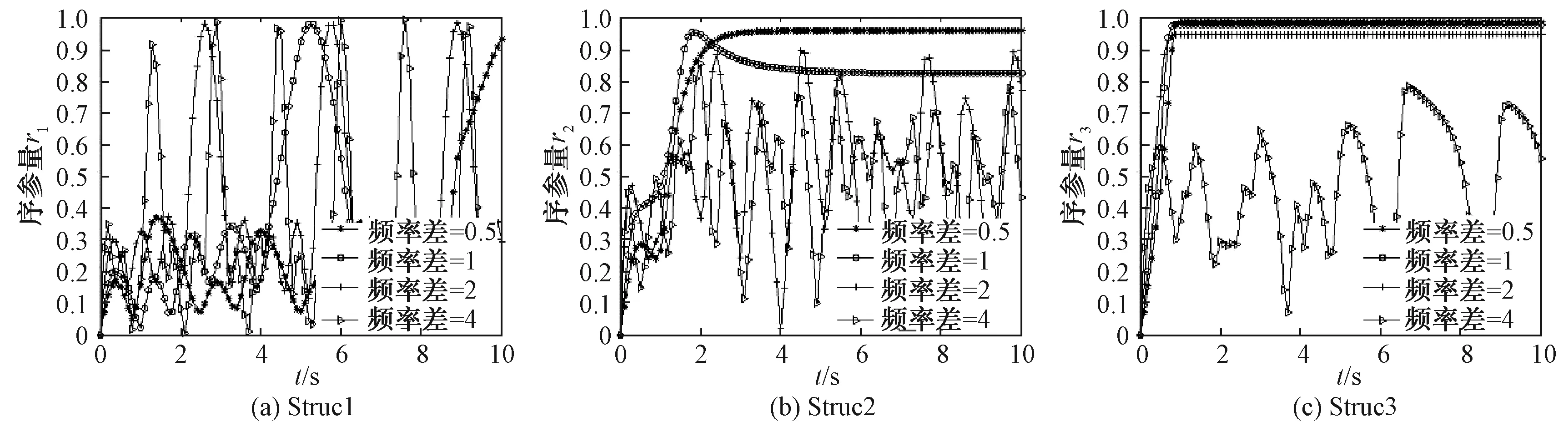
图7 自然频率对序参量的影响图

计算得到编组自然频率取值不同的情况下3种结构的同步效果，如表2所示。

显然，编组间自然频率差越小，编队的情报融合过程更容易达到同步状态，且同步能力越好。

3.4 初始相位的影响

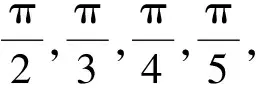
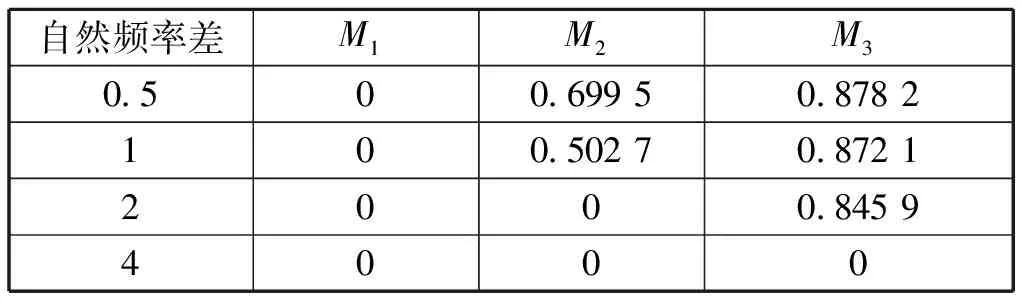
表2 自然频率对系统同步影响结果

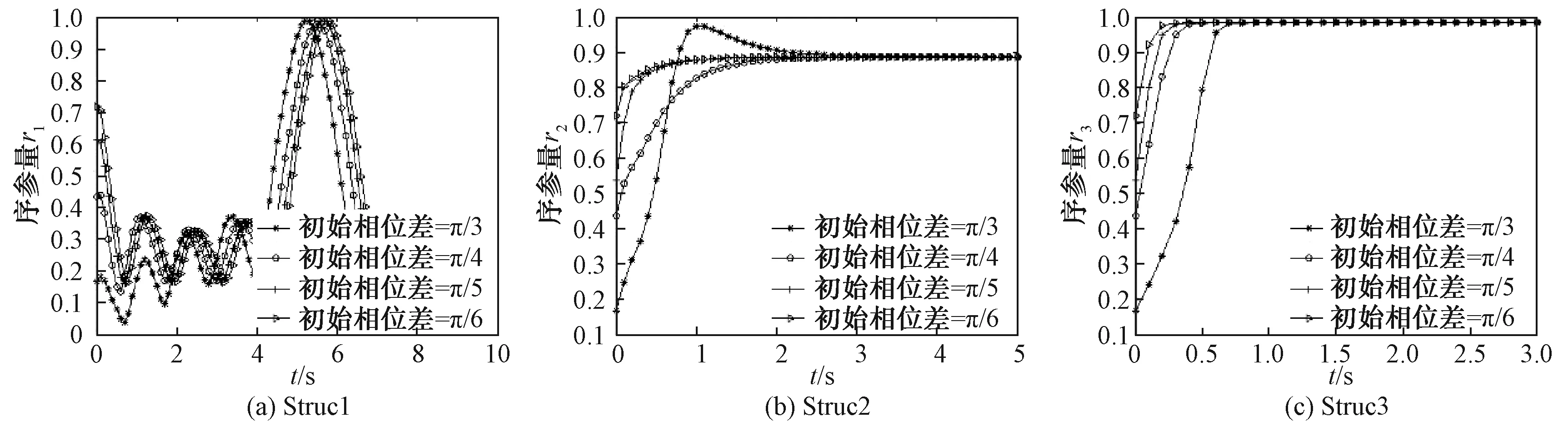
图8 初始相位对序参量的影响图

从图8可以看出，对于编组间无逻辑连接关系的Struc1，改变初始相位差无法改变其不同步状态；对于Struc2和Struc3，减小编组间初始相位差，能够使得编队信息融合过程更快达到同步。应当注意的是，改变编组间初始相位差并不影响序参量的稳定值。

4 结束语

航母编队情报保障能力直接关系着编队的作战效能。本文在分析航母编队情报保障过程的基础上，基于动力学振子的Kuramoto模型，从序参量和同步稳定时间两方面研究了影响编队情报融合同步特性的因素。仿真实验表明，编队舰艇间充分、广泛的信息共享能够减小完成同步的时间，并达到更稳定的同步状态；各舰艇编组完成侦察、判断、融合、上报循环的频率差、初始相位差越小，编队的同步能力越高。

本文在研究中存在不足之处。注意到虽然全连通状态的航母编队结构能够使同步效果最佳，但如第2种结构下非全连通的航母编队同样能够达到较好的同步效果。因此，在考虑舰艇情报中心处理能力以及通信代价的前提下，如何选取编队结构以获取最大的同步效益，是本文下一步的研究方向。