MIMO-OFDM系统基于指数平滑的 改进信道估计算法

苏 生，李 琳

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

MIMO-OFDM是一种能够有效满足4G/5G无线移动通信需求的传输方案[1]。MIMO技术和OFDM技术的结合能够在避免频率选择性衰落的同时，实现高速率信号传输和大信道容量[2]。然而，在宽带无线移动通信系统中，无线信道具有频率选择性衰落和时变特性，在MIMO-OFDM系统中需要对信道做动态的估计。因此，对于MIMO-OFDM系统信道估计的研究吸引了广大学者的关注[3]。

信道估计方法主要有盲信道估计、半盲信道估计和基于训练序列的非盲信道估计三个大类，由于盲信道估计和半盲信道估计都存在着运算复杂度高、算法收敛速度慢的不足，专家学者对于非盲信道估计有着更为广泛的研究[4]。根据最小二乘准则，文献[5]提出了MIMO-OFDM系统中的LS信道估计算法，LS信道估计算法具有运算复杂度低、实现简单的优势，然而信道估计过程中LS算法忽略了无线环境中的噪声，因此在低信噪比环境下，LS信道估计算法的估计精度低。为了解决这一不足，文献[6]提出了最小均方误差(MMSE)信道估计算法，充分考虑了无线环境中的噪声和信道的自相关性，有效抑制了噪声，提升了信道估计的精度。然而，随着相关矩阵维度的增加，MMSE估计算法的运算复杂度剧烈增加，同时，由于需要获得无线信道的统计特性，MMSE估计算法在实际中运用的较少。为了同时满足高估计精度和低运算复杂度，研究人员提出了一些改进LS信道估计算法的思路[7-9]。文献[9]给出了基于离散傅里叶变换(DFT)的信道估计算法，通过将信道冲击响应(CIR)在最大时延长度外的部分设为零，DFT信道估计算法能有效抑制加性高斯白噪声，并且DFT估计算法的运算复杂度低。然而，DFT估计算法中需要提前获取信道的最大时延长度，在时变信道环境中不便于实现。为了解决上述信道估计算法中的问题，本文将指数平滑算法和LS信道估计算法相结合，创新提出MIMO-OFDM系统中改进的LS信道估计算法。对于时变信道，相邻时间的信道冲击响应变化是有规律可循的，根据这一特性，本文提出的改进算法利用过去时刻预测的信道冲击响应值和预测误差来修正当前时刻的信道冲击响应估计值，通过迭代运算，可以获取所有时刻预测的信道冲击响应。同时，指数平滑算法具有等效低通滤波的特性，无线信道中的随机干扰能够被有效抑制。因此，与LS信道估计算法相比，本文提出的改进信道估计算法的精度得到提升，与DFT信道估计算法相比，最大时延长度不需要再获取，因而，LS估计算法和DFT估计算法中面临的问题得以解决。

1 系统模型

1.1 MIMO信道模型

本文基于抽头延迟线信道模型，建立了一般的MIMO信道模型[10]，表示如下：

(1)

式中：L为传输路径数；τl(t)为t时刻第l个路径的时延；δ(·)表示冲激响应函数；Al(t)为t时刻第l个传输路径的信道系数矩阵[11]，矩阵的组成如下：

(2)

因此，t时刻第i个发射天线到第j个接收天线之间的信道冲激响应可以表示如下：

(3)

信道建模时，一般考虑一个OFDM符号时间内信道冲激响应保持不变，OFDM符号之间信道冲激响应函数随时间变化，因此公式(1)可以简化为：

(4)

因此，公式(3)可表示为：

(5)

对于离散时间系统，hji(τ)可近似为一个向量[12]：

hji=[hji(1),hji(2),…,hji(L)]T

(6)

1.2 MIMO-OFDM系统模型

图1给出了本文采用的MIMO-OFDM基带传输模型，其中NT和NR分别表示发射天线数和接收天线数，初始比特流完成正交相移键控(QPSK)调制后生成原始符号，然后将串行符号做串并变换，接着对各并行符号做空时编码，分配到各个发射天线，各发射天线对符号做导频插入、快速傅里叶逆变换(IFFT)运算后生成OFDM符号，最后加入循环前缀，经各发射天线送入信道，接收端的传输流程与发送端对应，移除循环前缀后，接收的信号经过快速傅里叶变换(FFT)、信道估计、空时解码、并串变换、QPSK解调等步骤后，解算出初始比特流。其中，为消除信号多径传播引起的符号间干扰，循环前缀的长度Lg要大于多径信道的最大时延L[13]。

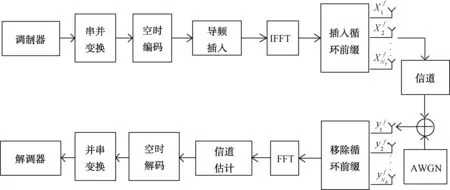
图1 MIMO-OFDM系统

以第j个接收天线为例，移除了循环前缀的时域接收信号表示为：

(7)

(8)

通过对时域接收信号做FFT变换可以得到接收信号的频域表达形式，表示为：

(9)

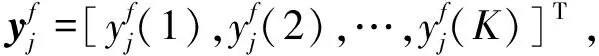
2 MIMO-OFDM系统信道估计

本节简要介绍了经典LS信道估计算法，并详细推导了基于指数平滑的改进信道估计算法。2种算法在推导时，均认为OFDM符号之间的信道冲激响应变化缓慢，导频插入方式采用梳状导频，且不同天线导频的位置相互正交[15]。

2.1 经典LS信道估计算法

根据最小二乘准则，LS信道估计利用插入的导频信号和对应的接收信号来估计信道值。结合公式(9)，导频插入位置对应的频域接收信号为：

(10)

式中：上标P表示导频所在位置。

为便于推导，将公式(10)中来自所有发射天线的导频信号为：

(11)

式中：Qm(n)表示来自第m个发射天线的第n个导频信号；p为导频间隔。

将所有的导频信号排列为对角矩阵Q，表示为：

Q=diag(Q1(1),Q2(1),…,QNT(1),Q1(2),Q2(2),…,QNT(2),…,Q1(M),Q2(M),…,QNT(M))

(12)

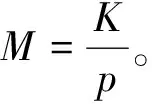
根据Q的表达式，所有发射天线到第j个接收天线的信道频率响应可以表示为：

(13)

因此，公式(10)可以转换为如下形式：

(14)

基于公式(14)，信道状态系数的LS信道估计为：

(15)

其中：

(16)

2.2 改进信道估计算法

2.2.1 指数平滑算法

指数平滑[17]是一种分析时间序列变化趋势且运算复杂度低的算法，它能有效抑制随机因素带来的干扰，揭露时间序列隐藏的变化规律。对时间序列，指数平滑算法通过过去时刻的序列变化趋势来预测当前时刻的序列值，具体为：为了减少估计误差，需要通过迭代运算，根据过去时刻的预测值和预测误差，来修正当前时刻的估计值。由于预测过程是规律的，因此由随机因素产生的干扰能被有效抑制。

指数平滑算法的递归公式表示为[18]：

(17)

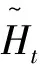
对公式(17)做迭代运算，可以得到：

(18)

公式(17)也可变换为：

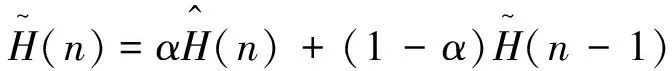
(19)

公式(19)实际为数字滤波器的表达式，其系统函数为：

(20)

其中，滤波的频率响应为：

(21)

幅频响应为：

(22)

由于α在0到1之间取值，该数字滤波器本质上为低通滤波器[19]。由于随机干扰分布于信号的各个频段，因此利用指数平滑算法可以滤除位于中高频的干扰，从而提升估计的精度。对于不同的α，图2给出了滤波器的滤波效果，可以看出，平滑系数越小，低通滤波的效果越明显。

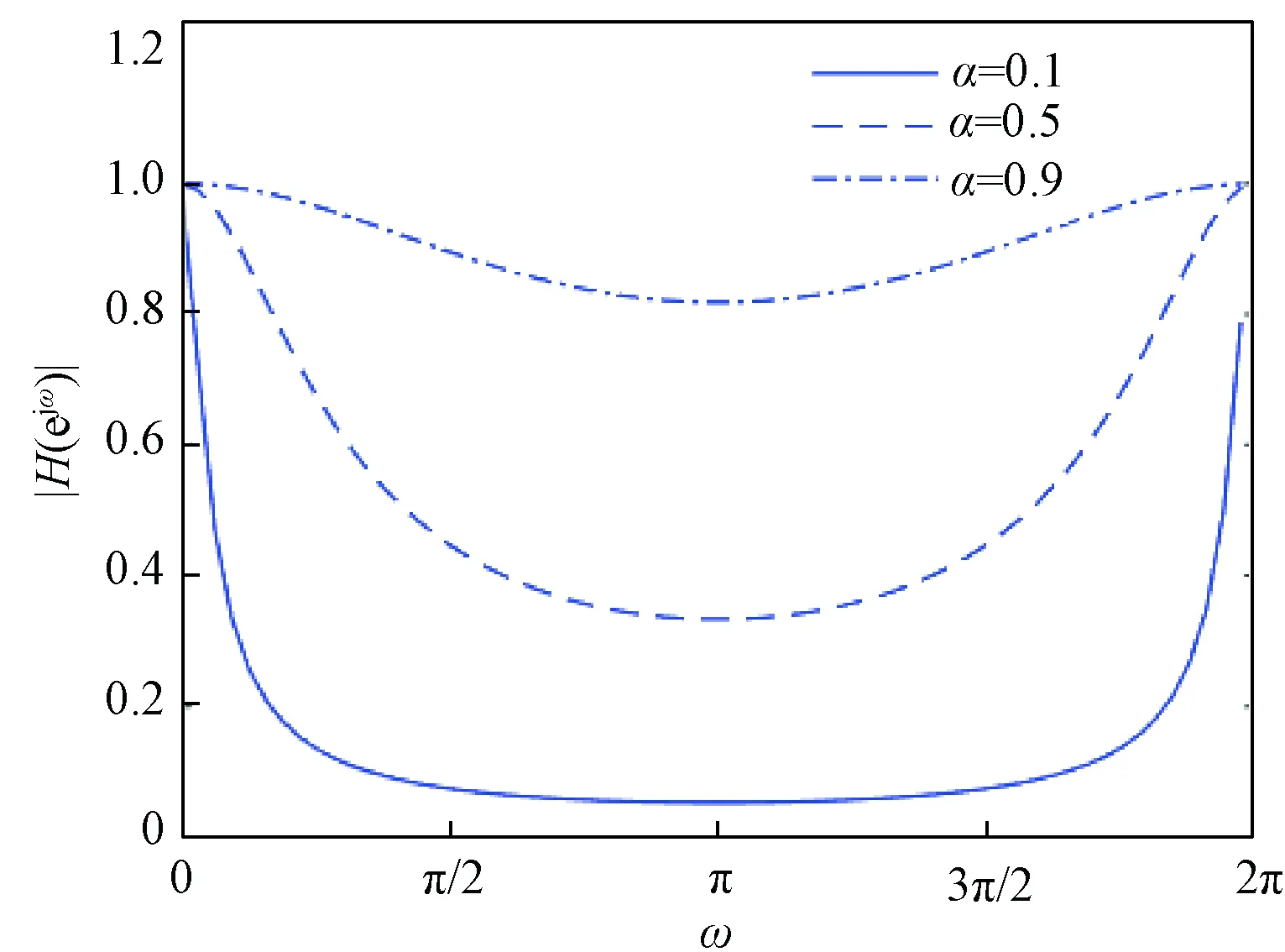
图2 指数平滑算法幅频特性

2.2.2 基于指数平滑算法的改进LS信道估计算法

本小节将通过经典LS信道估计算法推导得到基于指数平滑的改进信道估计算法。根据文献[19]，信道冲激响应在OFDM符号之间变化缓慢时，一个OFDM符号内的信道冲激响应可以看做一个低频信号，同时，加性高斯白噪声分布于所有频率范围[20]。因此，具有等效低通滤波效果的指数平滑算法可以运用到LS信道估计算法中，抑制噪声，提升信道的估计精度。

基于指数平滑的LS信道估计算法流程如图3所示，首先要执行离散傅里叶逆变换(IDFT)来获取LS信道估计算法在时域的信道冲激响应估计值，此估计值即作为指数平滑的观察值；然后通过指数平滑算法预测出每一时刻的信道冲激响应；最后再将指数平滑后的信道冲激响应做离散傅里叶变换(DFT)得到频域的信道估计值。

用公式表示为：

(23)

(24)

(25)

3 仿真结果

本小节基于上述的分析，对改进信道估计算法做了仿真，并与LS、DFT、最小均方误差(MMSE)信道估计算法的性能做了比较分析。仿真参数如表1所示，其中导频的为梳状导频，不同天线上的导频位置相互正交，同时，信道冲激响应在OFDM符号之间变化。

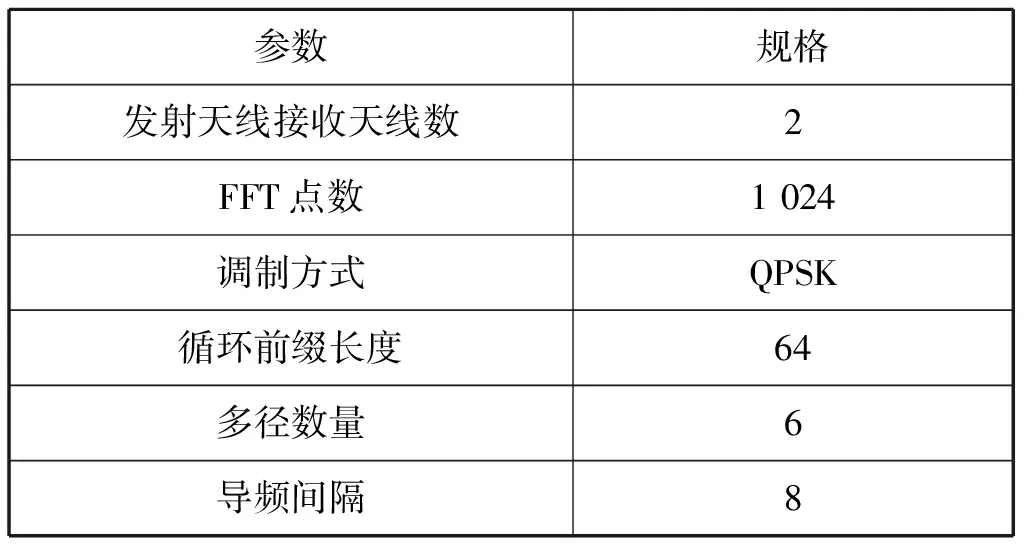
表1 仿真参数

图4给出了改进信道估计算法在不同信噪比和平滑系数下的估计性能。可以看出，在低信噪比环境中，随着平滑系数的减小，估计误差随之减小；然而，在高信噪比环境中，随着平滑系数的减小，估计误差反而增加。因此本文选取了低、中、高3种信噪比环境，通过仿真找出了对应最佳的指数平滑系数，3种信噪比对应为0 dB、14 dB、28 dB，与之对应的最佳平滑系数分别为0.1、0.3、0.4。

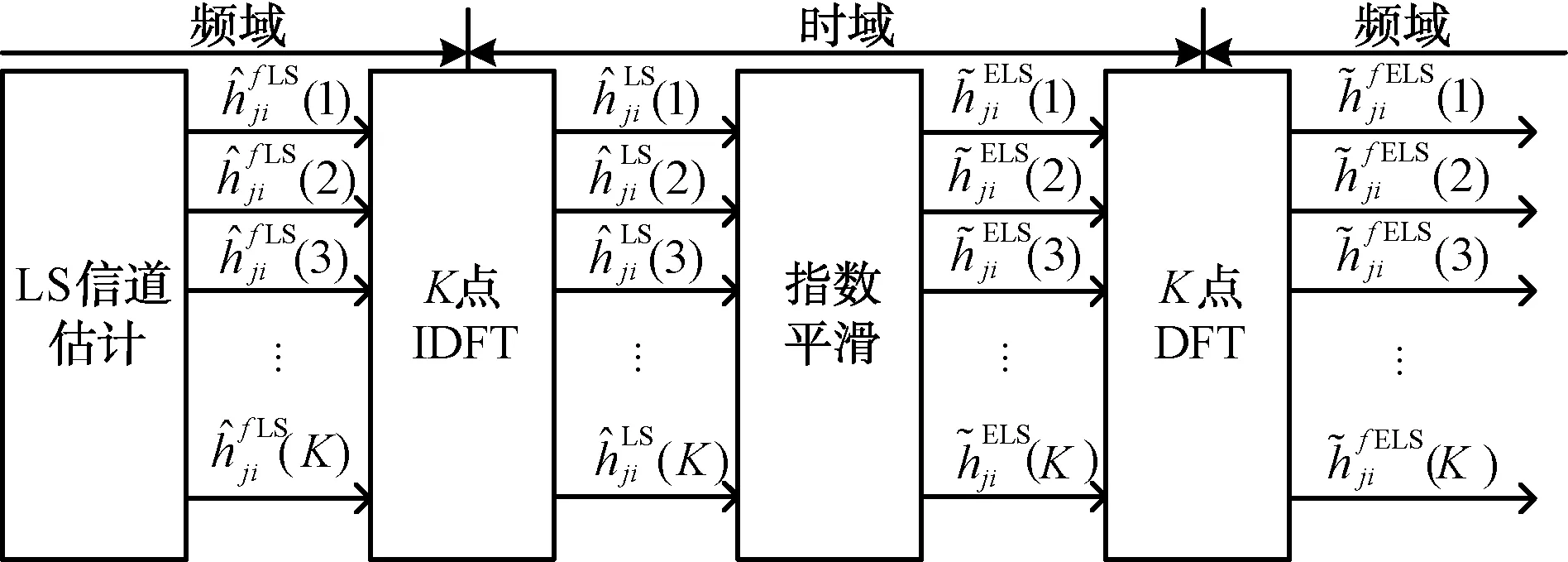
图3 指数平滑算法流程图

图5给出了各信道估计算法的估计误差，与LS估计算法相比，当平滑系数为0.3和0.4时，基于指数平滑的改进估计算法的估计误差要小于经典LS信道估计算法。指数平滑算法具有等效低通滤波特性，能够滤除部分LS信道估计中引入的噪声。同时，平滑系数为0.4时，改进算法的估计精度接近DFT信道估计算法，同时还避免了DFT信道估计算法中需要获取最大时延长度的问题。此外，在高信噪比环境下，平滑系数越小，估计误差越大，这是由于在高信噪比环境中，接收信号中有用信号占主要部分，平滑系数越小，低通滤波性能越强，此时指数平滑算法滤除了部分有用信号，从而导致了估计误差的增加。因此，对于所有的信噪比环境，既要滤除信号中的噪声，也需要保护有用信号，本文选取了0.4作为最优平滑系数。最后，观察MMSE算法的估计效果可以看出，MMSE信道估计算法的估计精度最高，但是运算复杂度也最高。

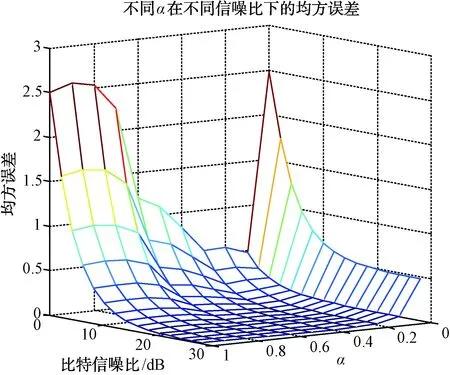
图4 基于指数平滑的改进LS算法在不同α和 信噪比下的均方误差曲线图

图5 基于指数平滑的改进LS算法均方误差曲线图

图6 基于指数平滑的改进LS算法误比特率曲线图

图6给出了LS、DFT、MMSE以及选取了最优系数指数平滑算法的估计误比特率性能，与前述分析一致，指数平滑算法改善了经典LS信道估计算法的估计精度，降低了误比特率，同时与DFT估计算法相比，指数平滑算法估计精度与其接近，且避免了获取最大时延长度的问题。

因此，可以看出指数平滑算法是一种有效提升LS信道估计算法的方案，同时，与广泛使用的DFT信道估计算法相比，指数平滑算法避免了最大时延长度的问题，与MMSE信道估计算法相比，尽管指数平滑算法精度不如MMSE算法，但是指数平滑算法运算复杂度低，易于实现。

4 结束语

指数平滑算法能够揭露隐藏在时间序列背后的一般变化规律，抑制时间序列中的随机干扰。因此，在时变信道中，由于加性高斯白噪声，经典LS信道估计算法精度低，可以采用本文提出的方法来改进估计精度，减少估计误差。

指数平滑的效果随着不同的平滑系数发生变化，在低信噪比环境中，平滑系数越小，估计性能越好；而在高信噪比环境中，平滑系数越小，估计结果越差。因此，需要对所有信噪比环境选择一个最优的平滑系数。

本文建立了多径信道传输模型，并通过估计均方误差和误比特率验证了指数平滑算法带来的估计算法改善。仿真结果表明，指数平滑算法有效改善了经典LS信道估计算法的估计精度,同时与DFT信道估计算法相比，一个显著的优势是指数平滑算法无需获取多径信道的最大时延长度，且指数平滑算法能够将LS估计算法的估计精度改善到与DFT估计算法相近。最后，与MMSE信道估计算法相比，指数平滑算法运算复杂度低，易于实现。