电子战无人机干扰固定站雷达的时间规划研究

张新宇，张友兵，李仙茂，甘厚吉

(海军工程大学，湖北 武汉 430033)

0 引 言

现代化战争中，战场环境复杂多变，威胁来源多，相对于传统的干扰方式，无人机干扰具有明显的优势，其扮演的角色也越来越重要，将是决定未来战争胜利的关键因素之一[1]。无人机的生存能力强，红外特征小，雷达截面积(RCS)很小，自身隐蔽性好，反应快，操作灵活。由于无人机可以采取“抵近式”干扰，无人机上的雷达干扰机能以较小的干扰功率达到较好的干扰效果，同时干扰机接收到的雷达信号功率强，灵敏度要求不高，这些都简化了对干扰设备的要求。无人机可以无人值守自主飞行，对重点目标持续干扰时，终端用户只需要编程来完成任务，然后分批次轮流执行任务，做到不间断对重点目标进行干扰。无人机主要执行的是“抵近式”干扰任务，远离己方的其他电子设备，不对己方的电子设备正常工作产生干扰。当无人机用于干扰岸基固定站雷达时，可掩护作战飞机突防，无人机与作战飞机的配合中涉及到起飞时间、干扰时间和撤回时间等问题。因此，有必要深入研究满足战场限制条件下的无人机运用的时间规划问题[2]。

1 无人机起飞时间规划

无人机干扰的目的是掩护已方作战机群成功突防对方的警戒雷达[2]，假设已方作战飞机距离对方警戒雷达的水平距离为Dt，飞行高度为Ht，无人机距离对方警戒雷达为Dj，突防飞机在干扰无人机方向上的暴露距离为R0，无人机、警戒雷达、作战机群在同一直线上，作战场景如图1所示。

图1 作战场景平面示意图突防飞机的飞行速度(匀速)

作战飞机速度v1=800 km/h，飞行高度Ht=6 000 m，RCS值σ=40 m2，无人机飞行速度v2=150 km/h，飞行高度Hj=600 m，可回收航程(单向航程)S=200 km，警戒雷达的天线增益为Gt，雷达发射机输出功率为Pt，被探测目标的雷达散射截面积为σ，雷达的工作波长λ=0.3 m。

雷达的作用距离公式[3]为：

(1)

式中：Prmin为雷达的最小可检测信号功率，即雷达接收机的灵敏度，在实际应用中常常用最小输出信号噪声功率比(S/N)min来表示，即：

(2)

式中：k为玻尔兹曼常数；T为以绝对温度表示的接收机噪声温度；Δf为接收机的通频带；F为噪声系数。

对于岸基警戒雷达，其接收机灵敏度[4]Prmin=-90 dBm。由式(1)可以得到警戒距离Rmax与作战机群RCS的关系，如图2所示。

图2 警戒雷达探测距离与目标RCS值的关系

由图2可知，当突防机群的RCS值增大时，警戒雷达的探测距离不断增加，增长率逐渐降低。当突防机群的RCS值为40 m2时，警戒雷达可探测的距离Rmax约为380 km。由雷达方程计算可知无人机的安全距离约为4 km，考虑到光电装备对无人机的观察能力，将无人机布置到距警戒雷达20 km的距离上实施掩护，要求干扰无人机在突防机群到达警戒距离前2 min到达指定干扰距离，对敌警戒雷达实施干扰。假设突防机群起飞时间为T0=0时刻，干扰无人机从t时刻起飞，得到：

(3)

设定突防机群从距离警戒雷达600 km的位置起飞，Dj取[50 km，220 km]，可以得到无人机起飞时刻t和无人机与警戒雷达距离Dj的变化关系如图3所示。

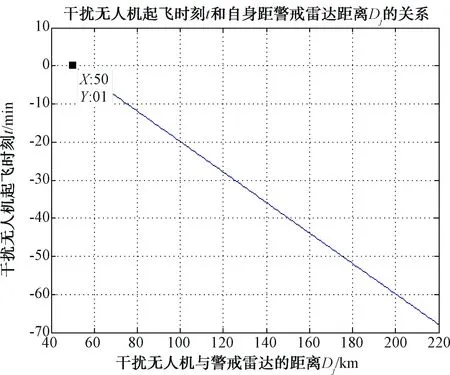
图3 干扰无人机起飞时刻t和自身距警戒 雷达距离Dj的关系图

由图3可知：干扰无人机离警戒雷达越远，起飞时间越早。在以上给定的条件下，当干扰无人机与警戒雷达距离为50 km时，干扰无人机与突防机群同时起飞刚好可以完成任务；但是由于无人机的可回收航程为s=200 km，布置在距警戒雷达20 km处进行干扰，所以最远起飞距离smax=220 km，这就简单地解决了干扰无人机何时起飞能最大效益地完成作战任务的问题。

2 无人机干扰时机规划

无人机形成干扰压制效果应该满足几点要求：(1)在攻击编队进入对方预警探测范围前，无人机就已经到达有效实施干扰的位置，可正常遂行干扰压制任务。(2)在攻击编队返航，脱离对方预警探测范围后，无人机才能终止干扰压制任务[5]。在干扰技术有效的前提下，对雷达的有效干扰时间主要由无人机的飞行性能来保证。无人机以不同的飞行速度飞行时，所能达到的飞行航程和飞行时间是不相同的。

要形成对雷达的有效干扰，干扰能量需要满足下式：

(4)

或写为：

(5)

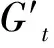
接下来，根据不同的干扰目的讨论雷达对抗无人机干扰的时机[6]。

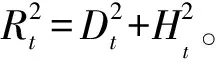
(6)

(7)

(2) 当θ0.5/2<|θ|<90°时，有：

(8)

(3) 当90°≤|θ|≤180°时，有：

(9)

式中：C=K(θ0.5/90)2，为常数。

以雷达为极点，雷达与干扰机的连线为极轴，建立极坐标系。根据上述讨论，以θ为自变量，代入不同的数值，绘出Dt所满足的区域以及Dt所对应的曲线。由曲线可知，它是以干扰无人机和雷达的连线为轴、两边对称于此线的一个心形曲线。于是压制区为该心形曲线之外的区域，而该心形曲线之内的区域为暴露区，突防机群飞入暴露区内将被警戒雷达发现[7]。示意图如图4所示，其中Pt=100 kW，Gt=40 dB，Kj=4，σ=40 m2，Pj=100 W，Gj=10 dB，Vj=0.5，K=0.05，Ht=6 000 m。

图4 突防机群的暴露区示意图

由式(6)，当干扰无人机在20 km处实施干扰时，根据自卫干扰的方程可求得R0=16 km，所以干扰无人机有效干扰时间：

tyx=(Rmax-R0)/v1·60+2

(10)

代入Rmax=380 km、v1=800 km/h、R0=

16 km，得tyx≈30 min。综上可以看出，最大暴露半径在90°≤|θ|≤180°，最小暴露半径在|θ|≤θ0.5/2的范围内。暴露半径受Dj的影响很大，干扰无人机距离雷达越近，暴露区越小，掩护时间越长。突防机群高度Ht对Dt也有较大的影响，当目标高度增加时，暴露区缩小，也就是压制区增大了，此时在无人机的掩护时间相应增加。这是因为此时雷达至目标的距离增大了，而干扰无人机到雷达的距离没有变。

3 结束语

在现有的研究里，对于雷达干扰无人机的研究非常少，针对雷达干扰无人机在作战场景中规划的研究更少，基本没有深入的研究。本文就结合具体的作战场景深入研究2架雷达干扰无人机运用中的时间规划问题，为军事训练提供思路，为以后的研究提供参考，为电子战无人机战术运用提供理论支持[8]。