RPC叠合梁受弯性能试验研究
2019-03-18,*,,
,*,,
(1.桂林理工大学土木与建筑工程学院, 广西桂林541004;2.贺州学院建筑工程学院, 广西贺州542899)
0 引言
叠合梁是建筑工程中常见的一种结构形式,与现浇梁相比,具有施工方便、节约模板、缩短工期等优点;活性粉末混凝土(Reactive Powder Concrete,RPC)具有高强度、高体积稳定性、高耐久性等优良性能[1],因此对活性粉末混凝土叠合梁构件进行研究,具有重要的实际意义。袁海梅[2]对新型叠合梁进行抗弯性能研究,通过与普通混凝土叠合梁比较,新型叠合梁柱节点整体性更好,刚度更大,梁端塑性变形能力更强;朱智俊[3]通过对活性粉末混凝土无粘结预应力叠合梁进行受弯性能分析及承载力计算,研究了部分因素对叠合梁抗弯性能的影响,并建立了活性粉末混凝土叠合梁的抗弯承载力计算公式;张多新等[4]着重分析了二次受力混凝土叠合梁在受力过程中受拉钢筋“应力超前”、后浇混凝土“受压应变滞后”和截面内力转移等的机理;王磊等[5]对6根混凝土叠合梁进行了试验研究,试验研究表明,叠合层强度高一级别的叠合构件基本性能与整体浇筑梁相近,其裂缝条数较多、宽度较大,但并不能明显提高钢筋混凝土梁的屈服弯矩和极限弯矩;胡楚红[6]对普通混凝土和RPC的组合构件进行弯曲受力性能试验研究,推导了组合构件在弯矩作用下的开裂弯矩和正截面承载力计算公式;Hanson[7]试验证明通过对叠合面采取适当的构造措施,可以保证叠合梁的结构强度。
国内外虽然对混凝土叠合梁展开试验和理论研究,但对活性粉末混凝土叠合梁研究较少,需要进一步完善。本文对活性粉末混凝土叠合面高度不同的叠合梁进行抗弯承载力试验,旨在分析研究活性粉末混凝土叠合梁的受弯性能。
1 试验概况
1.1 试件设计
试验制作1根活性粉末混凝土整浇梁和2根活性粉末混凝土叠合梁,梁长均为3 400 mm,试验梁的主要设计参数如表1所示,梁的截面配筋如图1所示。

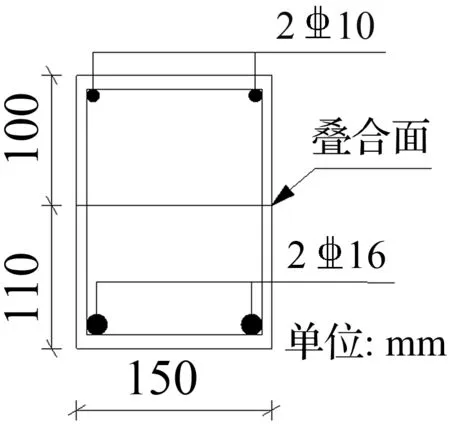
(a) L1 (b) L2 (c) L3

试件编号截面尺寸/mm2箍筋受拉钢筋受压钢筋预制高度h1/mm有效高度比αhL1150×2108@2502162101100.52L2150×2108@2502162101300.62L3150×2108@2502162102101.00
注:有效高度比αh指叠合梁预制截面高度h1与总截面高度h的比值,即αh=h1/h[8]。
1.2 材料性能
参考文献[9],分别在第一次浇筑试验梁和第二次浇筑试验梁的同时各浇筑6个100 mm×100 mm×100 mm立方体试块和3个100 mm×100 mm×300 mm棱柱体试块,与试验梁在同条件下养护28 d,分别测得立方体抗压强度fcu、轴心抗压强度fc和劈裂抗拉强度fts。其中轴心抗拉强度ft= 0.75fts[10]进行换算,其具体数值如表2所示。

表2 活性粉末混凝土力学性测试值Tab.2 Mechanical test value of reactive powder concrete
通过钢筋拉伸试验,得到如表3所示钢筋的力学性能参数。

表3 钢筋力学性能Tab.3 Mechanical properties of reinforcing bars
2 试验现象及分析
2.1 破坏特征
叠合梁与整浇梁的整体破坏特征基本相同,均为适筋破坏,破坏主裂缝均位于纯弯段内。试验梁发生破坏时,纵向钢筋屈服,受压区混凝土未被压碎,原因是叠合梁中纵向受拉钢筋“应力超前”[11],后浇混凝土受压“应变滞后”[12],受拉钢筋达到屈服强度时的荷载较整浇梁显著提前,叠合梁的承载力降低,另一方面活性粉末混凝土抗压强度达到120 MPa以上,远大于试验梁的极限承载力,所以在试验梁破坏时,受压区混凝土没有被压碎。
加载初期,叠合梁跨中区段出现多条竖向裂缝,其宽度和长度都较小,随着荷载的增加缓慢增长;继续加载,弯曲裂缝向上延伸穿过叠合面,并随着荷载的增大不断向上延伸,宽度缓慢增大;当钢筋达到屈服强度时,基本不再出现新裂缝,裂缝宽度不断增大,其中裂缝宽度较大的发展成为主裂缝,最后试件裂缝宽度超过极限值,试件破坏。
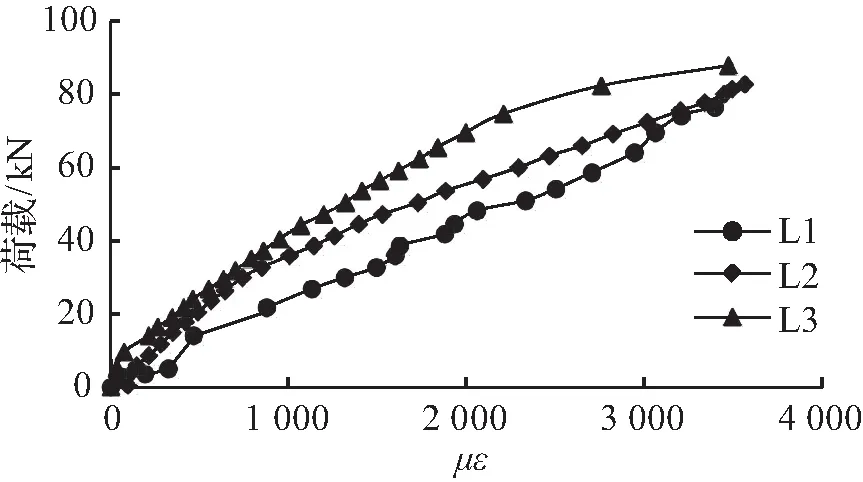
图2 受拉钢筋荷载—应变曲线Fig.2 Tensile reinforcement load-strain curve
2.2 受拉钢筋应力分析
将试验中测量的受拉钢筋应变绘于图2中。
由图2可以看出,在荷载作用下,叠合梁中的受拉钢筋应变增长率显著大于整浇梁,叠合梁中受拉钢筋的应力主要取决于截面有效高度比。由于叠合梁存在应力“超前现象”,叠合梁中的受拉钢筋达到屈服强度时比整浇梁显著提前,叠合梁中受拉钢筋屈服后,直至极限状态,钢筋应变增长很快,使试件的变形和裂缝加快增长。
2.3 裂缝分析
根据在各级荷载下得到各试验梁最大裂缝宽度和平均裂缝间距的数据,分别绘制出如图3和图4所示的曲线图。
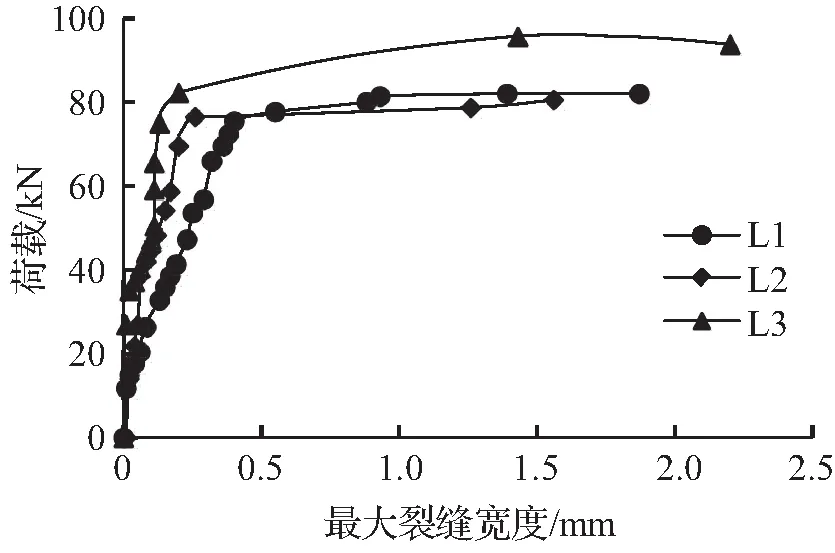
图3荷载—最大裂缝宽度曲线图
Fig.3Load-maximumcrackwidthcurve
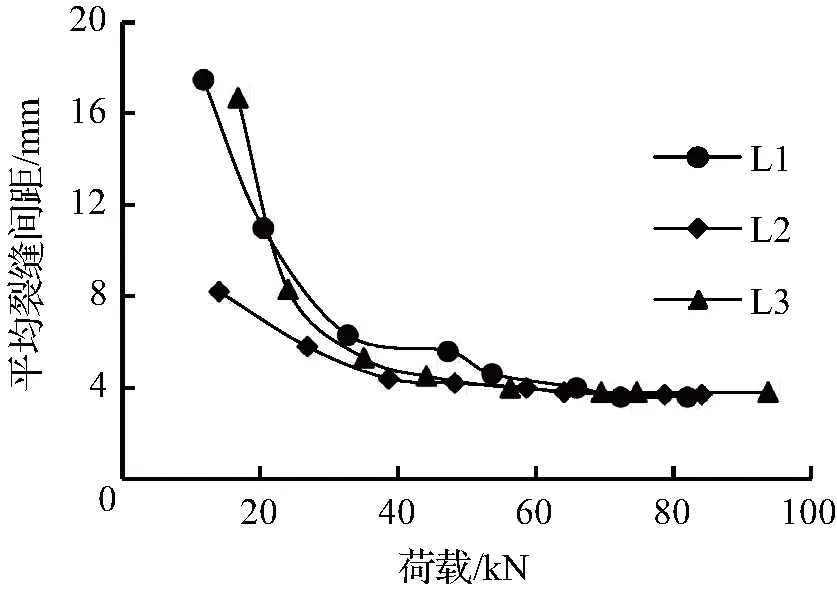
图4荷载—平均裂缝间距曲线图
Fig.4Load-averagecrackspacingcurve
图3反映了各试验梁在荷载作用下最大裂缝宽度的发展规律,可将试验梁主裂缝宽度发展情况分为稳定发展阶段和急速扩张阶段:在稳定发展阶段,最大裂缝宽度随着荷载增大呈线性增长,这是因为在裂缝截面分布大量的钢纤维,钢纤维起到“桥架”的作用,承担裂缝截面上的部分拉应力,抑制裂缝开展和限制裂缝的产生;在急速扩展阶段,裂缝处的钢纤维被拉断或拔出,裂缝宽度迅速增大。各试验梁在裂缝稳定发展阶段,受截面有效高度的影响以及存在超应力现象,叠合梁最大裂缝宽度显著大于整浇梁的裂缝宽度,并随着荷载的增大而扩大其差值。
从图4可以看出,各试验梁的平均裂缝间距变化趋势相似,并且随着荷载的增大而平均裂缝间距不断减小,最后趋于定值。在裂缝发展前期,裂缝数量少,裂缝平均间距较大;在裂缝发展阶段,由于钢纤维的阻裂作用,新裂缝发展较稳定,平均裂缝间距变化趋缓;在接近极限荷载时,裂缝基本“出齐”,不再出现新的裂缝,平均裂缝间距基本趋于定值。对比叠合梁与整浇梁,梁平均裂缝间距变化特征基本一致。
2.4 跨中挠度分析与计算
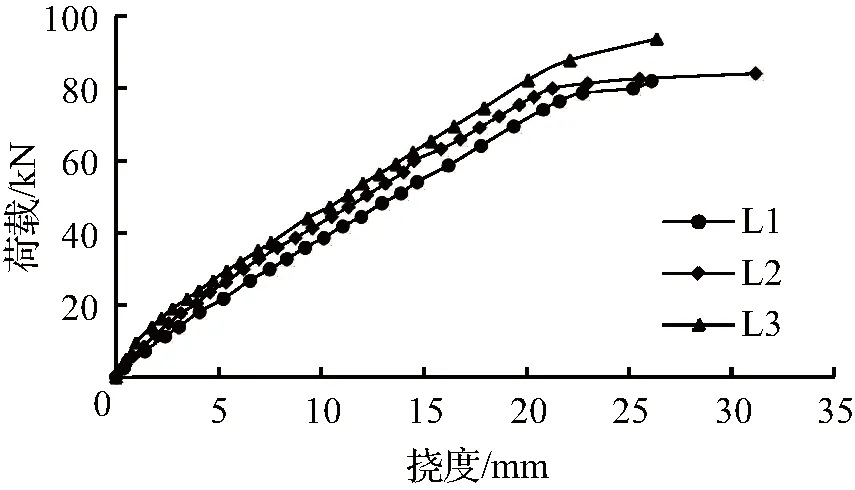
图5 荷载—挠度曲线Fig.5 Load - deflection curve
根据各级荷载下试验梁跨中挠度数据绘制荷载—挠度曲线如图5所示。
从图5看出,整浇梁与叠合梁荷载—挠度曲线趋势基本一致,混凝土开裂前,荷载较小,试验梁处于弹性受力阶段,RPC可以发挥较好的抗拉作用,跨中变形很小,3根试验梁的荷载—挠度曲线基本重合;随着荷载的不断增大,试件进入裂缝稳定发展阶段,荷载—挠度曲线仍呈直线变化,但与第一阶段相比曲线斜率变小,钢纤维的“桥架”作用[13]延缓了裂缝的开展,使得梁的刚度并没有明显减小;在破坏阶段,荷载—挠度曲线有明显的转折点,荷载增加很小值,挠度值却增加很大,在L1和L2中突变愈加明显。相较于整浇梁,叠合梁纵向受拉钢筋应力超前,导致叠合梁的挠度增大,且挠度随着截面的有效截面高度比的增大而减小。
根据平截面假定并结合材料力学的计算方法,计算截面的平均曲率φ和平均刚度Bs,如公式(1)所示,式中RPC的压应变、钢筋的拉应变和曲率均采用平均值。
(1)
式中:rm为平均曲率半径;
Mk为荷载效应标准组合下的弯矩;
Bs为荷载效应标准组合下的短期截面刚度;
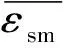

受压区边缘混凝土和受拉区钢筋平均应变按式(2)和式(3)进行计算:
(2)
(3)
取αE=Es/Ec,ρ=As/bh0并综合式(1)~(3)可得:
(4)
式中:ψ为RPC叠合梁裂缝间纵向受拉钢筋的应变不均匀系数;
η为RPC叠合梁裂缝截面处内力臂系数;
ξ为RPC叠合梁裂缝间混凝土应变综合系数;
裂缝间钢筋平均应变与裂缝截面钢筋最大应变的比值为钢筋应变不均匀系数[14]。钢纤维跨越裂缝抑制裂缝产生和限制裂缝扩展,承担了钢筋的部分拉力,使裂缝间钢筋平均应变与裂缝截面钢筋最大应变都相应的减小,故对ψ的影响不大。因此,RPC叠合梁裂缝间纵向受拉钢筋的应变不均匀系数ψ采用与普通混凝土叠合梁相同的公式进行计算:
(5)
式中:Mcr为试验梁开裂弯矩;
M为试验梁正常使用极限弯矩。
考虑不同叠合梁预制高度的影响,参考文献[15],可得:
(6)
(7)
综合各式,得到活性粉末混凝土叠合梁短期刚度计算公式为:
(8)
根据材料力学,可得三分点加载下RPC叠合梁挠度计算公式如(9)所示:
(9)
将试验所得的实测值ωt与通过式(9)计算所得的理论值ωc进行对比,如下表4所示:

表4 试验梁跨中挠度值与理论值对比Tab.4 Comparison of deflection value and theoretical value of test beam span
注:F0.3为试验梁裂缝宽度达到0.3 mm时所对应的荷载,即正常使用极限荷载。
由表4中叠合梁跨中挠度的试验值与计算值的对比结果分析可知,平均值为1.00,标准差为0.027,变异系数为0.027,计算所得的试验梁挠度值与试验实测值吻合较好,说明用式(9)来计算RPC叠合梁挠度是可行的。
2.5 试件延性对比分析
延性是指材料的结构、构件或构件的某个截面从屈服开始到达最大承载能力或到达以后而承载能力还没有明显下降期间的变形能力[16],构件的延性取决于临界截面的延性。本文采用位移延性系数μΔ来衡量叠合梁延性的大小,位移延性系数μΔ为构件极限位移Δu与屈服位移Δy的比值,即:
(10)
各试验梁跨中位移延性系数计算结果如表5所示:

表5 试验梁位移延性系数计算结果Tab.5 Calculation result of displacement ductility coefficient of test beam
从上表5可以看出,整浇梁L3位移延性系数最高,说明整浇梁整体性最好,延性也最好,叠合梁L1、L2的延性系数较整浇梁有所降低,并且随着预制高度的降低延性系数也减小,表明叠合梁预制高度对延性有一定影响。
2.6 承载力对比分析
将试验梁的荷载特征值汇总如下表6所示:

表6 试验梁荷载特征值Tab.6 Load characteristic value of test beam
注:Fcr为试验梁的开裂荷载;Fu为试验梁对应的极限荷载;ΔF为试验梁极限荷载与开裂荷载的差值。
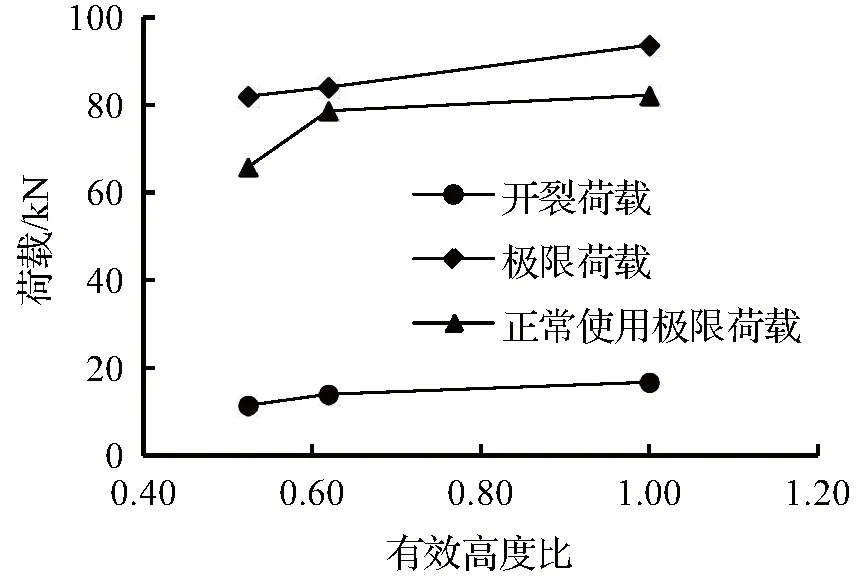
图6 荷载—有效高度比曲线Fig.6 Load - Effective height ratio curve
将荷载特征值绘制成曲线如图6所示。
从表6可以看出,ΔF为极限荷载与开裂荷载的差值,体现了构件开裂后的能力储备值即带裂缝抗弯工作能力,可以发现随着有效高度比的增大,带裂缝抗弯工作能力有所增强。叠合梁较整浇梁抗弯承载力降低,一方面是叠合梁界面层的预压力不同,即有效高度比大,预压力就小;另一方面是由于叠合梁中存在“应力超前”现象,叠合梁中受拉钢筋达到屈服强度时的荷载比整浇梁显著提前。
结合表6和图6,叠合梁的开裂荷载、正常使用极限状态荷载以及承载能力极限荷载都随着预制高度的提高而小幅增加,预制高度从110 mm提高到130 mm和210 mm,叠合梁的开裂荷载分别提高了20 %和46 %,正常使用极限荷载分别提高19 %和25 %,极限荷载分别提高4 %和17 %。预制高度对特征荷载的影响程度从大到小依次为:开裂荷载Fcr、正常使用极限荷载F0.3、极限荷载Fu。叠合梁因存在“应力超前”现象,且有效截面高度比越小,应力超前现象越明显,导致开裂荷载、正常使用极限荷载和极限荷载越小。可以看出,构件在各阶段的荷载值主要受截面有效高度比的影响。
3 结论
① 试验RPC梁在配筋合适的情况下均发生适筋破坏,表现出良好的塑性性能,叠合梁的延性较整浇梁有所降低,随着预制高度的降低延性系数也减小。
② 在达到破坏荷载之前,叠合梁与整浇梁受拉钢筋应力、跨中挠度和裂缝宽度等均有相似的变化趋势。受截面有效高度比的影响,叠合梁在荷载作用下产生的受拉钢筋应力、跨中挠度和最大裂缝宽度等都显著大于整浇梁的相应值。
③ 根据RPC材料的特性,考虑叠合梁不同预制高度的影响,推导出RPC叠合梁跨中挠度的计算建议式,经试验梁验证,吻合度较好。
④ 受“应力超前”和截面有效高度比的影响,叠合梁的开裂荷载、正常使用极限荷载和极限荷载较整浇梁有所降低,且有效截面高度比越小,“应力超前”现象越明显,相应的荷载特征值越小。
