基于FSI效应AP1000屏蔽厂房重力水箱的模态分析
2019-03-18,*,2
,*,2
(1.苏州科技大学土木工程学院,江苏苏州215011; 2.江苏省结构工程重点实验室, 江苏苏州215011)
0 引言
核电站在地震作用下的安全性问题日益受到世界各国的关注,特别是在“福岛核事故”后,各国纷纷对核电站建设进行重新评估[1]。在今天,化石燃料带来污染问题又难以解决和控制,核电作为清洁、高效能源依然得到广泛地提倡。针对其安全问题,各国都对核电技术进行创新升级改造,就目前的三代核电技术而言,西屋公司的AP系列核电技术就是典型代表。它具有相对简单性、安全性和可靠性等特点[2]。其中,非能动安全壳冷却系统(Passive Containment Cooling System,简称PCS)是其主要的安全保障创新之处。PCS由一台与安全壳屏蔽厂房结构合为一体的冷却水重力水箱(以下简称PCS重力水箱)构成。PCS重力水箱位于屏蔽厂房屋顶的顶部,除了给安全壳除热功能外、还起到了在停堆后为消防用重力水箱补水等重要作用[3]。
AP1000核电站的PCS重力水箱是核电站的关键设施,在抗震设计中属于I类设计,与传统水箱的结构形状存在很大区别。在地震作用下,PCS重力水箱内水体发生很大的液固耦合效应(Fluid Structure Interaction,简称FSI),产生很大的晃动力,这种晃动作用可能会影响结构的振动特性[4-5]。目前,许多理论计算、数值模拟、实验分析等方法已经应用在含液容器结构动力求解问题上[6-7],但是这些研究主要集中于石油化工的储液罐、水工建筑的水塔等。
本文采用ANSYS软件,基于液固耦合分析方法,建立PCS重力水箱的耦合有限元模型,通过理论分析方法和有限元数值模拟方法对比,分析不同工况下的低频液体晃动模态,比较理论等效方法与有限元模拟方法差异性大小。再通过有限元法分析高频液体与结构之间相互作用的结构振动模态,研究不同液体高度对结构模态影响。
1 PCS重力水箱的固有特性分析方法
1.1 理论模型液体晃动频率分析方法
液固耦合动力学是解决液体晃动问题重要的理论依据。一般利用Navier-stokes方程积分计算得到解析解,但是这种求解过程往往比较复杂。对于形状较复杂的流动,而又是非线性问题,不能合理简化,往往得不到合理的解析结果[8]。为了更加简便求解,Housner等[9]提出了集中质量模型,如图1所示,假设将流体对箱壁产生的动压力分为脉冲压力和对流压力,其中脉冲压力由不晃动的液体惯性力产生;对流压力由液体晃动产生。用两个与结构连接形式有差异的等效质量的振动来相似模拟这两种动压力,质量M1为脉冲质量,与结构固结,质量M2为振荡质量,用弹簧单元K1与结构固结。一般一阶晃动在结构中占主要作用,可仅考虑第一阶晃动。其中,结构内的液体是无漩不可以压缩的粘性液体。
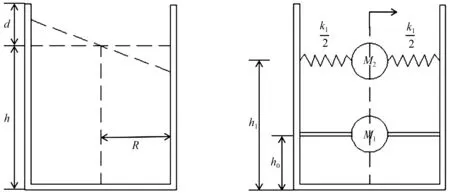
图1 Housner集中质量模型图Fig.1 Housner lumped mass model
对于圆柱形结构的液体容器,运用Housner的理论,可得到其液体晃动的第一阶模态频率,其公式如(1)所示。PCS重力水箱是一个坡底的环状水箱,本文采用的理论方法1是将PCS重力水箱等效成同体积同外径圆柱形水箱计算晃动频率,如图6(a)所示。
(1)
对于环状矩形截面的液体容器,在Housner的理论基础上,美国航天协会通过实验给出液体晃动频率的经验公式,如(2)、(3)所示。PCS重力水箱是一个坡底的环状水箱,本文采用的理论方法2是将PCS重力水箱的等效成截面为矩形且与水箱内、外径相同的环形水箱进行计算晃动频率。如图6(b)所示。
(2)
(3)
式中,n是液体晃动模态的阶数;g是重力加速度;R0是环状容器的外径;hα是等效环形水箱液面高度;νn是相应贝塞尔函数方程的第的根[10],本文v1=1.488。
1.2 FEM模型液体晃动模态分析方法
针对水箱液体晃动有限元分析,液固耦合问题一般采用位移—位移格式,即将流体假设成无剪切刚度的固体。流体通常采用FLUID80单元,该单元是基于Housner理论建立。同时将液固耦合的边界形式采用自由度耦合方式成可滑动边界,最终得到液—固耦合体系质量和刚度矩阵式对称,液固耦合系统特征方程如(4)所示:
([Ks]+[KL]){φ}=ω2([Ms]+[ML]){φ},
(4)
式中:[Ms]、[ML]为结构质量矩阵和液体质量矩阵;
[Ks]、[KL]为结构刚度矩阵和液体刚度矩阵。
为了降低模型的计算规模,通常是采用凝聚缩减方法将有限元模型的自由度缩减为以少量主自由度表示的系统方程。在ANSYS软件中关于模态提取提供多种方法:分块法(Block Lanczos)、缩减法(Reduced/Householder)、非对称法(Unsymmetric)等,其中只有缩减法适合水箱的体内液体晃动模态分析[11]。
1.3 FEM模型耦合系统的结构振动模态分析方法
对于水箱的振动模态分析,用位移—压力格式计算。计算流体时,将液体视为不可压缩、无黏性的理想液体。耦合作用采用是ANSYS中FSI标签设置,有以上假设,再利用伽辽金方法对液体声速波动方程进行分解,最后依据液固耦合的边界条件,可以得到液固耦合作用的矩阵表达式如(5)所示:
(5)



ρ为理想流体的密度;c表示流体的中声速;{Np}T为垂直于矢量{Pe}的近似单元形函数。
可以发现上式矩阵表达式是不对称的刚度矩阵。根据上节所述,在ANSYS中进行耦合系统的结构振动模态分析时,选用非对称法。
2 PCS重力水箱有限元模型建立
2.1 PCS重力水箱有限元模型几何参数及工况
PCS重力水箱位于AP1000屏蔽厂房结构屋顶的上部,如图2所示,是钢筋混凝土结构,它的初始水位是10.8 m。本文通过ANSYS软件建立水箱有限元模型,如图3所示,模型的几何参数如表1所示。

图2AP1000屏蔽厂房有限元模型
Fig.2FEmodelofAP1000shieldedbuildingstructure

图3PCS重力水箱有限元模型
Fig.3FEmodelofthePCSgravitywatertank

表1 屏蔽厂房和重力水箱的几何尺寸Tab.1 Geometric details of the gravity water tank
考虑液固耦合作用,利用ANSYS中模态相应的分析方法,选取PCS重力水箱不同水位高度作为研究对象。本文主要设计5种工况条件,五种工况对应初水位高度的占比分别是100 %,80 %,60 %,30 %,0。其中水箱内的真空高度和水位高度分别用h0和h1表示,“等效圆柱水箱”和“等效环形水箱”的水位高度分别用hc和ha表示。水位高度的工况见表2和图4所示,PCS重力水箱几何剖面图及水位高度见图5所示,等效水箱水位高度如6所示。

表2 不同工况的水位高度Tab.2 Heights of water for different cases

图4PCS重力水箱工况图
Fig.4Differentworkingcasesofthegravitywatertank

图5 PCS重力水箱水位高度图Fig.5 Heights of water level of the gravity water tank

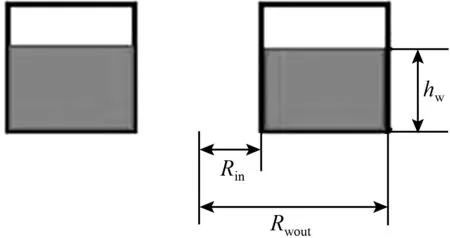
图6等效水箱水位高度图
Fig.6HeightsofwaterleveloftheEquivalentwatertank
2.2 有限元单元材料参数
对于大型PCS重力水箱,对其进行必要结构简化。钢筋混凝土结构采取整体建模方式,ANSYS中将钢筋通过实参数方式等效到混凝土中,即钢筋采用刚度等效方式。本文水平和竖直方向的钢筋配筋率都是8 %[12]。重力水箱采用实体单元进行网格划分。
分别建立不同工况下的水箱的有限元模型,研究晃动模态时,水体采用实体单元FLUID80;研究水箱耦合系统的结构模态时,水体采用实体单元FLUID30。混凝土采用实体单元SOILD65,钢筋通过配筋率表示。其中,假设水箱内的液体是无漩涡、不可压缩的理想流体。具体材料特性取值如下:混凝土弹性模量E=32.5 GPa,泊松比μ=0.2,密度ρ=2 400 kg/m3;流体单元视不同单元设置不同参数,其中流体的弹性模量一般取结构弹性模量的1 %,泊松比取相对很小的值[13]。弹性模量E=2.1 GPa,泊松比μ=0.3×10-4,密度ρ=1 000 kg/m3,热膨胀系数α=5.5×10-6K-1(FLUID80),声速v=1 460 m/s(FLUID30)。
3 PSC重力水箱的模态分析
3.1 重力水箱水晃动频率对比分析
按照本文所述的理论分析方法,根据PCS重力水箱几何尺寸,计算得到的理论结果如表3所示。利用FEM法得到液体的晃动频率,其中第一阶频率结果如表4所示,计算得到的晃动频率偏差结果如表4、5所示,其中偏差计算公式如(6)所示:

(6)
注:工况5水位为零,因此没有液体晃动。
将PCS重力水箱中的液体以同体积形式等效成圆柱形水箱、环形平底水箱中液体后,等效水箱的水位高度相对原结构都降低,虽然圆柱形水箱水位高度的降低量相比环形平底水箱的大很多,但是从表4中的晃动频率偏差分析中发现,两者的晃动频率相差不大,最大相差没有超过5 %,满足工程上要求。同样,随着水箱里水位的升高,水的晃动频率增大,即液体的晃动的周期在变短。

表4 理论方法1和理论方法2水的晃动频率的比较Tab.4 Comparison of sloshing frequencies of water by theoretical method 1 and theoretical method 2
注:工况5水位为0,因此没有液体晃动。
由表4偏差δ1可知,在理论方法中,本文方法1计算得到PSC重力水箱水晃动频率与本文方法2计算结果相差非常小,本文方法1和2的水晃动频率的偏差大小随着水位升高,也是呈减小趋势。高水位情况下基本一致。本文方法1相对本文方法2计算过程更加简便。若两者准确性相当时,特别是高水位的情况,建议采用本文方法1。
与有限元计算结果对比中发现,理论方法与FEM法计算得到的晃动频率相差较大,尤其是低水位时,偏差30 %左右,从偏差δ2和偏差δ3中发现,本文方法1和本文方法2与FEM法的结果偏差较相近,同时也是随着水位降低,偏差增加。从而得出,高水位时,理论法与有限元法可信度相当。偏差原因主要以下几点:①在低水位时(工况4),相比前几个工况液体自由液面宽度发生了改变,液体剖面几何形状的改变与理论法中液体剖面形状相差较大,即它们的外液面边界宽度不一致;②理论公式中没有真正考虑液—固耦合之间的动力相互作用,耦合作用只是通过弹簧与结构固定连接,而有限元中耦合作用是选择自由度耦合方法建立可滑动边界来表示;③由于许多的简化处理给理论值和数值仿真模拟值带来的偏差,例如:理论方法中是将流体简化成单个脉冲质量和对流质量单元,有限元则是离散成有限的网格质量单元,两者质量单元上数量有差异,造成计算精度差异等。

表5 FEM法与理论方法水的晃动频率的比较Tab.5 Comparison of sloshing frequencise of water by FEM and theoretical methods
注明:工况5水位为0,因此没有液体晃动。
3.2 PCS重力水箱水晃动模态FEM结果分析
表6给出了不同液面高度时液体晃动频率的有限元解,当工况4时,FEM法与理论方法相差过大,在这里不进行考虑。

表6 不同水位下重力水箱结构晃动频率对比Tab.6 Comparison of sloshing frequencies of gravity water tanks under different water levels
从表6中发现,每一个工况下,晃动频率随着水位高度增加而增加,液体晃动参与的质量也是随着水位高度增加而增加的。晃动频率中出现了部分阶的频率重叠现象,例如第一阶和第二阶晃动频率相同。每一个工况下,晃动频率的增长的速率也不一致,第一阶、第二阶、第六阶、第七阶、第八阶晃动频率增加速率是比较接近,其他则相差较大。液体晃动频率值都是比较小,较小频率的波动会引起液体的晃动,但是液体质量越大,共振波动需要的共振频率越大。
3.3 PCS重力水箱液固耦合结构的振动模态分析
图7给出五种工况下前六阶固有频率。因上节分析晃动频率时,水位越高,与理论结果越接近,图8给出有代表性的空水箱(工况5)和初水位(工况1)前20阶固有频率变化。
由图7可知,PCS重力水箱的液固耦合系统频率随着水位变化很大,水位越高,频率下降越大,说明液固耦合作用使得结构频率下降,同时也表明同样的耦合作用在结构中作用明显。由图8看出,在水箱中,空箱(工况5)和初水位10.8 m(工况1)有着明显区别,且两者频率增加几乎呈现线性。

图7水位高度与阶数频率的关系图
Fig.7Relationshipbetweentheheightsofwater

图8结构模态变化曲线图
Fig.8Curvegraphofstructuralmodal
4 结论
本文采用ANSYS软件,建立AP1000屏蔽厂房PCS水箱有限元模型,主要针对低频晃动与高频液体和结构耦合作用的模态进行分析,模拟了不同工况下水箱中水晃动的动力特性,并与现有理论公式的等效计算结果进行对比分析,也对比了在液固耦合作用下不同工况的结构固有特性的变化情况。主要结论汇总如下:
① 基于不同理论分析方法,屏蔽厂房结构PCS水箱液体晃动模态分析时,本文方法1和本文方法2结果相近,建议采用本文方法1,计算过程简单。运用规则的容器理论计算公式套用非规则容器晃动时,可提高计算效率,但是带来的误差需要考虑,应当给出其他较精确的研究手段进行验证,本文借用有限元模拟进行辅助验算。
② 基于理论分析与有限元模拟对比,有限元方法的结果普遍比理论值偏小,两者都反应出水的晃动频率随水位在升高,理论法变化平稳,而有限元变化较“陡峭”。同时,当水箱里水位变化,晃动频率发生改变,水箱相应的水晃动比例发生变化,与之相应的水冲动比例也会变化,从而导致结构动力响应发生变化。
③ 屏蔽厂房结构的PCS重力水箱液固耦合系统的结构频率在不同水位高度有着一定的差异,水位越高,固有频率越小。因此,在地震时,需要考虑水箱一旦运行,水位发生改变,液固耦合作用将影响到结构的地震响应变化,从而为研究结构在水箱的FSI效应下减震水位和不利水位提供方向。
④ 对于PCS重力水箱这种类似刚体水箱结构,其在低频段,水体的晃动就易被激发,而结构的变化不是很大,而高频段时结构和液体耦合作用明显。
