内埋空间钢构架方形钢管混凝土短柱轴压承载力计算

，*，,

(1.苏州科技大学土木工程学院， 江苏苏州215011；2.中衡·苏州华造建筑设计有限公司， 江苏苏州215021)

图1 内埋空间钢构架方形钢管混凝土柱截面形式Fig.1 Cross section of square steel tubular concrete column filled spatial steel frame

0 引言

已有的研究表明[1-11]，方钢管对核心混凝土，空间钢构架对核心混凝土均能产生一定的约束作用，能够提高核心混凝土的抗压强度和变形能力。但是在轴向压力作用下方钢管混凝土短柱达到峰值荷载以后，承载力衰减速度和幅值较大，没有圆形钢管混凝土柱的性能好。空间钢构架混凝土短柱达到峰值荷载以后，承载力下降速度和幅值较为平缓，变形能力相对较好，但在轴向压力作用下空间钢构架的角钢容易发生压曲，致使角钢不能充分发挥作用。为了改善方形钢管混凝土柱的轴压性能，克服空间钢构架存在的不足，提出一种新型的内埋空间钢构架方形钢管混凝土组合柱(图1)，这种组合柱具有空间钢构架约束核心混凝土，方形钢管约束空间钢构架外侧混凝土的双重约束作用，这一特征能够有效提高组合柱的承载力和变形能力。国内外学者开展了内埋实腹式钢骨钢管混凝土组合柱的研究[12-15]，但对内埋空间钢构架钢管混凝土组合柱的研究还很少，为了探索内埋空间钢构架方形钢管混凝土柱轴压性能，本课题组进行了5个内埋空间钢构架方形钢管混凝土轴压短柱试验研究[16]，在此基础上，分析了内埋空间钢构架方形钢管混凝土轴压短柱的混凝土约束机理，并考虑混凝土的双重约束作用，提出了两种内埋空间钢构架方形钢管混凝土短柱轴压承载力的计算方法，其计算值与试验值符合较好，可以作为这种新型组合柱轴压承载力的计算公式。

1 内埋空间钢构架方钢管混凝土约束机理分析

已有的研究表明[1]，方形钢管对核心混凝土存在约束作用，角部区域和核心部位为约束区，截面边缘中间为非约束区，如图2所示。已有的研究表明[6-11]，空间钢构架对核心混凝土存在一定的约束，角钢区域和核心部位为约束区，角钢之间在截面边缘为非约束区，且沿柱高度方向在横向缀条部位约束较强，在横向缀条之间约束相对较小，如图3所示。将空间钢构架埋入方形钢管混凝土柱中核心部位形成内埋空间钢构架方形钢管混凝土柱。空间钢构架对核心混凝土具有约束作用，而空间钢构架外侧混凝土受到方形钢管的约束作用，图4给出了峰值荷载时内埋空间钢构架方形钢管混凝土柱截面混凝土的Mises应力云图。

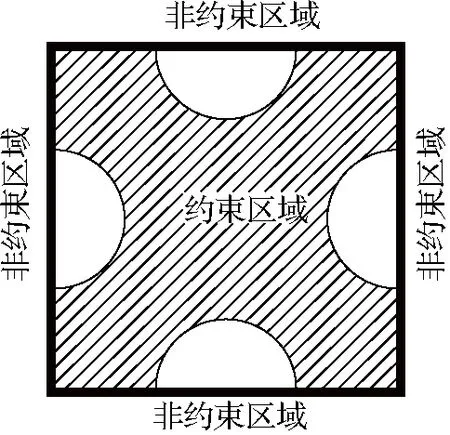
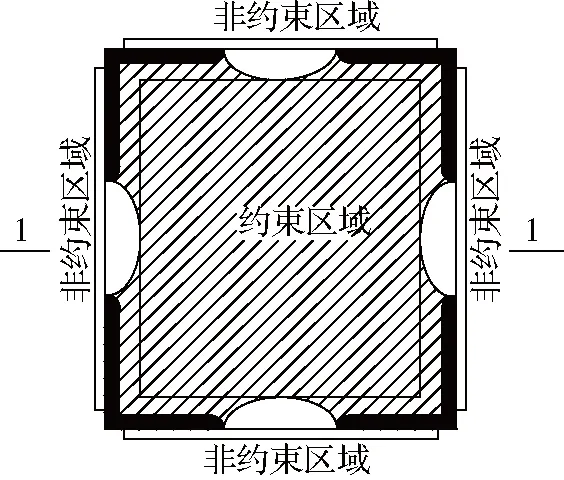
图2方钢管约束混凝土示意
Fig.2Constrainconcreteofsquaresteeltube

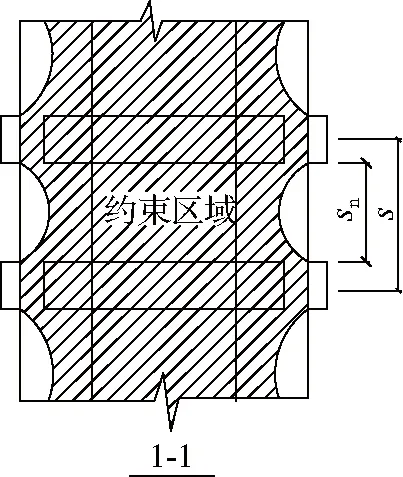
图3空间钢构架约束混凝土示意
Fig.3Constrainconcreteofspatialsteelframe

(a) 空间钢构架外混凝土 (b) 空间钢构架核心混凝土

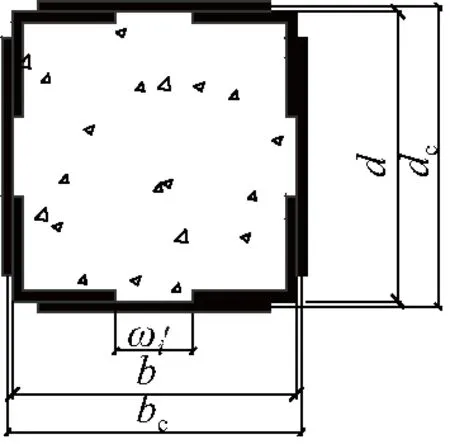
根据图4截面混凝土Mises应力云图和参考文献[1]、文献[11]，假定空间钢构架外侧混凝土的非约束区域为半圆形(直径Dc-bc或Dc-dc)，如图5(a)所示。假定空间钢构架内侧混凝土的非约束区域为抛物线，水平线与非有效约束区域抛物线切线的夹角为45°，如图5(b)所示。

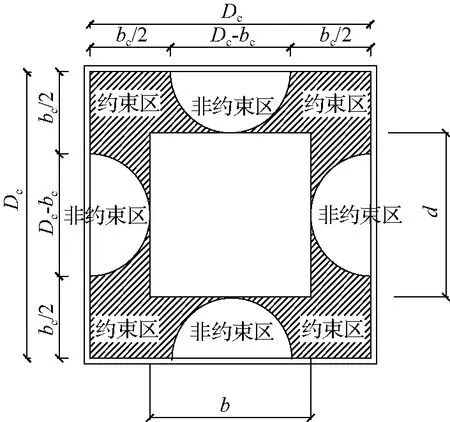
(a) 空间钢构架外侧混凝土约束 (b) 空间钢构架内侧混凝土约束

由图5(a)可得，空间钢构架外侧混凝土的非约束区域截面面积Ac1和约束区域截面面积Ac2分别按下式计算：

(1)

(2)

式中，Ak为空间钢构架混凝土柱截面面积，Ak=b×d。

由图5(b)可得，每个边长方向的非约束区域面积为(ωi′)2/6，ωi′为两个相邻角钢之间的净距离。4个边长方向的非约束混凝土区域的总面积为：

(3)

考虑到纵向相邻角钢之间和横向相邻缀条之间混凝土的非约束区域，沿柱高方向相邻缀条的中间高度截面上的有效约束面积为：

(4)

式中，bc、dc分别为两对边缀条的形心线之间的距离；s为缀条间距；d为缀条宽度。

当内埋空间钢构架混凝土截面为方形时，bc=dc，式(4)可以简化为：

(5)

令空间钢构架混凝土的有效约束系数ke=Ae/Acc，Acc为缀条形心包含的混凝土截面面积，Acc=bc×dc(缀条形心包含的核心截面面积)-Asa(空间钢构架角钢截面面积)，则

(6)

式中，ρcc为空间钢构架角钢截面面积(Asa)与缀条形心包含的核心截面面积(bc×dc)的比值，即ρcc=Asa/(bc×dc)。

2 内埋空间钢构架方形钢管混凝土短柱轴压承载能力计算

2.1 计算方法一

2.1.1 基本假定

① 不考虑钢管、空间钢构架与混凝土之间的滑移。

② 考虑空间钢构架对核心混凝土的约束作用，考虑方形钢管对空间钢构架外混凝土的约束作用。

③ 内埋空间钢构架方形钢管混凝土柱分解为内埋空间钢构架混凝土柱和中空方形钢管混凝土柱两部分，如图6所示。假定内埋空间钢构架方形钢管混凝土短柱轴压承载力(Nu)为上述两部分承载力之和，即

Nu=Nu1+Nu2，

(7)

式中，Nu1为空间钢构架混凝土短柱轴压承载力；Nu2为中空方形钢管混凝土短柱轴压承载力。

④ 不考虑方形钢管，空间钢构架角钢的局部压曲的影响。

(a) 内埋空间钢构架方形钢管混凝土柱=(b) 中空方形钢管混凝土柱 +

(c) 空间钢构架混凝土柱

图6内埋空间钢构架方形钢管混凝土短柱截面
Fig.6Crosssectionofsquaresteeltubularconcreteshortcolumnfilledspatialsteelframe

2.1.2 空间钢构架混凝土短柱轴压承载力Nu1计算

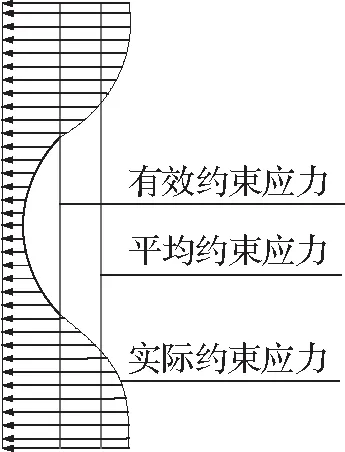
为了将角钢和缀条对混凝土的实际侧向约束作用进行简化等效，假定侧向约束应力为均匀分布(图7(a))，根据力的平衡可得(见图7(b))：

2fyvAss1=(σr1·s)bc，

(8)

2fyvAss1=(σr1·s)dc。

(9)

(a) 侧向约束应力分布 (b) 角钢和缀条隔离体

将式(8)与式(9)相加，整理可得空间钢构架的平均侧向约束应力σr1为

(10)

式中：fyv为空间钢构架缀板的屈服强度；s为缀条的间距；Ass1为缀板的截面面积。

空间钢构架的有效约束应力σr1′：

σr1′=ke×σr1。

(11)

在约束作用下混凝土的轴心抗压强度σcc1可按下式计算：

σcc1=fc+σr1′。

(12)

将式(10)、式(11)代入式(12)得：

(13)

内埋空间钢构架混凝土短柱轴压承载力Nu1：

Nu1=σcc1Ac+fsaAsa，

(14)

式中，Ac为空间钢构架缀条形心包含混凝土截面面积，Ac=bc×dc-Asa；Asa为空间钢构架角钢截面总面积；fsa为角钢抗压屈服强度。

2.1.3 中空方形钢管混凝土短柱轴压承载力Nu2计算

中空方形钢管混凝土短柱轴压承载力Nu2由方形钢管的承载力(Asfs)、非约束区混凝土轴压承载力(fcAc1)和约束区混凝土轴压承载力(σcc2Ac2)之和，即

Nu2=fcAc1+σcc2Ac2+fsAs，

(15)

式中，Ac1为非约束区域混凝土截面面积，按式(1)计算；fc为单向受压时混凝土抗压强度；Ac2为约束区域混凝土截面面积，按式(2)计算；σcc2为方形钢管约束混凝土的峰值应力；As为方形钢管截面面积；fs为方形钢管抗压屈服强度。

采用文献[2]提出的方钢管约束混凝土的峰值应力σcc2来代替约束区域混凝土的抗压强度，即

(16)

式中，ξ为方钢管约束效应系数，ξ=fsAs/fck(A-Ak-As)。

2.1.4 内埋空间钢构架方形钢管混凝土短柱轴压承载力Nu计算

根据基本假定(4)，将式(14)和式(16)代入式(7)可得内埋空间钢构架方形钢管混凝土短柱轴压承载力Nu：

Nu=(σcc1Ac+fsaAsa)+(fcAc1+σcc2Ac2+fsAs)。

(17)

表2给出了根据材料实际力学指标(见表1)，按式(17)计算的本课题组进行的5个内埋空间钢构架方形钢管混凝土短柱试件的极限承载力计算值(Nucal)与试验值(Nutest)。由表2可知，试验值与计算值基本吻合，5个试件计算值与试验值比值(Nucal/Nutest)的平均值为1.004，均方差为0.030。说明该公式可以较好的计算内埋空间钢构架方形钢管混凝土短柱的极限承载能力。

表1 材料力学指标Tab.1 Material mechanical index

注：混凝土立方体抗压强度为38.7 MPa，棱柱体抗压强度为28.5 MPa，混凝土弹性模量为32 018 MPa。

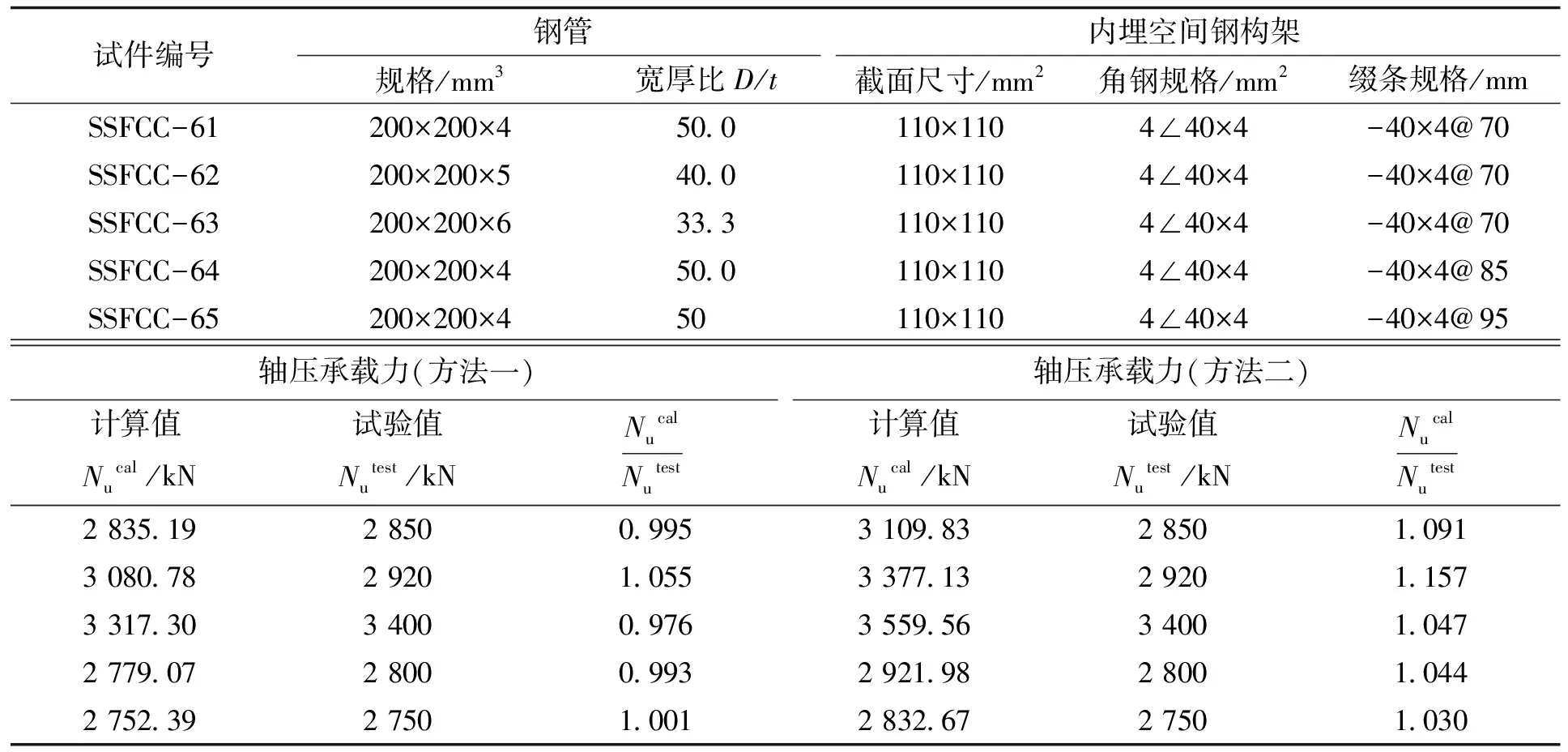
表2 各试件轴压承载力计算值Tab.2 Calculation value of axial bearing capacity of each specimen

2.2 计算方法二

基本计算假定同方法一。

由基本假定(3)可得，内埋空间钢构架方形钢管混凝土短柱轴压承载力(Nu)为内埋空间钢构架混凝土柱轴压承载力(Nu1)和中空方形钢管混凝土柱轴压承载力(Nu2)之和，即Nu=Nu1+Nu2。

由基本假定(1)可知，不考虑钢管与内部混凝土，空间钢构架与内外混凝土的滑移。在轴向力作用下，内部空间钢构架混凝土柱与外部方钢管混凝土柱的纵向变形协调。空间钢构架混凝土短柱的轴向压缩量(ΔL1)与中空方钢管混凝土短柱的轴向压缩量(ΔL2)相等，

ΔL1=ΔL2。

(18)

(19)

将式(19)代入式(7)可得

(20)

式中，E1A1为空间钢构架混凝土短柱的轴向抗压刚度，按下式计算：

E1A1=EsaAsa+EcAc,in，

(21)

式中，Esa、Asa分别为空间钢构架角钢的弹性模量和截面面积；

Ec、Ac,in分别为内埋空间钢构架混凝土短柱混凝土弹性模量和截面面积，Ac,in=Ac-Asa。

E2A2为中空钢管混凝土短柱轴向抗压刚度，按下式计算：

E2A2=EsAs+EcAc,out，

(22)

式中，Es、As分别为钢管的弹性模量和截面面积；

Ec、Ac,out分别为中空钢管混凝土短柱混凝土弹性模量和截面面积，Ac,out=A-Ak-As。

将式(21)和式(22)代入式(20)可得：

(23)

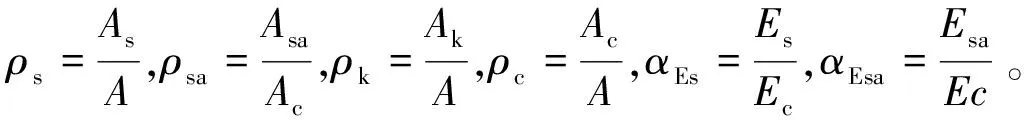
式(23)可整理得：

(24)

将内埋空间钢构架混凝土短柱轴压极限承载力Nu1[式(14)]代入上式，可得内埋空间钢构架方形钢管混凝土短柱轴压承载力计算公式：

(25)

表2给出了根据材料实际力学指标(见表1)，按式(25)计算的本课题组进行的5个内埋空间钢构架方形钢管混凝土短柱试件的极限承载力计算值(Nucal)与试验值(Nutest)。由表2可知，5个试件计算值与试验值比值(Nucal/Nutest)的平均值为1.074，均方差为0.042。说明该公式同样可以较好的计算内埋空间钢构架方形钢管混凝土短柱的极限承载能力。

3 结论

① 内埋空间钢构架方形钢管混凝土柱的混凝土具有空间钢构架对核心混凝土、以及方形钢管对空间钢构架外混凝土的双重约束作用，在分析的基础上，提出了内埋空间钢构架方型钢钢管混凝土柱混凝土的约束机理。

② 考虑内埋空间钢构架方形钢管混凝土柱混凝土的双重约束作用，建立的两种不同计算模型的轴压承载力计算公式，计算值与试验值符合较好，可以用作这种新型组合柱的轴压承载力计算。