带约束拉杆十形钢管混凝土短柱承载力统一解

，，，

(长安大学建筑工程学院， 陕西西安710061)

0 引言

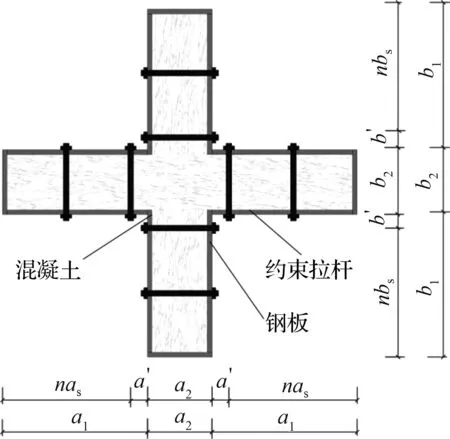
图1 带约束拉杆十形钢管混凝土截面Fig.1 Section of cross-shaped concrete filled steel tube with binding bars

异形截面钢管混凝土柱具有截面惯性矩大、与梁连接方便、易符合建筑平面要求等特点[1-4]，在高层和超高层建筑中具有广泛的应用前景。十形截面是各异形截面中常用的截面形式，与圆形截面相比，十形截面钢管混凝土柱外钢管对核心混凝土的约束在截面上各点是不均匀的，角部约束远强于周边中部约束；外钢管处于纵向、环向以及核心混凝土向外膨胀作用的三向应力状态，容易在屈服前发生局部屈曲[5-7]。带约束拉杆十形钢管混凝土柱是在十形截面的四个分支分别设置一定数量的约束拉杆(见图1)，从而延缓混凝土的外凸变形和外钢管的局部屈曲，有利于承载力和延性的提高[8]。

目前，国内外学者对各种带约束拉杆钢管混凝土柱均有研究。蔡健等[6-10]通过实验对不同截面带约束拉杆钢管混凝土短柱的应力—应变曲线关系、刚度及延性等进行了系统的研究，并在此基础上提出了带约束拉杆矩形钢管混凝土短柱的承载力计算公式。赵均海等[11]对带约束拉杆矩形钢管混凝土短柱进行了理论分析，并提出了简化的承载力计算公式。以上研究中大多采用混凝土五参数破坏准则，计算过程复杂且对十形截面没有得到可直接应用于工程的承载力计算公式，对矩形截面的简化计算方法大多基于试验回归总结得到与拉杆有关的承载力提高系数，缺乏理论依据且不易推广。

本文基于统一强度理论[12]，将带约束拉杆十形截面划分为5个不同的矩形区域，将拉杆和外钢管对混凝土的约束等效为有效侧向应力，同时将各矩形核心混凝土区域合理等效为圆形区域，建立带约束拉杆十形钢管混凝土短柱的轴压承载力计算公式。在此基础上，引入与长细比和偏心率有关的承载力降低系数，得到了带约束拉杆十形钢管混凝土短柱偏压承载力计算公式。

1 统一强度理论

统一强度理论是俞茂宏在1991年建立的考虑中间主应力的影响，并且可以适用于不同材料的强度理论，其表达式为[12]

(1a)

(1b)

(1c)

式中：F、F′为强度理论函数；σ1、σ2、σ3为三个主应力，且σ1>σ2>σ3；σc、σt、τs分别为材料的压缩强度、拉伸强度和剪切强度；α为材料的拉压比；b为反映中间主应力效应的材料参数；B为剪应力系数。

2 极限承载力分析

2.1 受力机理

已有研究表明，带约束拉杆十形钢管混凝土柱可以看作由复合箍筋矩形截面混凝土柱演变出的新型构件[7]，钢管可看作箍筋密排且与纵筋合一，处于复杂的三向应力状态，但由于径向受力较小，可以忽略[8]。约束拉杆可看作复合箍筋中的拉结钢筋，通过约束外钢管的变形约束核心混凝土，因此利用Mander等效侧向应力法[13]分析约束拉杆和钢管对混凝土的约束作用是合理的。核心混凝土受钢管和拉杆的约束处于真三轴受力，基于材料力学理论及面积等效的方法[14]，将核心混凝土简化为常规三轴受力，并考虑中间主应力对核心混凝土强度的提高作用，研究带约束拉杆十形钢管混凝土柱的承载力，其研究方法更符合构件的真实受力。

2.2 截面划分

带约束拉杆十形钢管混凝土柱可利用截面划分后叠加的方法进行研究。本文将带约束拉杆十形截面划分为1个无拉杆的矩形区域(区域“1”)和4个带拉杆的矩形区域(区域“2”～区域“5”)[8](见图2)，并假设各截开面处侧向刚度无限大，截开面处法向位移为零，纵向和法向均满足变形协调条件。

2.3 核心混凝土的侧向平均约束应力

约束拉杆对核心混凝土的约束作用是通过其约束钢管的侧向变形得以实现的[9]。当带约束拉杆钢管混凝土柱达到极限承载力时，柱中位置的约束拉杆也会到达屈服状态[10]。假设核心混凝土各边所受的侧压力均匀分布[10]，在各分开区域取隔离体，长度为拉杆的纵向间距bs，由力学平衡条件分别计算各边的侧向平均约束应力。

对区域“3”(区域“5”)，矩形钢管在水平方向长边、短边受力情况如图3所示。

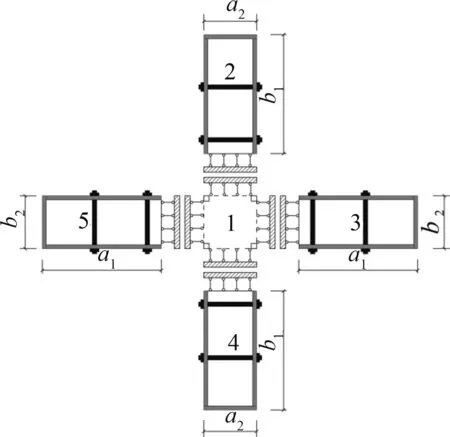
图2带约束拉杆十形截面分区与截开面约束
Fig.2Subregionsofcross-sectionwithbindingbarsandsectionconstraints

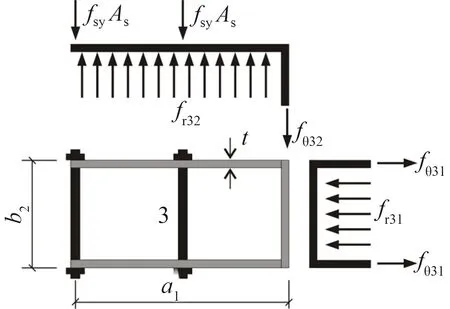
图3矩形区域外钢管侧向受力图
Fig.3Stressofsidedirectiononsteeltubeinrectangulararea

由力平衡条件可得，短边的侧向平均约束应力为：

(2)

长边的侧向平均约束应力为：

(3)

同理对区域“2”(区域“4”)，短边的侧向平均约束应力为：

(4)

长边的侧向平均约束应力为：

(5)

图4 区域1混凝土侧向受力图Fig.4 Stress of side direction on concrete in area 1

式中：ai、bi为构件的截面尺寸(i=1, 2)，由图2确定；fθi1为“i”区域钢管长边的环向应力，fθi2为“i”区域钢管短边的环向应力，fri1为“i”区域短边的侧向平均约束应力，fri2为“i”区域长边的侧向平均约束应力(i取2～5)；As为拉杆截面面积；fsy为拉杆屈服强度；as为拉杆横向间距；bs为拉杆的纵向间距；t为外钢管厚度。

对区域“1”，由截开面处混凝土的应力连续条件，其所受的侧向约束力如图4示。

由力学平衡条件可得，平行于b2边的侧向平均约束应力为：

(6)

平行于a2边的侧向平均约束应力为：

(7)

2.4 核心混凝土的侧向有效约束应力

矩形截面核心混凝土所受的侧向约束主要集中在阳角，其余部分约束相对较弱[10]。参考Mander等效侧向应力法[13]，将矩形截面划分为有效约束区和非有效约束区，以核心混凝土横截面和侧面的有效约束系数反映不同区域所受的不同约束。

在以上研究成果的基础上，对划分所得的5个区域分别利用Mander等效侧向应力法，并作合理假设[8]：

① 各分支截面上拉杆均匀布置且内侧拉杆位于截开面处。

② 横截面和侧面有效区和非有效区的界限为1.5次方的抛物线。

③ 截开面处为强约束边界，不存在横截面和侧面的非有效区。

各区域横截面、侧面上有效约束区和非有效约束区划分如图5所示。

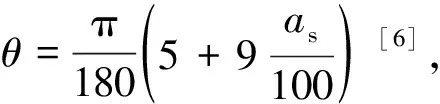
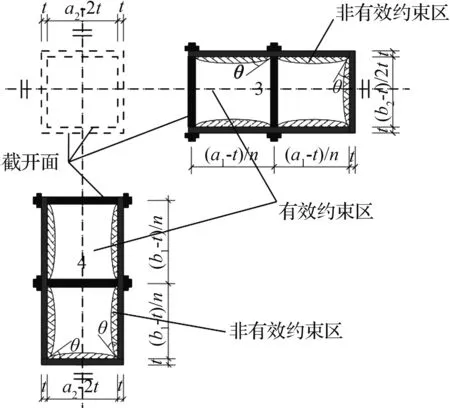
(a) 核心混凝土横截面有效约束区

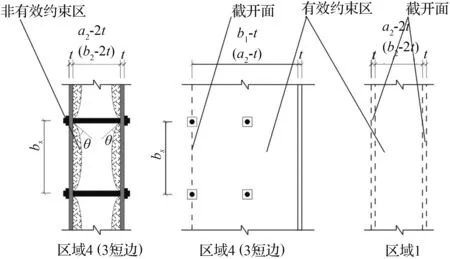
(b) 核心混凝土侧面有效约束区

将截面核心混凝土的有效约束面积与核心混凝土净面积之比定义为该截面的有效约束系数[13]。由文献[8]的研究成果，区域“i”(i取1～5)横截面有效约束系数kesi为：

kes1=1

(8)

(9)

(10)

式中：nsi为“i”区域长边被拉杆分隔成的段数(i取1～5)，当无拉杆时取nsi=1。

区域“i”(i取1～5)侧面有效约束系数keli为：

kel1=1,

(11)

(12)

(13)

对于无拉杆的试件，由于不存在侧面非约束区，取keli=1。

各区域的有效约束系数为横截面与侧面有效约束系数的乘积[13]：

kei=kesikeli(i=1～5),

(14)

式中：当kei≤0(i取1～5)时，取kei=0

设Frij为“i”区域某边上的侧向有效约束应力，由Mander等效侧向应力法[13]可得：

Frij=keifrij

(15)

式中：i取1～5，j取1、2；Fri1为“i”区域长边的侧向有效约束应力；Fri2为“i”区域短边的侧向有效约束应力。

2.5 核心混凝土的轴压强度

研究表明[14-16]，当截面面积相等且含钢率相同时，矩形截面钢管混凝土柱可等效为圆形截面钢管混凝土柱。本文将上述5个矩形区域等效为圆形区域，各区域等效圆钢管有效侧向应力为：

(16)

式中：R、r分别为等效圆钢管的外径和内径，i取1～5。

由aibj=πR2和(ai-2t)(bj-2t)=πr2可得：

(17)

将式(6)、(7)、(15)和(17)代入式(16)，得区域“1”等效圆钢管有效侧向应力：

(18)

将式(2)、(3)、(15)和(17)代入式(16)，得区域“3”等效圆钢管有效侧向应力：

(19)

将式(4)、(5)、(15)和(17)代入式(16)，得区域“4”等效圆钢管有效侧向应力：

(20)

等效圆钢管混凝土柱核心混凝土的应力状态为0>σ1=σ2>σ3，核心混凝土强度由于外钢管及拉杆的套箍作用而得到提高，取σ1=σ2=σr，比较公式(1a)、(1b)，并引入混凝土黏聚力c和内摩擦角φ，则有：

F′-F=b(τ23+σ23sinφ-τ12-σ12sinφ),

F′-F=b(1-sinφ)(σ1-σ3)≥0,

因此取式(1b)得:

F′=τ13+bτ23+sinφ(σ13+bσ23)=(1+b)csinφ,

将上式写成主应力形式并考虑σ1=σ2，得:

将上式简化可得：

(21)

σ3=fc+kσ1。

(22)

将以上研究成果应用于已等效为圆钢管的5个区域，同时考虑到等效圆钢管对核心混凝土的约束强于矩形钢管[15]，引入混凝土强度降低系数γu，可得区域“i”核心混凝土的抗压强度为：

σ3i=fc+γuikσri，

(23)

式中：σ3i为区域“i”(i取1～5)核心混凝土的抗压强度；fc为核心混凝土的单轴抗压强度；k为侧压力系数，取值一般为1.5～7[17]；γui为区域“i”的混凝土强度降低系数，取γui=1.67Di-0.112[16]；Di为区域“i”等效圆钢管的直径，计算时取外径。

将式(18)、(19)、(20)分别和(17)代入式(23)中，可得各区域核心混凝土的抗压强度。

区域“1”核心混凝土的抗压强度为：

(24)

区域“3”(区域“5”)核心混凝土的抗压强度为：

(25)

区域“2”(区域“4”)核心混凝土的抗压强度为：

(26)

2.6 外钢管的应力

在轴向压力作用下，矩形钢管混凝土柱外钢管处于纵向和径向受压而环向受拉的三向应力状态，但由于径向应力远小于纵向和环向应力，因此可不考虑径向应力的影响[10]。钢管的屈曲模态主要与钢管的宽厚比参数R有关[18]。当R≥0.85时，试件发生局部屈曲，R≤0.85时，可不考虑局部屈曲。

为了考虑屈曲模态对钢管横向与纵向强度的影响，分别定义带约束拉杆十形钢管混凝土短柱各边的宽厚比参数为：

(27)

式中：μ分别取a、b；j取1、2；fay、Ea、ν分别为钢管的屈服强度、弹性模量和泊松比。

钢管各边的纵向应力flij和横向应力fθij(i取1～5；j取1、2)可按以下方式确定[10]。

Rμj≤0.85时，fθij=0.19fay；flij=-0.89fay，

(28)

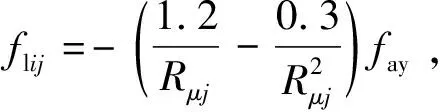
(29)

2.7 轴心受压承载力计算公式

带约束拉杆十形钢管混凝土短柱轴压承载力N即为区域“1”至区域“5”的核心混凝土极限承载力与外钢管极限承载力之和，即：

(30)

式中：Asij为“i”区域“j”边的截面面积(i取2、3、4、5；j取1、2)。

2.8 偏心受压承载力计算公式

带约束拉杆十形钢管混凝土柱偏心受压承载力的计算是在轴心受压的基础上考虑构件长细比和偏心率对承载力的影响。本文在式(30)基础上，取：

(31)

式中：Np带约束拉杆十形钢管混凝土短柱偏心受压承载力，φl为考虑长细比的承载力降低系数，φe为考虑偏心率的承载力降低系数。参考文献[19]对圆形钢管混凝土柱偏压的研究成果，取

(32)

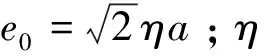
3 结果对比与分析

3.1 轴压承载力验证

由文献[17]可得，式(23)中k为侧压力系数，与混凝土的侧向压力和混凝土本身的强度有关，当混凝土强度一定时，k值随侧压力的增大而减小，当侧压力一定时，k值随混凝土的强度增大而增大，具体可由试验测得，一般取k=1.5～7。本文基于文献[7]与文献[10]十形钢管混凝土短柱轴压与偏压承载力试验研究成果，当k=6.5时，将文献[10]中试验构件参数代入式(30)中，所得轴压承载力计算结果与试验结果对比见表1。对比结果表明，本文的计算结果与试验结果吻合良好，试验结果与理论计算结果比值的平均值为1.032，且最大误差不超过12 %，误差较小。说明依照本文的方法对带约束拉杆十形钢管混凝土柱截面进行划分，并将核心混凝土的侧向约束等效为均匀侧压力，基于统一强度理论分别计算各部分的承载力，最终叠加得到该柱轴压承载力是可行的。并且，当拉杆的数量为0，即不设拉杆时，试验测试的承载力与本文公式承载力公式计算值误差仍在10 %以内，说明当无约束拉杆时，本文的承载力计算公式仍然适用。

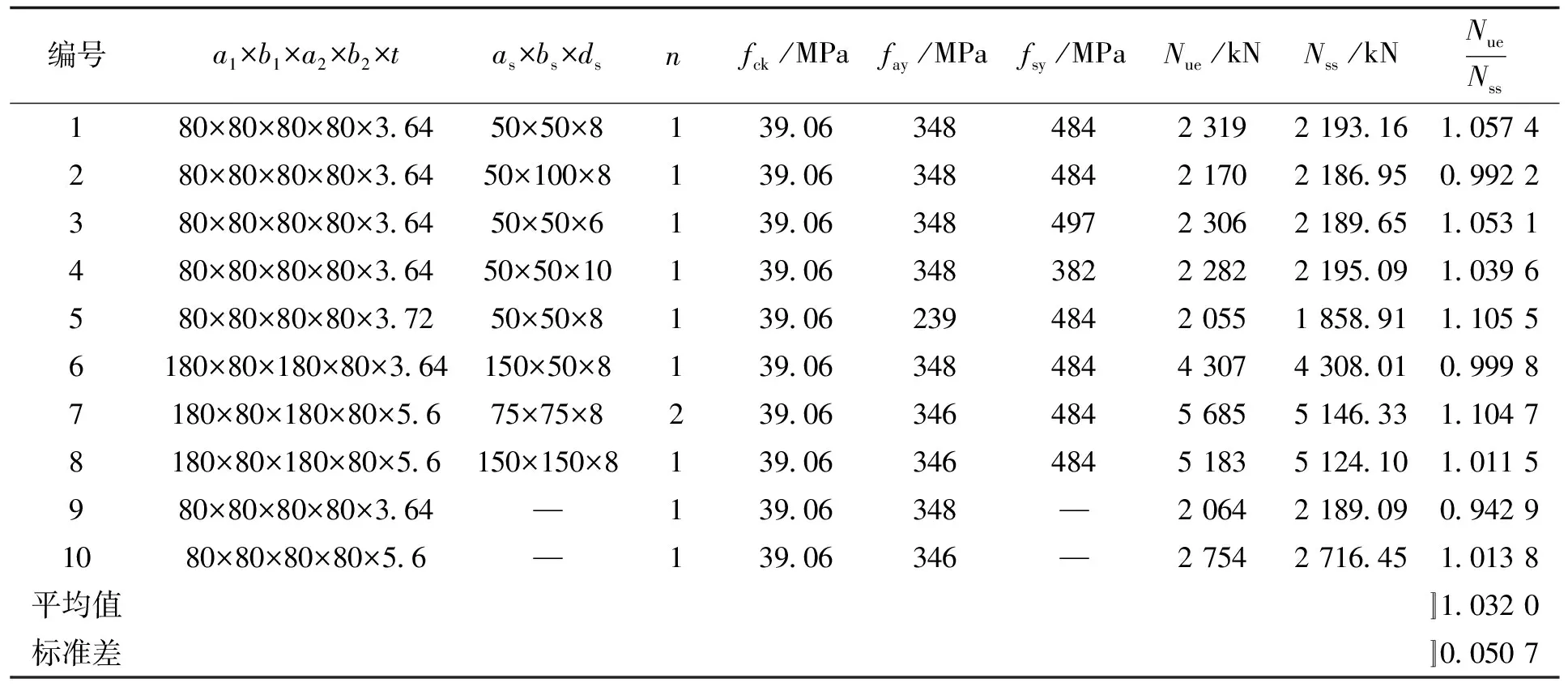
表1 轴压承载力计算值与试验值的比较Tab.1 Comparison between test results and calculated values

注：a1、a2、b1、b2、t均为试件的几何尺寸，见图1；as拉杆最小水平间距；bs为拉杆的最小竖向间距；ds为拉杆直径；n为拉杆列数；表中的长度单位均为mm；fck为混凝土标准轴心抗压强度；fsy为约束拉杆屈服强度；fay为钢板屈服强度；Nue为轴压承载力试验值；Nss为本文轴压承载力计算值。

3.2 偏心受压承载力验证

将文献[7]的试验构件参数代入式(31)中，所得的偏心受压承载力计算结果与试验结果对比见表2。对比结果表明，本文的理论计算结果与试验测得的偏压极限承载力吻合良好，试验结果与理论计算结果比值的平均值为1.0261，且最大误差不超过12 %，误差较小。说明对带约束拉杆十形钢管混凝土柱轴心受压极限承载力进行长细比和偏心率的折减，得到偏心受压极限承载力是可行的，并且说明本文参考文献[19]所得的偏心率和长细比折减系数计算公式对带约束拉杆十形钢管混凝土短柱偏心受压承载力计算具有较好的适用性。

表2 偏心受压承载力计算值与试验值的比较Tab.2 Comparison between test results and calculated values

注：a1、a2、b1、b2、t均为试件的几何尺寸，见图1；as拉杆最小水平间距；bs为拉杆的最小竖向间距；ds为拉杆直径；n为拉杆列数；表中的长度单位均为mm；fck为混凝土标准轴心抗压强度；fsy为约束拉杆屈服强度；fay为钢板屈服强度；θ为荷载角；η为偏心率；Nue为偏心受压承载力试验值；Nss为本文偏心受压承载力计算值。

图6 N与as、bs关系Fig.6 Relationship of N and as or bs

3.3 影响因素分析

3.3.1 拉杆的横向间距和纵向间距

以截面尺寸为a1×a2×b1×b2×t=180 mm×80 mm×180 mm×80 mm×3.64 mm的带约束拉杆十形钢管混凝土轴压短柱为例，当拉杆纵向间距bs分别取50mm、100mm、150mm，拉杆横向间距as以20 mm差值由20 mm递增至120 mm时，柱的承载力变化趋势如图6所示。

由图6可以得出，当拉杆横向间距增大时，轴压承载力下降；对相同的截面形式和横向间距，当竖向间距增大时，钢管混凝土柱的承载力降低。这是因为当拉杆的横向或纵向间距增大时，核心混凝土所受的侧向约束减小，从而使柱的轴向承载力降低。由图还可以得出，拉杆横向间距越小，纵向间距对承载力的影响越大，拉杆横向间距越大，纵向间距对承载力的影响越小。

3.3.2 钢管宽厚比和拉杆直径

以截面尺寸为a1×a2×b1×b2=80 mm×80 mm×80 mm×80 mm，拉杆间距为as×bs=50 mm×50 mm的带约束拉杆十形钢管混凝土轴压短柱为例，当t变化时，会得到不同的宽厚比，以此分析宽厚比R=a2/t(b1/t)对承载力的影响。当宽厚比相同时，取直径相差较大(ds=6 mm、ds=18 mm)的两种拉杆，以此来分析拉杆直径对承载力的影响。

由图7可以看出，当其他构件参数一定时，轴压承载力随钢管宽厚比的增大而下降，这是因为当R增大时，柱的含钢率降低，核心混凝土所受的侧向约束也随之减小，导致柱的整体承载力降低。此外，当构件的截面几何尺寸一定时，承载力随拉杆直径的增加提高不明显。

3.3.3 荷载偏心率

以构件几何尺寸为a1×a2×b1×b2×t×l=180 mm×80 mm×180 mm×80 mm×5.6 mm×1 320 mm，拉杆间距为as×bs=50 mm×50 mm的带约束拉杆十形钢管混凝土偏压短柱为例，当偏心率η由0.1递增至0.35时，柱的承载力变化如图8所示。由图8可以看出，带约束拉杆十形钢管混凝土短柱偏压承载力随偏心率的增大明显降低。

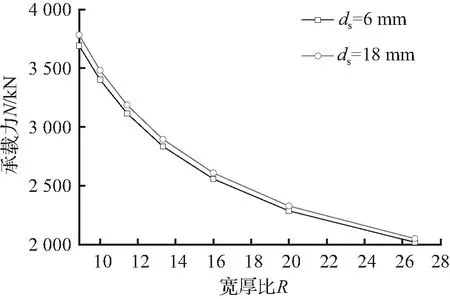
图7N与R、ds的关系
Fig.7RelationshipofNandRords

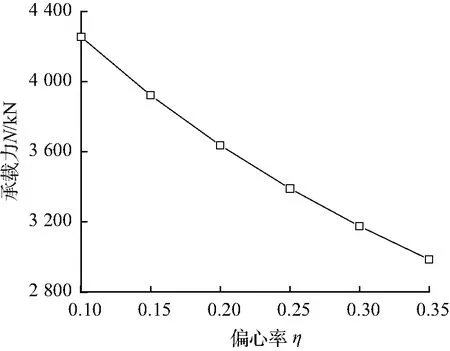
图8N与η的关系
Fig.8RelationshipofNandη

4 结语

① 基于统一强度理论，将带约束拉杆十形钢管混凝土短柱截面划分为5个区域，并对截开面边界条件及核心混凝土强弱约束区合理假设，分析各区域的受力机理，推导出带约束拉杆十形钢管混凝土短柱轴压承载力计算公式，并且在此基础上考虑长细比和偏心率的影响，得到了相应的偏压承载力计算公式。所得公式均有较高的精度且表达简单，具有较好的工程适用性。

② 拉杆间距对柱的承载力有一定的影响。当拉杆间距增大时，承载力降低；当横向间距增大时，纵向间距对承载力的影响减小；柱的承载力随外钢管宽厚比的增大明显降低；荷载偏心率对承载力有较大的影响，当偏心率增大时，柱的承载力明显降低；拉杆直径对承载力影响不明显。

③ 本文计算考虑了中间主应力的影响，k值反映了核心混凝土的内摩擦角，当k的取值不同时，可得到不同精度承载力值。

④ 本文的分析方法同样适用于带约束拉杆T形、L形钢管混凝土短柱，因此为带约束拉杆异形钢管混凝土短柱的承载力计算提供了借鉴。