几种植被覆盖变化趋势分析方法对比研究

王佃来，宿爱霞，刘文萍

(1.首钢工学院，北京 100144；2.中国软件评测中心，北京 100048；3.北京林业大学信息学院，北京 100083)

植被是陆地生态系统的主体，一定程度上能代表土地覆盖变化，在全球气候变化研究中起着指示器的作用[1]。植被动态变化监测和评价一直是生态学研究的重要领域和全球变化研究的热点[2]。植被变化趋势分析是植被动态变化研究中的重要一环，其研究方法较多，下面列举近几年文献中应用的几种主要方法：一元线性回归法趋势分析法[3-13]、相关系数法[14]、Mann Kendall法[8，15]、 Sen Slope Estimator法[2，15]和Sen + Mann Kendall法[2，16-17]。

Spearman相关系数可度量变量之间强弱关系，该系数对数据分布无要求、可发现线性和非线性关系且对异常值不敏感，该研究对该方法在植被趋势分析中的应用进行尝试，并给出应用实例和与其他方法的对比。

为了促进植被变化趋势分析算法在该研究领域的应用和发展，该研究将几种常用的趋势分析方法从植被趋势变化程度分类、方法归类和计算复杂度等方面进行对比和分析。基于北京地区1998—2013年SPOT VEGETATION NDVI数据应用上述几种方法进行植被变化趋势分析，并对试验结果进行对比和分析，以期为该领域的应用研究提供借鉴和参考。

1 几种长时序植被趋势分析方法

1.1线性回归分析法回归分析是研究多个变量之间统计联系的一种重要方法，是分析植被长时序变化趋势的重要方法。基于时间变量x与NDVI因变量y，可使用如下数学模型描述：

y=kxi+εi+a

(1)

式中a,k是未知参数，εi是随机误差。利用观测值(xi,yi)(i=1,2,…,n)可以求出未知参数k。

(2)

(3)

对于NDVI长时序数据，采用最小二乘法线性拟合后得到相应的线性方程，方程的斜率k说明像元NDVI值的多年变化趋势。k>0，表明植被活动呈上升趋势；k<0，表明植被活动呈下降趋势。

关于一元线性回归的植被变化趋势变化程度分类主要有3种方法：第1种对基于某种阈值进行分类[5，8，13]；第2种使用F检验进行显著性判断[9，12]；第3种是使用NDVI序列与时间序列求二者的相关系数，并进行显著性检验来决定分类[7，10]。

1.2Pearson相关系数法Pearson相关系数是研究2个变量之间相关性的方法，是研究长时序植被覆盖变化趋势的重要方法，即以NDVI序列(因变量y)和时间序列(自变量x)相关性表达植被变化的趋势，其数学表达式见公式(4)：

(4)

式中,n为时间序列的长度，rp是自变量x与因变量y之间相关程度度量指标，自变量x代表时间值(年度)，y代表NDVI值。rp>0表示正相关，说明植被呈现增长趋势；rp<0表示负相关，说明植被呈现退化趋势。

rp统计显著检验，在显著水平α下(如：α=0.05)，如果rp大于临界值r,则认为自变量x与因变量y之间显著相关，临界值r可通过查相关系数显著性检验表得到，其自由度为n-2。

在实际应用中可以结合相关显著性检验对植被变化趋势程度进行分类：①rp>0，且rp在显著水平α下显著，表明植被变化趋势为明显改善。②rp>0，且rp在显著水平α下不显著，表明植被变化趋势为轻微改善。③rp<0,且rp在显著水平α下显著，则表明植被变化趋势为严重退化。④rp<0，且rp在显著水平α下不显著，则表明植被变化趋势为轻微退化。⑤如果rp接近于0，则认为植被变化无增加或降低趋势。

1.3Mann-Kendall趋势分析法Mann-Kendall趋势检验过程如下：对于时间序列Xt=(x1,x2,…,xn),Mann-Kendall检验统计量S的计算公式如下：

(5)

式中，n为数据序列长度，sgn(xj-xi)为符号函数，其计算方法如下：

(6)

根据样本数量的不同,显著性检验有所不同，当n>10时，计算标准正态分布统计量Zs,其计算公式如下：

(7)

式中,Var(S)计算公式如下：

(8)

(9)

如果Qmed>0表明植被活动呈上升趋势，Qmed<0则植被活动呈下降趋势。可以结合时间序列的趋势度置信区间进行显著性检验来决定植被变化趋势是否显著。具体计算过程如下：

1.5Sen+Mann-Kendall方法将Sen slope estimator方法中的趋势度与Mann-Kendal方法中的趋势度检验结合，可以形成一种新的长时序趋势分析方法，该方法已成为判断长时序数据趋势的重要方法[13]。其中，趋势度计算方法见公式(9)，趋势度检验量计算方法见公式(8)，在指定的显著水平α下，采用双边检验，即可以判断长时序植被变化趋势。

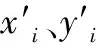
(10)

式中，n为时间序列的长度。

对rs的显著性检验分为以下2种情况：

(1)当样本数n>50时，rs的显著性检验可用t检验，检验统计量见公式(3)：

(11)

式中，n为样本数量，rs为Spearman等级系数。以|t|与由t值表上所查得的自由度为n-2的临界值t′在相应的显著水平α比较决定是否显著。

(2)当样本数n≤50时，rs的显著性检验可以通过查Spearman秩相关系数临界值表判断是否显著。其中自由度为n-2。

2 几种方法对比与评述

2.1方法归类与对比从参数检验和非参数检验的角度来说，上述6种方法可分为2类，其中一元线性回归法和相关系数法属于参数检验，Mann Kendall检验、Sen Slope Estimator检验、Spearman相关系数法和Sen + Mann Kendall检验属于非参数检验。

参数检验是针对某个参数做假设，通常会利用到样本的总体特征，对样本和样本误差分布要求符合正态分布，对噪声敏感；非参数检验是针对总体分布性的假设，无需样本的总体分布特征，对样本初始分布无要求。一般情况下，对于能使用参数检验的样本，首选参数检验。需要指出的是当前长时序植被变化趋势中通常数据组长度比较短，一般不超过30组，大多数情况下十几组，该数量属于统计意义上的少数，且在遥感图像中普遍存在噪声，从这种意义上来说，非参数检验更具优势。

一元线性回归法和相关系数法由于计算过程简单，结果容易解释，且有广泛的应用，被认为是植被趋势分析中的最优方法[18-19]。一元线性回归法受数据绝对量值的影响较大，特别是数据中存在显著大于平均值的数据时，对计算结果影响较大。在实际应用中，建议对数据进行归一化处理，减少极值对计算结果的影响。相关系数是一个没有量纲的归一化系数，不受数据绝对量值影响，可直接度量植被变化趋势而不受NDVI值的影响。

Mann Kendall方法、Sen Slope Estimator检验、Spearman相关系数法和Sen + Mann Kendall法属于非参数检验范畴，通过分析计算公式(6)～(10)可看出，Sen Slope Estimator检验和Sen + Mann Kendall法受数据绝对量值的影响，而另外2种方法是基于比较大小的方法，因此，不受数据绝对量值的影响。在抗噪声方面Sen Slope Estimator检验和Sen + Mann Kendall检验强于Mann Kendall和Spearman相关系数检验法。

2.2方法的植被变化程度分类对比文献中对植被趋势变化程度的分类不尽相同，朴世龙等[14]使用相关系统法结合统计检验方法分类4个等级(显著减小、减小但不显著、增加但不显著和显著增加)；元志辉等[10]使用线性回归法和F检验将植被变化趋势分为5个等级：极显著减少、显著减少、变化不显著、显著增加和极显著增加；宋怡等[5]、丘海军等[8]使用一元线性回归法将NDVI序列与时间序列的回归斜率k使用阈值法分为7等级：严重退化、中度退化、轻微退化、基本不变、轻微改善、中度改善和明显改善；李强等[18]使用Mann Kendall方法将Kendallτ使用阈值法分为8类：极显著持续退化、较显著持续退化、显著持续退化、不显著持续退化、不显著持续改善、显著持续改善、较显著持续改善和极显著持续改善；其他等级请查阅相关文献。

一般情况下，对植被变化趋势的等级划分有2种方法：一种是使用阈值对统计量进行细分，该方法对植被变化趋势等级划分更为细致，通常可以划分为7类、8类或更多，另一种是针对一个统计量使用假设检验，判断是否在统计意义上显著，该类方法一般将植被变化趋势划分为4类或5类。虽然使用阈值法可将植被趋势变化等级划分得更加细致，但是阈值的选取需要使用者具备更多经验和进行更多的后期验证，对应用者提出了更高的要求，并且阈值的选取受使用者主观影响因素较大，有一定的局限性，较难给出统计意义上的解释和论证。使用统计检验对植被变化趋势进行等级划分，受主观因素影响少，一般可将植被变化趋势划分为以下5个等级：显著退化、退化但不显著、基本不变、改善但不显著和显著改善。由于实际计算中基本不变的等级数据较少，有部分文献将该类归于改善但不显著中变为4类：显著退化、退化但不显著、改善但不显著和显著改善。通过对比可以发现，虽然使用统计假设检验受人为因素的影响小，可对结果给出合理的解释和科学论证，但是在等级划分的细致性方面存在一定欠缺，无法进行更细致的划分，在一些应用场景下也有一定的局限性。

2.3方法的计算复杂度参数检验的2种方法(一元线性回归、相关系数法)时间复杂度为O(n)，而非参数检验的4种方法Mann Kendall、Sen Slope Estimator、Spearman相关系数、Sen + Mann Kendall时间复杂度均为O(n2)。从计算复杂度上来说一元线性回归和相关系统最为简单，而对于非参数检验的4种方法虽然时间复杂度均为O(n2)，但是在计算复杂度上也差别较大，Mann Kendall 只涉及简单的比较运算；而其余3种方法均需要对数据进行排序，而Spearman相关系数法需要对数据进行2次排序，并且在计算秩次时也比较复杂。如果从计算和实现复杂度对4种非参数检验方法进行从高到低的排序，顺序如下：Spearman相关系数法>Sen + Mann Kendall法>Sen Slope Estimator检验>Mann Kendall检验。一元线性回归和相关系数法大致相当，且计算量明显小于上述4种非参数检验方法。

2.4各方法在北京市植被变化趋势中的应用为了直观地比较上述几种方法之间的差异，基于1998—2013年北京地区SPOT VEGETATION遥感数据应用上述6种方法进行植被趋势分析。

试验结果如图1和表1所示。图1中的图A～F分别是应用一元线性回归法、相关系数、Mann Kendall法、Sen Slope Estimator检验法、Spearman相关系数法和Sen +Mann Kendall法的植被趋势分析结果。植被变化趋势共分为5个等级，分别为显著改善(深绿色)、改善但不显著(浅绿色)、基本不变(黑色)、退化但不显著(浅褐色)和显著退化(褐色)。表1中给出了6种方法在北京地区植被变化趋势等级所占整个北京市总面积的百分比。上述6种方法均采用统计假设检验来验证是否显著变化，其中：一元线性回归法采用F 检验判断变化是否显著(回归斜率k>0且统计量f<0.01，则植被变化趋势为显著改善；k>0且统计量f≥0.01，则植被变化趋势为改善但不显著；k<0且f<0.01，则植被变化趋势为显著退化；k<0且f≥0.01，则植被变化趋势为退化但不显著；k=0则认为植被变化趋势为基本不变)；相关系数、Mann Kendall和Sen+ Mann Kendall均采用显著水平α=0.05的假设检验判断植被变化趋势是否显著；Sen Slope Estimator检验和Spearman检验分别参考该研究1.4和1.6节中的显著性判断方法。

比较图1中的图A～F可发现，图A与其他5幅图在空间分布上有较大差异，特别是在植被显著改善和显著退化区域,图B～F中植被显著改善区域集中在北京市北部，而图A则不同。此外，图B～F中植被显著退化的区域集中在环绕北京市城区的区域，而图A则不同。从以上分析可看出，在北京地区植被趋势变化分析中一元线性回归法与其他5种方法存在较大差异。图B～F的5种植被变化趋势等级分布在空间上存在很高的一致性，特别在植被显著改善和显著退化的区域表现出惊人的一致。

表1 各方法植被趋势分析结果

图1 1998—2013年北京市各方法植被变化趋势Fig.1 Image results of trend analysis of vegetation cover change for each method in Beijing City during 1998-2013

从表1可看出，6种方法在北京市植被变化趋势分析结果中基本不变、退化但不显著和显著退化3个变化等级中较一致，最大差异不超过2%，显著退化区域的最大差异仅有1.41%，有较高的一致性。一元线性回归法与其他5种方法的差异性较大。这一点可从图1中得到直观印证。

在植被变化趋势为显著改善的区域中，除一元线性回归法外，其余5种方法的检测结果主要集中在北京市的北部(图1)。从表1可知，一元线性回归法在植被显著改善的区域仅为8.87%，其余5种方法均超过16.00%，存在较大差异。用6种方法分析植被变化趋势发现，植被改善(包括显著改善和改善但不显著)与植被退化(包括显著退化和退化但不显著)的区域均分别在72%与27%左右，差异并不大。因此，一元线性回归法在植被基于F检验进行显著性判断时其检出数据明显小于其余5种方法，其敏感性低于其余5种方法。此外一元线性回归法检出的植被显著改善区域也与其余5种方法的检出区域在空间分布有较大不同。

在植被变化趋势为改善但不显著的区域中，6种方法的检测结果在空间分布较为相似。从数据上来看，一元线性回归最高为64.32%,Spearman相关系数法最低为50.97%，其余4种方法在51%～57%，差异较小。

在植被变化趋势为基本不变的区域中，Sen Slope Estimator方法和Sen+Mann Kendall方法中检出的值最多且相等，导致此结果的原因是如果植被的NDVI序列中存在较多相同值时，由公式(9)可知会存在较多的0值，因此上述2种方法的检测结果出现较多的基本不变区域。此外，Mann Kendall方法中由公式(6)可以看出检验统计量S也存在0值可能，从该方法的检测结果上可看出，约存在0.61%的区域为基本不变区域。一元线性回归法、相关系数法和Spearman相关系数法的检测结果几乎不存在基本不变区域，这一点可通过分析公式(2)、公式(4)和公式(10)得到答案。

在植被变化趋势为退化但不显著的区域中，6种方法的检测结果无论在空间分布上，还是在数据上均一致，数据的最大差异仅为1.84%,该区域主要集中在环北京市城区的区域。

在植被变化趋势为显著退化的区域中，除一元线性回归法外，其余5种方法的检测结果在空间分布和数据上基本相同，象一个马蹄形环绕在北京市城区，仅在西北方有一个开口。

3 结语

(1)参数检验中的一元线性回归法与相关系数法两者计算量相当，对噪声敏感，对数据的分布要求满足正态分布，试验结果对比显示两者的检测结果在空间分布和数值上存在较大差异，相关系数法与非参数检验的4种方法的检测结果较一致。在噪声和数据分布相同条件下的植被趋势变化分析中，植被变化趋势等级划分粒度较粗时，推荐使用相关系数法；如果要对植被变化趋势等级进行细致划分，则使用一元线性回归法选择合适的阈值区间划分植被变化趋势等级。

(2)非参数检验的4种方法在植被趋势变化检测的结果中显示在空间分布和数值上基本一致，如果数据质量较高且噪声较少时，推荐使用Mann Kendall法；如果数据中存在较多噪声，则推荐使用Sen + Mann Kendall法。Spearman等级相关系数法对数据分布无要求、可发现线性及非线性关系和对异常值不敏感的特性，可作为一种有潜力的植被趋势方法使用。

(3)在长时序遥感植被变化趋势分析中，受遥感数据集的限制，数据组的长度往往小于30，并且遥感数据集中普遍存在噪声，非参数检验是一种较好的选择。今后将选择更多的数据集和区域进行结果验证，进一步分析上述方法的优劣，为植被变化趋势分析研究提供借鉴和参考。