旬阳水电站导流明渠渠首进口形式数值模拟研究
2019-03-18尹进步张曙光赵东阳刘志明
杨 彦,尹进步,张曙光,赵东阳,刘志明
(西北农林科技大学水利与建筑工程学院,陕西 杨凌712100)
0 引 言
导流明渠作为一种常见的导流方式,以其泄流能力强、易满足通航要求等优势,在许多大、中型水利水电工程中被广泛应用,但导流过程中常会出现导墙墩头绕流严重、渠内流态不稳定、过流能力不足等问题。研究表明,导流明渠进口形式是影响导流明渠水力特性及渠首部位冲刷的主要因素之一,因此需要对此进行深入研究。通过模型试验对导流明渠进口形式的研究资料比较多,刘宁[1]对三峡大坝左导墙长度进行研究,发现缩短导墙长度可以改善水流流态,减轻河道冲刷。王均星等[2]通过物理模型试验,研究了宽浅导流明渠渠首位置进口形式对明渠泄流能力及明渠内部水流特性的影响。郭观明等[3]探究了不同布置形式的溢流坝进水口导墙对工程运行的影响。随着计算机技术的发展,数值模拟也成为一种重要的研究手段,刘晓平等[4]对某低水头电站导墙进行三维数值模拟,研究了导墙长度与电站进水口前流态的关系。周茂林等[5]通过对桐子林水电站明渠弯道流场进行三维数值模拟,获得了详细的流场信息,可为体形优化提供参考。
旬阳水电站洪水期峰高量大,陡涨陡落,使得导流明渠面临着巨大泄流压力;模型试验观测发现:在上游围堰导向作用下,上游来流在导墙上延段墩头部位存在绕流、两侧水位落差大、基础冲刷严重等问题,本文采用RNGk-ε模型结合自由液面追踪的VOF方法,对旬阳水电站导流明渠进行三维数值模拟,得到了渠道内水面线、流速场分布等水力特性参数,并依此对导流明渠进口形式进行了优化研究,得到较优的进口段推荐形式,为工程实践提供一定参考。
1 数值模拟研究
1.1 控制方程
控制方程是质量守恒定律、动量守恒定律、能量守恒定律等守恒定律的数学描述,其具体表达式如下。
连续性方程:
(1)
动量方程:
(2)
式中:ρ为体积分数加权平均的密度;μ为体积分数加权平均的分子黏性系数;p为修正压强;μt为紊流黏性系数;Cμ为经验常数,本文取Cμ=0.048 5;μt+μ为广义黏性系数;ui、uj分别为流速矢量在方向xi、xj的分量。
1.2 湍流模型
RNGk-ε模型是基于重正化群(Renormalization Group)的理论提出来的。在RNGk-ε模型中,通过在大尺度运动和修正后的黏度项体现小尺度的影响,而使这些小尺度运动有系统地从控制方程中去除,可更好地模拟强逆压梯度流、分离流动、边界层流动、旋转流动等[6]。RNGk-ε模型的湍动能k和湍动能耗散率ε方程如下。
湍动能k方程:
(3)
湍动能耗散率ε方程:
(4)
式中:k为湍动能;ε为湍动能耗散率;Gk、Gb分别是由平均速度梯度和浮力引起的湍动能产生项;YM代表脉动扩张的贡献;C1ε、C2ε为经验常数,取1.44、1.92;σk、σε分别是与湍动能k和耗散率ε对应的Prandtl数,取1.0、1.3。
1.3 VOF方法
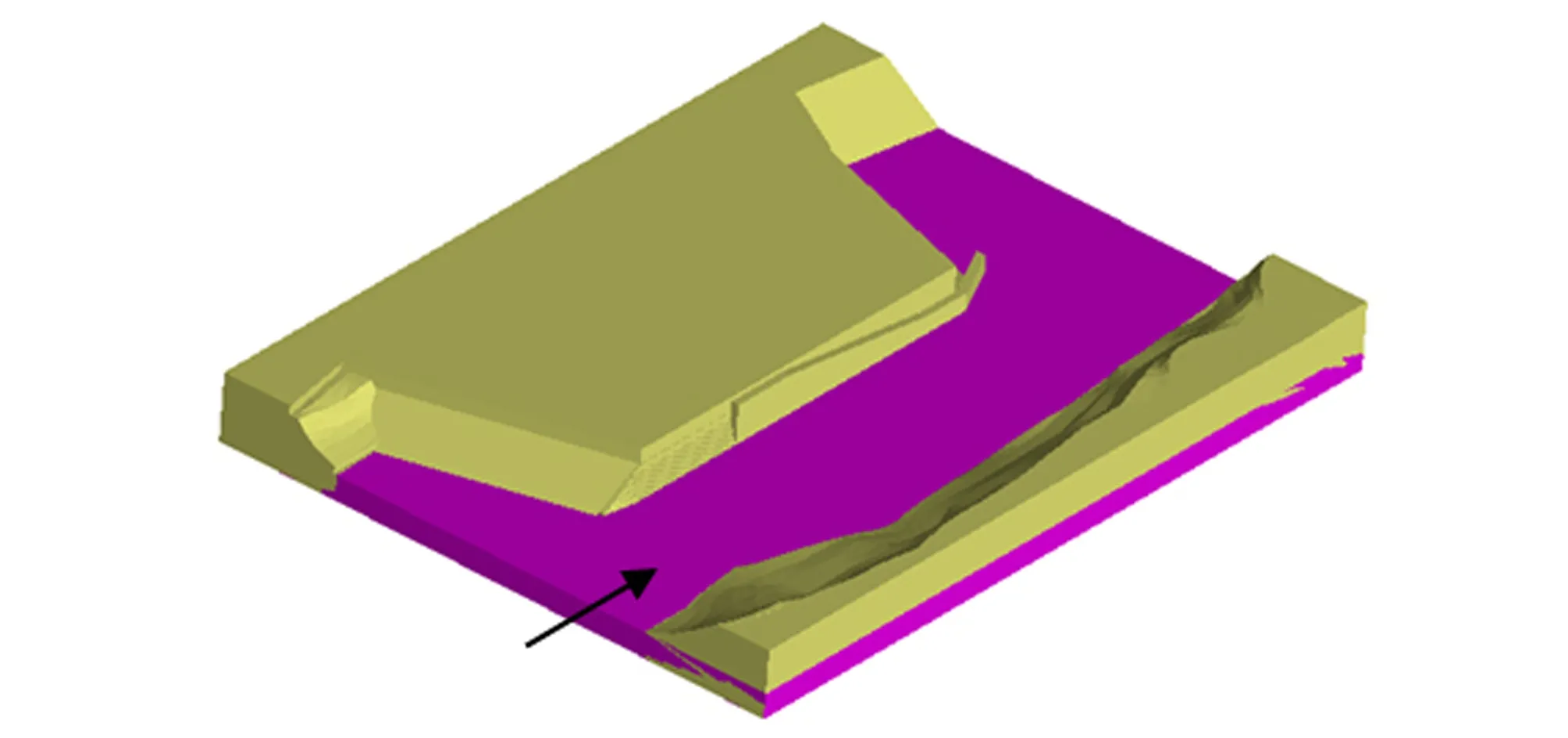
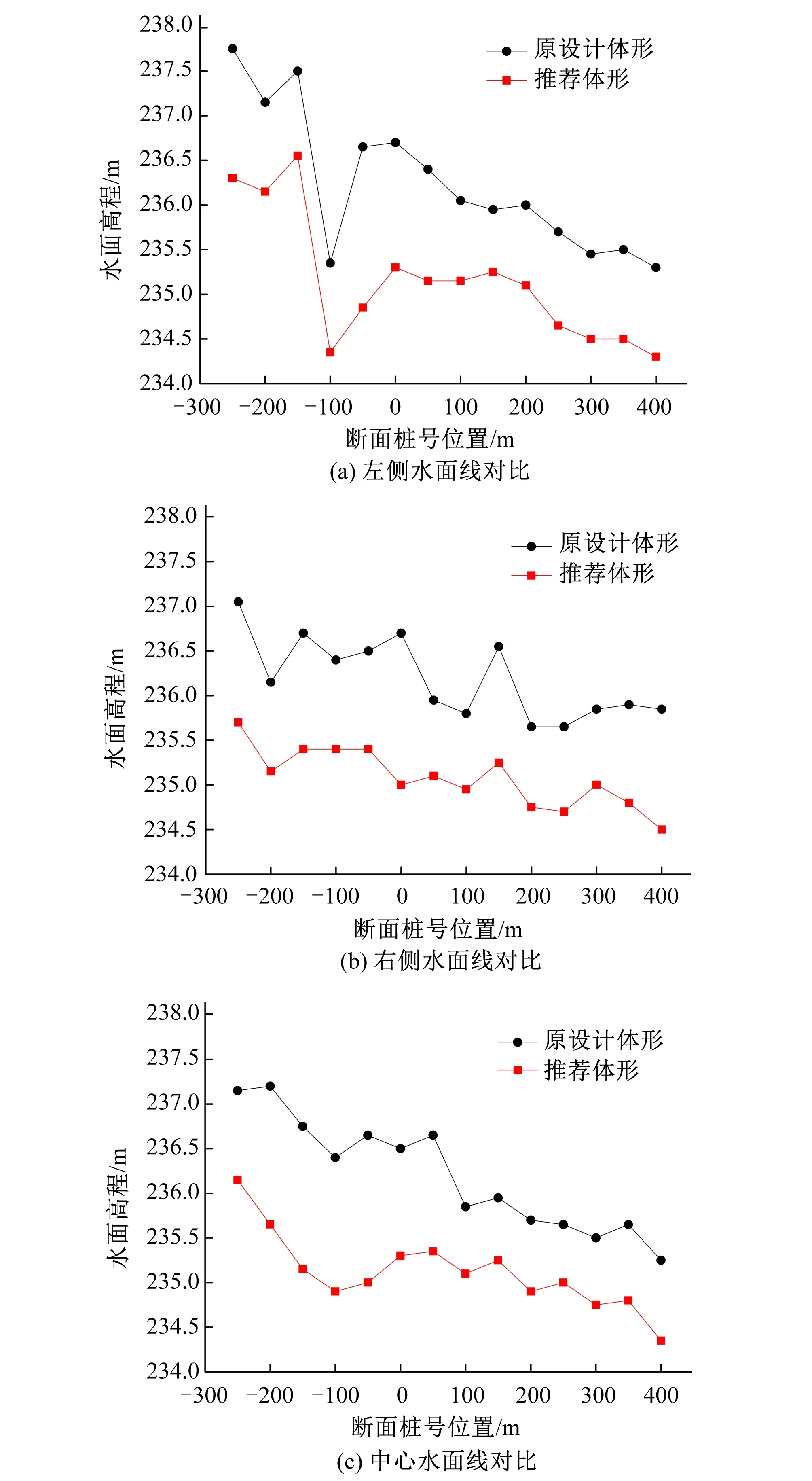
采用VOF法对自由表面进行追踪,其基本原理是通过研究网格单元中流体和网格体积比函数F=F(x,y,z,t)来确定自由面,追踪流体的变化。在计算过程中,一个控制体将会出现以下3种情况:当F=0时,表示控制体内充满空气;当F=1时,表示控制体内充满水;当0 (5) 式中:VF表示流动的体积分数;Ax、Ay、Az分别表示x、y、z可流动的面积分数;u、v、w表示3个方向的流速。 根据原有设计资料,在CAD中按原型1∶1建立三维模型,将生成模型实体导入flow-3d中,激活湍流模型、重力模型。模拟计算区域从坝上250 m到坝下400 m,包括导流明渠进口段、导流明渠段和导流明渠出口段及河道地形等部分,计算工况为20 a一遇洪水(P=5%),流量为19 500 m3/s;定义坝上250 m断面、右岸地形与底板底面的交点为计算区域的坐标原点,x轴指向河道的下游,y轴与水流运动方向垂直,z轴垂直向上。 计算采用结构化网格,为减小多块网格连接处的水力计算损失,整个计算采用一个网格块,网格尺寸为1.4 m×1.4 m×1.4 m,总网格大小约55 万个。具体计算区域和网格划分见图1,压力求解器选用广义极小残差算法(GMRES)、基于压力隐式求解法( Implicit)。计算结果数据输出间隔为60 s,输出数据有流速、压力、水的体积分数、自由液面高程等[7,8]。 图1 导流明渠网格划分Fig.1 Grid division of diversion channel 上下游均为压力边界P,流体体积分数为 1,水位分别为237.32 m(导流明渠底板以上水深23.32 m)和235.47 m(导流明渠底板以上水深21.47 m);模型底部设为无滑移固壁边界W;与空气接触的顶面设为体积分数为0的压力边界P;其余边界采用对称边界S。本次模拟在初始时刻将上下游河道填充与出口边界条件水位一致的静止水体,将静水压强方向设置为沿重力方向线性变化。 为了分析计算结果的合理性,首先将计算结果与模型试验值进行对比,模型试验在旬阳水电站1∶80整体模型上进行,数值模拟采用flow-3d软件。计算与模型试验均选择典型工况20 a一遇洪水进行,以下从水流流态、水面线、流速对2者进行对比验证。 原设计体形数值模拟与模型试验流态对比见图2。通过对计算结果分析发现,上游河道来流基本沿原主河槽下泄,当水流行至墩头前10 m范围内时,受围堰导向和导流明渠位置影响,水流主流流向总体向右岸偏转,墩头部位由于受到前伸墩头影响,水流在墩头附近形成一个绕流区域,进入导流明渠后,主流仍偏向右岸,并在导墙右侧形成一定范围的回流区,回流区横向宽度大约占据明渠1/3,导流明渠主流到达坝下0+050 m断面附近,受到右岸边界导向,又逐渐向左岸扩散,导墙右侧回流旋转强度也逐渐减弱,最终消失于导墙末端,与模型试验观测流态基本吻合。 图2 模型试验与数值模拟流态对比Fig.2 Comparison of flow field between model test and numerical simulation 水面线作为围堰和导墙高度的设计依据,在模型试验测试中也是重点量测的参数之一。图3为各断面水面线计算值与试验值对比图。由图3可知:①在明渠进口前,受过流断面收缩影响,水面相对明渠水面比较高,但试验值比计算值略低一些;②)在进口段,受墩头绕流与离心力作用,墩头附近水面出现跌落,计算与试验测量结果基本相同;③明渠段水面计算值与试验值基本吻合;④在出口段水面线变化趋势一致,但计算略大一些。各断面的计算误差见表1,相对误差在1%以内,最大绝对误差为0.47 m。对水面线计算结果的总体分析发现,模型试验明渠进口前与出口段河床出现局部冲刷,而数值模拟采用刚性底板,因此计算结果略高一点,但计算水面线总体趋势与试验结果基本符合。 图3 模型试验与数值模拟水面线对比Fig.3 Comparison of water surface profiles between model test and numerical simulation 断面桩号位置/m试验值/m计算值/m绝对误差/m相对误差/%-250237.32 237.30 -0.02 -0.01 -150236.98 237.28 0.30 0.13 -50236.60 236.45 -0.15 -0.06 50236.33 235.86 -0.47 -0.20 150236.15 236.38 0.23 0.10 250235.67 236.00 0.33 0.14 350235.68 235.98 0.30 0.13 图4为各断面数值模拟计算的平均流速与模型试验测量值对比图。从中可以看到,流速沿河道方向,呈现先增加后减小再增加的变化规律,这是由于上游围堰束窄,使过流面积减小,导致流速增大;过了回流区,流速变小;在明渠出口处,过水断面扩宽,水面出现跌落,水深急剧减小,流速再次增加。明渠进口前模型试验测出的流速值与计算值均为4~5 m/s,差值为0.35~0.68 m/s,明渠内流速值为4~7 m/s,差值为0.18~0.47 m/s。各断面平均流速相对误差基本在10%以内,最大绝对误差为0.68 m/s,2者流速分布一致。总体说来,水流各个断面模型试验测量值分散在计算断面流速曲线附近,且2者差值不大,这表明计算值与试验值比较吻合。 图4 模型试验与数值模拟流速对比Fig.4 Comparison of flow velocity between model test and numerical simulation 由数值模拟与模型试验的对比结果可知:数值模拟流态与模型试验流态基本吻合,数值模拟计算水面线与模型试验实测水面线总体趋势一致,误差较小,数值模拟流速分布与模型试验流速分布基本一致,差值也比较小。由此可见,数值模拟计算是合理的,可以应用于该明渠水力特性计算分析中。 通过模型试验和数值模拟计算发现:原设计体形存在进口流态紊乱现象,而且纵向导墙墩头绕流严重,墩头前出现较大冲刷坑,导墙附近临底流速也比较大,对导墙基础产生一定淘刷,受绕流影响,明渠内有大面积回流,导致明渠过流能力减小。针对以上问题最后确定的原设计体形优化原则为:①尽可能减小墩头前绕流,改善明渠进口水流流态;②尽可能使冲刷位置远离建筑物,减小冲刷坑深度。对比不同方案,最终采用的推荐体形为:在原设计体形基础上,将导墙上延段缩短10 m,同时把上游围堰原折线式轴线修改为直线形式,见图5。对推荐体形进行数值模拟计算,并将计算水流流态、水面线、冲刷等参数分布规律与原设计体形进行对比分析,分析结果如下。 图5 推荐体形三维图Fig.5 Recommended shape of three-dimensional 图6为原设计体形与推荐体形流态对比图,从图6中可以看出,2种体形水流流态基本相似,在上游围堰前和下游围堰后均能形成回流区,导墙右侧水流紊乱,且存在一定范围的回流区域,回流区内伴有旋涡。原设计体形水流从上游河道进入明渠前分成2部分,一部分沿着主河槽继续下泄,另一部分水流受上游围堰阻挡,在围堰前产生横向流动,靠近纵向围堰后又受到导墙影响,墩头水流出现明显绕流凹陷,水流绕过导墙后出现较为剧烈的翻滚、涌浪等不良流态,且伴有大范围的回流区域。推荐体形水流从河道进入明渠时也分成2部分,一部分沿着主河槽继续下泄,但受上游围堰阻挡的另一部分水流顺着围堰直接进入主河槽,2部分水流在明渠进口相汇,墩头附近几乎不出现较大绕流现象,致使导墙右侧区域流态有明显改善,虽然还有回流产生,但比起原设计体形回流范围缩小近1/2,导流明渠过流能力明显增加。由此说明,推荐体形无论局部流态还是整体流态都要优于原设计体形。 图6 原设计体形与推荐体形流态对比Fig.6 Comparison of flow field between the original design and recommended shape 采用自由液面追踪的VOF法可准确描述出自由液面变化情况。由计算结果可知:2种体形上游河道水面均较平稳、比降较小,水面无明显跌落现象,左右岸水位差值较小,水流进入导流明渠后水面产生一定跌落,特别是坝上0+100 m断面处,过了绕流区后水面逐渐趋于平稳。为了能反映出2种体形水面线的差异,计算结果提取3组水面线值,依次为左侧水面线、中心水面线和右侧水面线。图7为原设计体形与推荐体形各水面线对比图。从图7中可以看出:2种体形水面线变化趋势大致相同,但推荐体形水面波动明显要小于原设计体形,而且推荐体形水面线高度有了一定幅度的降低,左侧在坝上0+100 m~坝下0+050 m下降的范围为1.0~1.8 m,中线在坝上0+250 m~坝下0+50 m下降的范围为1.00~1.65 m,右侧在坝上0+250 m~坝下0+000 m下降的范围为1.0~1.7 m,水面线高度总体下降幅度都比较大,特别是左侧水面线下降,可以使纵向围堰高程降低。从水位的具体数值分析可知:原设计体形围堰前水位比上游围堰顶部高程239 m低1.0 m,推荐体形低2.3 m,原设计体形下游水位比下游围堰堰顶高程236 m低0.5 m,推荐体形低1.2 m,原设计体形导墙坝下0+139 m~坝下0+182 m水面基本在235~236 m之间,推荐体形均低于235.5 m。上述对比结果表明:相同工况下,推荐体形可适当降低围堰高度,减小工程量。 图7 原设计体形与推荐体形水面线对比Fig.7 Comparison of water surface profiles between the original design and recommended shape 图8为原设计体形和推荐体形水平流速矢量图。从计算结果可知:原设计体形上游来流流速较小,大致为4~5 m/s,沿水深方向流速呈对数分布,最大流速为5.08 m/s,出现在坝上0+200 m断面,当水流流经围堰时,出现壅水,使其局部区域内流速减小,但围堰前流速仍大于围堰的抗冲流速3 m/s,随着河道束窄,流速逐渐增大,在墩头附近出现极大值,达6.8 m/s左右。由于推荐体形缩短导墙长度和拉直上游围堰后,绕流强度减小,使围堰前流速也有所减小,最大值仅仅接近围堰的抗冲流速,水流顺着围堰直接从导墙墩头右侧流入明渠内,随着明渠内流态得到改善,其表面流速和底面流速均低于原设计体形,尤其是位于回流边界上的流速从原设计体形的4~6 m/s降低到2~5 m/s,墩头附近的流速从6.8 m/s下降到5.79 m/s。图9为原设计体形和推荐体形临底流速分布图。从图9中可以看出,原设计体形3个位置的临底流速分布差别不大,3组流速值交替变换,明渠内的流速大致为5~6 m/s,流速呈现出均匀变化的规律;而推荐体形3组流速值变化比较明显,中间流速大,两边流速小,特别是左侧边界流速最小,只有2~5 m/s,右侧流速略大一些,为4~6 m/s,中心线上的流速分布范围与右侧流速基本相同。综合比较可知,推荐体形临底流速普遍略小于原设计体形,左侧更小一些,均对右导墙稳定比较有利。 流态和临底流速的变化影响着冲刷的演变和发展,流态紊乱,临底流速大,相应的冲刷就会严重,基于流场特性和模型试验实测冲刷图分析,可以大致判断出导流明渠渠首冲刷情况。模型试验冲刷料根据抗冲流速按伊兹巴什公式进行计算选取,经计算,覆盖层选取粒径为1~2 mm的冲刷料(抗冲流速为1~2 m/s),基岩选取5~8 mm的冲刷料(抗冲流速为3.5~4.5 m/s)。图10(a)为原设计体形冲刷图。从图10(a)中可以看出,原设计体形在右导墙墩头周围形成一较大冲刷坑,冲坑最深点高程已达190 m,冲刷料堆积在明渠内坝下0+100 m断面处靠近导墙处,堆积体最大高程为218 m。这是由于进口形式不合理,导致墩头周围临底流速值基本在4.5 m/s以上,最大值达到6.8 m/s左右,远大于河床基岩的抗冲流速,加之导墙和围堰的共同作用,被围堰拦截的水流被迫从导墙墩头绕流,一方面使得导墙墩头周围的单宽流量增加,另一方面使得墩头左右两侧产生水头差,该部分水体拥有更多的位能,向动能形式转化主要发生在导墙墩头处,表现为水流在短距离内极速下潜,导致墩头周围形成较大冲刷。图10(b)为推荐体形冲刷图。由图10(b)可知,冲刷坑位于导墙右侧,冲坑最深点高程为203 m,冲刷料堆积在0+000 m断面处,明渠出口处有部分冲刷,冲坑最深点为206 m。分析其原因,拉直上游围堰,水流顺着围堰直接进入明渠,导致墩头附近几乎不出现绕流,其周围的临底流速为3~4 m/s,大致和基岩的抗冲流速相当,几乎不会产生冲刷,2部分水流在导墙墩头右侧发生碰撞,导致墩头右侧水流动能降低,临底流速减小,冲刷减弱,冲坑位置由墩头转移到导墙右侧。由此可见,推荐体形不但可以降低导流明渠的左岸临底流速,而且可以改变导墙墩头的冲刷坑位置,最大限度地减小墩头及导墙的冲刷,对导墙稳定比较有利。 图10 原设计体形与推荐体形冲刷对比Fig.10 comparison of scour between original design and recommended shape 通过对比原设计体形与推荐体形的流态、水面线、流速、冲刷可以看出,缩短导墙长度和拉直上游围堰可以减小回流区面积,增加导流明渠过流能力,改善明渠内水流流态。由于导流明渠内水流变得平稳后,水面线高度下降,从而可以降低围堰和导墙的高度,减少工程量。深入分析还发现:墩头部位的绕流强度和范围显著减小,墩头部位的水流跌落降低,进口部位的冲刷状况得到改善,冲刷位置远离建筑物,深度减小。推荐体形的各种水力参数指标均优于原设计体形。 本文应用flow-3d软件对旬阳水电站一期导流明渠水流特性进行了三维数值模拟,主要得出以下结论。 (1)通过对比数值模拟和模型试验得到的流态、水面线和流速可知,数值模拟结果和模型试验结果基本吻合,即该计算方法可应用于导流明渠计算和优化研究。 (2)相比于原设计体形,推荐体形缩短导墙长度和拉直上游围堰各项指标都比较好,缩短导墙长度能改善明渠内水流流态,减轻进口段的冲刷,拉直上游围堰能减小墩头部位的绕流,降低两侧的水位差,使冲刷坑的位置远离建筑物。1.4 模型建立与网格划分

1.5 边界条件
2 计算与试验验证
2.1 水流流态对比

2.2 水面线对比
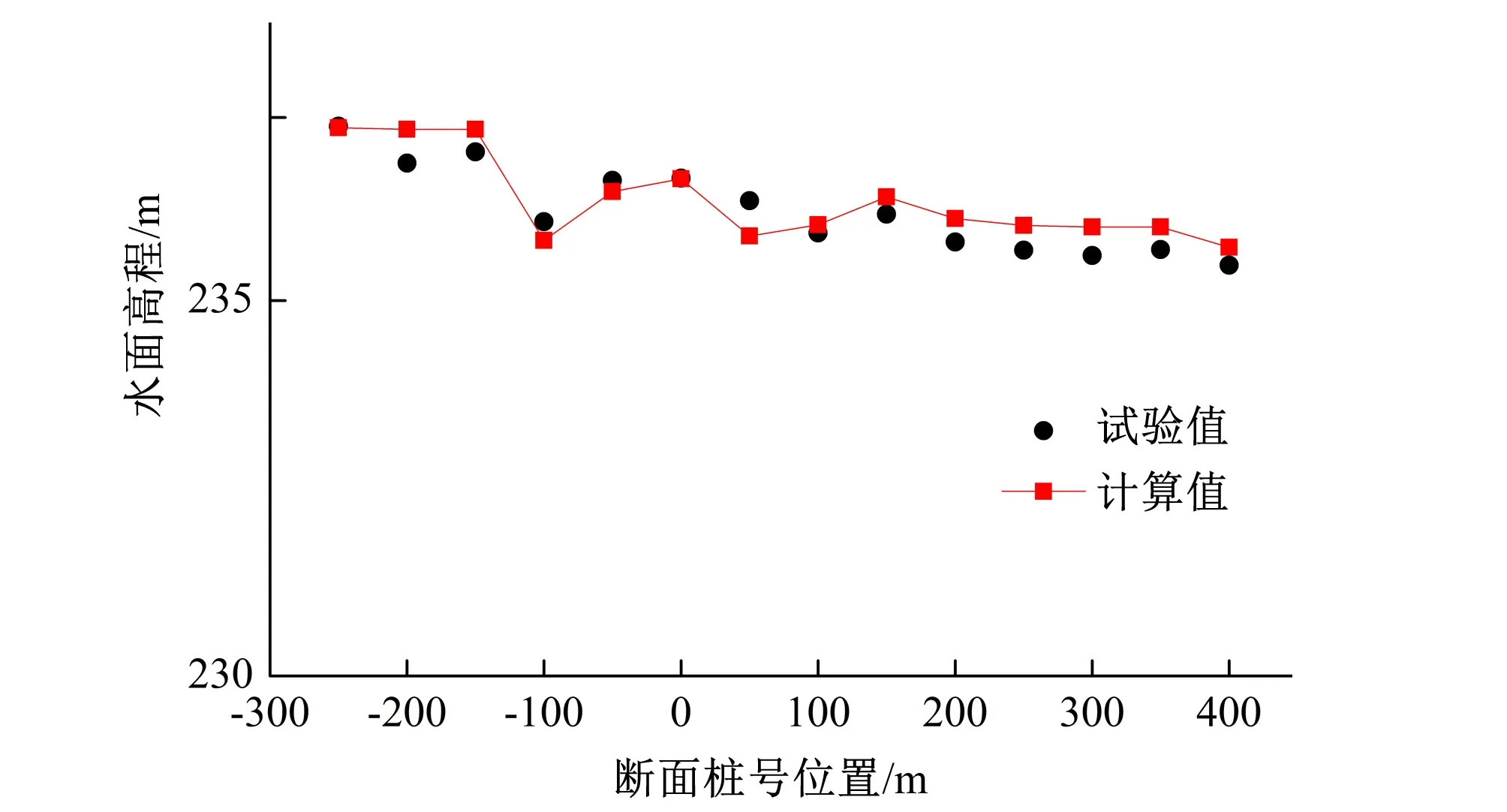
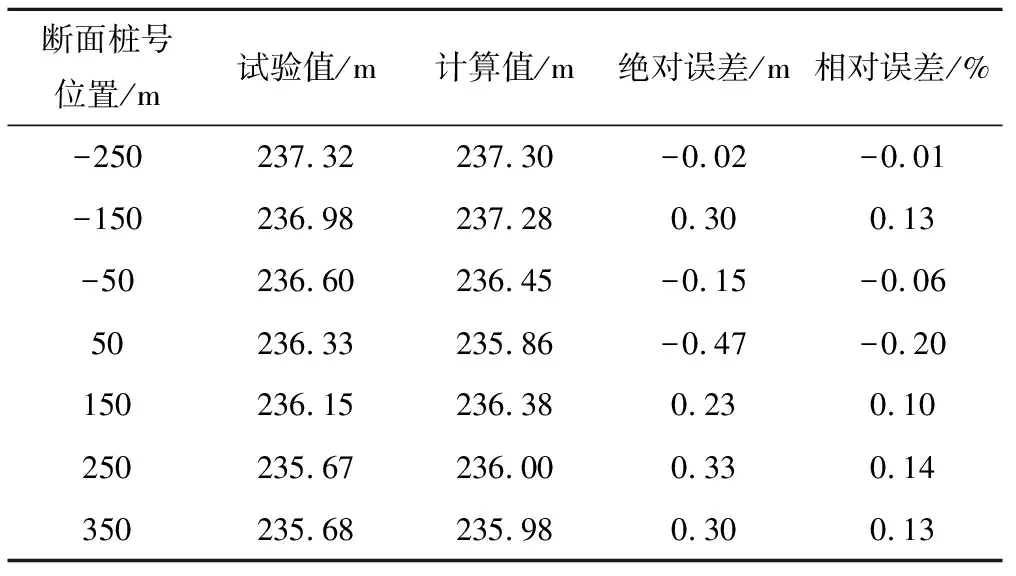
2.3 流速对比
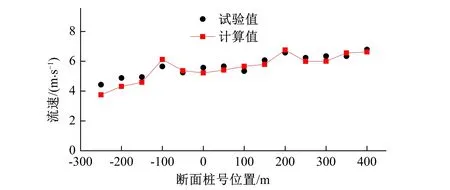
2.4 对比结果小结
3 进口体形优化研究
3.1 流态分析
3.2 水面线分析
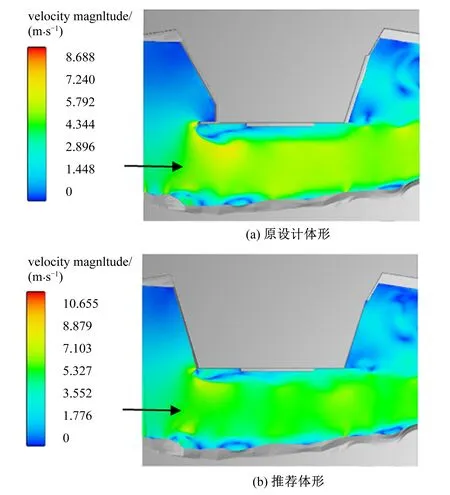
3.3 流速分析
3.4 冲刷分析
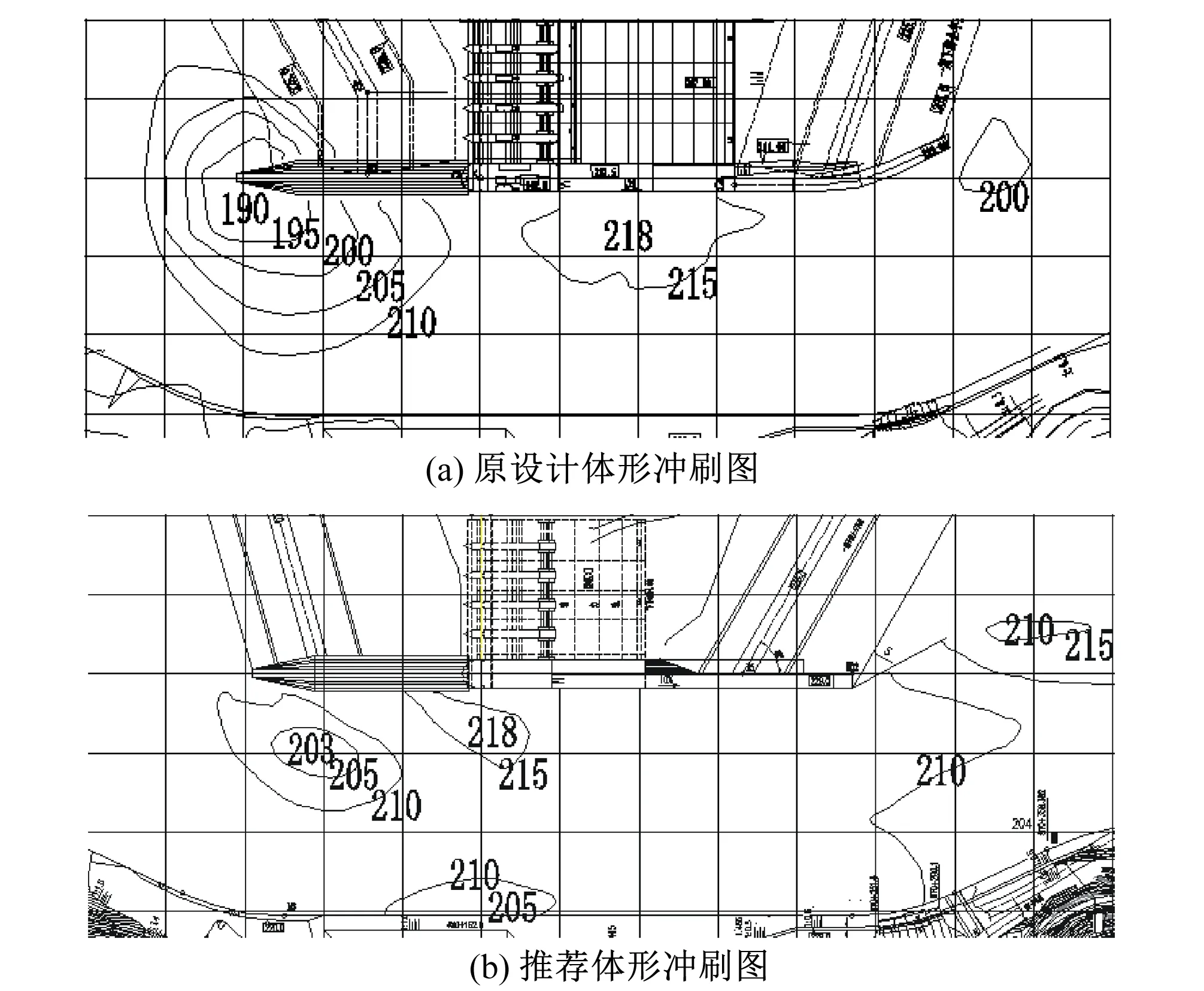
3.5 小 结
4 结 论
