基于Markov链的施工度汛应急资源动态调度研究

韩 凯，彭 辉，罗兆英

(三峡大学水利与环境学院，湖北 宜昌 443002)

0 引 言

施工度汛是水利水电工程建设过程的关键环节之一。施工度汛一旦失事不仅使部分已建工程冲坏而前功尽弃，而且将导致推迟发电，同时也会给下游的工农业生产和居民的安全带来威胁。根据国内外有关资料可知，大坝度汛失事主要是因为遭遇超标准洪水的袭击或库区大滑坡产生较大涌浪的冲击[1]。科学的规划调度有限的应急资源，不仅是施工度汛应急预案的重要内容[2]，同样也是保证施工人员安全及施工进度的关键。

水利水电工程施工度汛风险具有发生的不确定性、发生过程的随机性、规模大等特点[3]。多年来，国内外学者对施工度汛及资源调度进行了诸多研究：谢小平等[4]对龙羊峡水库不同运行方式下公伯峡水电站的施工度汛方案，采用概率分布函数进行风险分析。根据高堆石坝填筑施工过程的挡水和过水的特点，刘潋等[5]以坝体挡水高程的时变性和坝前水位的随机性描述施工度汛风险。张超等[6]基于水动力学理论，建立了上游水电站围堰漫顶溃决条件下中期度汛水位变化过程模拟的数学模型。晋良海等[7]采用分割多目标风险法(PMRM)给定分割概率,得到多种风险函数并加入到风险决策模型的目标函数中进行风险决策。RAWLS等[8]在不确定是否发生自然灾害的情况下，确定要预先定位的各种应急物资的位置和数量，进而提出了一个两阶段随机混合整数规划。GANG K等[9]提出了一种“情景反应”型灾后应急物资供应方案。为减少水电站大坝群安全应急管理中的资源浪费，JIANG X等[10]提出了一种水库大坝群应急管理协同测量方法。

综上，目前国内外对施工度汛风险的研究较为集中，而如何在有限的施工度汛应急资源约束下，考虑施工度汛的动态变化特征，平衡安全度汛与度汛成本最低，是施工度汛应急资源调度方案选择的难点[11]。除此之外，水利水电施工度汛是一个具有无后效性的连续变化的过程。于是，本文考虑施工过程中度汛风险特征，基于马尔科夫动态决策理论建立资源调度模型，选择安全且经济的资源调度方案。

1 施工度汛与马尔科夫链

1.1 施工度汛特征

施工度汛风险具有独一性、动态演化等一系列特征，据此，施工度汛应急资源的调度决策问题有以下3个主要特征[12]：①施工度汛风险是逐渐演化的，具有很大的动态性和随机性；②施工度汛风险发展从信息不完全到信息完全，从一个小方面逐渐演化至全局，即未来状态具有不确定性；③在洪水信息不完全的情况下所制定的方案需要可以便于在信息完全时刻下及时的调整。因此，施工度汛过程可以根据当前状态和逐步完善的信息来分析度汛过程趋势并对后续过程进行预测。换言之，在施工度汛过程中，当前状态对后续过程存在一定影响，而前期过程只能通过当前的状态去影响后续过程，即施工度汛具有无后效性。

1.2 马尔科夫链

马尔科夫链是一种描述复杂系统状态转移的数学模型，利用该模型求解多阶段决策过程问题[13]，过程的状态必须具备无后效性，即当前系统状态只与前一个系统状态和行动有关，更早之前的状态和行动对当前状态无直接影响。而水利水电施工度汛过程是动态变化且无后效性的，符合马尔科夫链应用的基本条件。并且，汛期来临前需要作出临时的资源调度决策，决策者就目前的洪水信息以及现阶段施工进度情况确定下一阶段的度汛方案，并在这个过程中，根据信息的不断完善，来及时调整所采取的应急方案，降低风险。因此，施工度汛风险具有马尔科夫特征，可以应用马尔科夫链理论来解决水利水电工程施工度汛应急资源调度问题[14]。

2 基于马尔科夫链的施工度汛应急资源动态调度规划模型与算法

2.1 原则设定

本文将在危机状态下，若不采取相应措施就会造成影响范围扩大，甚至在更大范围内产生严重后果的地点称为危机处理点。在施工过程中遭遇度汛风险，存在n种可能发生的危机状态S1，S2，…，Sn，记危机状态之间的转移概率为Pij(i,j=1，2，…，n)。

假定1：在遭遇大洪水风险下，道路运输能力满足应急资源的运输强度。

假定2：当施工度汛过程中遭遇洪水时，只需将足够数量的应急资源及时运抵危机处理点便可保证安全度汛；倘若调运的应急资源数量不足，则只能避免超标洪水所造成的部分损失，保障率b取值范围为0%～100%。

2.2 模型构建

马尔科夫链理论分析方法在施工度汛应急资源优化调度过程中的应用如图1所示。

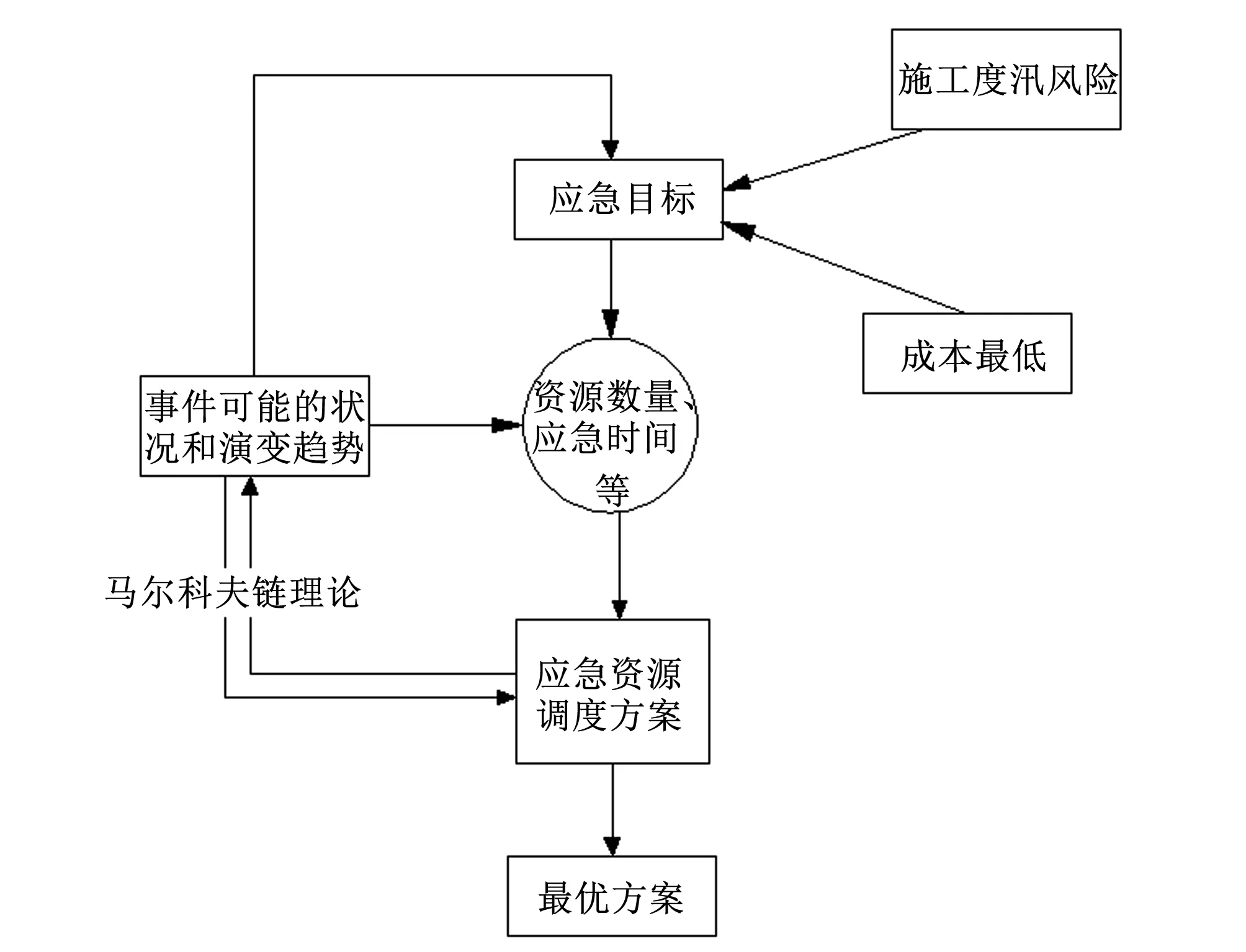
图1 马尔科夫链理论解决施工度汛应急资源调度问题的逻辑关系

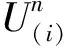
(1)

这就是马尔科夫链理论解决动态调度规划问题的基本方程。

采用z变换分析方法得到马尔科夫链理论解决施工度汛应急资源调度问题的基本方程组：

(2)

2.3 算法实现

具体算法如下。

步骤1：确定施工度汛不同危急状态为S1，S2，…，Sn。

步骤2：根据各危急状态下所需应急资源量和资源存放点位置，确定出若干种资源调度方案。

步骤3：确定各危急状态下转移概率和概率成本，计算期望成本。

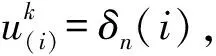
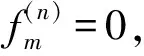
步骤7：若所得方案χn+1与前次迭代所得的方案χn完全一致，则停止迭代，从而得到资源调度的最优方案，否则返回到步骤5，令n=n+1。

3 案例分析

为了验证模型对施工度汛应急资源调度动态优化的有效性，此处利用案例来加以分析说明。

ZT水电站一级水电站施工采用明渠分期导流。:一期由主河床过流，二期由导流明渠导流，三期由已建成的1号、2号泄洪闸导流。施工导流二期围堰布置如图2所示。汛期施工为11月至次年3月，其天然来水流量如表1所示。

为了验证本模型有效性，将施工度汛期间遭遇洪水的可能性分为小洪水和特大洪水2个极端危急状态，2种危急状态之间可相互随机转换。《水文情报预报规范》中划分洪水量级的标准为[15]：水文要素重现期小于20%为小洪水，大于2%为特大洪水。记ZT水电站遭遇小洪水为危急状态S1，遭遇特大洪水为危急状态S2，调运的应急资源量与保障率b之间的关系如表2所示。

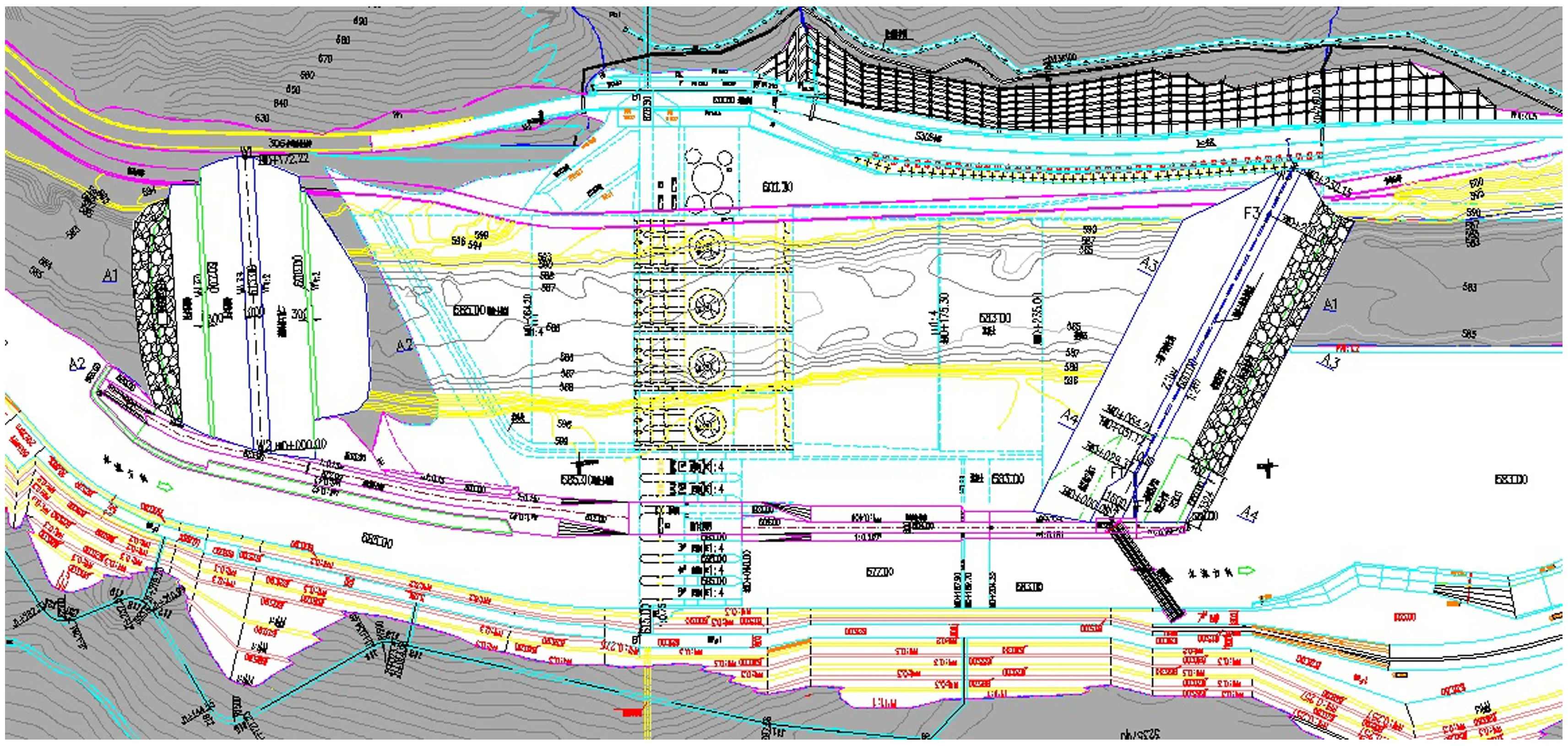
图2 ZT水电站施工导流二期围堰平面布置

频率 P/%2 5 1020洪峰流量/(m3·s-1)1 6801 5501 4501 340

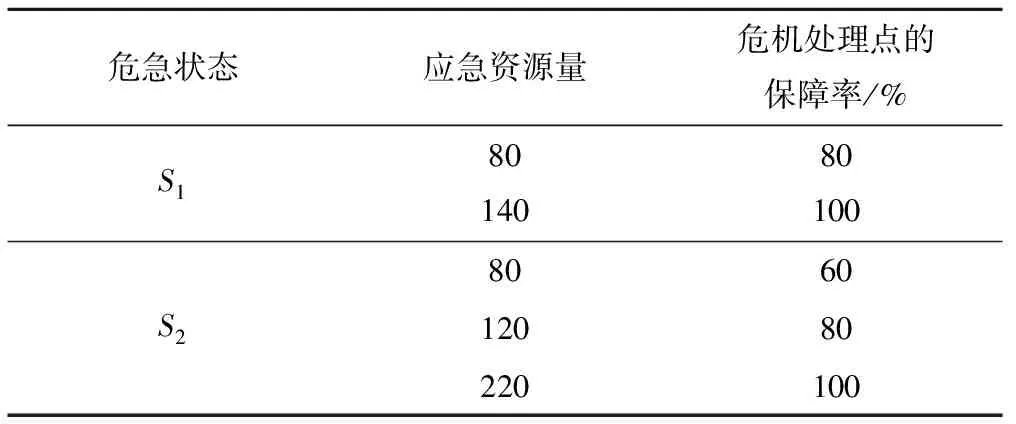
表2 资源量与保障率之间的关系

现有4个资源存放点，存放点A与危机点X距离为1个时间单位，存放点B与危机点X距离为1.5个时间单位，C、D存放点与危机X点距离为2个时间单位，各资源存放点与危机处理点X的位置关系及各资源存放点储存资源量如图3所示(考虑地形因素，资源存放点与危机处理点距离已包括水平距离和垂直距离)。

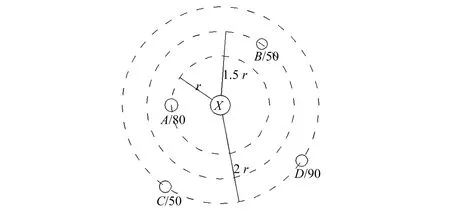
图3 资源存放点示意

现规定危机处理点的保障率为100%时为安全度汛，在此条件下，资源存放点A距危机点最近，为满足应急时间最短，尽可能多地选用存放点A所储资源。当度汛危机状态为S1时，资源存放点A储存的资源全部运送至危机点，此时危机点保障率为80%，无法满足安全度汛的需要，故需从存放点B、C、D调运60单位的应急资源至危机处理点方可满足安全度汛。当度汛危急状态为S2时，资源存放点A储存的资源全部运送至危机点，此时危机点保障率为60%，无法满足安全度汛的需要，故需从存放点B、C、D调运140单位的应急资源至危机处理点方可满足安全度汛。

因此，本案例的状态空间为S={S1,S2}，策略空间用调度方案表示，调运量与运输成本如表3所示，各方案转移概率如表4所示。

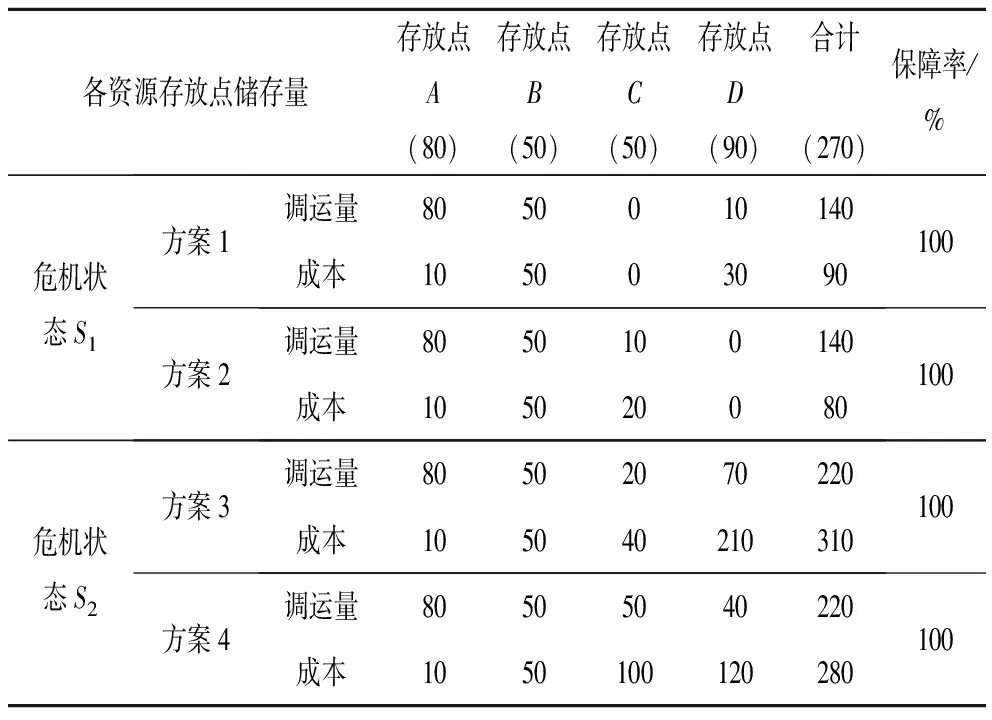
表3 各资源存放点调运量与运输成本

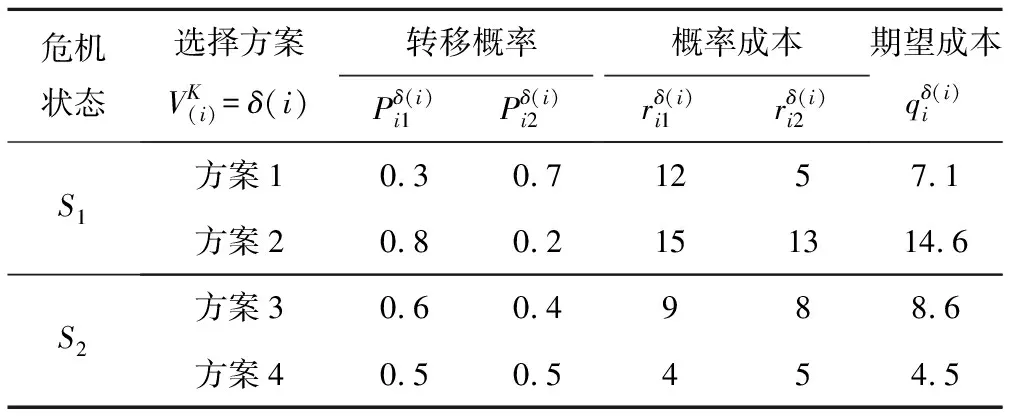
表4 危急状态转移概率和期望成本

马尔科夫决策求解过程如下：

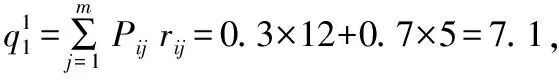
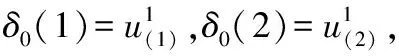
第2步，开始定值计算，并估计初始策略：

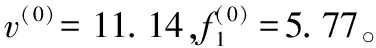
第3步，策略改进阶段，求解改进策略χ1。

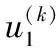
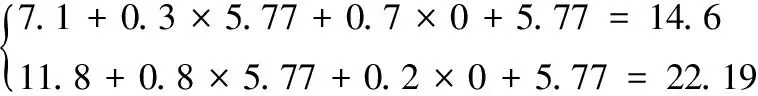
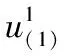
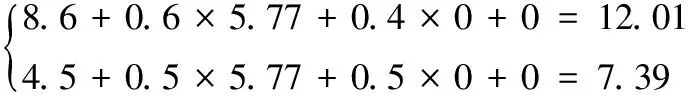
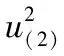
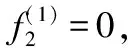
第5步，寻求改进策略χ2。

对状态S1有：

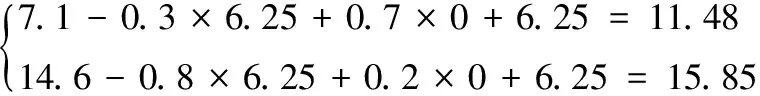
对危机状态S2有：

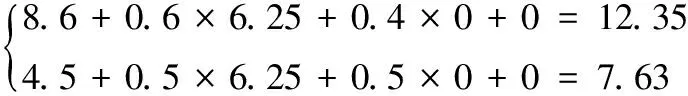
在二期明渠导流的汛期施工过程中偶遇小洪水，围堰出现纵向裂缝，需要调运应急资源，以控制围堰险情。项目负责人选择调度方案1，从相应的资源存放点调运资源，及时控制住围堰裂缝发展并修补围堰，保证了度汛安全。

4 结 论

本文为保证在有限资源下水利工程施工安全度汛，根据施工度汛特点建立了基于马尔科夫链的施工度汛应急资源的动态调度模型，可得到以下结论。

(1)诸多文献证明洪水的成因、时间分布、空间分布以及洪水波运动等都非常复杂。而目前技术手段对洪水只能进行水文预报，无法准确预测出洪水的演变过程。在此条件下，施工度汛应急资源的调度问题便成为保证汛期安全施工的重要环节。当出现施工度汛风险时，决策者需要根据现有施工度汛风险资料作出应急资源调度决策，将应急资源及时运送至危机处理点，以保证安全度汛。

(2)施工度汛过程具有动态性、无后效性、随机性等特点，符合利用动态规划方法求解多阶段决策过程 问题的基本设定。基于马尔科夫动态决策理论，建立施工度汛应急资源调度模型，在施工度汛应急资源有限的约束条件下，考虑施工度汛的动态变化特征，计算在遭遇小洪水和特大洪水2种危急状态下各自的期望成本，平衡安全度汛与度汛成本最低，在已有方案中选择出最优调度方案，从而保证安全度汛。

(3)施工度汛应急资源调度不仅要保证安全度汛，还要尽量降低应急成本。理论上，施工度汛应急资源调度方案有无数种，但本文模型实在有限的调度方案中选择最优方案，具有一定局限性。