支持向量机在河套地区地下水矿化度预测中的应用

赵 令，苏 涛，周 亮，樊 宇

(安徽理工大学测绘学院，安徽 淮南 232001)

内蒙古河套灌区属于自流引黄灌区。作为其中最大的灌域，义长灌域的农业生产对该地区的农业发展和全国商品粮食供应有重要意义[1]。土壤盐渍化问题是制约该地区农业生产与发展的主要因素之一，有效地防治土壤盐渍化对灌域至关重要。而地下水矿化度的大小与土壤盐碱化程度密切相关，同时地下水矿化度也是灌域用水管理的重要依据。因此，对灌域地下水矿化度的监测与预测尤为重要，有利于对灌域进行合理的土地利用规划，促进该地区的农业发展。

支持向量机是作为数据挖掘中的一项新技术，通过建立最优分类超平面将实验样本准确地区分，即借助于最优化方法解决机器学习问题[2,3]。当前，支持向量机在地下水动态监测以及水质评价等方面已经广泛应用，且取得很多成果，如：张霞等[4]提出了基于支持向量机的陕西省洛惠渠灌区地下水动态预测方法，很好地描述地下水动态与各因子之间响应与耦合关系，通过实证分析，表明该方法在灌区地下水动态预测中切实可行；司训练等[5]提出基于支持向量机的地下水质量综合评价方法简便易行、准确度高，具有很强的实用性；付俊娥等[6]建立了基于支持向量机的西北干旱地区地下水位遥感监测模型，模型拟合结果与实际相符，可以为西北干旱区水循环研究和流域水资源管理提供技术手段。

本文在前人研究基础上，尝试以内蒙古河套地区义长灌域作为实验区，利用灌域1990-2009年的蒸发量、引水量、地下水埋深以及矿化度等数据，建立基于支持向量机的灌域年均地下水矿化度预测模型，并与多元回归预测模型和BP神经网络预测模型进行精度对比分析，探讨支持向量机方法在研究灌域年均地下水矿化度预测中的可行性，以期为改善灌域土壤次生盐渍化现象、实现农业可持续发展提供新方法。

1 研究区概况与数据采集

1.1 研究区概况

义长灌域位于内蒙古河套灌域东北部，地理位置约为107°37′19″～108°51′04″E、40°45′57″～41°17′58″N，东西长约106 km，南北宽约48 km。灌域灌溉面积186 420 hm2，占总土地面积的55.6%。灌域整体地势平坦，西南较高东北较低，坡度从1/10 000变化到1/5 000。灌域为温带大陆性气候，年平均气温为6.1 ℃，多年平均降水量约为172 mm，且降雨集中在夏季；蒸发量在2 117 mm左右，降水少，蒸发量大，气候干燥。灌域是典型的引黄河水自流灌域，灌溉方式多以漫灌为主，但由于降雨极少、蒸发旺盛，灌域内河沟多为短小山洪沟，多年平均年径流深在10 mm左右。灌域境内地下水位较高，地下水埋深一般不超过2.5 m，其中夏灌和秋浇时期地下水位最高，地下水埋深在1.25 m左右；灌域每年会经历一段时间的冻结期，此时也是地下水位低谷期，地下水埋深下降到2.5 m左右。此外，灌域境内居民用水对地下水埋深和矿化度的空间变化也有一定影响[7]。由于灌域地下水位的上升会导致土壤表层盐分含量增加，因此，该地区土壤极易出现次生盐渍化现象。

1.2 数据采集

河套灌域内布有220个观测井对灌域地下水位进行长年观测，其中义长灌域40眼为地下水质观测井，对灌域地下水质及水状况进行长期监测。本文对义长灌域内40个观测井(见图1)的长年观测数据整理分析，得到1990-2009年间地下水埋深以及矿化度等数据。由于引起灌域地下水矿化度变化的因素有很多，本文选取该地区年均地下水埋深作为灌域年均地下水矿化度的主要影响因子。同时，引入年蒸发量与引水量作为预测模型辅助参数。

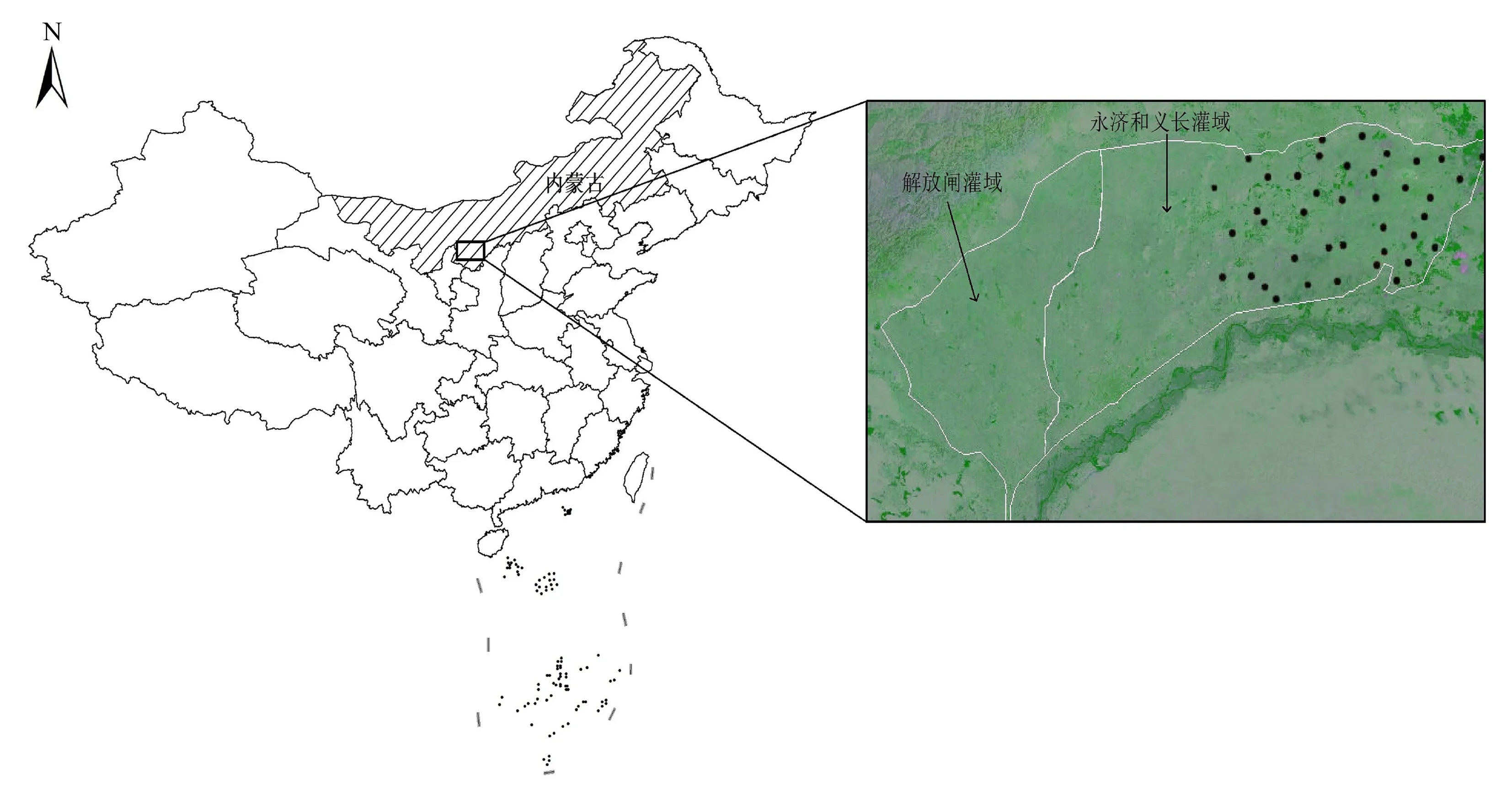
图1 研究区观测井位置

灌域农业灌溉模式直接影响着该地区地下水埋深的变化，浅层地下水矿化度也随农业灌溉灌水量的增加而增加。因此，地下水矿化度的变化在一定程度上与地下水埋深存在必然的联系。由于地下水埋深与矿化度容易受到气候、灌溉模式以及土壤类型等多种因素影响，分析短时期内地下水埋深与地下水矿化度的变化规律很难找到它们之间的联系，因此考虑以年为时间单位，对灌域20 a的年均地下水埋深与矿化度进行相关性分析。由图2可知，这期间年均地下水矿化度随着年均地下水埋深的增大而减小，其决定系数R2=0.440 7，2者具有一定的相关性。所以，选取年均地下水埋深作为预测年均地下水矿化度的主要影响因子切实可行。

图2 地下水矿化度与地下水埋深的关系

2 灌域地下水矿化度预测模型

本文样本数据来源为义长灌域1990-2009年观测数据，其中1990-2004年间的15组样本数据作为构建年均地下水矿化度预测模型的训练样本，2005-2009年间5组样本为测试模型的检验样本。由于上述影响因子量纲不同，故将各影响因子数据进行归一化处理到[0,1〗之间[8]。

2.1 多元回归预测模型的建立

含有n个自变量和单个因变量的多元回归模型一般形式为：

y=b0+b1x1+b2x2+…+bnxn

式中：xn为自变量；y为因变量；bn为参数。

本文建立的多元回归预测模型有3个自变量，x1、x2、x3分别对应蒸发量、引水量以及年均地下水埋深，因变量y对应年均地下水矿化度。借助Spss软件对1990-2004年间的15组训练样本数据进行多元回归分析，得到灌域年均地下水矿化度多元回归模型：

y=5.366-1.228x1+1.112x2-1.368x3

2.2 BP神经网络预测模型的建立

(1)模型原理。BP神经网络是当前应用最为广泛的神经网络之一，具有良好的非线性映射及自学习能力，相比于其他传统模型，BP神经网络模型的持久性和预测性更为出色[9-11]。BP神经网络模型建模方法就是在确定各层节点数的基础上通过不断地调整权重系数使总误差达到最小，从而达到预期效果。

(2)模型建立。研究表明[12]，建立3层BP神经网络即可满足本文要求。本文借助Matlab 2014软件建立灌域年均地下水矿化度BP神经网络预测模型。首先，对权值和阈值初始化，给定输入x和期望输出y。文中BP神经网络模型输入节点数为3个，输入因子分别为蒸发量x1、引水量x2、年均地下水埋深x3。输出节点数为1个，输出因子为年均地下水矿化度y。然后，信息从输入层传入，经过隐含层处理，正向计算输出y。如果实际输出与期望值不符，即期望误差较大不满足计算要求，则输出将按原路径反向传播，不断修正各层连接权值ω，达到期望误差最小。一般来讲，隐含层节点数的选择无法确定，通常根据经验公式所得，本文求得隐含层神经元个数3～12。模型训练函数为Trainlm，最大迭代次数为50 000，训练目标最小误差为 0.001，输出层选择的函数为Purelin，学习效率0.05。同时，选取均方根误差为该模型精度主要评价指标。通过调整隐含层节点数，确定本研究网络拓扑结构为3∶6∶1(见图3)时，网络表现出较好的误差收敛性，且泛化能力强、误差最小，此时模型训练最优(RMSE= 0.06)。 值得注意，网络在每一次训练结束可以收敛到最小值，但不能保证在每一次训练后收敛到全局最小。因此，在具体实践中要根据实际情况选择最优模型。

图3 BP神经网络原理示意

2.3 支持向量机预测模型的建立

2.3.1 支持向量机基本理论

支持向量机是基于统计学习理论发展起来的，根据结构化风险最小原则提高学习机推广能力[13,14]。其基本原理是通过实现经验风险和置信范围的最小化，进而获得良好的统计规律[15,16]。因此，支持向量机能够很好地处理许多小样本问题。

支持向量机是用线性回归函数f(x)=ωx+b拟合数据{xi，yi}，i=1，2，…，n，xi∈Rn，yi∈R，假设训练数据在 精度下无误差，用线性函数拟合样本数据可解如下优化问题，即：

(1)

约束条件：

(2)

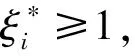
(3)

约束条件：

(4)

对于待分析样本集{xi，yi}，i=1，2，…，n，xi∈Rn为输入，yi∈Ri为输出，则支持向量机对偶形式为：

(5)

(6)

(7)

常用核函数有以下几类：

(1) 多项式核函数：K(x,y)=(xy+1)d，d=(1,2,…,n)。

(2) 径向基函数核函数：K(x,y)=exp(-γ‖x-y‖2)。

(3) Sigmoid核函数：K(x,y)=tanh[φ(xy)+θ]。

2.3.2 支持向量机预测模型的建立

支持向量机预测模型的建立同样借助Matlab 2014编写相应程序。灌域年均地下水矿化度支持向量机预测模型的建立就是寻找灌域年均地下水矿化度与其影响因子(蒸发量、引水量、年均地下水埋深)之间的关系，即寻求公式(7)的成立，x为地下水矿化度的影响因子，xi为k个样本中的第i个样本，K(x,xi)为核函数。在建立SVM回归模型过程中，模型精度的高低取决于模型参数的选择，其中主要影响模型精度的参数为惩罚因子参数C和核函数参数g。本文输入向量分别为蒸发量、引水量、年均地下水埋深，输出为灌域年均地下水矿化度。再确定学习样本后，此模型的建立主要是选择相应的核函数和惩罚因子参数C。通过对上述3类核函数的测试，本研究的支持向量机预测模型的核函数为径向基函数。利用网格搜索法求得模型的最优惩罚因子参数C和核函数参数g，确定最优参数C=2，g=0.35。最后，根据式(5)、式(6)得到灌域年均地下水矿化度支持向量机预测模型。

3 结果与分析

3.1 模型预测精度对比分析

分别用以上3种模型对2005-2009年间的灌域年均地下水矿化度进行预测，表1为通过3种模型得到的年均地下水矿化度预测值与实测值的比较，其中包括3种相对误差和绝对误差的比较。可以看出，多元回归模型的平均误差为0.47 g/L，最大误差为1.15 g/L；BP神经网络预测模型平均误差为0.20 g/L，最大误差为0.38 g/L；支持向量机预测模型平均误差为0.15 g/L，最大误差为-0.21 g/L。BP神经网络预测模型与多元回归预测模型相比，其平均误差和最大误差分别降低了57%和67%；支持向量机预测模型与多元回归预测模型相比，平均误差和最大误差分别降低68%和82%；支持向量机预测模型与BP神经网络预测模型相比，平均误差和最大误差降低了25%和45%。由此可见，BP神经网络预测模型与支持向量机预测模型都取得了相对较好的预测结果，但支持向量机预测模型预测效果最佳，明显优于多元回归预测模型与BP神经网络预测模型，其预测精度最高。

表13种模型预测值与实测值比较g/L

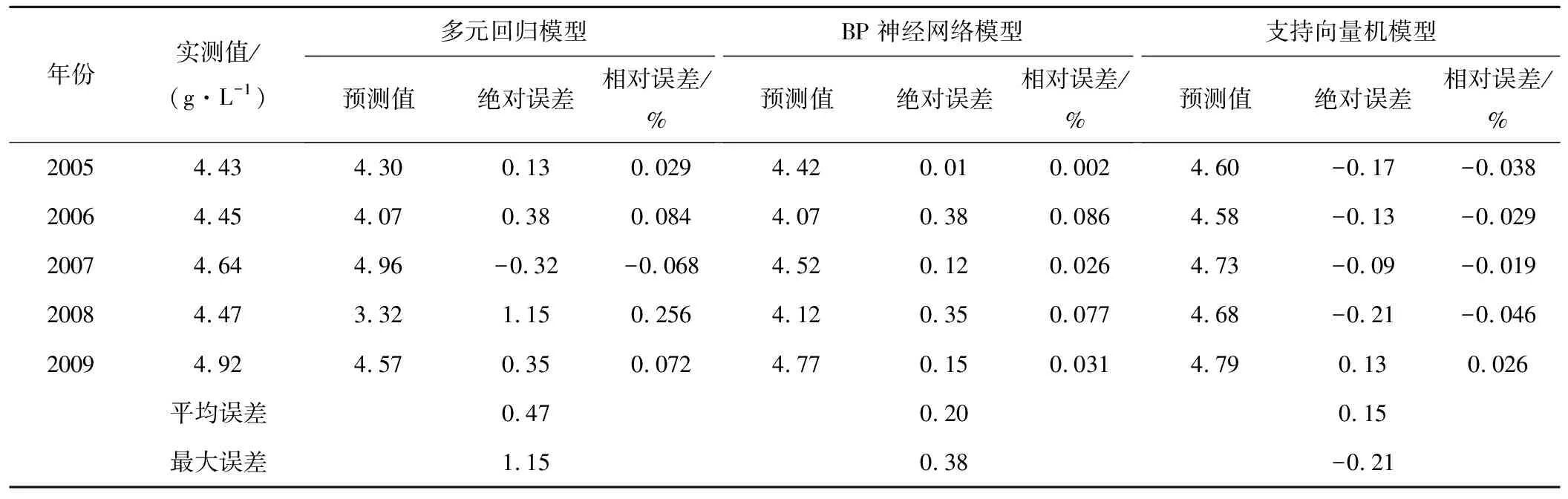
年份实测值/(g·L-1)多元回归模型预测值绝对误差相对误差/%BP神经网络模型预测值绝对误差相对误差/%支持向量机模型预测值绝对误差相对误差/%20054.434.300.130.0294.420.010.0024.60-0.17-0.03820064.454.070.380.0844.070.380.0864.58-0.13-0.02920074.644.96-0.32-0.0684.520.120.0264.73-0.09-0.01920084.473.321.150.2564.120.350.0774.68-0.21-0.04620094.924.570.350.0724.770.150.0314.790.130.026平均误差0.470.200.15最大误差1.150.38-0.21

3.2 预测结果相关性分析

由表2和图2看出，多元回归预测模型的预测值与实测值相差较大，其变化曲线变化幅度明显，尤其是在2008年绝对误差达到1.15 g/L，说明在检验样本较少的情况下，多元回归预测模型对灌域年均地下水矿化的预测具有不稳定性，预测值与实测值相关性R2=0.28，预测效果不是很理想。BP神经网络预测模型预测值与实测值逐年变化趋势大体相同，但在2006年和2008年得到的预测值偏离实测值较多，分别达到0.38和0.35 g/L，预测值与实测值相关性R2=0.72，预测精度明显提高。对比以上2种预测模型，支持向量机预测模型所得到的预测值变化曲线与实际变化曲线最为接近，且变化趋势一致，平均误差最小，仅为0.15 g/L，预测值与实测值相关性R2=0.81，预测效果最为理想，能够很好地反应研究区年均地下水矿化度在2005-2009年的实际变化情况。

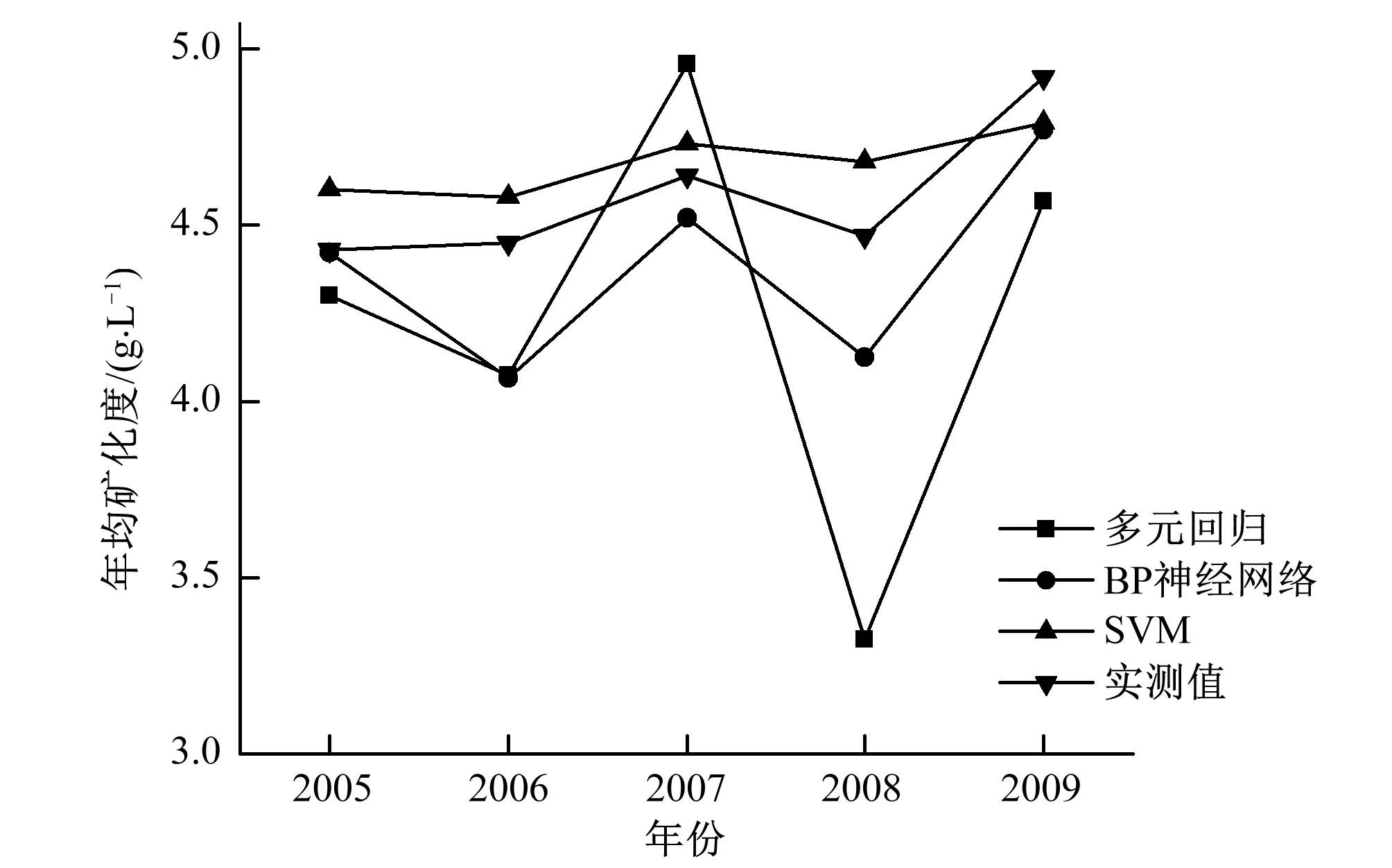
图4 3种模型预测值与实测值对比

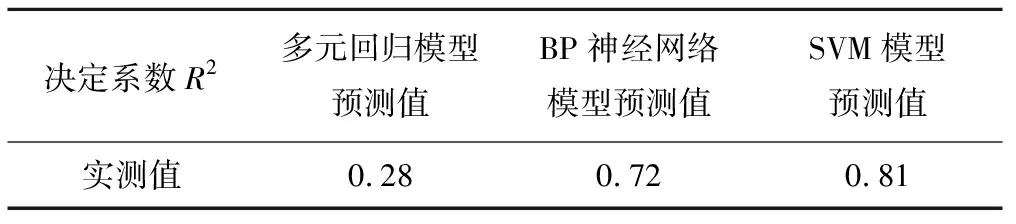
决定系数R2多元回归模型预测值BP神经网络模型预测值SVM模型预测值实测值0.280.720.81

4 结 论

本文为探究义长灌区地下水矿化度长年变化规律，建立了基于支持向量机的内蒙古义长灌域年均地下水矿化度预测模型，并与多元回归预测模型和BP神经网络预测模型进行对比，得出以下结论。

(1)本文建立的3种预测模型(多元回归模型、BP神经网络模型、支持向量机模型)最大误差分别为1.15、0.38、-0.21 g/L，平均误差分别为0.47、0.20、0.15 g/L。可见，3种模型中支持向量机预测模型预测效果优于BP神经网络预测模型，而BP神经网络预测模型预测效果优于多线回归预测模型。

(2)通过实测数据对3种模型进行验证，多元回归预测模型预测值与实测值相关性较低，R2仅有0.28，预测效果不佳。BP神经网络预测模型、支持向量机预测模型预测值与实测值相关性分别是R2=0.72和R2=0.81。可见，BP神经网络预测模型和支持向量机预测模型都能够较大地提高了灌区年均地下水矿化度的预测精度，其中支持向量机预测模型预测效果最好。

(3)灌域地下水矿化度受很多因素影响，通过利用支持向量机的方法，能够以较少因子对灌域多年平均地下水矿化度进行预测而取得良好的效果，说明支持向量机模 型在长年地下水矿化度监测方面有很好的适用性，为灌域地下水研究和生态环境改善提供新思路。