例谈全国卷Ⅰ（理科）中的数列问题

☉湖北省荆门市第一中学 王韵萱

全国卷Ⅰ历年的高考试题中数列题目出现的情况一般有两种：一是选择题和填空题各一道，分值10分；二是只有一道解答题，分值12分.从题目难度上来看，数列解答题一般难度都不是太大，即便是选择题和填空题也一般为中档题，当然有时数列题目偶尔也会出现在选择题或者填空题的最后一题，题目较难.接下来笔者就以新课标全国卷Ⅰ历年的高考试题为例来分析一下这些题目的解决方法.

一般我们将数列问题分为两大类：有通项式类和无通项式类.

一、无通项式类

无通项式类问题中的通项公式一般难以求出或根本不能求出，这时候就需要我们对题干中的已知条件进行一些适当的转换进而来得到问题的答案，这类问题一般出现的概率比较小.而此类问题解题的关键在于怎样将题干中的已知条件通过适当的转换一步步化为我们所求的目标，下面通过几个例题来说明.

例1（2009年新课标理科卷Ⅰ，第14题）设等差数列{an}的前n项和为sn，若s9=72，则a2+a4+a9=______.

解析：这道题目仅知道数列的前9项和，也就是说只知道a5=8，通过观察所求式子，不难发现a2+a4+a9=3a5，即所求答案为24.

例2（2012年新课标理科卷Ⅰ，第16题）数列{an}满足an+1+（-1）nan=2n-1，则{an}的前60项和为______.

解析：看到（-1）n这一项，根据经验可以想到将n分奇偶来求解.

可得出奇数项和为15×2=30，偶数项和为8（1+3+5+…+29）=1800，即前60项和为1830.

二、有通项式类

有通项式类的数列题目比较多，一般来说难度与跨度都比较大，通常在解答题中为中档题，选择题和填空题有个别难题.通过以下几个例题来说明这一类题目的解题方法和解题思路.

例3（2012年新课标理科卷Ⅰ，第5题）已知{an}为等比数列，a4+a7=2，a5a6=-8，则a1+a10=（ ）.

解析：等比数列已知两个条件，则一般通过这两个条件可求出通项.通过观察a5a6=-8可化作a4a7=-8，又a4+a7=2，则可以解出a1+a10=a4q-3+a7q3=-7.故选D.

例4（2016年理科卷Ⅰ，第3题）已知等差数列{an}的前9项和为27，a10=8，则a100=（ ）.

解析：这道题目属于比较容易的数列题，由题明显可以得到a5=3，由a10=8可以得到通项an=n-2，则a100=98.故选C.

例5（2017年理科卷Ⅰ，第12题）已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，在接下来三项是20，21，22，以此类推.求满足如下条件的最小整数N：N＞100且该数列的前N项和为2的整数幂，那么N为（ ）.

解析：通过题目可以找到规律.第m组有m项，分别为20，21，22，…，2m-1.

第m组的和为2m-1，前m组的和为2m+1-m-2，

由于N＞100，则，则m≥14，

若要使前N项和为2的整数幂，设，则项的和2k-1应与-2-m互为相反数，即2k-m-3=0，由m≥14，则k≥5.k=5时，m=29，此时

故选A.

例6（2018年理科卷Ⅰ，第14题）记Sn为数列{an}的前n项和，若Sn=2an+1，则S6=______.

解析：这道题很明显可以求出通项，

再将n=1代入原式可得a1=-1，

接下来我们来说一说有关数列题目的解答题，如果高考中数列题目出现在解答题上，就一定出现在第17题的位置上.第17题作为解答题的第一道题目，一般不会太难，而且通常会有两问，第一问根据已知条件求数列的通项公式，第二问根据已知条件求数列的前n项和，解题方法一般也很固定，只要按照正常的解题步骤一步步规范解答就没有任何问题.

例7（2015年理科卷Ⅰ，第17题）Sn为数列{an}的前n项和，已知an＞0，an2+2an=4Sn+3.

（1）求{an}的通项公式.

解析：（1）当Sn和an同时出现在一个等式中时，一般利用an=Sn-Sn-1（n≥2）来进行求解.

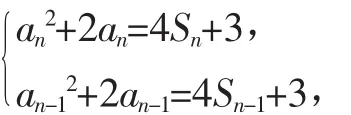
两式相减整理可得（an+an-1）（an-an-1-2）=0.

由于an＞0可得（an-an-1-2）=0，即an-an-1=2.

令题目中等式的n=1，可得a1=3.

所以{an}是首项为3，公差为2的等差数列，通项公式为an=2n+1.

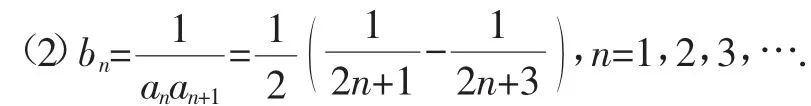
设数列{bn}的前n项和为Tn，则数列{bn}的前n项和

例8（2014年理科卷Ⅰ，第17题）已知数列{an}的前

n项和为Sn，a1=1，an≠0，anan+1=λSn-1，其中λ为常数，

（1）证明：an+2-an=λ.

（2）是否存在λ，使得{an}为等差数列？并说明理由.

解析：（1）与上题一样有Sn和an同时出现在一个等式中，利用an=Sn-Sn-1来进行求解.

由an≠0可得，an+2-an=λ.

（2）假设存在λ，使得{an}为等差数列，则将n=2代入题目中等式可得a2=λ-1，a3=λ+1，a3-a2=2，要使{an}为等差数列，则a2-a1=λ-2=2，即λ=4，此时an=2n-1为等差数列.

历年来的理科卷Ⅰ中数列题目必定会出现，出现的方式可能是一道选择题外加一道填空题，也可能是第17题.这些题目的难度一般不是很大.在历年的理科卷Ⅰ中，只有2012年和2017年这两年的高考题的数列题目分别出现在第16题和第12题的位置上，难度较大.做数列题目的关键在于如何根据题干中的已知条件厘清思路，明确这道题是否需要求出其通项公式及前n项和，如果需要求出其通项公式，就需要观察题干中给出的已知条件，思考要用什么方法求其通项公式及前n项和.如果不需要求出其通项公式及前n项和，就需要思考其转化的方式，必要时可使用公式进行一些适当的变形.

总之，高考中的数列题目一般难度不会太大，解题方法和思路一般也不会超出我们所学的常用的几种基本方法，其关键之处在于规范细致.做题时一定要看清题干中给出的已知条件和所要解决的问题，认真审题，细心解题，规范答题，相信在以后的高考中遇到数列题目我们都能迎刃而解.