核心素养巧引领，逻辑推理妙应用——例谈实际应用问题中的逻辑推理

☉浙江省丽水中学 周杰华

逻辑推理作为高中数学的六大核心素养中的主要内容之一，备受各方关注，是数学学科教学与学习过程中必备的一项技能，逻辑推理是从一些理论事实、命题等角度出发，依据题目中已知的规则来推出其他相关命题或结论的基本素养．逻辑推理根据推理的方式可分为归纳或类比（从特殊到一般的推理）与演绎（从一般到特殊的推理）．下面对近几年高考中比较常见的以实际生活为背景的逻辑推理问题加以剖析．

一、信息推理

例1A，B，C，D四位同学一起去向英语老师询问英语竞赛的成绩情况．英语老师说：“你们四人的竞赛成绩中有2位优秀，2位良好，我现在给A看B，C的成绩，给B看C的成绩，给D看A的成绩．”看后A对大伙说：“我还是不知道我的成绩．”根据以上相关信息，则（ ）.

A．B可以知道四人的成绩

B．D可以知道四人的成绩

C．B，D可以知道对方的成绩

D．B，D可以知道自己的成绩

分析：依据题目中的已知条件，抓住题设的关键可得到：A看了B、C的成绩后而不知道自己的成绩，由此可以推断：B，C（或A，D）的成绩均是1位优秀、1位良好，从而再结合其他相关信息：B看了C的成绩，D看了A的成绩，进而加以逻辑推理，得以确定判断．

解析：抓住关键信息可知：A看了B、C的成绩后而不知道自己的成绩，由此可以推理：B，C（或A，D）的成绩为1位优秀、1位良好；又根据条件中B看了C的成绩，进而推理可得：B可以知道自己的成绩.

同理，D看了A的成绩，从而可以推理：D可以知道自己的成绩.

故选D．

点评：本题通过对实际问题中的信息处理，结合情景推理来解决实际应用中的逻辑推理问题，主要考查逻辑推理的数学核心素养．特别地，在结合实际应用中的相关信息推理问题时，关键是要抓住问题中的相关信息要点，加以合理转化，形成相应的数学语言、数学模型等，进而利用相关的数学知识来分析、处理、判断，并加以正确的逻辑推理，使得实际应用问题得到巧妙解答．

二、图表推理

例2（2016·北京文·14）某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品共有3种，后两天都售出的商品共有4种.则该网店

①第一天售出但第二天未售出的商品共有______种；

②这三天售出的商品最少有______种.

分析：借助集合中的图表信息，并利用题目中相关的实际生活问题的数据信息，转化为求集合中的元素个数的问题，借助集合的运算与关系，以及实际情况来进行推理与分析，达到逻辑推理与应用的目的．

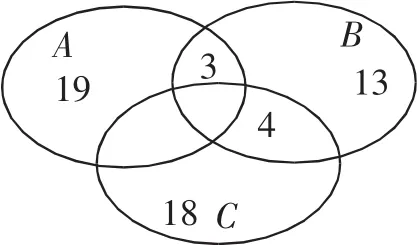
解析：通过作图分析，如图所示，A，B，C分别表示第一天，第二天，第三天售出的商品种数所构成的集合.

（1）由于前两天都售出的商品共有3种，那么第一天售出但第二天未售出的商品共有19-3=16种.

（2）要使得这三天售出的商品最少，应该使这三天都售出的商品尽可能地多，结合条件可知有3种（由于A与B的公共部分为3，B与C的公共部分为4，只能取3）；同时，第一天与第三天都售出的商品尽可能的多，结合条件可知可以为17种（C中与B没有公共的部分有18-4=14，A中与B没有公共的部分有19-3=16，则取14，同时加上这三天都售出的商品3件，共有14+3=17），这样这三天都售出的商品最少，最少为19+（13-3）=29种.

故填答案：①16；②29．

点评：在实际生活中应用逻辑推理时，经常借助集合的Venn图、数轴以及统计的图表、树状图、表格等相应的图表直观信息来转化，把题目中的实际生活问题借助数学模型进行直观转化与处理，结合实际情况加以合理分析，再通过反馈来解决实际应用问题．

三、数字推理

例3三张不透明的卡片上分别写有数字1和2，1和3，2和3．A，B，C三人分别从中取出一张卡片，A看了B的卡片后说到：“我与B的卡片上相同的数字不是2.”B看了C的卡片后说到：“我与C的卡片上相同的数字不是1.”C说到：“我的卡片上的数字之和不是5.”由此可以判断A的卡片上的数字是______．

分析：从C说的内容入手来分析C的卡片上的数字的可能性，结合B说的内容即可判定B的卡片上的数字，再结合A说的内容即可准确推理与分析出A的卡片上的数字．

解析：根据题目中C说的“我的卡片上的数字之和不是5”可知，C的卡片上的数字不是写有2和3，那么C的卡片上数字可能是：1和2，1和3.

由B说的“我与C的卡片上相同的数字不是1”可知，B的卡片上的数字是2和3.

再由A说的“我与B的卡片上相同的数字不是2”可知，A的卡片上的数字是1和3.

故填答案：1和3．

点评：通过对题目中的数字的推理，结合数字之间的关联来解决实际生活中的应用问题，往往是数学中逻辑推理最常见的类型之一，通过数字之间的联系、运算等加以巧妙地设置问题，利用数学知识的推理、运算、分析来化归与转化，进而达到用正确地逻辑推理来解决实际问题的目的．

四、综合推理

例4某无人机兴趣小组由若干名教师和学生组成，根据该兴趣小组中的人员分析可知：

（ⅰ）女学生的人数少于男学生的人数；

（ⅱ）教师的人数少于女学生的人数；

（ⅲ）教师的人数的两倍多于男学生的人数．

①若教师的人数为4，那么女学生的人数的最大值是______．

②该学习兴趣小组人数的最小值是______．

分析：先设出相应的男学生人数为x，女学生人数为y，教师人数为z，结合题中的已知条件建立不等式以及相关参数的取值范围，结合z=4，利用自然数的性质来确定女学生人数的最大值；结合题目条件得到2z-z≥3，并结合条件确定z的最小值，再利用自然数的性质与不等式的关系来确定此时x，y的值，进而确定该小组人数的最小值．

解析：设男学生人数为x，女学生人数为y，教师人数为z.

根据题目中的三个已知条件可得：2z＞x＞y＞z，且x，y，z∈N*.

（1）由于z=4，则有8＞x＞y＞4，要使得女学生人数最大，即y取得最大值，只能是x=7，y=6，此时ymax=6；

（2）由于2z＞x＞y＞z，且x，y，z∈N*，那么必有2z-z≥3，解得z≥3，要使得该小组人数最小，则z取最小值zmin=3，此时有6＞x＞y＞3，可得x=5，y=4，此时x+y+z=5+4+3=12.

因此该兴趣小组人数的最小值为12人.

故填：①6；②12．

点评：通过实际生活问题的相关信息建立相应的数学模型，结合题目信息与数学知识之间的联系加以逻辑推理，可以转化为相应的函数关系式、不等式（组）、方程以及其他相关的数学问题，再利用对应的数学模型来解决，同时要注意到数学知识与实际生活问题之间的关联与差异．总之，在综合推理过程中，要注意综合信息、数字、模型等诸多条件的限制，通过综合与处理，进而达到合理应用逻辑推理来正确解题的目的．

其实，逻辑推理作为一种重要的数学核心素养，是学生在实际的数学学习过程中形成的一种重要的思维方式和推理方法，并能有效地用来解决数学的相关问题，特别在解决高考数学题时，逻辑推理起着越来越重要的作用，在选择题、填空题中往往发挥着奇特功效，可以大大提高解题速度，综合提升数学解题能力．逻辑推理在我们的终生学习中更具有特殊的功能，其贵在提出和论证相关的数学命题，在掌握逻辑推理的基本形式的基础上，理解事物之间的关联，掌握知识结构，同时形成重论据、有条理、合乎逻辑的思维品质和理性精神，增强交流能力．H