基于“解决问题”的微专题复习案例设计与思考——以“导数在三次函数中的应用”为例

☉江苏省清浦中学 吴洪生

近期，本人受淮安市教研室的委托，为本市特级教师工作室的老师上了一节“基于解决问题的微专题复习”展示课，现将上课前后的心路历程呈现出来.本课立足于一道考题，从母题出发，建构三次函数的图像特征，对一些零散的知识进行串联，运用变式巧妙挖掘，既能探究解决问题的通性通法，又能依据问题的特点寻求简化解法，教会学生如何思考，培养和提高学生“解决问题”的能力.

一、案例设计

导数及其应用在江苏高考中地位突出，常考常新.三次函数更是高考的高频考点，在全国各地的模考与高考中争奇斗艳，特别是三次项的系数含参的三次函数问题更成为各地竞相展演的重点，真可谓“你方唱罢我登场”.

1.课前热身（课前10分钟）

（1）（教材改编）函数f（x）=x3-3x-1的单调减区间为______.

（2）（2016苏州模拟）已知f（x）=x3+3ax2+bx+a2在x=-1时有极值0，则a-b=______.

（3）函数f（x）=x3-ax-1在（-2，+∞）上既有极大值又有极小值，则a的取值范围为______.

（4）（2016扬州模拟）函数f（x）=x3-3x+a有三个零点，则a的取值范围为______.

设计意图：教材中导数的应用主要讲两个方面，一是用导数研究函数的单调性，二是用导数研究函数的极（最）值.函数的单调性与极（最）值是研究函数的重要基础，函数其他性质的研究最终都要落实到这二者上.以上四个小题都很基础，目的是深化学生对基础知识以及重要考点的理解与掌握.

2.问题提出

母题（2008江苏高考14题改编）已知函数f（x）=ax3-3x+1，讨论f（x）的单调性.

设计意图：母题是本节课的“魂”.设计目的有五个：一是探究三次项的系数含参的函数单调性；二是借助本例题探索一般三次函数的图像特征；三是利用三次函数的图像特征深化研究有关三次函数性质的问题；四是适当降低难度，搭建台阶，为解决2008年江苏高考第14题作铺垫；五是期望以母题为出发点，进行一题多解、一题多变、一题多用的训练，使学生能够多层次、广视角、全方位地认识问题，全面深化“解决问题”的能力.

3.合作交流

师：请同学们按独立思考、小组交流、成果展示这样的流程探究母题.

生1：f′（x）=3ax2-3，由于含参，首先考虑对参数进行分类讨论.

①当a≤0时，f′（x）=3ax2-3＜0对于∀x∈R恒成立，则f（x）的单调递减区间为（-∞，+∞），无单调递增区间.

②当a＞0时，

令f′（x）=3ax2-3=0，得或

易得，f（x）的单调递增区间为和单调递减区间为

师：生1同学运用分类讨论思想给出了函数的单调区间.你能由单调区间画出该函数的示意图吗？哪位同学来展示一下？

生2：

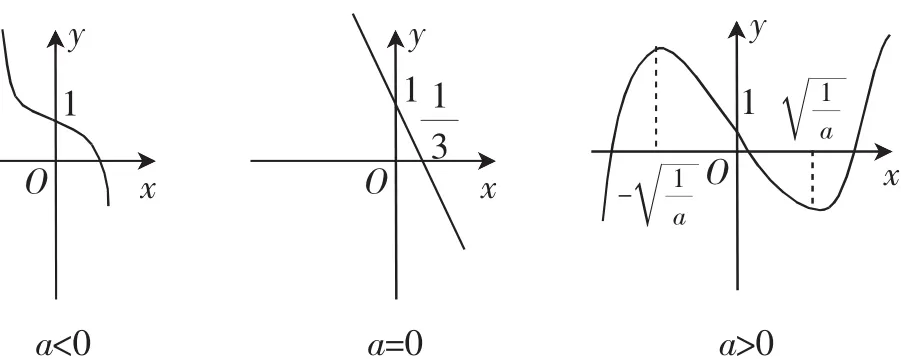
4.探究提升

师：生2同学根据函数的单调性，分三种情况画出了该函数的示意图，直观体现了函数的图像特征.如果将该三次函数一般化，同学们能参照上述的分析过程，探究一般三次函数的图像特征吗？我们约定：三次函数f（x）=ax3+bx2+cx+d（a≠0），其导函数f′（x）=3ax2+2bx+c，方程f′（x）=0的判别式Δ=4（b2-3ac）.

师生合作探究，归纳出如下结论：

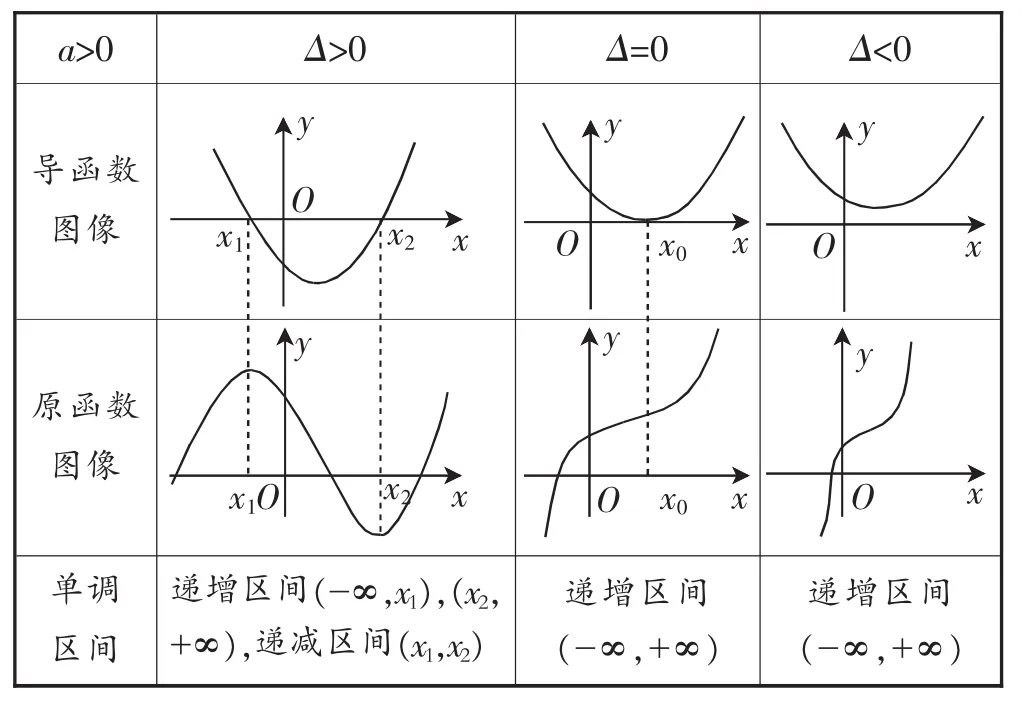
a＞0 Δ＞0 Δ=0 Δ＜0导函数图像y原图函像数xx单调 递增区间（-∞，x1），（x2， 递增区间 递增区间区间+∞），递减区间（x1，x2） （-∞，+∞） （-∞，+∞）

（a＜0时，仿上）

5.纵引横联

问题1：已知函数f（x）=ax3-3x+1在区间（-1，1）上单调递减，求实数a的取值范围.

生3：由生2所作示意图可知，（1）当a≤0时，显然符合题意；（2）当a＞0时，区间（-1，1）必为的子区间，

即0＜a≤1.

综上，a∈（-∞，1］.

生4：分两步：首先转化为恒成立问题；其次是分离参数、分类讨论.

由题可知，f′（x）=3ax2-3≤0对∀x∈（-1，1）恒成立.则

（1）当x=0时，a∈R；

（2）当x≠0时对∀x∈（-1，0）∪（0，1）恒成立，所以a≤1.

综上，a∈（-∞，1］.

设计意图：（1）引导学生感悟并理解“函数在某区间上递减（增）”即“该区间是函数单调递减（增）区间的子区间”；（2）引导学生从导函数的符号与单调性的关系出发，探究“函数在某区间上递减（增）”必有“在此区间上f′（x）≤0（f′（x）≥0）恒成立”；（3）熟练掌握用分离参数法来研究恒成立问题；（4）巩固数形结合、分类讨论、转化化归等数学思想方法的应用.

问题2：已知函数f（x）=ax3-3x+1的单调递减区间为（-1，1），求实数a的值.

生5：函数f（x）的单调递减区间就是f′（x）＜0的解集，所以

即（-1，1），

设计意图：问题2意在与问题1进行比较，让学生辨别“函数的单调递减（增）区间”与“函数在某区间上单调递减（增）”的关系.

问题3：已知函数f（x）=ax3-3x+1在区间（1，2）上不单调，求实数a的取值范围.

分析：何为“不单调”？对于连续函数（常函数除外）而言，函数在某区间内不单调，意思为函数在该区间上既有递增区间又有递减区间，可进一步理解为，函数在该区间内有极值点.因此，即

设计意图：引导学生透彻理解“函数在某区间内不单调”的含义，深化学生对函数单调性的认识.

问题4：已知函数f（x）=ax3-3x+1在区间［1，2］上存在单调增区间，求实数a的取值范围.

分析：首先，当a≤0时，f（x）在区间［1，2］单调递减，不符合题意，因此必有a＞0.

生6：由于函数f（x）在其递增区间上满足f′（x）＞0，因此函数f（x）在区间［1，2］上存在单调增区间，即f′（x）＞0在［1，2］上有解，换句话说，f′（x）＞0的解集与［1，2］有公共区间.所以，，即

设计意图：通过对关键词“存在”的理解，使学生掌握“函数在某个区间上存在单调增（减）区间”即这个区间与函数的单调递增（减）区间有公共区间.

变式1：已知函数f（x）=ax3+x2-x+c在（2，+∞）上单调递增，求a的取值范围.

变式2：已知函数f（x）=ax3+x2-x+c在（2，+∞）上存在单调递增区间，求a的取值范围.

通过对以上四个问题及两个变式的研究，指导学生对导函数、单调性、极（最）值等知识进行梳理，既理解了概念，又掌握了方法，也渗透了数学思想，学生对考点的把握达到系统化、结构化、深刻化.

6.课后思考

1.（2014辽宁高考11题）当x∈［-2，1］时，不等式ax3-x2+4x+3≥0恒成立，则a的取值范围为______.

2.（2012浙江高考17题）关于x的不等式［（a-1）x-1］（x2-ax-1）≥0对任意的x＞0恒成立，则实数a=______.

设计意图：设计思考题，意在让学生进一步感知高考试题，深化巩固用最值法和分离参数法来探究恒成立问题中的参数范围（或值），尤其是思考2在最值法、分离参数法等常规方法难以奏效的情况下，如何寻找解题突破口？可否借助三次函数的图像特征寻求解题之道？由于求的是a的值而不是取值范围，那么赋值法是否可行？这样的设计有利于提高学生分析问题、解决问题的能力，有利于培养学生的数学素养.

二、反思感悟

荷兰著名数学家弗赖登塔尔指出：反思是数学思维活动的核心和动力.从课堂实施的效果来看，本节课的教学是比较成功的，教学过程体现了教师的主导作用，突出了学生的主体地位，使学生在活跃愉快的生生合作及师生合作中完成了教学目标.课堂教学之后，笔者对本节课的教学进行了全面的回顾与小结，对此也有了更深入的思考，并发现在教学实践中存在的一些缺憾.

1.明确主题，拓展思维

本节课的课题是“导数的应用——三次函数”，主旨是“基于‘解决问题’的微专题复习”，教学过程始终围绕主题展开，精心设计问题串，为学生营造了广阔的思维空间，使学生的思维有了一定的深度和广度，较深层次地参与到教学过程之中.无论是问题的设置与环节的掌控，还是活动的展开，都循序渐进、过渡自然、水到渠成.

2.设计合理，教法恰当

本节课以高考题为载体，核心是用导数研究含参三次函数的单调性，并以此为抓手探究恒成立问题的解法，其中导数与单调性的关系在知识形成的过程中起着关键作用.笔者在教学中首先通过课前热身，帮助学生复习导数与单调性的关系，又将2008年江苏高考14题改编设计出母题，并由此展开含参三次函数单调性的探究，为最终解决该高考题搭建平台，在教学过程中对导数与单调性的关系作了细致地分析与探究，使学生可以通过对这一关系的理解，更好地把握“最值法”和“分离参数法”.

3.突出重点，深度探究

整节课在“问题”的驱动下，学生通过自主探究、合作探究等方式掌握知识、训练思维、培养能力，从而有效地突出了本节课的重点与难点.课堂上笔者设计了很多活动，从中可以看出知识是学生在自主探究中获得的，问题是学生在自我辨析中解决的，过程与方法目标的达成度较好.

4.流程平实，注重层次

具有以下特点：①导——引导学生对问题进行深入思考.如对“函数在区间（1，2）上不单调”和“函数在区间［1，2］上存在单调增区间”两个问题的探究，引导学生借助三次函数的图像，探寻“不单调”与“区间内存在极值点”之间的关系，探寻“区间［1，2］”与“函数的递增区间”之间的关系，将学生的思维引向深处.②启——启发学生用多种方法解决同一问题，拓展学生思维.如在研究2008年江苏高考14题的过程中，启发学生从不同视角出发，用“最值法”“分离参数法”“特殊值法”等方法来求解，体会一题多解，培养学生的发散性思维.③提——提高思维层次，提升思维品质.如在研究2008年江苏高考14题时，在学生用第三种方法“特殊值探路，避免讨论”后，继续追问，能否更进一步，再赋值，从而将特殊值法发挥到极致.④变——通过“一题多变”培养学生思维的深刻性.本节课从母题出发，立足于导数与单调性的关系，纵引横联，一题多变，设计出一系列问题，加深学生对知识的理解，有利于学生思维水平的提升.

5.白壁微瑕，不足尚存

问题3与问题4是学生在本节课中需要突破的两个难点，在引导学生进行辨析时，应留出充足的时间让学生进行独立思考和讨论分析，并通过师生互动的方式深入剖析，使学生充分领会“不单调”及“在某区间上递增”的本质含义，以达成教学目标，但在教学的实施过程中，此处的处理有些仓促，剖析、挖掘得不够深入.H