不可忽视的“定义域”

☉苏州外国语学校 孙龙华

函数贯穿于整个高中数学教学，在函数的定义域、对应法则和值域这三大要素中，定义域是函数的基础，我们在解决函数问题时，应首先考虑函数的定义域.一般而言，函数的定义域并不难求，正因如此，许多学生在解决函数问题时，往往会忽视对函数定义域的求解，从而解错函数问题，而且这种忽略定义域的粗心大意的坏习惯，会给他们今后函数的学习带来很大的隐患.本文结合几类学生错解的函数题目，谈谈定义域在函数问题中的重要性.

一、“判断同一函数”中的定义域

例1判断下列函数是否为同一函数：

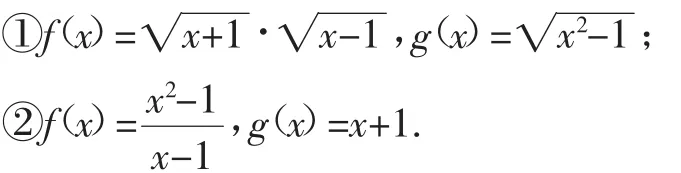
学生错解：①因为所以（fx）与g（x）为同一函数.②因为，所以（fx）与g（x）为同一函数.

错因分析：学生错解过程中忽视了对函数f（x）的定义域的求解，这样在对函数f（x）解析式变形时，没有实施等价转化，导致错解.

解：①因为x+1≥0且x-1≥0，x≥1，所以f（x）的定义域为［1，+∞），又x2-1≥0，所以x≥1或x≤-1，g（x）的定义域为x∈（-∞，-1］∪［1，+∞）.因为f（x）与g（x）定义域不同，故f（x）与g（x）不是同一函数.

②同理，f（x）定义域为（-∞，1）∪（1，+∞），g（x）的定义域为R，定义域不同，故f（x）与g（x）不是同一函数.

点评：判断两个函数是否为同一函数时，必须要对这两个函数的定义域、解析式和值域进行判断，这三个要素都相同的函数，才是同一函数.当然，由于定义域、解析式相同的函数，其值域肯定相同，所以一般我们只需判断函数的定义域和解析式是否相同即可.本例中学生忽视了对定义域的求解，所以误认为是同一函数.

二、“求解析式”中的定义域

例2若，求（fx）的解析式.

学生错解：令，则x=（t-1）2，代入原式有（ft）=（t-1）2+2（t-1），所以f（t）=t2-1，故f（x）=x2-1.

错因分析：换元法是求函数解析式的最基本的方法之一，本题学生采用了换元法来求函数f（x）的解析式，其思路是正确的，但是学生在换元的时候，没有注意到新元的取值范围，即函数f（t）=t2-1的定义域，导致出现了错误.

解法1：（换元法）令，则x=（t-1）2且t≥1，代入原式有f（t）=（t-1）2+2（t-1），其中t≥1，整理得，故

解法2：（配凑法）因为又有，故

点评：我们在求函数解析式时，经常会用到换元法，换元时，一定不能忘记新元的取值范围.因为两个函数即使解析式相同，倘若定义域不同，那么这两个也是不同的函数.

三、“求值域”中的定义域

例3求函数的值域.

学生错解：令，则x=t2+1，故原函数可化为y=t2+1+t，即，所以函数的值域为

错因分析：此题学生的解题思路是正确的，问题出在换元之后的新函数y的定义域上，学生在换元的时候，忽视了新元t的取值范围，这就导致转化之后的新函数y=t2+t+1的定义域错误，从而导致了错误.

解：令则x=t2+1且t≥0，则原函数可化为y=，易知函数y在区间［0，+∞）上为单调增函数，所以当t=0时，函数y有最小值为y=1，所以函数的值域为

点评：函数的定义域决定了函数的值域，所以当我们求函数值域的时候，应首先考虑函数的定义域，而换元法求值域，其本质是利用换元法求函数的解析式，只不过在换元时切不可忘记对新元取值范围的讨论.

四、“判断奇偶性”中的定义域

例4判断函数的奇偶性.

学生错解：因为，所以函数为偶函数.

错因分析：学生对函数奇偶性的定义掌握得不够清晰，偶函数的定义：设函数y=f（x）的定义域为A，如果对任意的x∈A，都有f（-x）=f（x），那么称函数f（x）是偶函数，通过对偶函数定义的分析，我们发现若x∈A，则必有-x∈A，因此偶函数的定义域关于原点对称，这是判断偶函数的前提条件，而这位学生并没有对函数的定义域加以求解，从而导致了错解.

解：因为1-x2≥0且x2-1≥0，所以x∈{1，-1}，f（x）的定义域关于原点对称，此时，函数可化为f（x）=0，满足f（-x）=f（x）=-f（x），故函数f（x）既是奇函数又是偶函数.

点评：由函数奇偶性的定义，我们不难发现，判断一个函数的奇偶性要从两个方面去入手：①定义域是否关于原点对称；②f（-x）与f（x）的关系.另外，求解出定义域之后，要重新考查函数解析式是否可以化简，然后再去判断，万万不能不考虑定义域，而直接去判断f（-x）与f（x）的关系，这样极易带来错误的判断.

五、“单调性”中的定义域

例5求函数y=log2（x2-2x-3）的单调增区间.

学生错解：函数y=log2（x2-2x-3）可以看成由函数y=log2t与t=x2-2x-3复合而成，因为函数t=x2-2x-3在区间（-∞，1）上为单调减函数，在区间（1，+∞）上为单调增函数，且函数y=log2t为定义域上的单调增函数，故根据复合函数的同增异减的原则，原函数y=log2（x2-2x-3）的单调增区间为（1，+∞）.

错因分析：因为函数t=x2-2x-3是嵌入到对数函数y=log2t中的真数位置，故要满足t=x2-2x-3＞0，实际上也就是要先求函数y=log2（x2-2x-3）的定义域，而学生并没有这么做.

解：先求出函数y=log2（x2-2x-3）的定义域，即解不等式x2-2x-3＞0，得到x＜-1或x＞3，所以函数y=log2（x2-2x-3）的定义域为{x|x＜-1或x＞3}，此外，函数y=log2（x2-2x-3）可以看成由函数y=log2t与t=x2-2x-3复合而成，因为函数t=x2-2x-3在区间（-∞，1）上为单调减函数，在区间（1，+∞）上为单调增函数，且函数y=log2t为定义域上的单调增函数，故根据复合函数的同增异减的原则，再结合{x|x＜-1或x＞3}，得原函数y=log2（x2-2x-3）的单调增区间为（3，+∞）.

点评：因为函数的单调区间是函数定义域的子区间，所以求任何一个函数的单调区间时，都需要先求出这个函数的定义域，特别是在求与对数函数复合的复合函数的单调区间时，学生更容易忽视对定义域的考虑，这点必须强调.

六、“解不等式”中的定义域

例6求不等式的解集.

学生错解：因为，所以又因为对数函数为单调递减函数，所以，所以，所以不等式的解集为

错因分析：由于对数函数的定义域为x∈（0，+∞），所以中应有2-x＞0，即x＜2，学生并没有注意到这一限制.

解：因为，所以又因为对数函数为单调递减函数，所以不等式的解集为

点评：求解与对数函数相关的不等式时，不要忘记真数大于0这个限制条件，否则容易造成错解.

函数的三大要素：定义域、对应法则、值域，定义域作为我们研究函数问题时碰到的第一个问题，也是最基础的问题，它直接影响着后续我们对函数解析式、值域以及函数的图像与性质的研究，函数的定义域是解决所有函数问题时都必须优先考虑的先决条件，因此，我们教师要教育学生在学习函数时一定要养成优先考虑函数定义域的习惯，这样才不至于在函数的后续学习中犯有关定义域方面的低级错误，当然，随着函数学习的不断深入，学生一定会有越来越深刻的体会.W