再入飞行器自适应最优姿态控制

张振宁，张 冉，聂文明，李惠峰

(北京航空航天大学宇航学院，北京100191)

0 引 言

航天任务中，姿态控制器的设计是飞行器设计的关键环节之一，其控制性能与任务能否成功密切相关。姿态控制精度、收敛时间、控制量需求是衡量控制性能的主要因素。目前，再入飞行器的姿态控制器设计思路主要有两种。一是线性设计方法，对飞行器原始模型在选定工作点处进行小扰动线性化，采用线性系统理论及增益整定得到全弹道控制器[1]。但再入飞行包线大，速度通常在5马赫以上，存在极强非线性特征，因此在机动过程中采用线性控制器容易产生失稳现象。二是非线性设计方法，它一定程度上体现了模型中的非线性因素，如：反馈线性化方法[2-3]通过严格的状态变化与反馈将非线性系统代数地转化为线性系统，再应用线性系统理论设计控制器，但有相当多的系统无法进行反馈线性化；反步法[3]通过对系统进行多步递推设计，获得较好的全局或局部稳定性，但容易发生微分膨胀现象；滑模法[5-6]以一阶镇定问题取代原高阶跟踪问题，设计过程比较简单且性能很好，文献[7]还用神经网络对估计模型、耦合等扰动进行估计，进一步改善了控制性能，但该方法容易出现控制量的颤振。

近年来，最优控制理论已成为现代控制系统设计的基础理论之一。针对再入飞行器的姿态控制，通过最优控制理论设计控制器可以最大程度优化舵面偏转量、姿态跟踪精度和速度等性能。动态规划作为一种传统的最优控制问题求解方法，由于“维数灾难”导致Hamilton-Jacobian-Bellman(HJB)方程难以直接求解。随着计算技术的不断进步，求解HJB方程的迭代方法得到广泛探索。Werbos[8]首先提出了自适应动态规划(Adaptive dynamic programming，ADP)，建立执行-评价估计结构，并通过值迭代方法求解。Al-Tamimi等[9]证明了这种方法在离散系统上的收敛性。 近几年，Xu等[10]、Lakshmikanth等[11]学者将该方法直接应用于连续系统，但对数据采样时间的苛刻要求导致算法收敛性难以保证，且加重了计算负担。为使连续系统的HJB方程求解更加稳定，基于策略迭代提出的积分型强化学习(Integral reinforcement learning，IRL)算法作为一种新兴算法受到广泛关注[12-13]，该算法采用评价和执行两个网络分别估计值函数和控制策略，并同时更新直到两个网络均收敛到最优。Modares等[14]针对最优跟踪问题，提出了一种非二次型的代价函数，采用IRL算法完成了跟踪控制器的设计；Wang等[15]在Modares等[14]工作的基础上通过修改代价函数设计了鲁棒跟踪控制器； Lee等[16]对IRL算法的收敛性进行了深入研究，并提出了四种衍生算法；Song等[17]通过将Off-Policy与IRL算法结合，大大减弱了控制器对模型的依赖性。以上研究均采用执行-评价双网络结构对HJB方程进行求解，但双网络结构的计算效率和所占用的存储空间不能满足目前再入飞行器姿态控制器的设计要求。

本文提出了单网络积分型强化学习(Single-network integral reinforcement learning, SNIRL)算法，将原评价-执行结构中执行网络的迭代过程用解析式表达，保留评价网络的迭代对值函数进行估计，减少了近一半的计算量和存储空间。该算法的收敛性及闭环系统的稳定性均通过李雅普诺夫稳定性理论得到了证明。

本文的结构如下：第1节构建再入飞行器的最优姿态控制问题；第2节在策略迭代框架下用评价网络估计值函数，采用SNIRL算法求解最优控制问题，设计姿态控制器；第3节给出算法收敛性和系统稳定性证明；第4节进行纵向和横侧向姿态控制仿真。

1 问题描述

从最优控制角度出发，将再入飞行器的姿态控制问题建模为最优控制问题。

参考文献[18]，用于控制器设计的再入飞行器模型为

(1)

式中：α为攻角，β为侧滑角，μ为倾侧角，p为偏航角速率，q为俯仰角速率，q为滚转角速率；g为地球引力加速度，取常值；Ix,Iy,Ixz为转动惯量，也为常值；Z为升力，Y为横向力，L为滚转力矩，N为偏航力矩，M为俯仰力矩，X(·)表示X对(·)的偏导数(例如Mα表示俯仰力矩对攻角的偏导数)。

该模型是在原始模型上进行适当简化后的仿射模型，不包含速度及位置的相关状态，控制量显式出现在方程中，可简写为

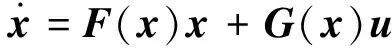
(2)

式中：x∈Rn为状态量，u∈Rm为控制输入；F(x)∈Rn,G(x)∈Rn×m是只与x相关的非线性函数。

最优控制策略可以通过最小化某个人为选择的代价函数V(在ADP中也称为值函数)得到，V的形式为

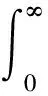
(3)

式中：

r(x,u)=Q(x)+uTRu

(4)

最优控制问题描述为：对于由方程组(2)定义的系统，寻找最优控制策略u*，最小化代价函数(3)。

容许控制[19]定义为：若F+Gu在集合Ω∈RN上连续，μ在Ω上连续且μ(0)=0，若μ在Ω上镇定系统(2)且对∀x0∈Ω,V(x0)有界，则称μ容许控制，记作μ∈Ψ(Ω)。

对μ∈Ψ(Ω)，可以将式(3)转化为极小形式，它是一个李雅普诺夫方程

(5)

式中：Vx表示V对x的偏导。

这个无限时间最优控制问题的哈密顿方程为

(6)

根据极大值原理，最优控制μ*可通过最小化式(6)得到。实际上对形如式(2)的系统，对式(6)应用驻点条件，能得到最优控制策略与最优代价函数的关系，为

(7)

(8)

2 自适应最优姿态控制器设计

将策略迭代作为算法框架，保证迭代计算结果向最优控制律收敛；设计评价网络，在迭代计算中估计值函数；最后提出SNIRL算法使估计值向最优值收敛，完成求解，得到自适应最优控制器。

2.1 策略迭代

策略迭代是利用强化学习求解最优控制问题的一种迭代方法。具体过程为：

(1)确定当前控制策略下的值函数

(9)

(2)求解最小化哈密顿方程的控制策略，并对当前控制策略进行更新

(10)

事实上，对系统(2)，通过式(10)可以解析得到

(11)

(3)在步骤(1)和步骤(2)之间不断迭代直至收敛。

当初始控制策略为容许控制时，该算法过程中的每次迭代都会使得控制策略向更优的方向收敛，并最终收敛到最优控制策略u*(x)以及相应的最优代价函数V*(x)。该算法的收敛性在早年文献中已有证明[21]。

针对由式(2)～式(3)构成的最优控制问题，策略迭代过程包括依据式(5)进行策略评价(即确定值函数)，以及依据式(7)进行策略更新。

2.2 评价网络设计

从第1节的分析可以看出，控制策略对应的值函数难以求解，导致策略迭代过程的步骤1无法实现，故设计评价网络估计值函数。

选取Φ(x)=[φ1(x),φ2(x),…,φN(x)]T保证φ1(x),φ2(x),…,φN(x)互相独立，并对Φ(x)各元素加权达到估计值函数的目的，该估计结构被称为评价网络，其表达式为

V=WTΦ(x)+ε

式中：W∈RN为网络权重,Φ(x):Rn→RN为激励函数,ε为估计误差。

在上述估计结构下，值函数V对状态量x的偏导为

(12)

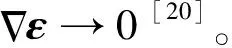
在计算过程中，由于W为未知量，故采用其估计量来推动迭代运行

(13)

2.3 基于单网络积分型强化学习的控制器设计

将网络当前输出与期望输出之间的差异描述为误差函数

(14)

迭代过程中采用式(13)估计值函数后，误差函数为

(15)

采用梯度下降法调整网络权重最小化Δ，从而使网络输出向期望输出收敛，首先定义最小方差形式代价函数

(16)

(17)

为增强梯度下降法在求解多维方程组时的性能，借鉴Levenberg-Marquardt算法在式(17)中加入归一化处理项得到

(18)

式中：a∈R+为学习速率，

(19)

在IRL算法中，用于估计控制策略的执行网络结构为

(20)

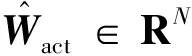
Vamvoudakis等[13]和Zhang等[15]提出了一种“非标准形式的更新律”来更新执行网络。在文献[13]中，这一更新律为

式中：aact是学习速率，为常值；ms=(T最后一项是为李雅普诺夫稳定性证明增加的量。

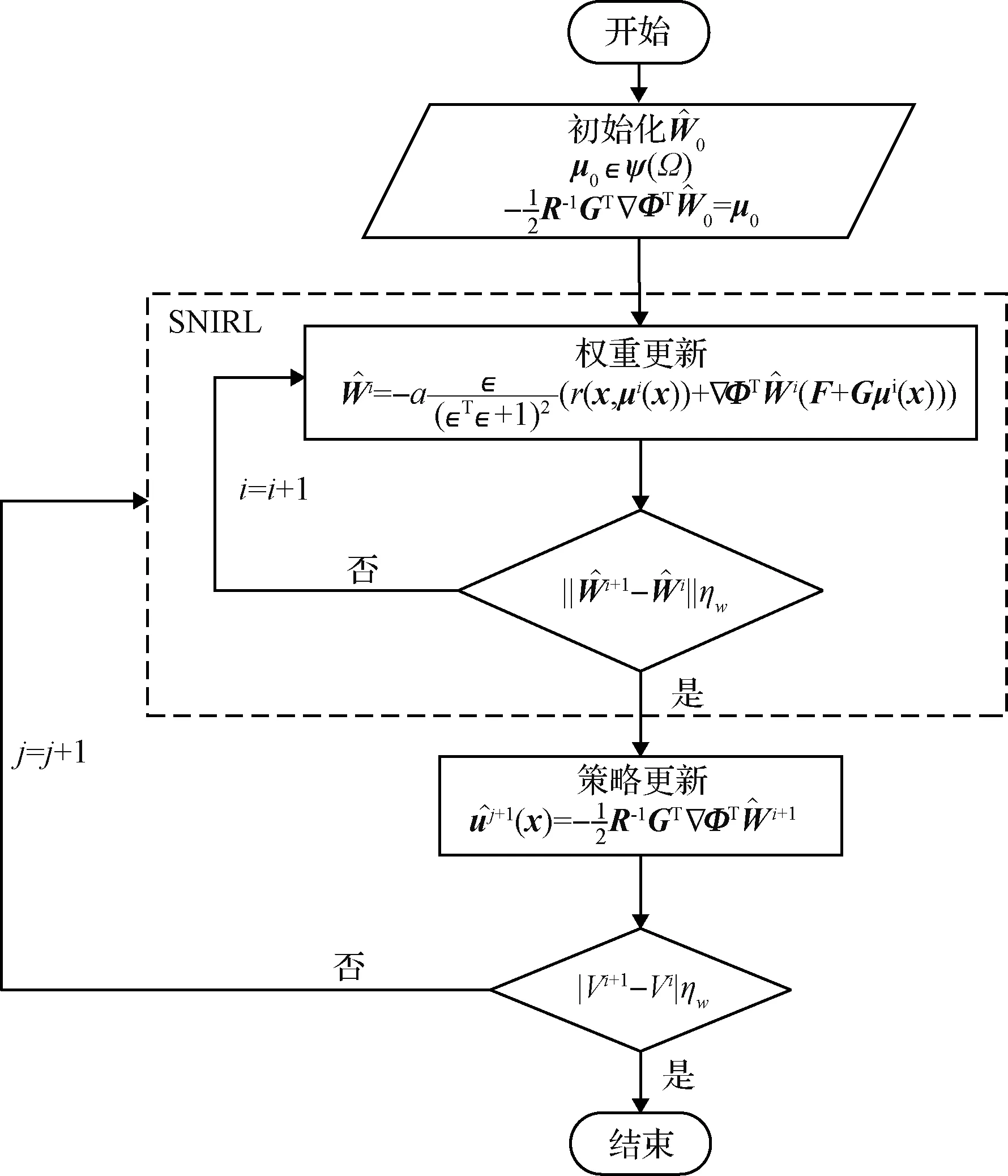
图1 算法流程Fig.1 Algorithm progress

基于以上猜想，提出SNIRL算法，下面给出整个算法流程。

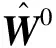
(21)

求解。

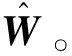
(3)相应的控制策略的计算式为

(22)

SNIRL算法将IRL算法中执行网络的迭代过程替换为解析式(22)，单网络的设计使得算法结构更加简洁。该算法使初始给出的容许控制在迭代过程中逐步收敛到最优控制策略。

整个控制系统的结构如图1所示。图中xcmd为指令信号；自适应最优控制策略记为uN，通过SNIRL求解最优控制问题获得；前馈网络是一个神经网络，作用是对飞行器配平点进行拟合，给出前馈控制量uF。总控制策略为

utotal=uN+uF

(23)

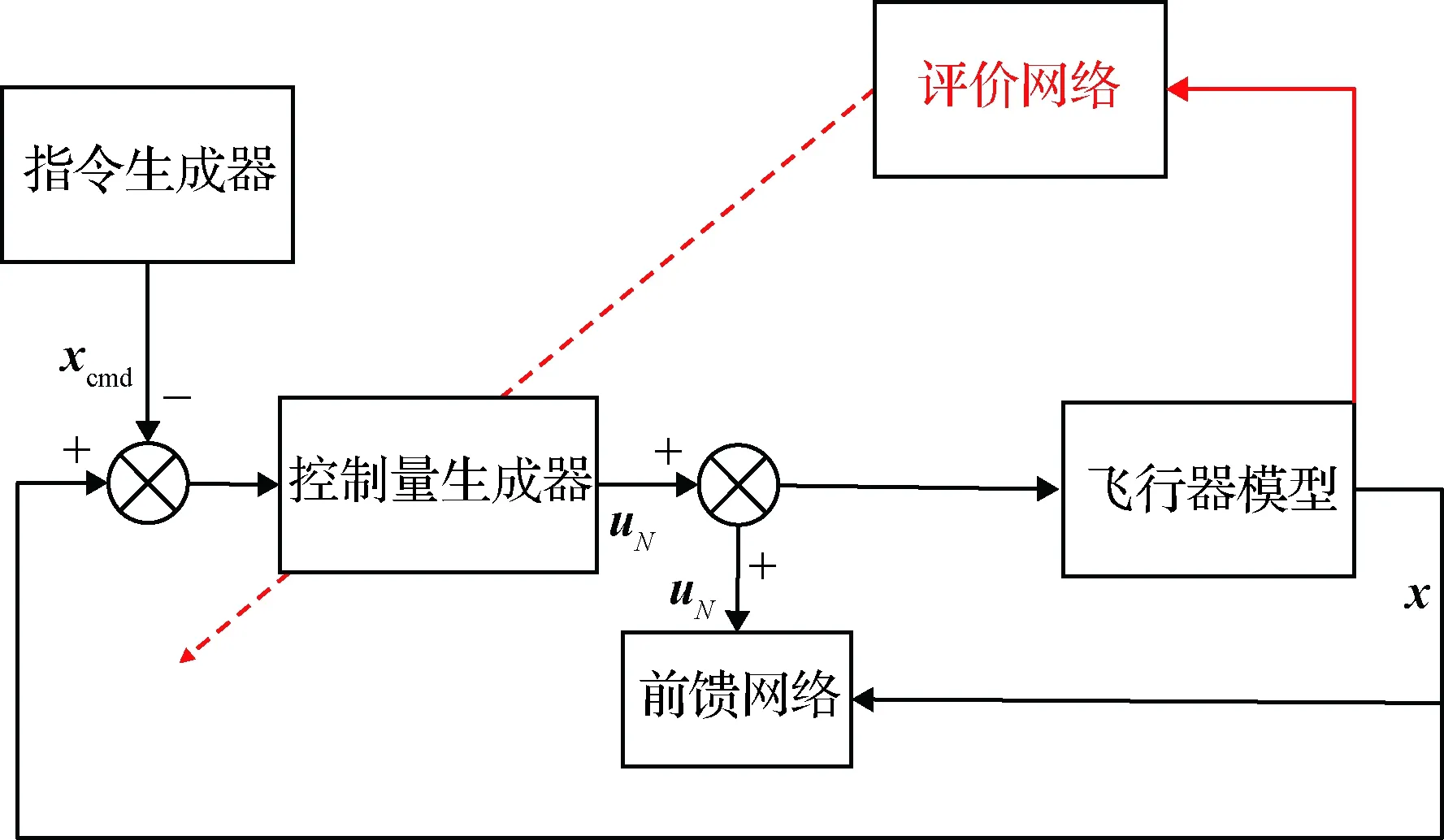
图2 控制系统结构图Fig.2 Control system structure

3 性能分析

下面进行算法的收敛性分析。

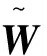
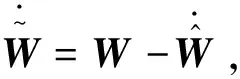
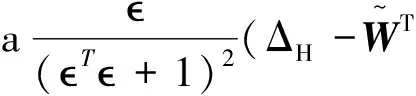
取李雅普诺夫候选函数

记ξ=(T+1)2,L的导数为

由柯西不等式：

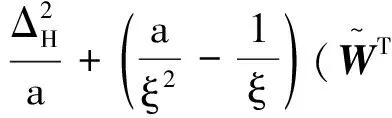
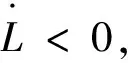
由于实数具有稠密性，∃κ，使

因此只要

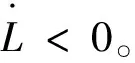
为了增强参数调节的灵活性，在实际应用时，学习速率取

a=diag(a1,a2,a3,…,aN)

(24)

式中:a1,a2,…,aN∈R+,为常值。

下面在代价函数为二次型，即C=xTQx+uTRu时，给出闭环系统稳定性分析。

定理2. 对系统(2)，当网络更新律为式(18)，控制律由式(22)计算时，存在时间T，使得x(t)一致最终有界。且

式中：η>0,λmin(Q)为矩阵Q的最小特征值。

证. 考虑指令信号xcmd，记z=x-xcmd，有：

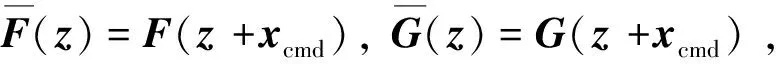
(25)

由式(8)得

(26)

对V(z)沿式(25)取时间导数，有

(27)

代入式(26)，得

(28)

将式(22)代入式(28)，得

考虑到R正定，有

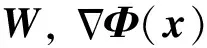
则η有界且

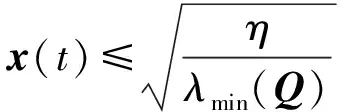
4 仿真校验

本节以X33为对象，分纵向和横侧向对自适应最优姿态控制器进行仿真校验。在纵向姿态仿真中与IRL算法进行对比，验证SNIRL可以提升收敛速度和计算效率，节省存储空间；同时在两种仿真中均以相同的Q,R矩阵设计传统的LQR控制器作为对比，对自适应最优控制器的有效性进行校验。

4.1 纵向姿态控制

在高度h=45.09 km，速度v=3748 m/s,α=10°的工况下，给出机动指令αcmd=13°。

值函数由式(3)确定，式中：

权重记为

激励函数φ定义为

故有

初始权重为

图2给出了SNIRL算法及双网络的IRL算法的权重收敛过程图。图中Wcritic和Wactor分别为IRL算法的评价网络权重和执行网络权重，W为SNIRL算法的评价网络权重。两种算法的权重均最终收敛到

图3为两种算法的权重收敛过程图，下表为对两种算法的计算时间、存储占用、收敛时间的统计：

表1 SNIRL与IRL算法对比Table 1 Comparison of SNIRL and IRL

在迭代过程中，两种算法的W1均几乎没有变化，这是由于W1在式(22)的计算中没有贡献，故算法不会对该值进行自适应学习，是合理的结果。

那么可以得到

总控制策略由式(24)计算。

控制结果在图4中展示。LQR控制器的仿真结果也在图中作为对比绘出。

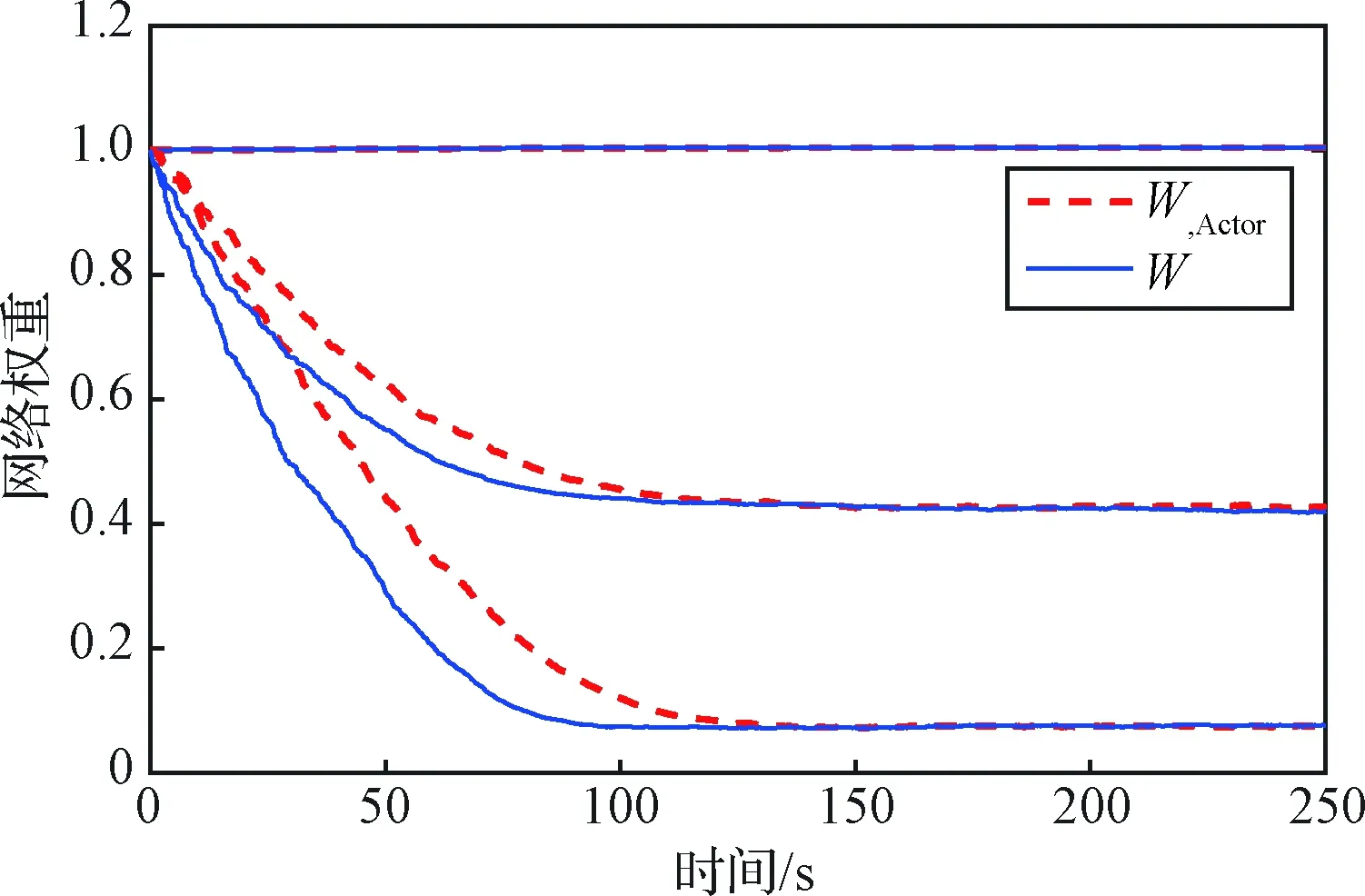
图3 SNIRL和IRL算法的收敛过程Fig.3 Convergence of IRL and SNIRL algorithm

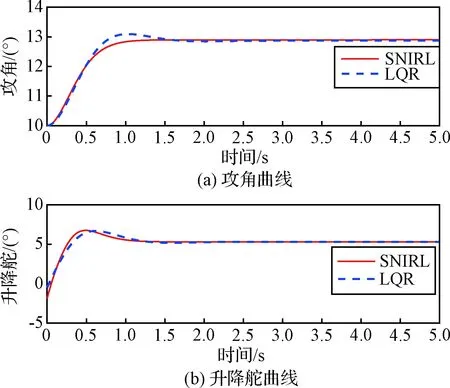
图4 状态量和控制量曲线Fig.4 State and control versus time

从图3可以看出，SNIRL算法能够收敛到最优解，且相比IRL算法，由于SNIRL算法在迭代过程中将执行网络逐渐更新的过程代替为解析式，消除了滞后的执行网络的收敛过程，故在每一次迭代中，权重都可以更快地收敛，因而总的收敛时间有所减少；从表1可以看出，SNIRL比IRL算法收敛更快，计算效率提高了近一倍。同时又由于SNIRL算法不需要存储执行网络的权重数据，故相比IRL算法可以节省近一半的存储空间。

从图4可以看出，自适应最优控制器完成了姿态跟踪任务。且由于该控制器的设计是以非线性模型的最优控制理论为基础进行的，对比LQR控制器稳态误差更小，快速性也更好。

4.2 横侧向姿态控制

在高度h=45.09 km，速度v=3748 m/s,β=0.1293°,μ=-65.9°的工况下，给出机动指令βcmd=0°,μcmd=-68°。

值函数由式(3)确定，式中：

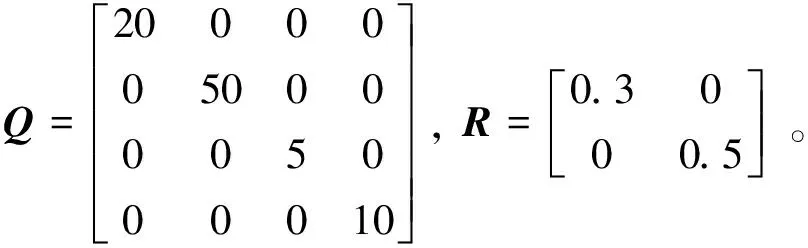
激励函数φ定义为

φ(x)=[β2βμβpβrμ2μpμrp2prr2]T

权重记为

W=[W1W2W3W4W5W6W7W8W9W10]T

本节同样对两种算法进行了对比,仿真结果如图5、图6所示。表2进一步验证了SNIRL算法能够提高计算效率和节省存储空间。

从图5可以看出，在横侧向姿态控制中，自适应最优控制器相比LQR控制器表现出了更好的快速性和更小的稳态误差。图6为控制量随时间的变化曲线，可以看到LQR控制器所给出的控制量存在震荡，而自适应最优控制器的控制策略则更加平滑，这是自适应最优控制器更好地满足了性能指标要求的体现。

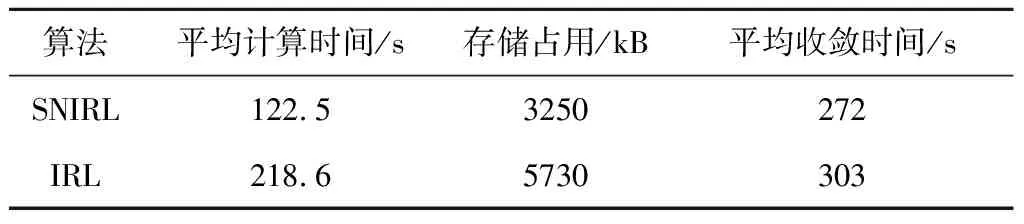
表2 SNIRL与IRL算法对比Table 2 Comparison of SNIRL and IRL

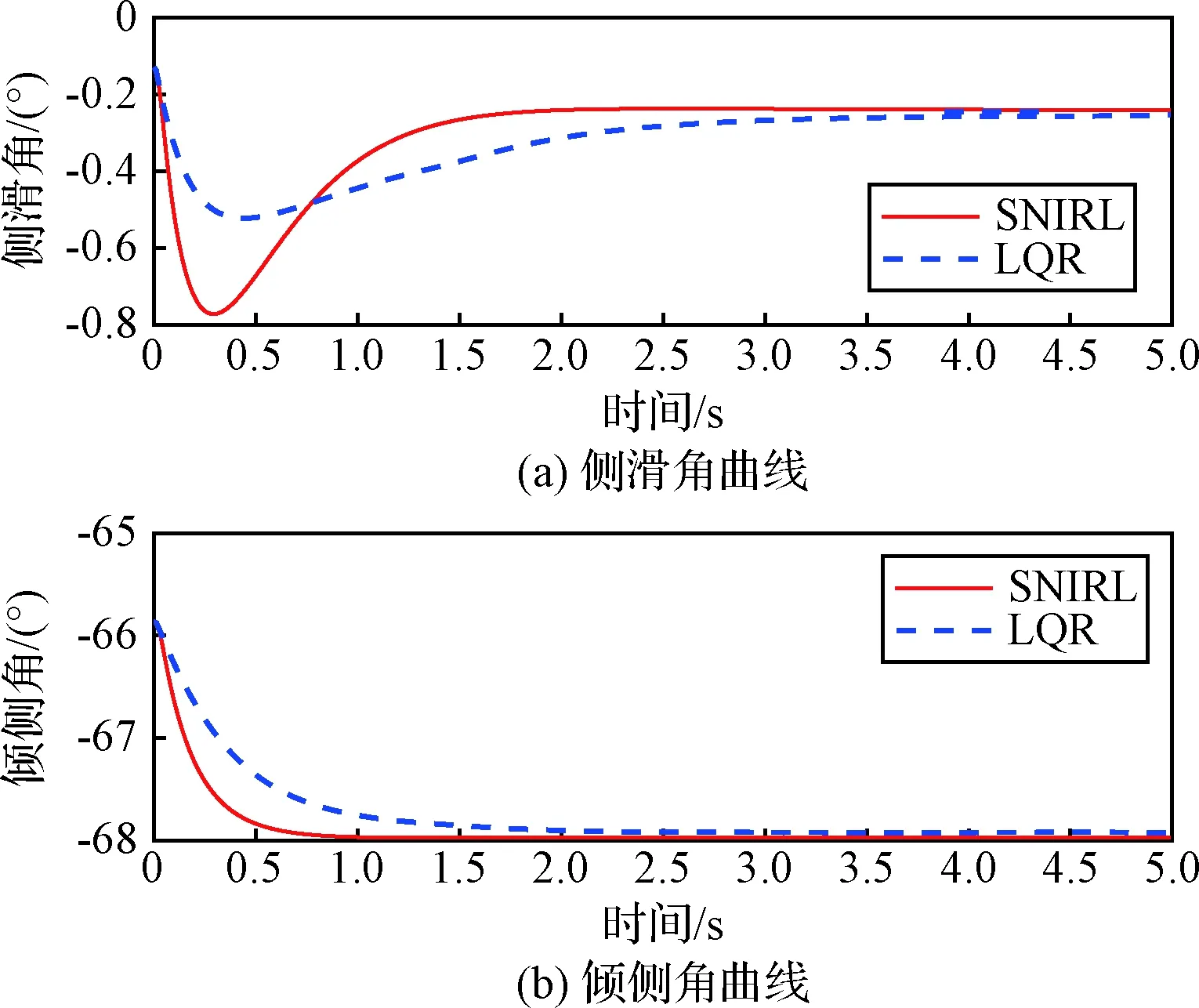
图5 状态量曲线Fig.5 State versus time

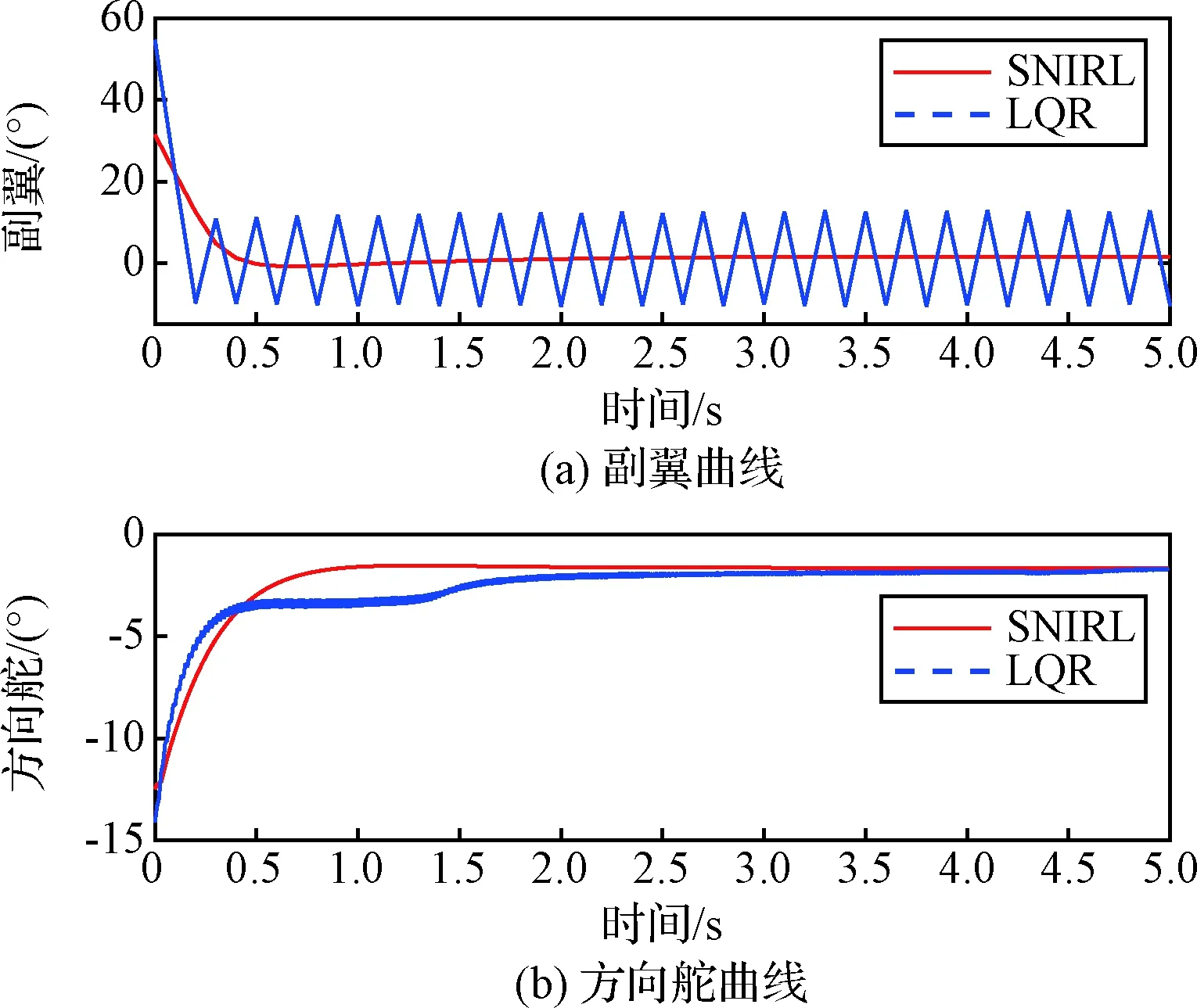
图6 控制量曲线Fig.6 Control versus time

5 结 论

针对再入飞行器姿态控制问题，通过估计值函数，采用基于策略迭代的单网络积分型强化学习算法，设计了自适应最优控制器。在求解最优控制问题时，改进了IRL算法，省去了执行网络，并将其迭代计算过程用解析式代替，使算法结构更加简洁，计算效率更高。在性能分析中通过李雅普诺夫稳定性理论证明了SNIRL算法的收敛性及闭环系统的稳定性。仿真结果表明， SNIRL算法相比IRL算法节省了近一半的计算量和存储量，且收敛速度更快；所得到的自适应最优控制器具有良好的性能。