行星着陆动力下降段相对视觉导航方法
2019-03-14朱圣英崔平远栾恩杰
秦 同,朱圣英,崔平远,栾恩杰,2
(1. 北京理工大学宇航学院,北京 100081;2. 国家国防科技工业局,北京 100048)
0 引 言
动力下降段是行星着陆的最终阶段,直接决定了最终的着陆精度。为实现精确着陆,着陆器在该阶段需通过自主导航实现高精度姿轨估计,并以此为基础实施制导控制,到达预定着陆点[1]。光学导航相机观测量中同时包含了着陆器的位置与姿态信息,且视觉导航自主性强,技术成熟,是实现动力下降段着陆器姿轨估计的有效途径[2]。
对行星着陆视觉导航的研究主要分为三类。第一类为绝对视觉导航。相机提取大型自然路标,通过与行星地形数据库匹配获得路标在行星固连坐标系下的位置,以此为导航参考估计着陆器的状态[3-4]。该方法可以获得着陆器在固连坐标系下的绝对位置、速度及姿态信息。然而,由于在行星着陆动力下降段,着陆器高度较低,相机视场受限,着陆区域通常又选在自然路标匮乏的大范围平坦区[5],因此难以观测到可用的自然路标。且行星全局地形数据库本身存在一定的误差,影响了导航系统精度[6]。
第二类为相对位姿估计。光学相机只需提取图像中的随机特征点,通过序列图像中特征点匹配,估计着陆器的位置及姿态变化,进而获得着陆器的速度与角速度信息[7-8]。该方法不依赖地形数据库,随机特征点可以为陨石坑、岩石等,数量充足。然而该方法无法获得着陆器相对着陆点的状态信息,不能满足定点着陆的要求。
第三类为相对着陆点的视觉导航。着陆器通过相机跟踪预定着陆点或在线选取着陆点[9],并提取着陆点周围随机特征点,利用随机特征点像素坐标估计着陆器相对着陆点的状态,实现定点着陆[10-12]。该方法既有充足的特征点做导航参考,又可实现相对着陆点的状态估计,满足行星精确软着陆的需求。本文的研究即属于此类视觉导航方法。
在实现相对视觉导航时,由于单一相机无法获得景深信息,因此需其他辅助敏感器。文献[12]通过双目视觉相机实现了相对导航,获得了着陆器的全状态高精度估计。然而双目相机的应用受可视区域、多特征点可分辨率约束以及视差可分辨率约束,且图像处理过程较单目相机复杂,实时性较差。文献[11]研究了利用三波束雷达测量辅助的相对视觉导航方法,该方法虽然可估计出着陆器的位置和速度信息,但未能充分利用观测信息,无法估计出着陆器的全部姿态。
本文研究基于单目相机与三波束雷达的相对视觉导航方法,以实现着陆器全状态估计。本文提出的方法利用相机和雷达的测量信息构建相对导航坐标系并求解随机视觉特征点在该坐标系下的位置矢量,利用求解得到的特征点为参考,设计导航系统,估计着陆器在相对导航坐标系下的位置、速度及姿态信息。同时,对导航系统进行可观测度分析,通过构建可观测度矩阵,解耦分析位置和姿态的可观测性,获得满足全状态可观的最少特征点数量及位置要求。最后通过仿真分析着陆器状态误差,验证可观测度理论分析及导航性能。
1 相对导航方案
本节首先给出光学导航相机与三波束雷达的观测模型,然后利用两者的观测量构建相对导航坐标系,再结合动力下降段着陆器姿轨耦合动力学方程设计相对导航系统。
1.1 敏感器观测模型
不失一般性,将导航相机假设为针孔相机模型,在动力下降段,相机跟踪拍摄着陆点及其周围地形的图像,或者通过相机图像在线选择着陆点,提取着陆点及图像中的光学特征点,其中着陆点为光学特征点之一。光学观测原理如图1所示。图中,oc-xcyczc表示相机坐标系,f为相机焦距,(p,l)为目标点在像平面上的像素点坐标。
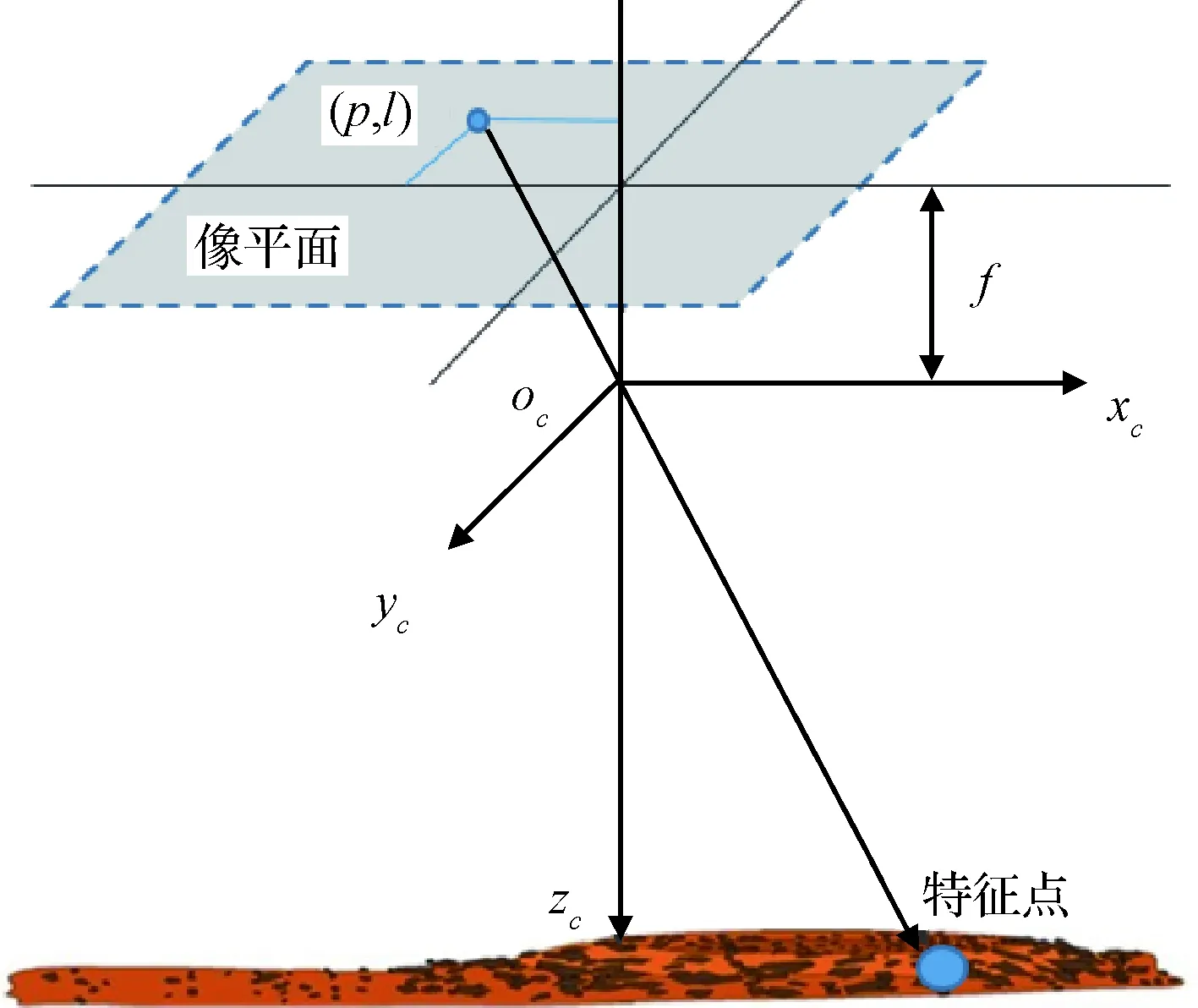
图1 光学导航原理示意图Fig.1 The geometric schematic of optical navigation
光学相机的观测模型如式(1)所示。
(1)
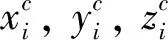
(2)
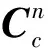
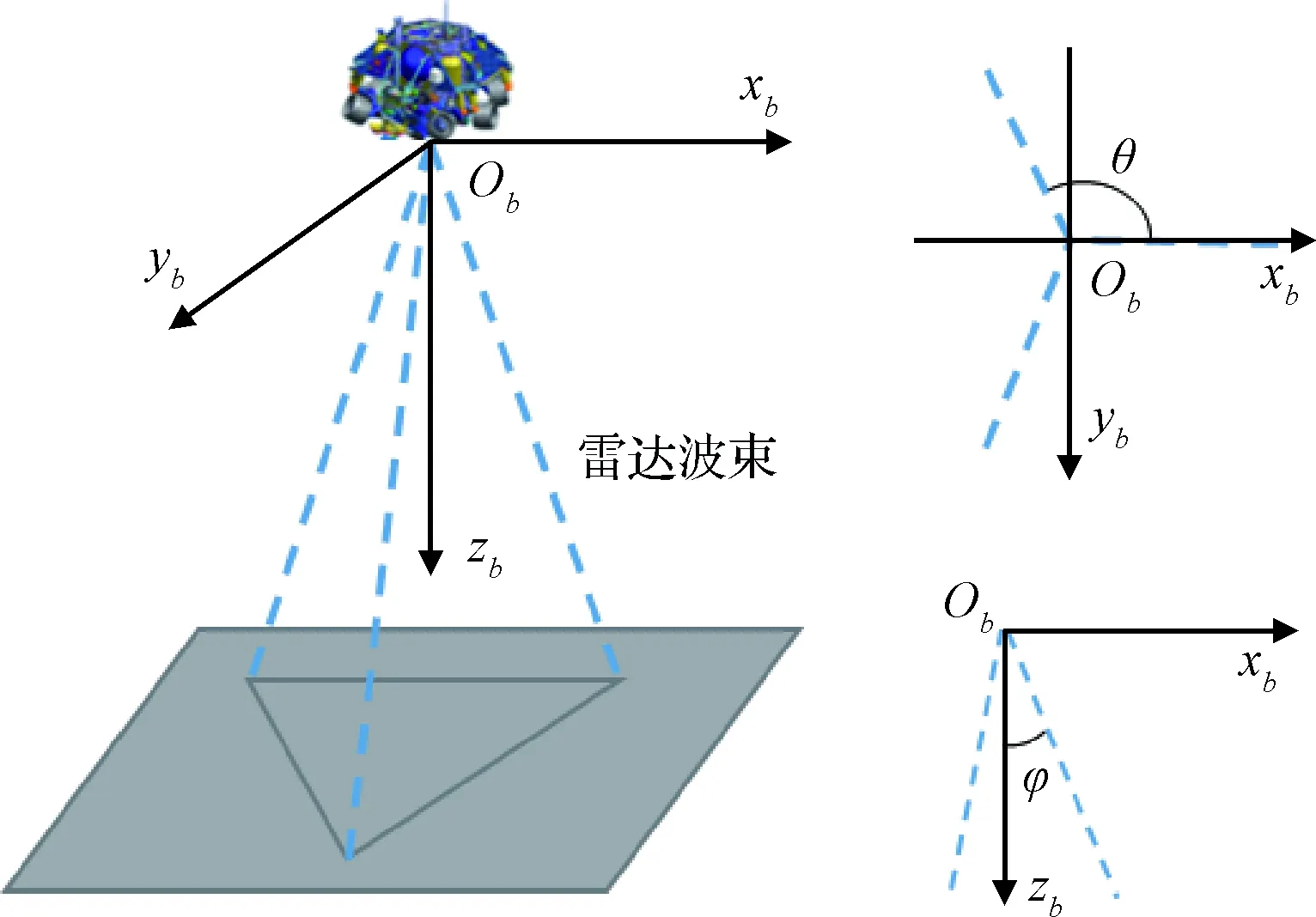
图2 三波束雷达几何示意图Fig.2 The geometric schematic of the three-beam radar
除光学导航相机外,着陆器一般载有多波束雷达,可实现多方向激光测距,考虑文献[13]中的多波束雷达,如图2所示。图中,ob-xbybzb为着陆器本体坐标系,三波束在obxbyb内均匀分布,夹角θ=120°,其中一条波束在obxbyb平面内的投影沿xb轴方向;每一条波束与本体系Z轴的夹角均为φ=30°。雷达可测量着陆器沿波束方向到火星表面的距离,根据着陆区平面假设,观测模型如式(3)所示。
(3)
(4)
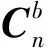
(5)
(6)
(7)
1.2 相对导航坐标系
由于动力下降段着陆器高度较低,相机视场范围较窄,且着陆区域一般在大范围平坦区,相机观测到的光学特征点一般为岩石等尺度较小的地形特征,而难以观测到火星地形数据库中已有的地形特征。因此无法获得特征点在火星全局坐标系下的位置。本小节将基于光学特征点建立相对导航坐标系,并利用相机与雷达的观测量计算特征点在相对导航坐标系下的位置,将此位置作为着陆器在相对导航坐标系下的导航基准。
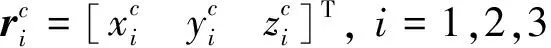
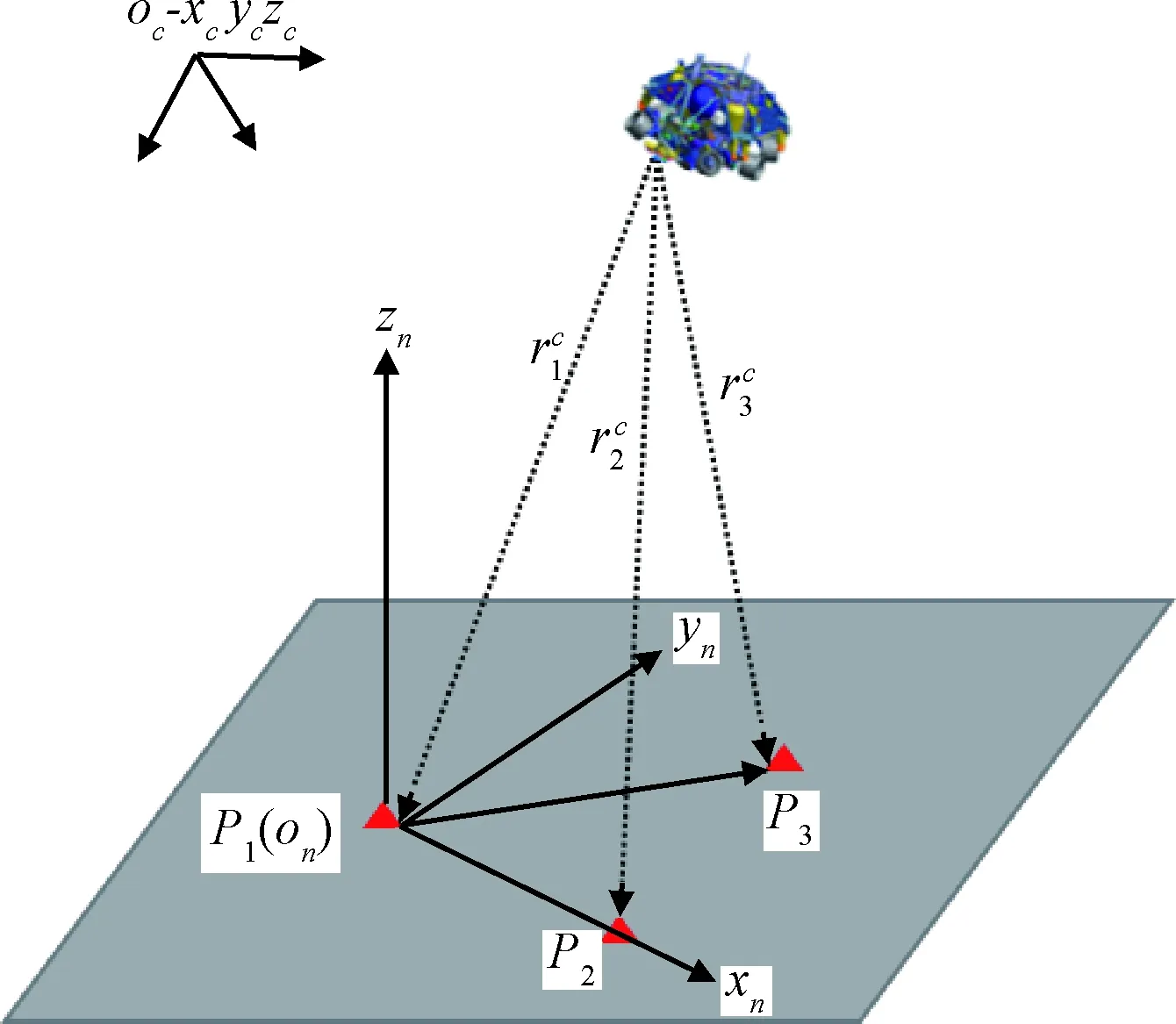
图3 相对导航坐标系Fig.3 The relative navigation reference frame
在相对导航坐标系内进行导航,需获取特征点在该坐标系下的位置信息。根据导航相机的观测量可获得特征点在本体系下的单位方向矢量,如式(8)所示。
(8)
结合三波束雷达的测距信息及雷达安装方向信息可得到本体系下波束照射点相对着陆器的三维位置矢量,如式(9)所示。
(9)
假设着陆区域近似为平面,则根据式(9)可得到本体下的着陆平面单位法向量,如式(10)所示。
(10)
结合式(8)与式(10),可得到特征点在本体系下的三维位置矢量,如式(11)所示。
(11)
由此可构建相对导航坐标系的三个特征点之间的位置矢量为:
(12)
(13)
易得到on-xnynzn三轴在本体系下的单位矢量为:
(14)
(15)
ey=ez×ex
(16)
则导航坐标系到本体坐标系的旋转矩阵为:
(17)
特征点在导航坐标系下的三维位置矢量如式(18)所示。
(18)
至此便得到相对导航坐标系下的导航参考基准位置。
1.3 相对导航系统
相对导航系统需估计着陆器相对目标点的位置、速度以及在相对导航坐标系下的姿态信息。给定导航状态矢量如式(19)所示。
(19)
式中,r,v,q分别为探测的位置、速度及姿态四元数。相对导航坐标系并非严格意义上的导航坐标系,然而在着陆动力下降段,由行星转动产生的科氏加速度远小于行星引力加速度及控制加速度,因此可将其忽略,将相对导航坐标系近似为惯性坐标系,则着陆器的轨道动力学及姿态运动学方程如式(20)所示。
(20)
式中,ac为本体系下的控制加速度,g为行星重力加速度矢量,ω为姿态角速度,Ω(ω)为四元数运动学矩阵,如式(21)所示。
(21)
式中,ωx,ωy,ωz为ω的三轴分量。根据着陆器的动力学方程可得导航系统状态方程如式(22)所示。
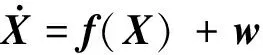
(22)
式中,w为系统噪声,在此假设为高斯白噪声。
导航系统的观测量为特征点在相机坐标系下的三维位置矢量,观测方程如式(23)所示。
(23)
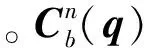
(24)
式中,q0为姿态四元数的标量部分,q1,q2,q3为姿态四元数的矢量部分。
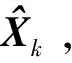
(25)
式中,下标表示时刻,Qk表示系统噪声协方差阵,Rk表示测量噪声协方差阵,为对称正定矩阵,δkj表示Kronecker函数。tk时刻的状态可通过状态预测与观测更新得到。具体过程如下:
一步预测:
(26)
(27)
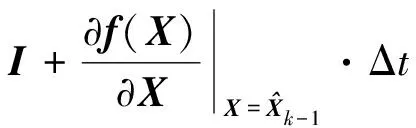
(28)
观测更新:
(29)
(30)
(31)
(32)
相对导航流程如图4所示。需注意,本文的导航方法使用的观测量并非相机与雷达的原始观测量,而是根据原始观测量计算得到的特征点在本体系下的三维位置矢量。滤波器中采用的观测方程,即式(23)中用到的特征点位置矢量也是通过原始测量计算得到的,计算公式即为式(18)。
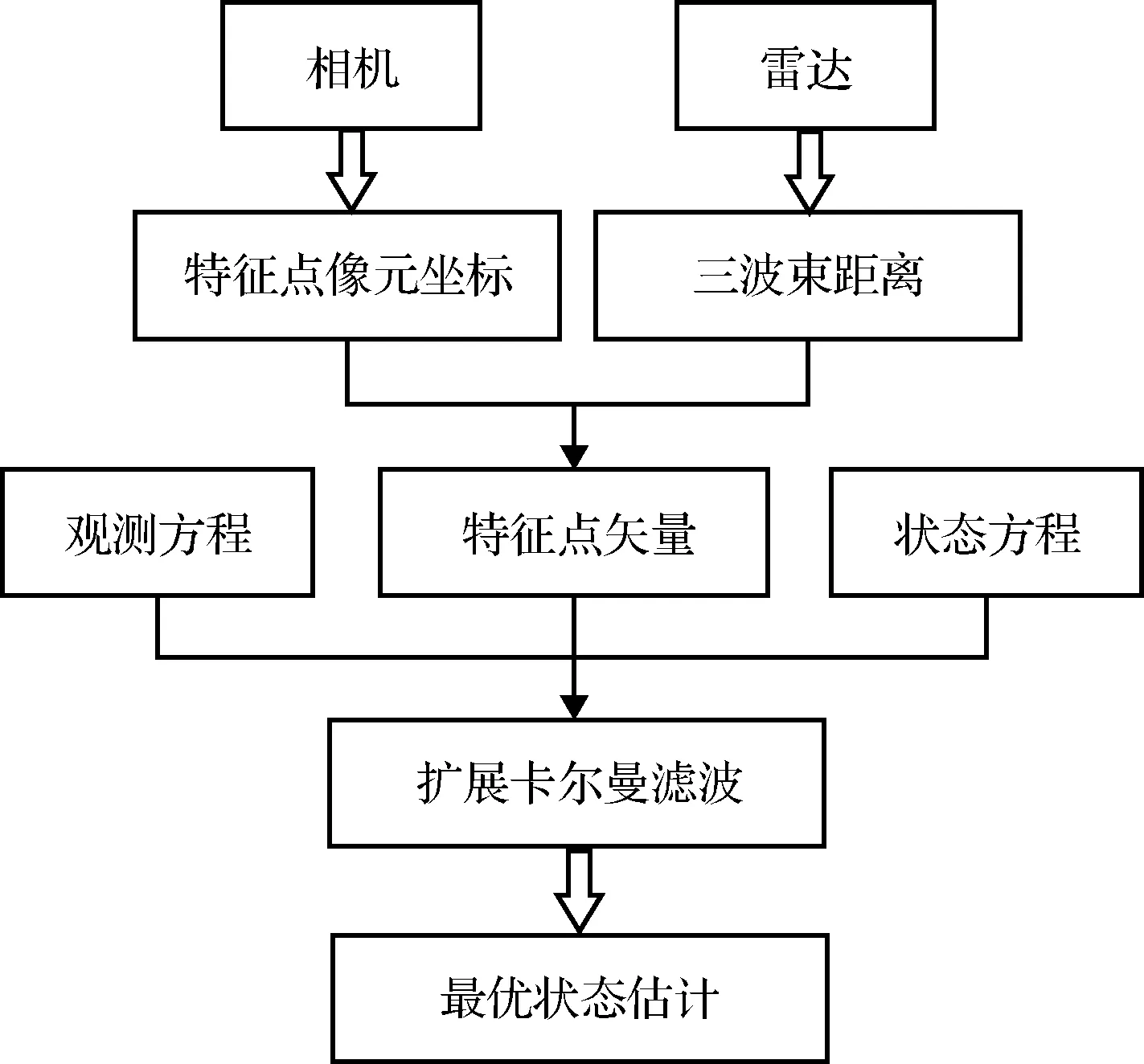
图4 相对导航流程Fig.4 The operation sequence of relative navigation
2 可观测度分析
在第1节构建的导航系统中,相机视场中的特征点数量及位置是影响导航性能的关键因素。本节从导航可观性的角度对导航系统进行理论分析,通过构建可观测度矩阵,解耦分析着陆器位置及姿态的可观测性与特征点数量及位置的关系,解析获得满足着陆器全状态可观的基本条件。
2.1 位置可观性
对于式(22)~式(23)构成的非线性系统,可通过线性化求解雅克比矩阵,进而构建可观测度矩阵。在tk时刻,状态方程的雅克比矩阵具体形式如式(33)所示。
(33)

(34)
观测方程雅克比矩阵形式如式(35)所示。
(35)
式中,
(36)
通过线性化矩阵得到的系统可观测度矩阵一般形式如式(37)所示。
(37)
式中,n为系统状态维数。
将式(33)与式(35)代入式(37)可得导航系统可观测度矩阵,取式(37)的前两项得:
(38)
本小节只分析着陆器位置和速度的可观性,根据可观测度矩阵的性质,前6列的线性关系对应了着陆器位置和速度的可观测度。在状态方程中,姿态与位置的耦合体现在速度微分方程中,A3×4正是由于这种耦合关系产生的,而在构建式(38)所示的可观性矩阵时将A3×4消掉,因此可以解耦分析位置和速度的可观性。在本小节中,假设姿态可观,忽略可观测度矩阵中与姿态相关的后四列,取式(38)前六列作为位置速度的可观测度矩阵,如式(39)所示。
(39)
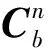
(40)
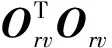
(41)
式(41)的所有特征值均为N,因此位置速度可观测度始终为1,且与特征点数量无关。
2.2 姿态可观性
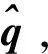
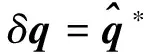
(42)
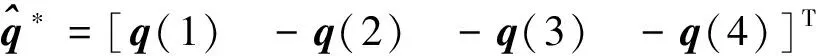
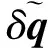
(43)
式中:
(44)
定义观测误差如式(45)所示。
(45)
式中:Yi表示针对第i个特征点的观测量。将观测误差方程线性化可得:
(46)
(47)
通过式(47)可分析观测量中的姿态信息。记观测信息矩阵为:
(48)
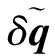
(xi-x)Q(1)+(yi-y)Q(2)+(zi-z)Q(3)=0
(49)
可知观测量中不包含着陆器姿态在导航坐标系下沿ri-r方向的旋转信息。
当观测两个特征点时,可得观测信息矩阵为:
(50)

(51)
式(50)满秩的充要条件为
(52)
式(52)要求:
(r2-r)≠k(r1-r)
(53)
式中,k为比例因子。通过上述分析可知:观测两个特征点,且两个特征点相对着陆器的视线矢量不共线时,观测量中包含了着陆器的三轴姿态信息。同理,当着陆器观测三个及以上不同的特征点时,观测信息中也包含完整的三轴姿态信息。
通过上述分析可知某一观测时刻观测量中包含的姿态信息,对于观测2个及以上不同特征点的情况,由于各个时刻的观测量中都包含了三轴姿态信息,因此通过序列观测可以准确估计出姿态。当观测一个特征点时,通过式(49)可知,每个时刻的观测量都缺少了着陆器姿态沿某个方向的旋转信息。由于在动力下降过程中,着陆器的姿态及特征点相对着陆器的位置矢量不断变化,因此需要分析导航系统通过序列观测获得着陆器姿态的能力。
为分析在序列观测量及状态方程作用下的导航系统可观性,需构建分段线性定常系统可观测度矩阵。对于式(43)所示的微分方程,其离散化状态方程如式(54)所示。
(54)
式中,Φk,k-1为tk-1时刻到tk时刻的状态转移矩阵。根据文献[14]可知,状态转移矩阵具有如下形式:
(55)
式中,Δq为tk-1时刻到tk时刻的四元数变化。综合t0到tk时刻的观测量,得到姿态可观测度矩阵如式(56)所示。
(56)
(57)
在动力下降过程中,若特征点相对着陆器的位置矢量发生变化,或着陆器存在姿态运动,着陆器相当于观测了不同的特征点,可观测度矩阵Oa满秩。因此从序列观测的角度出发,着陆器只观测一个特征点也可实现姿态可观。具体的分析将在下一节中通过数学仿真分析。
在2.1节中分析位置速度可观性时假设姿态可观,并得到了一个特征点就可式位置速度可观测结论,而姿态的可观性分析证明了仅有一个特征点时姿态可观,因此综合2.1节与2.2节的分析可知,当仅有一个特征点可用时,相对导航系统完全可观。
3 仿真校验
本节通过数学仿真校验相对导航系统可观性以及相对导航可行性,并结合姿态和轨迹制导分析着陆器通过相对导航实现定点着陆的能力。
3.1 仿真参数设置
着陆器在相对导航坐标系下的初始标称状态及状态标准差如表1所示,姿态四元数可根据初始姿态欧拉角计算得到[15]。导航敏感器参数如表2所示。
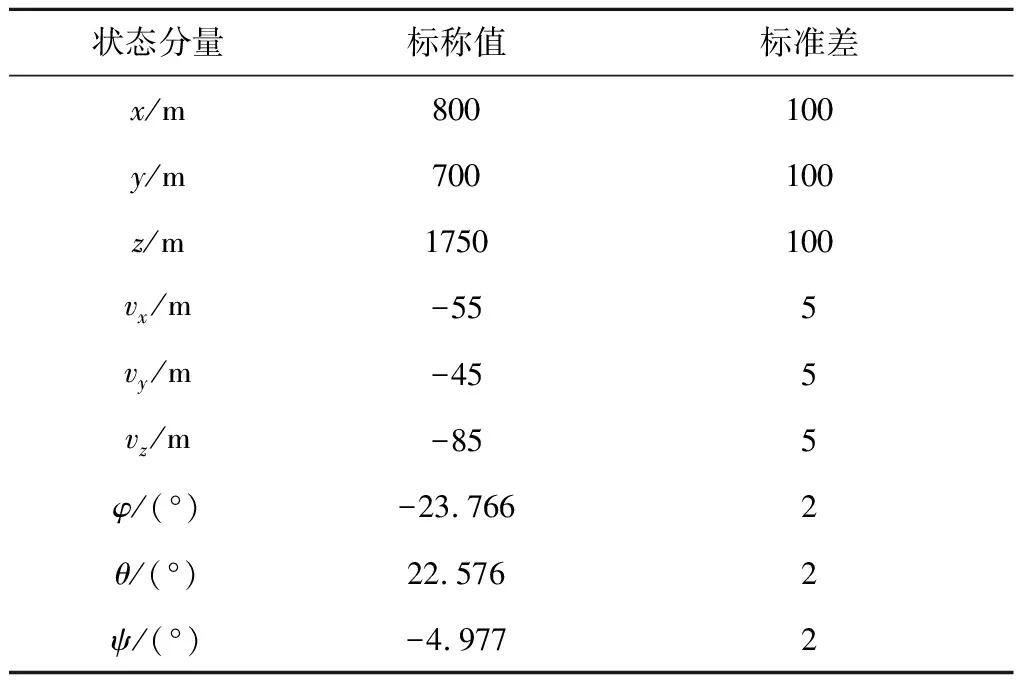
表1 初始标称状态及状态标准差Table 1 Nominal values and standard deviations of initial states
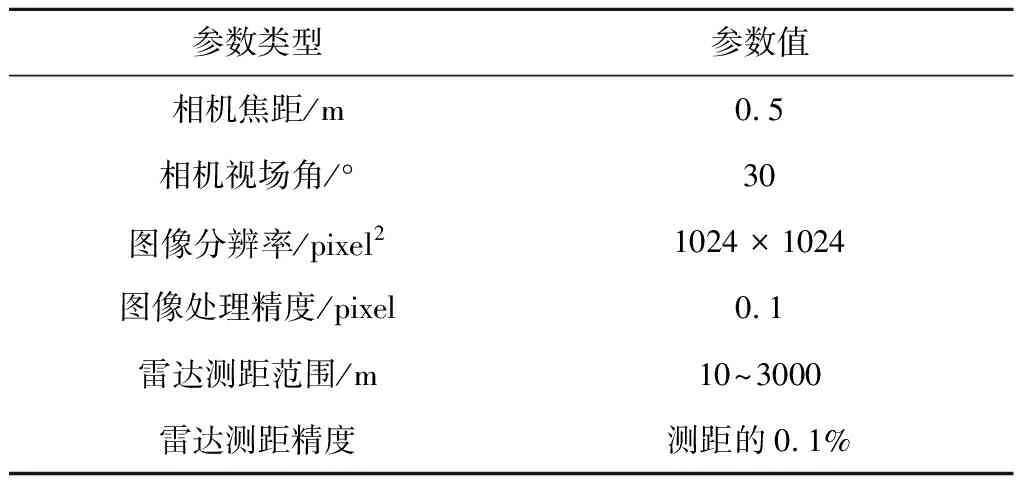
表2 导航敏感器参数Table 2 Parameters of navigation sensors
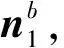
(58)
(59)
则期望的姿态角速度为:
(60)
3.2 仿真结果
假设导航制导控制周期为1 s,动力下降过程持续30 s,着陆器从初始位置到达目标点上方100 m。在式(61)所示的着陆区域内随机生成500个特征点。
D={(x,y)|x,y∈[-1500 m, 1500 m]}
(61)
利用动力下降段第一幅图像中包括着陆点在内的三个不共线特征点构建相对导航坐标系。首先分析着陆器仅利用本体系下着陆点位置矢量导航时的姿态可观测度。式(56)中矩阵Oa的条件数倒数的变化曲线如图5所示。从图中可以看出,仅利用初始时刻的观测量,可观测度矩阵不满秩,可观测度为0,说明仅利用一个时刻的观测量不能使系统可观。随着序列观测的累积,可观测度矩阵满秩,系统可观测度趋于稳定。
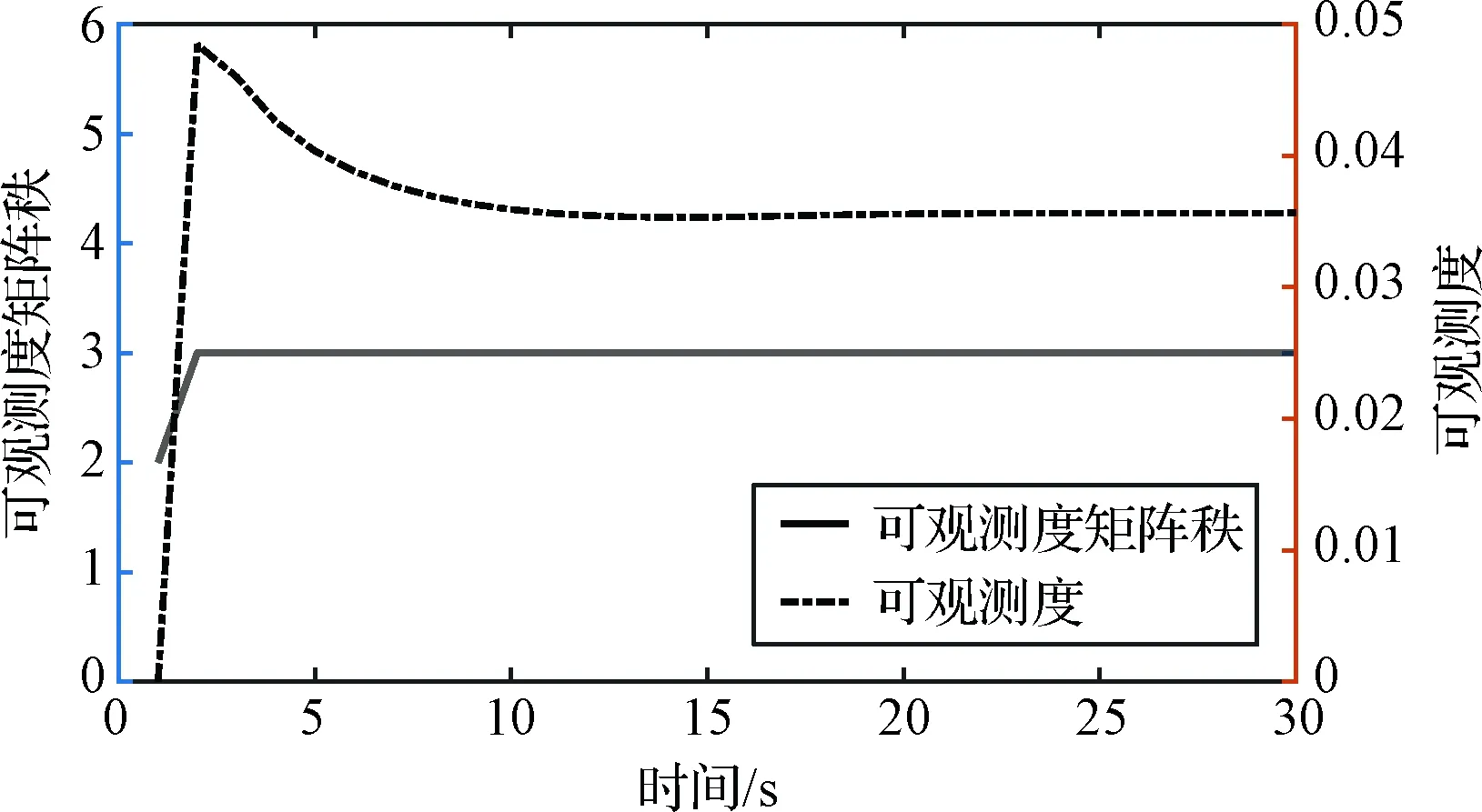
图5 姿态可观性及可观测度仿真结果Fig.5 The simulation results of lander’s observability and observability degree
根据相机参数及着陆器初始状态参数模拟观测到的特征点数量如图6所示。特征点在导航坐标系下的位置误差如图7所示。随着探测器高度降低,可用特征点数量逐渐减少。由于探测器高度降低时,同一个像素点对应的距离减小,因此在图像处理精度相同的前提下,特征点测量精度提高,且雷达测距精度也提高,因此通过测量计算得到的特征点位置误差逐渐减小。
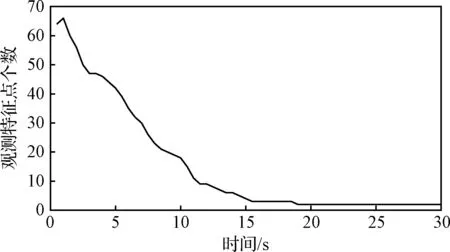
图6 可观测到的特征点数量Fig.6 The number of available feature points
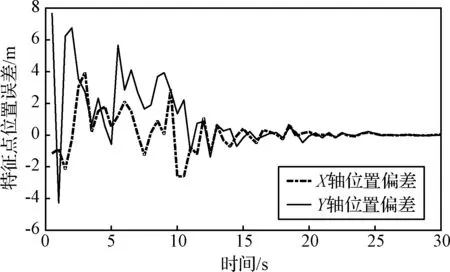
图7 特征点在导航坐标系下的位置误差Fig.7 Position errors of a feature point in relative navigation reference frame
通过蒙特卡洛仿真分析相对导航精度,并结合制导方法分析最终落点精度。500次蒙特卡洛仿真的着陆器状态误差及3σ误差界如图8所示。图中子窗口给出了动力下降段最后10 s的误差结果。从仿真结果可以看出,着陆器最终的3σ位置估计精度优于5 m,速度估计精度优于0.5 m/s,姿态估计精度优于0.5°。具体精度数据见表3。
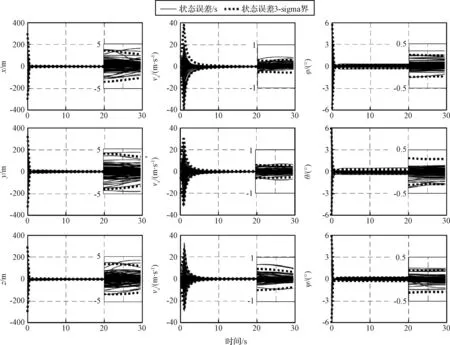
图8 蒙特卡洛仿真位置速度误差及3σ误差界Fig.8 Position, velocity and attitude errors and 3σ error bounds in Monte Carlo simulations
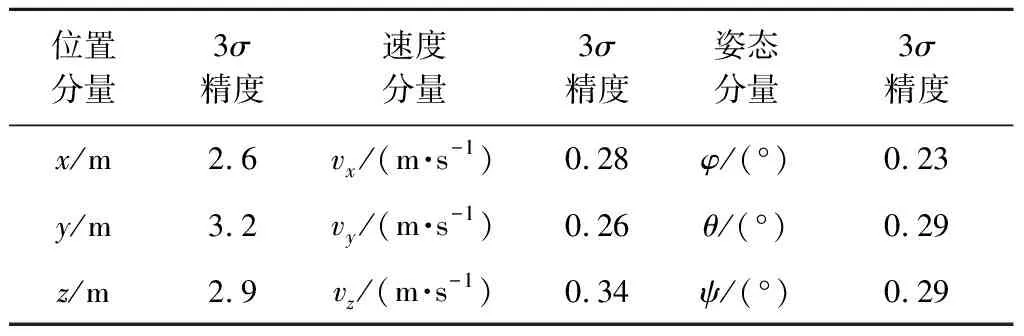
位置分量3σ精度速度分量3σ精度姿态分量3σ精度x/m2.6vx/(m·s-1)0.28φ/(°)0.23y/m3.2vy/(m·s-1)0.26θ/(°)0.29z/m2.9vz/(m·s-1)0.34ψ/(°)0.29
着陆器3σ着陆误差椭圆如图9所示。可以看出,在施加控制的作用下,着陆器可以从不同的初始状态到达目标着落点附近,实现定点软着陆,且着陆精度与导航精度近似。
4 结 论
针对行星动力下降段视觉绝对导航自然路标匮乏的问题,本文提出了利用光学导航相机与三波束雷达的相对导航方法。从导航相机观测中选取三个不共线特征点构建相对导航坐标系,结合雷达测距信息可获得特征点在相机坐标系及相对导航系下的三维位置矢量,以特征点在相机系下的位置矢量为观测量,结合着陆器姿轨动力学方程,利用扩展卡尔曼滤波,实现了着陆器相对目标点的位姿估计。
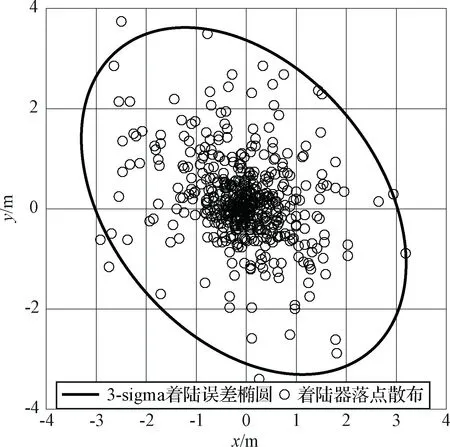
图9 3σ着陆误差椭圆Fig.9 The 3σ landing error ellipse
通过可观测度分析可知,仅利用一个特征点的观测量即可使导航系统可观。数学仿真表明,着陆器的三轴位置估计精度可优于5 m,速度估计精度可优于0.5 m/s,姿态角估计精度可优于0.3°。在相对导航的基础上,结合轨迹制导与控制,可实现火星定点软着陆。
