一种综合优势下的空空导弹接力制导混合优化方法
2019-03-14范盘龙李卿莹高晓光
李 波,范盘龙,李卿莹,高晓光
(1. 西北工业大学电子信息学院,西安 710129;2.中国电子科技集团公司数据链技术重点实验室,西安 710068; 3. 中国飞行试验研究所,西安 710089)
0 引 言
20世纪末期,信息技术日新月异,由此在军事上引发了一场巨大的变革。传统的各自为战的作战样式已不能满足数字化战争的需求。随着网络中心战[1]理念的发展,以网络为中心的作战样式已逐步演变为数字化战争的主要模式[2-3]。多机协同空战是网络中心战的一种组成部分,导弹接力制导技术是多机协同空战中的关键技术之一,是协同制导的一种具体表现形式。
作战飞机上挂载的中远程空空导弹在攻击过程中,其制导阶段需要周期性地接收来自发射载机的指令来修正弹道。但面对未来复杂的战场环境,载机发射完导弹之后可能会面临敌方的威胁和干扰等而被迫退出制导[4-5],这时就需要实施多机协同接力制导[6-7],以提升我方战机的生存能力和空空导弹的打击精度,同时提升我方整体空战效能。现有的大多公开文献[8-14],主要都是针对防空反导背景下的协同制导律的研究和设计,并没有涉及到导弹接力制导技术。文献[15]研究了固定和可切换定向通信拓扑的多导弹协同制导问题,提出了分布式协同制导律以达成相邻导弹间的信息共享,进而实现整体的协同攻击。文献[16]提出了制导优势的概念并建立了相应的数学模型,但其数学模型较为简化,未考虑协同作战飞机抗干扰的能力和制导精度的能力等因素。文献[17]利用飞机、导弹和地面设备等多种作战平台提供的数据为协同制导提供依据,引出了信息矩阵并应用最优方法量化目标的空间位置,但它所使用的制导策略仅服务于抵御来袭目标的拦截导弹,并不是接力引导导弹攻击目标。因此,研究空空导弹接力制导技术对于现代超视距空战的战法创新意义重大,在实战中具有较强的应用价值。
本文针对空空导弹接力制导的特点,充分考虑作战飞机对导弹的优势、对目标的态势优势、敌方飞
机对我方飞机的威胁度以及敌我双方飞机空战能力四方面,详细构建了综合制导[18]优势模型。而后在综合优势模型的基础上建立了中制导权移交决策模型,该模型属于典型的非线性规划模型,且为NP问题。考虑到粒子群算法具有原理简单、收敛速度快、易于求解计算量大的问题的特点,拟用粒子群算法解决该NP问题。又考虑到粒子群算法搜索能力差且精度不高的不足,本文最终采用粒子群遗传混合算法,即在粒子群算法的基础上加入遗传算法中的交叉和变异因子来求解该移交决策问题,为合理的交接决策提供理论依据。
1 作战飞机综合制导优势评估模型
作战飞机综合制导优势评估模型就是通过综合考虑编队内各战机的性能、位置、姿态等因素来评估其接力制导能力[19],是实施空空导弹接力制导的基础。
1.1 作战飞机对导弹的优势模型
1)角度优势函数
作战飞机指令天线的最大搜索角为φmax,空空导弹尾部天线的最大工作角为θmax,构造作战飞机对导弹的角度优势函数如下:
(1)
2)距离优势函数
制导飞机与导弹之间的距离越小,飞机对导弹的距离优势越大。假设飞机雷达最大制导距离为dmax,则构建距离优势函数如下:
(2)
3)制导精度优势函数
协同接力制导飞机对导弹实施中制导需要满足一定的精度要求。设δn表示导弹所需要的制导精度,δ表示飞机能够提供的制导精度。构建制导精度优势函数:
(3)
4)抗干扰能力
作战飞机的抗干扰能力越强,对导弹的制导优势越大。飞机抗干扰能力的优势函数如下:
Sgui_ε=ε
(4)
式中,ε为抗干扰因子,在[0,1]区间内取值,且ε值越大,抗干扰能力越强。
5)作战飞机对导弹总的优势
综合上述4个优势函数,构建作战飞机对导弹总的优势函数:
(5)
式中,0≤μ1,μ2≤1,μ1+μ2=1;l1,l2为加权系数,l1+l2=1。本文μ1,μ2,l1,l2均取0.5。
1.2 作战飞机对目标的态势优势模型
图1为协同作战飞机与目标的相对几何态势示意图。
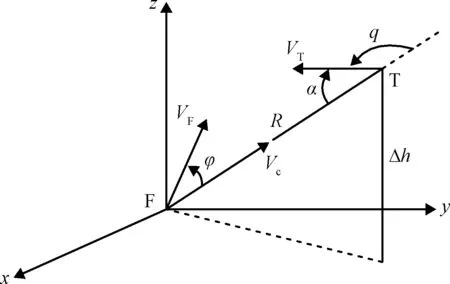
图1 作战飞机与目标机的相对几何态势示意图Fig.1 The relative geometric situation of aircraft and target
图1中:F为我方作战飞机,T为目标机,VF和VT分别为我方飞机与目标机的速度向量,R为敌我距离向量,φ为目标方位角,q为目标进入角,VC为目标接近速度向量,Δh为高度差,xyz为惯性坐标系。
1)角度优势函数
根据作战飞机与目标机的相对几何态势,目标方位角φ越大,攻击范围就会越小,优势相应变小,由此构建方位角优势函数如下:
Ssit_φ=
(6)
式中,φrmax为雷达最大搜索方位角,φmmax为导弹最大离轴发射角,φrmax为导弹最大不可逃逸区圆锥角。
另外,目标进入角q越大,导弹攻击区范围增大,优势相应增大,由此构建进入角优势函数如下:
(7)
由于目标方位角和进入角之间存在较强的耦合关系,因此构建总的角度态势优势函数如下:
Ssit_α=Ssit_φβ1·Ssit_qβ2
(8)
式中,β1,β2为权值系数,且0≤β1,β2≤1,β1+β2=1。β1随着φ的增大而减小,取值如下:
(9)
2)距离优势函数
设协同作战飞机机载雷达的最大探测距离为Drmax,空空导弹最大射程为Dmmax,导弹不可逃逸区最大距离为Dkmax,最小距离为Dkmin,a为与目标进入角有关的约束系数,构建作战飞机对目标的距离优势函数如下:
(10)
式中:
3)接近速度优势函数
在多机协同空战中,我方作战飞机对目标的接近速度优势与其对目标的角度优势和敌我距离密切关联。具体分析如下。
(1)当协同作战飞机相对目标角度占优,即Ssit_α≥0.5时,应当尽量减小敌我距离R,此时接近速度Vc应当大于零;
(2)当协同作战飞机相对目标角度不占优,即Ssit_α<0.5时,应当尽量增大敌我距离R,此时接近速度Vc应当小于零。
由此构建作战飞机对目标的接近速度优势函数如下:
(11)
式中,τc为常值,大小与接近速度优势函数曲线的变化有关。本文τc取300。
4)高度优势函数
根据高度差Δh构建高度优势函数为:
(12)
5)总的态势优势
综合考虑上述4个优势函数并结合其相互关系,构建我方作战飞机对目标总的态势优势函数为:
Ssit=m1(Ssit_αλ1·Ssit_Rλ2)+m2Ssit_vc+m3Ssit_h
(13)
式中,m1,m2,m3为加权系数,且0≤m1,m2,m3≤1,m1+m2+m3=1;λ1,λ2为权值系数,且0≤λ1,λ2≤1,λ1+λ2=1。本文λ1,λ2均取0.5;m1取0.6,m2,m3均取0.2。
1.3 敌方飞机对我方飞机的威胁度模型
敌我双方空战,敌方飞机会对我方作战飞机产生威胁,可以用敌方飞机相对于我方的优势来评估。下面结合图1分别从角度、距离、速度三个方面来评估敌方飞机对我方飞机的威胁度。
1)角度威胁函数
图1中α为目标航向角,规定α左偏为正,右偏为负,构建角度威胁函数如下:
(14)
式中,ψrmax为敌方飞机雷达最大搜索角,ψmmax为敌方导弹最大攻击角度,ψkmax为敌方导弹不可逃逸区最大角度。
2)距离威胁函数
设敌方导弹不可逃逸区最小距离为Rkmin,敌方导弹不可逃逸区最大距离为Rkmax,敌方导弹最大射程为Rmmax,敌方机载雷达最大探测距离为Rrmax,分析双方几何态势,构建距离威胁函数如下:
(15)
3)速度威胁函数
根据敌方飞机速度VT以及我方飞机速度VF构建速度威胁函数:
(16)
4)总的威胁度
综合上述三个威胁函数,考虑角度与距离之间较强的耦合性,得出敌方飞机对我方飞机总的威胁度为:
Sthr=n1(Sthr_αω1·Sthr_Rω2)+n2Sthr_v
(17)
式中,ω1,ω2为权值系数,且0≤ω1,ω2≤1,ω1+ω2=1;n1,n2为加权系数,且0≤n1,n2≤1,n1+n2=1。本文ω1,ω2均取0.5;n1取0.85,n2,取0.15。
1.4 作战飞机效能优势模型
我方作战飞机效能优势是影响其协同制导能力的关键因素之一。
假设我方作战飞机空对空作战能力指数为CF,敌方作战飞机空对空作战能力指数为CT,据此构建我方作战飞机的效能优势函数为:
(18)
1.5 作战飞机综合制导优势函数
综合作战飞机对导弹的优势、对目标的态势优势、作战效能优势以及敌方飞机对我方作战飞机的威胁,构建综合制导优势函数如下:
S=k1Sgui+k2Ssit-k3Sthr+k4Sc
(19)
式中:k1,k2,k3,k4为加权系数,且0≤k1,k2,k3,k4≤1,k1+k2+k3+k4=1。本文中k1取0.4,k2取0.3,k3取0.2,k4取0.1。
2 空空导弹中制导权移交决策问题建模
空中战场环境的复杂性使得不能只单一追求某架作战飞机对某一导弹制导优势的最大化,协同空战中常常是多架飞机同时制导多枚导弹对敌多个目标进行攻击,为了提高我方整体空战效能,需要追求我方作战飞机对所有已发射空空导弹制导优势的最大化。因此建立以下空空导弹中制导权移交决策模型。
假设我方有M架可参与接力制导的作战飞机(遇到威胁请求接力制导的飞机不可参与决策),有N枚导弹等待制导交接,根据作战飞机综合制导优势评估模型,第i架飞机相对于第j枚导弹的制导优势为Sij,且第i架飞机最多可制导Li枚导弹,用xij表示第i架飞机是否对第j枚导弹实施中制导(当xij=1时,为是;当xij=0时,为否),构建如下接力制导决策矩阵:
(20)
由此多机协同接力制导决策问题转化为寻找一组解X使得我方参与接力制导的飞机对已发射空空导弹的制导优势达到期望的最大值,即每架参与接力制导的飞机对导弹的制导优势相加和要为最大,用J(X)表示目标函数,则有:
(21)
根据飞机性能以及制导规则,需对目标函数作以下三个约束限制:
约束条件1:xij只能取0或者1,即:
xij∈{0,1}
约束条件2:每枚空空导弹最多只能由一架飞机实施接力制导,即:
约束条件3:每架飞机最多只能制导Li枚导弹,即:
针对这种NP问题,本文采用遗传粒子群混合算法对该问题进行寻优求解。
3 基于遗传粒子群混合算法的空空导弹中制导权移交策略
粒子群优化算法是一种基于群体协作的随机搜索算法,其在求解复杂系统优化问题时具有简单易行、时效性好等优点。但粒子群算法存在“早熟”问题,为了避免此问题的出现,本文采用遗传粒子群混合算法(GA-PSO)对空空导弹中制导权移交决策问题进行寻优求解,即在粒子群算法中加入遗传算法(Genetic Algorithm, GA)中的交叉算子和变异算子,为粒子群中的粒子添加一个扰动项,从而使其能够较好地跳出局部最优[10]。
3.1 粒子的表现形式
在空空导弹中制导权移交决策问题中,设可参与接力制导的作战飞机集合为I={i|i=1,2,…,M},等待制导交接的导弹构成集合J={j|j=1,2,…,N},根据待交接导弹数量令每个粒子维度为N,每一个粒子的位置可以表示为1×N的向量形式,则对粒子位置进行编码如图2所示:
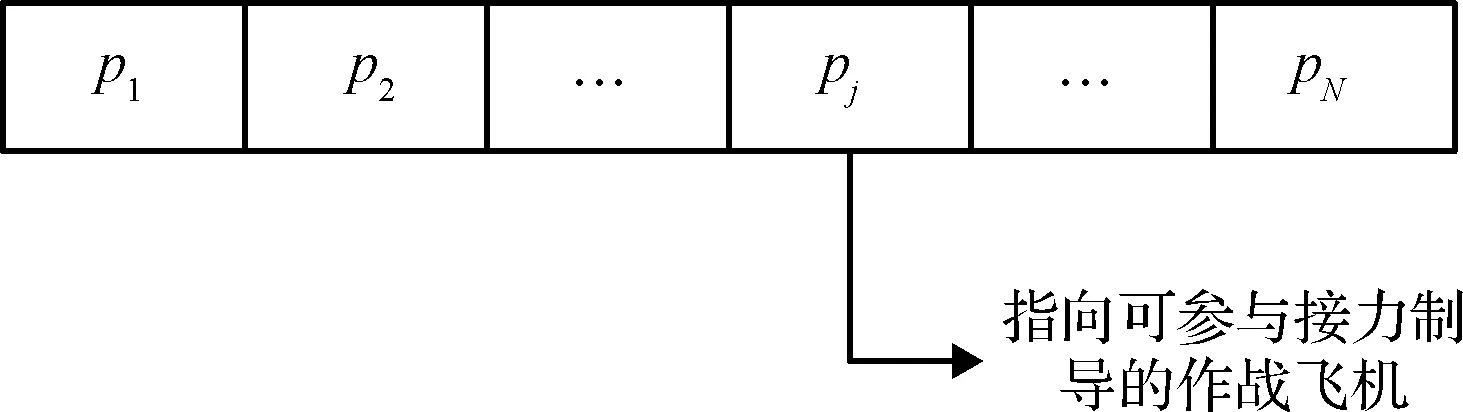
图2 粒子位置编码示意图Fig.2 Illustration of coding particle position
上图中pj指向I中第pj个元素所代表的作战飞机。据此,粒子的每一位编码均指向一架可参与接力制导的作战飞机,则粒子位置代表将N枚导弹的制导权分别交给I中相应位置的作战飞机,同时将xij置为1。然后将参数代入式(21)即可求得粒子在该位置上的目标函数值。
3.2 遗传策略
遗传算法是根据进化理论而衍生出来的一种优化算法,该算法的核心在于交叉和变异的思想。因此,本文针对粒子群算法在求解问题过程中较易陷入“早熟”的情况,运用遗传算法中的交叉算子和变异算子对群集中的粒子进行小概率扰动,以便整个群体能够跳出局部最优。
3.3 算法过程描述
图3为混合算法流程图,具体步骤如下:

图3 遗传粒子群混合算法流程图Fig.3 Flow chart of genetic particle swarm hybrid method
第1步:设置遗传粒子群混合算法的相关参数,主要包括种群规模大小、惯性因子、迭代次数、加速度因子、最大最小速度、位置范围,以及遗传算法的交叉操作概率和变异操作概率(本次实验设粒子种群数量为10,最大迭代次数为50,粒子速度在[-1,1]区间内取值,加速度因子均设为2);
第2步:初始化种群中各个粒子的位置及速度;
第3步:利用式(21)中目标函数计算粒子群中各个体的适应度值;
第4步:判断指向第i架飞机的指针在一个粒子位置中的出现次数是否超过Li,如果是,则将该粒子的目标函数值置为0;
第5步:更新粒子个体最优位置和最佳适应度以及群体最优位置和最佳适应度;
第6步:更新粒子速度,对于速度大于最大速度的粒子,将其速度置为最大速度,对于速度小于最小速度的粒子,将其速度置为最小速度;
第7步:更新种群中所有的粒子位置,对于粒子位置中大于最大位置的元素,将其置为最大位置,对于粒子位置中小于最小位置的元素,将其置为最小位置;
第8步:对粒子群个体实施个体最优交叉操作、群体最优交叉操作,并判断交叉后代是否有效,即判断其中各架飞机编号的出现次数是否超过其最大可同时制导的导弹数目,若无效则替换交叉编码的相应位,继续进行交叉操作,若有效且新个体适应度值大于旧个体则更新粒子位置,进行下一步操作;
第9步:对粒子个体实施变异操作,并判断变异后代是否有效,若无效则改变变异编码位置,继续进行变异操作,若有效且新个体适应度值大于旧个体则更新粒子位置;
第10步:判断是否到达最大迭代次数,如果是,则终止,否则跳至第三步循环执行。
4 仿真分析
作战想定:我方有C1,C2,C3,C4,C5,C6,C7,C8共8架作战飞机,在水平面内的初始位置分别为(110,130),(110,122),(110,115),(110,110),(115,110),(121,110),(129,110),(136,110),单位:km;初始高度均为7 km;初始速度均为380 m/s;我方每架战机最多可同时制导2枚空空导弹。敌方有T1,T2,T3,T4共4架作战飞机,其水平初始位置分别为(10,20),(15,15),(20,10),(25,5),单位:km;初始高度均为5 km;初始速度320 m/s。导弹速度为1000 m/s。我方作战飞机性能参数如表1所示。我方导弹性能参数如表2所示。敌方作战飞机与导弹性能参数如表3所示。
本次仿真实验分别采用粒子群算法、遗传粒子群算法和动态规划对导弹制导权移交决策问题进行求解。
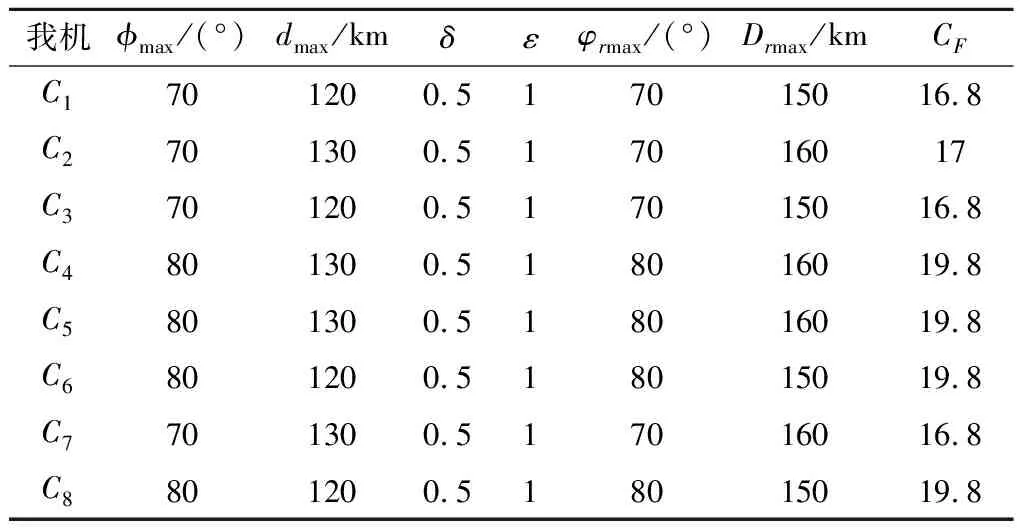
表1 我方战机性能参数Table 1 Performance parameters of aircrafts
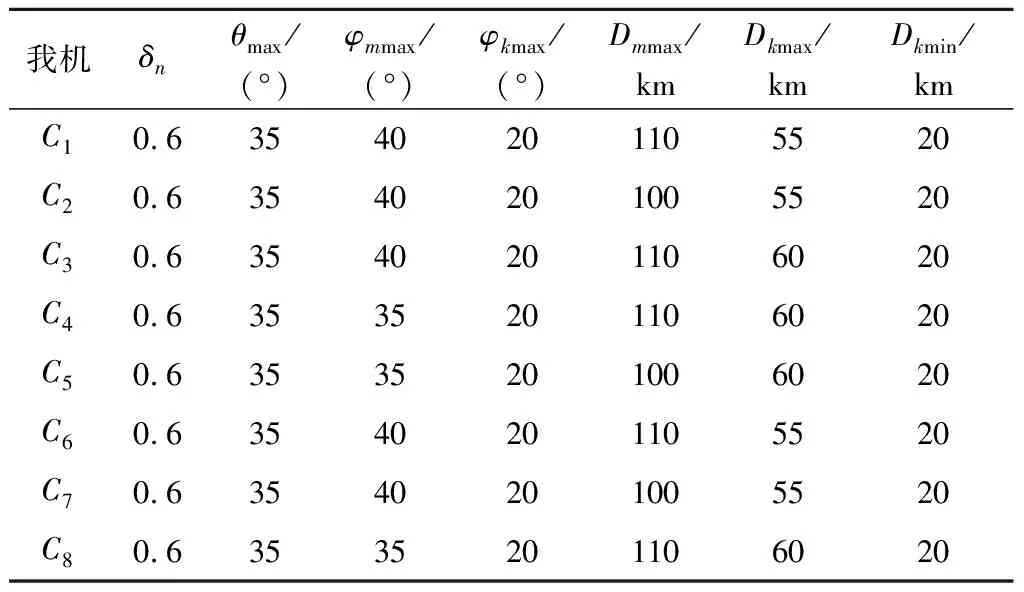
表2 我方各机导弹性能参数Table 2 Performance parameters of missiles
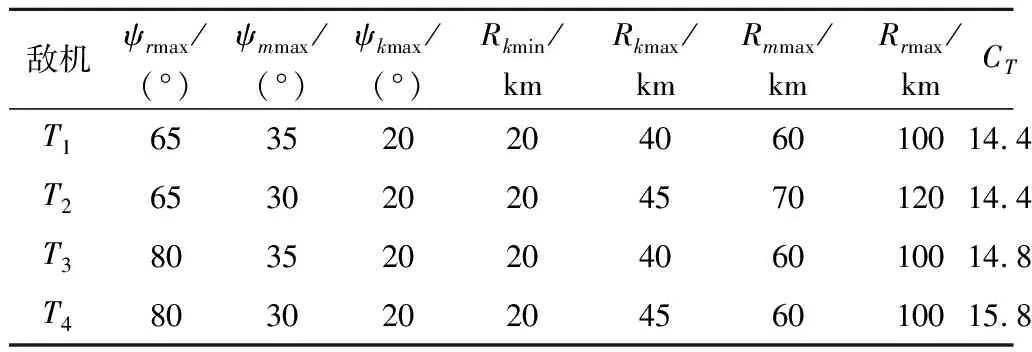
表3 敌方战机及导弹性能参数Table 3 Performance parameters of enemy aircrafts and missiles
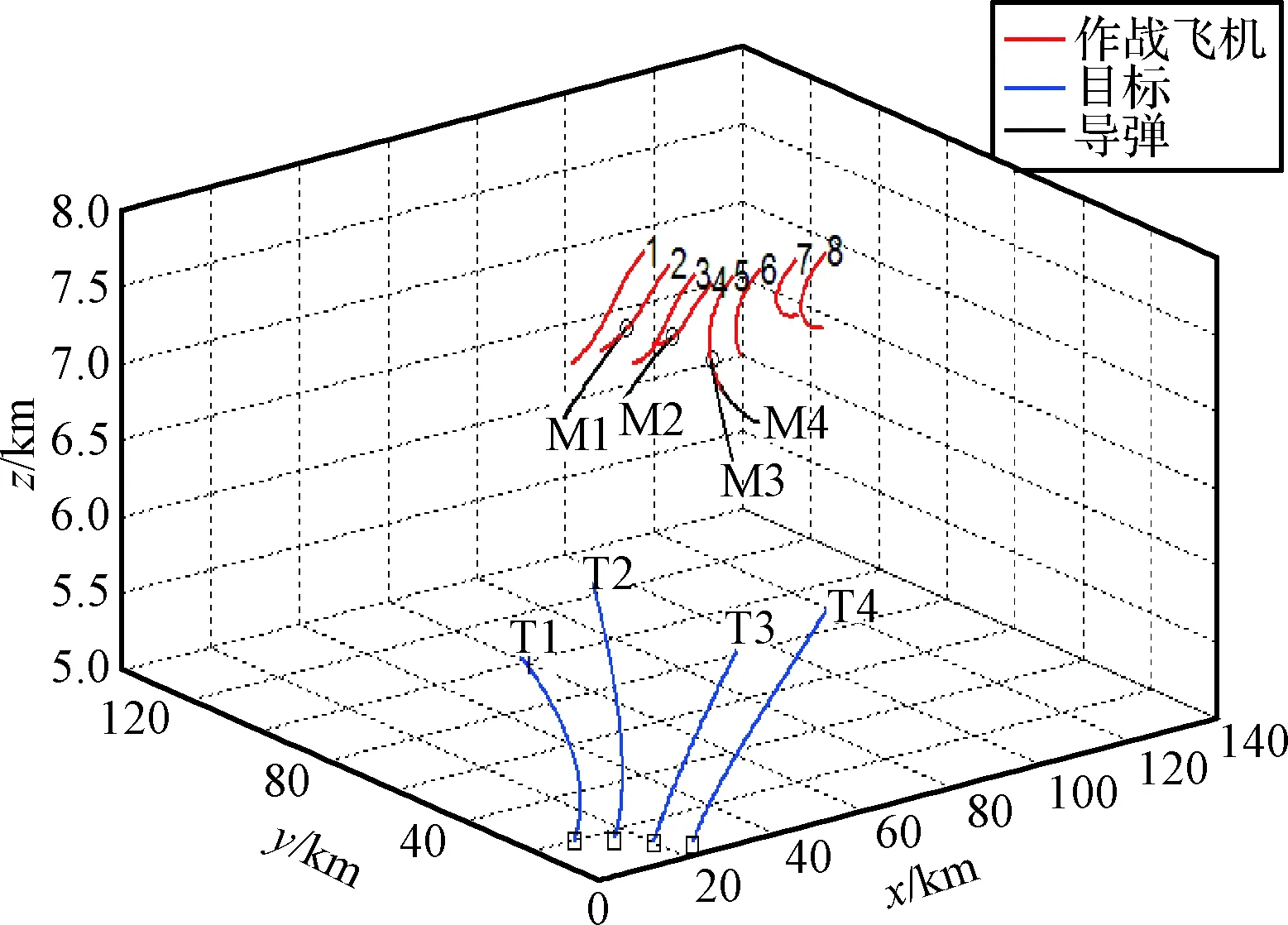
图4 多机空战轨迹图Fig.4 Trajectory of multi-aircraft in air combat
仿真攻击方案为:C2发射导弹M1攻击T1;C4发射导弹M2攻击T2;C5发射导弹M3,M4分别攻击T3,T4;导弹制导方式均采用比例导引。我方飞机、空空导弹以及敌方飞机飞行轨迹示意图如图4。
在导弹攻击过程中,我方作战飞机C4,C5受到敌方T3飞机的威胁在第114秒请求接力制导。根据作战飞机综合制导优势函数计算出我方8架战机对4枚已发射导弹的制导优势值如表4所示:
采用普通粒子群算法得到的空空导弹中制导权移交策略为:导弹M2由飞机C4向C3交接;导弹M3由飞机C5向C7交接;导弹M4由飞机C5向C6交接。
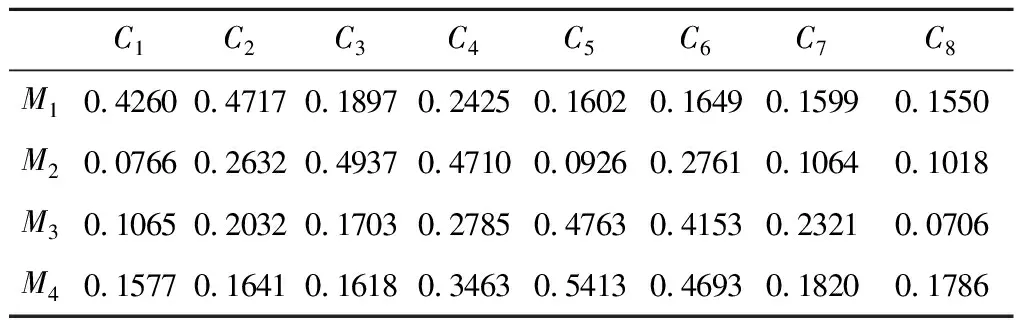
表4 作战飞机综合制导优势值Table 4 Integrated guidance superiority of combat aircraft
采用遗传粒子群混合算法得到的空空导弹中制导权移交策略为:导弹M2由飞机C4向C3交接;导弹M3由飞机C5向C6交接;导弹M4由飞机C5向C6交接。
采用动态规划方法得到移交策略与采用遗传粒子群混合算法得到结果相同。
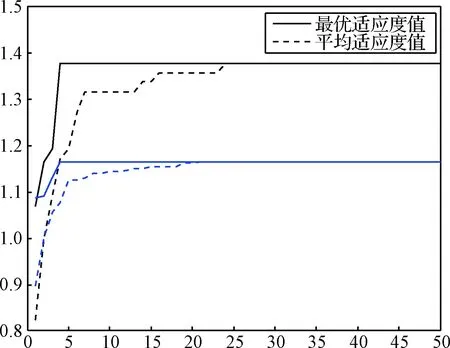
图5 适应度值曲线Fig.5 The graph of fitness value
遗传粒子群混合算法和普通粒子群算法解算空空导弹制导权移交决策问题过程中最优适应度值与平均适应度值随迭代次数的变化曲线如图5所示,
其中适应度值就是式(21)中的目标函数值,上方的实线和虚线表示混合算法的结果曲线,下方的实线和虚线表示普通粒子群算法的结果曲线。采用动态规划方法得出的适应度值与迭代次数无关,为固定值,其值与遗传粒子群混合算法得到的最终最优适应度值相同。
我方8架作战飞机对M1,M2,M3,M4四枚导弹的综合制导优势值随时间的变化曲线如图6所示。图中,横坐标表示时间,纵坐标表示制导优势值。四个子图从左到右从上到下依次表示飞机对导弹M1,M2,M3,M4的制导优势曲线。
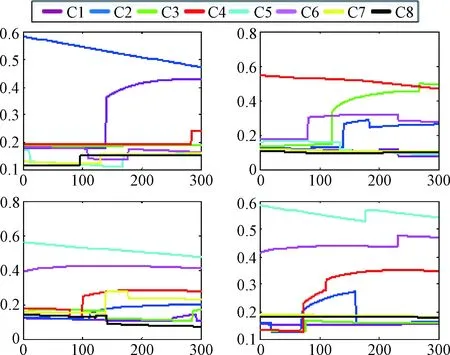
图6 制导优势曲线Fig.6 The graph of guidance superiority
由图6制导优势曲线可以看出,在本次作战想定设置条件下,本文所提出的遗传粒子群混合算法求得的制导权移交策略解是当前阶段的最优解,它解决了普通粒子群算法过早陷入早熟而得到次优解的问题,使得待交接导弹在制导权的移交过程中能够匹配到最合适的作战飞机,从而提高了我方机群的整体作战优势,增大了导弹命中敌方空中目标的概率。
在仿真过程中,将粒子群优化算法与遗传粒子群混合算法以及动态规划方法进行了对比,三种算法求解时间及所得最佳适应度值如表5所示:
从表5可以看出:采用遗传粒子群混合算法得到的最佳适应度值要比普通粒子群算法得到的最佳值要高出15.3%,而且在与动态规划方法得到相同

表5 三种算法求解时间和最优适应度值Table 5 Solving time and optimal fitness values of three algorithms
最优适应度值的前提下,其耗时要比动态规划方法少46.9%;此外,由图5可知:除了最佳适应度值外,遗传粒子群混合算法在整个迭代过程得到的适应度值都要普遍优于普通粒子群算法。所以综合来说,遗传粒子群混合算法不仅合理有效,而且采用该算法所得出的解还要比传统的粒子群算法得出的解更合适,所耗费的时间要比动态规划这样的非线性规划方法更少。
5 结 论
结合多机协同接力制导的情境及特点,建立了作战飞机综合制导优势评估模型,该模型为接力制导决策提供了依据,减小了制导交接对导弹打击精度的影响,保证了我方作战效能。另外,建立了空空导弹中制导权移交决策问题模型,并使用遗传粒子群混合算法求解,有效避免普通粒子群优化算法的“早熟”现象,降低了粒子群随机搜索难以跳出局部最优的概率,提高了求解精度,在解决大规模空战制导交接决策问题时具有良好的时效性。
