柔性特征的太阳电池翼在轨载荷分析

2019-03-14刘汉武胡震宇

宇航学报 2019年2期

张华，刘汉武，胡震宇，张武

(1. 上海宇航系统工程研究所，上海 201109；2. 上海市空间飞行器机构重点实验室，上海 201108)

0 引言

太阳电池翼(以下简称太阳翼)为满足运载器的包络尺寸限制，发射段一般处于收拢状态并通过火工机械装置压紧在航天器的舱体上，航天器入轨后再将太阳翼展开并保持其稳定的运行状态。为满足航天器上大量有效载荷的能源需求，一般要求太阳翼展开后其尺寸尽可能大，同时由于发射段对航天器重量的限制，还要求太阳翼的质量需尽可能的轻。此外，根据探测任务需求，航天器在轨可能实施一系列的在轨动作，如轨控(主发动机开机，轨道机动)、舱段或器间(主、被动目标)分离、交会对接(追踪飞行器、目标飞行器)等在轨动作，处于展开状态的太阳翼在上述过程中需具备较强的承载能力，以确保太阳翼不会出现永久性的物理变形或损伤。在上述多个约束条件下，太阳翼展开后具有尺寸大、质量轻、刚度高、承载强等特点，为确保在轨安全运行，通过仿真计算、试验验证等手段分析在轨载荷作用机理，对太阳翼的设计具有重要意义。

针对太阳翼在轨若干动力学问题，国内学者开展了较多研究。2006年王巍等[1]介绍了航天器柔性附件如太阳翼铰接结构中的非线性动力学现象和对该类问题的研究思路，并对其研究发展前景进行了总结。2008年刘望[2]采用两种不同的模型对太阳翼进行了动力学分析，提出了基于静平衡位置变化的弹性振动描述方法，较好地反应了太阳翼在轨飞行中的动力学变形。2013年Li等[3-4]研究了太阳翼在轨运行面临的空间热环境引起的热振动问题。2014年赵志萍等[5]对大面积电池翼的发展和趋势进行了研究和综述；2015年罗文[6]采用混合坐标法对太阳翼卫星进行柔性多体系统建模，描述了卫星大范围运动和太阳翼刚柔耦合运动形式，对不同铰链等效刚度的太阳翼固有频率、振型进行了计算,2015年Shi等[7]和Zhu等[8]主要研究了机构运动与太阳翼振动的相互影响。2016年Zhang等[9]通过三维、非接触、自动、高精度的测试系统对太阳翼的变形开展了测试工作，测试结果具有很高的稳定性，耿盛韦等[10]研究了预应力对太阳翼动力学特性的影响，发现只有柔性阵面上的张紧力影响最为显著。上述研究主要集中于太阳翼的建模、动力学特性分析等方面，关于在轨载荷设计和分析方面较为少见，但该项内容又是太阳翼主承载结构及其相关机构在设计过程中最重要的输入条件，尤其是我国探月工程中电池翼的设计还需要考虑更为复杂工况下(如近月制动、环月对接、多次分离以及离月加速等)的承载能力，需对其开展各个在轨工况下的载荷分析以作为强度、结构设计的依据。本文从工程应用角度出发，介绍了一种基于柔性多体理论的太阳翼在轨载荷分析方法，给出了在轨典型工况下太阳翼主要部件或节点的载荷，并结合地面试验结果，验证了计算方法的有效性和合理性，为工程关键技术攻关和实践应用奠定了坚实基础。

1 太阳翼动力学模型

1.1 太阳翼动力学模型建立

太阳翼主要由基板、板间铰链机构、根部铰链机构、电池电路等部分组成(见图1)。太阳翼动力学建模中，将基板简化为板单元，电池电路以非结构质量均布于基板；根部及板间铰链机构力学参数主要通过静刚度试验数据进行等效，以弹簧元形式连接各个基板，搭建太阳翼整体有限元模型。此外，还需开展整个太阳翼的地面模态试验，考虑空气阻尼(动力学模型以流固耦合形式反映)、地面悬挂系统(绳索张紧力、摩擦等因素)对太阳翼动力学特性的影响(见图2)，由此修正太阳翼模型参数。撤去地面环境和吊挂装置影响后，即可获得接近在轨零重力状态下的具备真实动力学特性的有限元模型(见图3)。图4为太阳翼在轨状态根部铰链固支边界下的前六阶模态分析结果，表1为计算与试验的对比值，误差在5%左右。经过模型修正后，本文的分析研究均以在轨状态的动力学模型为基础。

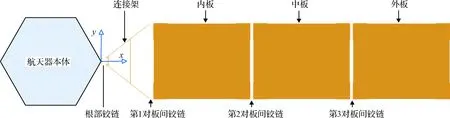
图1 太阳翼坐标系及名称标识Fig.1 The coordinate and flag of solar cell

1.2 太阳翼动力学模型缩聚

由于有限元模型在节点自由度数目方面一般都较为庞大，在基于混合坐标法处理中心刚体-太阳翼刚柔耦合动力学模型时，在保证计算精度前提下往往又要求求解的微分方程数目不宜过大，此时一般会将规模较大的有限元模型利用有限自由度来近似表示。将太阳翼划分成多个子结构并通过界面自由度相连，每个子结构的位移便可通过内部位移ui和界面位移ub表述。子结构的振动方程按照内部物理自由度和界面物理自由度可写为：

(1)

式中：fb为界面力。对于固定界面式(1)中界面物理自由度ub为零，可求解得到其正则化模态或固定界面固有模态φit=[φ1,φ2,…]。通过子结构平衡方程可变换为：

(2)

φib为约束模态，由式(3)将子结构物理自由度

图2 带地面试验系统的太阳翼动力学模型Fig.2 Solar cell dynamic model with ground test system

图3 在轨零重力状态下的有限元模型Fig.3 Solar cell dynamic model based on space zero gravity

图4 在轨零重力状态下太阳翼前6阶模态振型Fig.4 Solar cell former six modes based on space zero gravity

阶数地面试验状态(试验值)/Hz地面试验状态(计算值)/Hz在轨状态(计算值)/Hz备注第1阶0.35170.364760.3676一阶外弯第2阶1.15481.06391.1986一阶内弯第3阶1.94742.01292.1978一阶扭转第4阶2.21972.35352.2134二阶外弯第5阶4.92455.23835.9959三阶外弯第6阶5.77906.01707.0470二阶扭转

变换到模态自由度q：

(3)

式中：qt为固定界面固有模态下的模态坐标，qb为约束模态下的模态坐标。将式(3)代入式(1)，并考虑子结构边界位移协调条件，通过模态变换可得到模态坐标下的广义刚度阵和广义质量阵：

(4)

(5)

本文在对太阳翼进行模态缩聚时，模态截断为前30阶，此时模态有效质量百分比已到达95%以上，且低阶的频率(如前六阶)已经很大程度反映了太阳翼的主要振型。

2 刚体-柔性体耦合动力学模型

太阳翼一般通过驱动机构、根部铰链装配在航天器上(见图1)，建立太阳翼在轨动力学模型时需考虑航天器本体的运动特性，此时通常将航天器简化为中心刚体，太阳翼表征为柔性部件。刚体按多刚体动力学理论建立方程，而柔性体采用上述缩聚后的模型，将两者组集可得到刚-柔耦合的系统动力学方程。

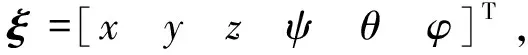
(6)

柔性体系统采用惯性坐标系和动坐标系相结合来描述其运动状态，太阳翼上任意点p位置向量表示为：

r=r0+A(sp+up)

(7)

式中：up由式(3)表示，r0为动坐标系原点在惯性坐标系中的位置向量，A方向余弦转换矩阵，sp为太阳翼未变形时任意p点在动坐标系中的位置向量。根据拉格朗日方程可以得到柔性体系统的运动微分方程如下所示:

(8)

3 在轨载荷分析

3.1 在轨分离工况

为了尽可能完成多项探测任务，航天器一般由多个舱段或多个独立飞行器连接组成，可进行多次在轨分离[11]，使之能独立完成各自的飞行任务。分离方式一般为反推发动机或弹簧推杆，目前主要以弹簧推杆为主，其优点是简单、可靠，本文以此为分离动力源，四根弹簧推杆正交布局于安装分离面上(航天器坐标系)，见图5。

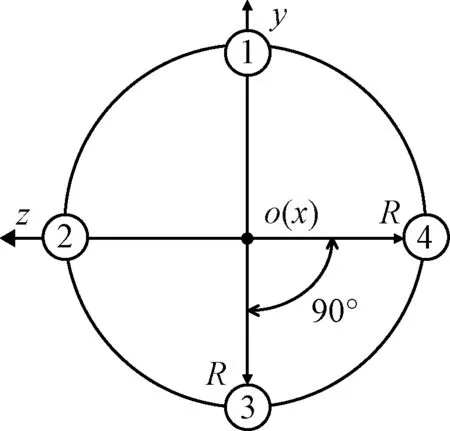
图5 弹簧推杆布局图Fig.5 The overview of spring pole

弹簧推杆数学模型可表达为如下所示：

(9)

其中，Fi是第i根杆作用的推力，uxi(≤0)是第i根杆的端面在x方向(分离方向)的位移，F0,k为推杆的初始压紧力及弹簧常数，s0是弹簧推杆的最大伸出量。当分离界面的火工装置起爆完成后，主、被动飞行器即在弹簧推力作用下以极短的时间(一般为毫秒级)沿着x(航天器本体坐标系)向分离，对太阳翼根部铰链或驱动机构而言，相对于承受了某种程度的冲击载荷，载荷的最大值一般出现在初始时刻，然后衰减。

依据飞行时序下太阳翼在轨状态，本文主要列举了主、被动飞行器分离工况下考虑电池翼与飞行器舱体水平归零(0°)、45°及垂直(90°)等三个状态(见图6)，根部铰链副弯矩计算结果分别如图7所示。

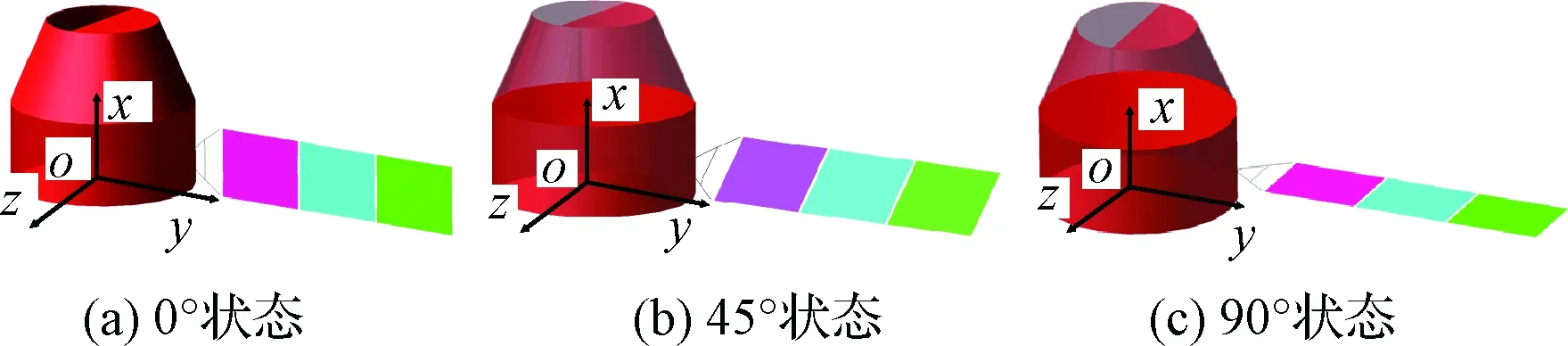
图6 太阳翼相对航天器本体坐标系的转角状态Fig.6 The rotation angular relative to spacecraft coordinate

太阳翼转角状态弯矩载荷(Nm)太阳翼坐标系MxMyMz刚性柔性刚性柔性刚性柔性0°0000151152.345°03.6106.744.3106.7131.190°00.008153.261.500.28

太阳翼在受到外部激励干扰后，由于自身弹性特征使得载荷出现了较大程度的震荡(见图7)，这与实际状态是相符的；相反，若按照传统计算方法假设太阳翼为刚体状态，太阳翼根部载荷与其转角状态已无关联，无论太阳翼处于何种转角状态，其根部x,y向弯矩均几乎为零，只有z向具有相应弯矩载荷且只与太阳翼自身质量特性和加速度有关，这与实际物理状态是不符的，由此可见太阳翼柔性特征不可忽视，此时不能再按照传统的刚体假设进行分离仿真计算，否则分析结果值将与真实情况相差较大，将给太阳翼的载荷设计带来颠覆性影响，鉴此本文后续均基于太阳翼柔性特征开展相应载荷分析。

依据上述计算结果，太阳翼0°状态的载荷最大，其次是45°转角状态，最小是90°垂直状态。在外激励作用下太阳翼三种转角状态的载荷体现了太阳翼约束模态的参与程度，90°垂直状态主要体现太阳翼外弯模态，45°状态体现了外弯、内弯及扭转模态，0°状态主要体现内弯模态。由此可见，考虑柔性特征情况下的太阳翼转角状态对其根部载荷影响较为显著，太阳翼在轨动力学特性也直接影响载荷结果的有效性。

3.2 变轨机动工况

航天器主发动机根据轨道设计时序，需在月地转移轨道实施近月制动(航天器飞抵月球)及离月加速(航天器返回时月地转移轨道)。出于保密要求，本文将主发动机长时开启产生的推力曲线及航天器质量等效为航天器本体与太阳翼组合体的质心稳态加速度载荷(见表3)，该载荷同时也会导致太阳翼产生振动，最终会使得航天器本体与太阳翼产生耦合作用。此外太阳翼的转角状态对航天器本体与太阳翼耦合作用产生的在轨载荷也有极大影响，限于篇幅，本文只列出了太阳翼处于0°水平归零和90°垂直两种状态下对太阳翼影响最大的根部弯矩载荷计算结果(见表4)，根部弯矩载荷也是开展地面静力试验验证的主要依据。

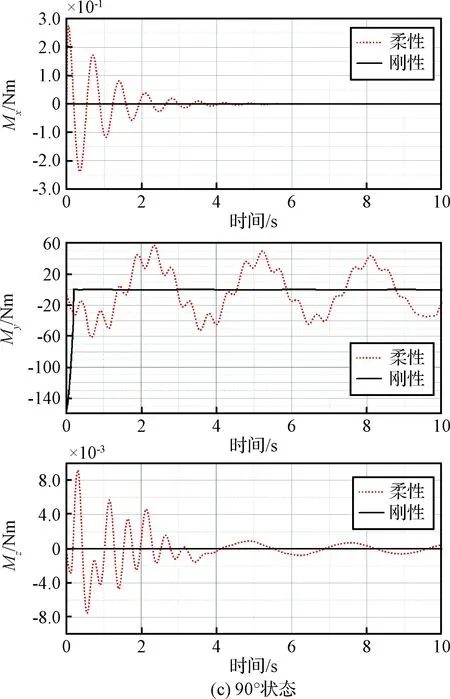
图7 分离工况下太阳翼根部弯矩载荷曲线Fig.7 The torque curve of solar cell root joint

表3 变轨机动工况组合体质心加速度载荷Table 3 The acceleration of mass center

表4 变轨机动工况下太阳翼根部载荷Table 4 Solar cell root joint torque vs orbit-transferring case

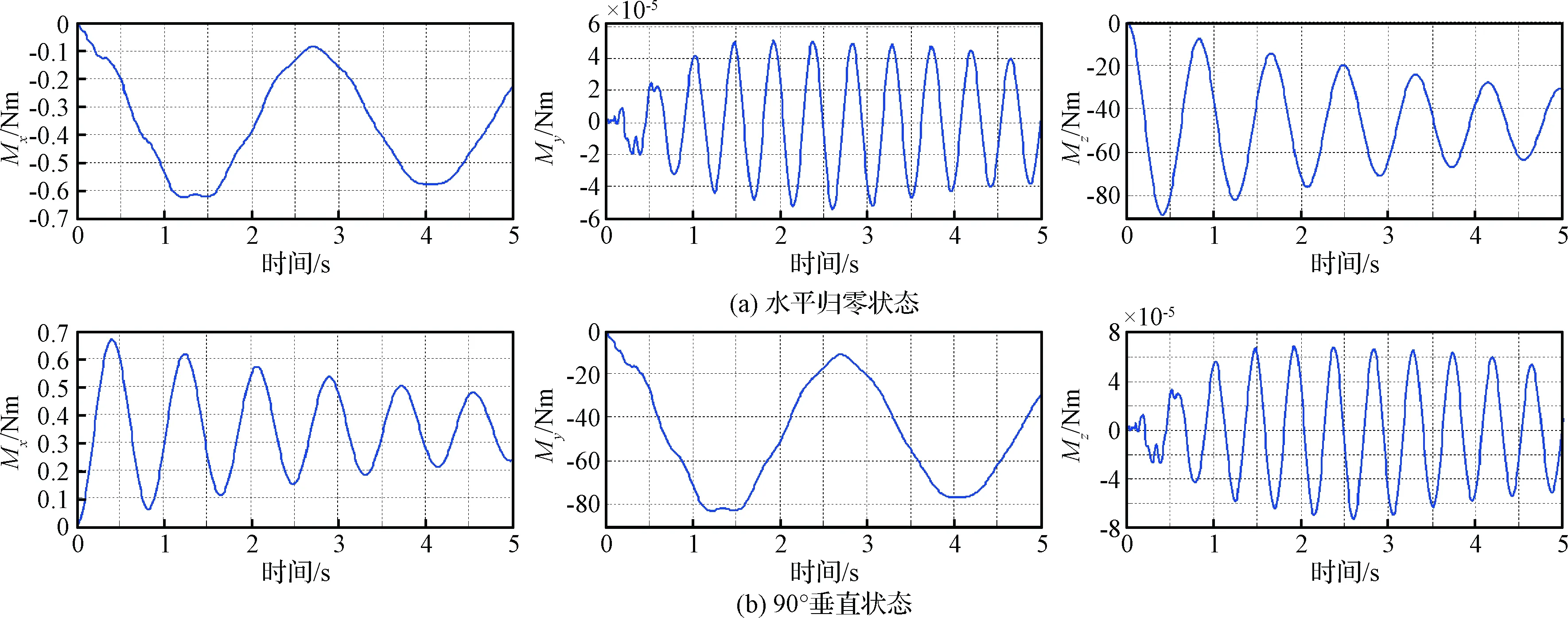
图8 近月制动工况下太阳翼根部弯矩载荷曲线Fig.8 The torque curve of solar cell root joint

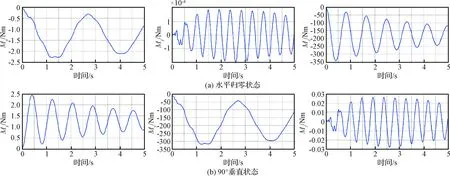
图9 离月加速工况下太阳翼根部弯矩载荷曲线Fig.9 The torque curve of solar cell root joint

根据表4计算结果，离月加速时太阳翼根部弯矩载荷是近月制动时的4倍左右。太阳翼转角在水平归零与90°垂直两种状态下的弯矩载荷相差不大，但由于太阳翼驱动机构承载能力的方向性问题，其90°垂直状态下的承载能力远小于水平归零状态。因此，在变轨机动工况下，太阳翼相对航天器的转角应尽可能水平归零，以增强抗外载荷能力。

3.3 捕获对接工况

主、被动飞行器捕获对接(x向为捕获对接方向(见图10))工况涉及两飞行器不同的姿态情况，按照捕获对接的初始条件(主、被动飞行器相对位移、速度及姿态角等)可分为单项极限偏差、极限偏差组合、随机打靶等多种状态。本文依据上述三种主要状态，筛选了17种初始条件捕获对接过程，且太阳翼转角分别在水平归零、45°状态、90°垂直等共51种仿真分析情况。

图10 主、被动飞行器捕获对接示意图Fig.10 Docking of the active and passive aerocraft

序号太阳翼转角状态太阳翼坐标系Mx/NmMy/NmMz/Nm0°0.624.366.5145°0.435.1178.390°0.42733.20°135.167245°04.8118.490°0.428.6144.80°0.574.1126.4345°0.529.4238.790°0.631.50.30°0.614.6126.6445°0.512.9219.390°022.300°0.216.949.1545°0.253.8185.290°0.227.118.40°0.445.523.7645°0.454.8159.390°0.410.572.60°0.216.953.3745°0.253.8185.290°0.227.1192.50°0.421.549845°0.444.6179.590°0.531.60.60°0.221.553.3945°0.253.5181.590°0.228.725.6

表5续

序号太阳翼转角状态太阳翼坐标系Mx/NmMy/NmMz/Nm0°0.412.253.31045°013.351.290°0.631.60.70°0.26.948.61145°0.246.1180.290°0.226.918.40°0.314.662.51245°0.411.675.890°0.623.946.90°0.29.552.91345°0.247.5181.390°0.226.925.60°0.765.4581445°047.3181.790°0.428.6192.70°0.465.157.91545°0.644.8184.890°027.11500°00581645°0.546.3185.590°033.285.40°0.641.334.21745°0.515.769.390°0.53.253

由表5可知，当太阳翼处于45°状态时，其根部载荷普遍较大，这主要与捕获对接时刻主被动飞行器的姿态和太阳翼的模态振型相关。事实上当太阳翼根部载荷越大，航天器受到太阳翼的反作用力矩也就越大，因此为了降低太阳翼与航天器的耦合影响，减轻航天器姿态控制难度，应尽可能减小捕获对接过程中太阳翼的根部载荷，使太阳翼处于水平归零或90°垂直状态，同时考虑到在轨太阳翼的阻尼特性对控制系统的贡献，太阳翼90°垂直状态有利于主、被动飞行器高精度捕获对接。

4 试验验证

通过对太阳翼上述典型在轨工况的载荷分析，太阳翼在轨飞行期间需承受较大载荷，为验证太阳翼结构是否具备承载上述各工况下载荷的能力，对太阳翼进行了多工况(0°，90°状态，其它转角状态均可分解为这两种状态)静力试验。试验加载载荷选取了上述三种工况中的最大载荷，试验过程及加载原理见图11、图12。加载过程按层级加载，每一级为5%设计载荷(上述工况计算分析得到的载荷为使用载荷，设计载荷等于使用载荷乘以1.5倍安全系数)，最终加载至设计载荷的1.1倍，连接架与根部铰链连接处局部测点应变曲线见图13，应变基本呈线性变化，表明各测点位置的结构材料仍处于线弹性范围内，未出现屈服或破坏，太阳翼结构可以承载上述各工况下的最大载荷。