多重分形模型及其在金融风险管理中的应用述评

邢春娜

(厦门大学 经济学院，福建 厦门361005)

一、引言

分形理论的基本思想最早可以追溯到17世纪数学中的递归方法，Mandelbrots首先提出分形(Fractal)一词，并开创了分形几何学。自相似性是分形的主要特征，Mandelbrot 在1963年发现棉花价格分布具有强自相似性，后来的研究表明金融时间序列普遍具有分形特征，数据分布形式不随时间标度(日、周、月等)变化，他因此认为金融的核心是分形。在分形理论基础上，Peters提出分形市场假说[1]44-50，该假说强调市场流动性、市场信息和投资期限对投资者行为的影响，很好地解释了有效市场假说无法说明的市场现象，是对有效市场假说的修正与拓展。

随着经济物理学(Econophysics)的发展，分形在经济、金融领域得到越来越广泛的应用。当前，金融时间序列具有多重分形特征已成为普遍认可的事实，来自股票、汇率和期货市场的实证分析结果都表明，金融资产收益分布除了尖峰厚尾、波动率集聚、长记忆性等特点，价格改变还随时间标度呈现不规则变化，即具有多重分形特征，多重分形模型能够比GARCH族模型更好地拟合金融数据。近几年，多重分形模型逐渐被应用于金融风险管理。鉴于国内的风险研究仍主要建立在GARCH族模型基础上，多重分形性质和模型没有得到应有的重视，本文回顾了三种多重分形模型，介绍了其研究优势以及在金融风险管理中的最新应用情况。以期能为金融风险管理者和相关领域的研究人员提供有益参考。

二、分形基本理论与多重分形模型

(一)分形

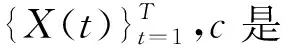
E(|X(t)|q)～c(q)tτ(q)+1

(1)

则X(t)是多重分形，q是整数，τ(·)称为标度指数，τ(0)=-1。多重分形能够反映随机过程中不同强度的波动，波动的权重随q的增大而增大。多重分形的分析方法主要有四种，分别是矩方法、柱形图方法、多重分形去趋势波动分析(MFDFA)和小波变换模极大值(WTMM)方法[2]。

(二)多重分形模型

目前应用较广泛的多重分形模型主要有：资产收益多重分形模型、马尔科夫转换多重分形模型和多重分形随机游走模型。

1.资产收益多重分形模型

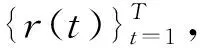
2.马尔科夫转换多重分形模型

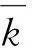
(2)

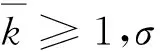
(3)

aij=Pr(Mt+1=sj|Mt=si)

(4)

其中，1是示性函数；s1，s2，…，sd是不可观测的状态；γk∈(0,1)；b∈[1,)，通常取为2，用来反映不同波动分量状态转移概率之间的联系；分量的波动周期为越大，波动周期越长。当时，式(3)对应于常见的两状态马尔科夫区域转换过程，而式(4)的这种多分量乘法结构能够实现波动率在多个状态之间的转换，并且有助于区分金融时间序列不同周期的波动。

3.多重分形随机游走模型

Bacry等将随机方差引入高斯过程构建了多重分形随机游走(MRW)模型[5]。假设X(t)是具有平稳增量的随机过程，将X(t)定义为平稳过程ωl(t)的弱极限：

(5)

其中dB(u)是均值为零、方差为σ2的白噪声过程。ωl(t)的均值和自协方差函数分别为：

E[ωl(t)]=-λ2(ln(T/l))+1)

(6)

(7)

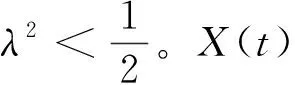
(8)

MRW模型包括三个参数，分别是描述相关性强度的间歇系数λ2，对数去相关标度ln(T)和对数标准误ln(σ)，它们捕捉了资产收益与抽样时间间隔的关系。

三、多重分形模型在风险管理中的应用

风险管理是金融工作的核心，多重分形模型为金融市场风险的度量和预测提供了新工具。目前多重分形模型主要用于市场风险在险值(VaR)指标的模拟、估计和预测。

由于资产收益波动本身就是风险的一种表现，因此与其他两个模型相比，MSM模型在风险研究方面的应用较多。Calvet和Fisher利用模拟的MSM模型估算美元兑澳元汇率的在险值[6]；Lux等对WTI原油价格日数据的分析发现，MSM模型在VaR预测方面优于GARCH模型[7]。为捕捉资产收益之间的相关性，Malo、Mawuli和Mark分别将Copula函数与MSM模型结合，前者在拟合电价现货和期货数据的基础上估计了投资组合的条件在险值(CVaR)，后者提出一种投资组合市场风险预测方法，通过与Copula-GARCH、CCC-GARCH、RiskMetrics等方法的对比分析，认为Copula-MSM能更准确地预测VaR，且结果更加稳健[8-9]。为刻画资产收益尾部特征，特别是肥尾的时变性，Herrera等在MSM模型中引入POT(Peaks-Over-Threshold)方法，利用6种商品期货价格日数据的实证分析结果显示，MSM-POT模型能够比GARCH-EVT方法更准确地预测VaR[10]。

基于资产价格和收益率多重分形特征的MMAR模型主要被应用于VaR预测。Batten等使用调整的MMAR模型和5分钟高频数据预测欧元兑美元汇率市场风险，1%VaR向前12小时和一天的样本外预测准确率高于历史模拟VaR和GARCH(1,1)模型基础上的VaR[11]；Lee等在MMAR模型基础上建立一种参数VaR，利用韩国、美国股票市场指数和美元兑韩元汇率日数据的实证结果表明，这种VaR比历史模拟VaR、正态分布和t分布假定下的VaR、GARCH模型基础上定义的VaR更准确地预测了金融市场风险[12]。

与MMAR和MSM模型相比，MRW模型目前在风险管理中的应用较少。Bacry等比较了MRW与GARCH(1，1)模型预测汇率市场风险的能力，利用加元、日元、瑞士法郎和英镑四种汇率日数据的分析结果表明，MRW模型对0.5%～10%VaR的预测效果都好于GARCH(1，1)模型[13]；Bacry等认为对数正态MRW模型在预测股指和汇率风险方面优于GARCH和tGARCH模型[14]。

金融市场是复杂的动态系统，受到冲击后一些在正常条件下隐藏的风险可能显现。多重分形能够反映金融系统的复杂性，而普遍认为危机发生时系统复杂性增加，因此理论上可利用多重分形模型分析资产收益或波动的多标度行为来对金融危机进行早期预警。

四、多重分形模型的研究优势与不足

金融市场运行受内部因素和外部因素共同作用，但影响机制尚不明晰，金融时间序列的多重分形特征有助于揭示金融市场复杂性和动态变化情况。MMAR模型是由分数布朗运动复合时间的多重分形变形，分数布朗运动可以反映金融数据分布上的长记忆性。与同样可以体现时间序列长记忆的GARCH(FIGARCH)模型相比，MMAR模型能更有效地刻画数据的标度性质，并且解决了FIGARCH模型的无穷维ARCH参数和标度不一致问题；与GARCH族模型、几何布朗运动等方法的模拟比较，以及利用汇率数据的实证研究结果都说明MMAR模型能更好地体现金融数据特征。Günay利用4个新兴市场(克罗地亚、希腊、波兰和土耳其)股票指数收益日数据将4个GARCH模型(GARCH、EGARCH、FIGARCH、MRS-GARCH)和MMAR模型进行比较分析，结论表明MMAR模型拟合数据的偏差最小[15]。

MSM模型侧重反映金融时间序列的波动，设定形式允许波动率在多个状态分量之间转换，比通常的马尔科夫转换过程更灵活。Calvet等将MSM模型与GARCH、MSGARCH模型进行比较，认为MSM模型能更好地刻画金融时间序列特征[6]；Liu和Lux利用股票指数、汇率和美国国债固定利率债券组合数据的分析发现，二元MSM模型比二元DCC-GARCH模型有更强的预测能力[16]；Ben等利用全球道琼斯伊斯兰市场世界指数日数据的实证分析认为，MSM模型比FIGARCH和FITVGARCH模型拟合数据的能力更强[17]。

MRW与MMAR模型具有一定联系，根据Muzy和Bacry、Bacry和Muzy的研究，MRW模型设定中的连续时间可以看作对数正态多重分形测度中布朗运动的时间变形，因此MRW模型可以改写成与MMAR模型类似的表达形式[18-19]。Duchon和Robert从理论上推导出MRW模型基础上波动率预测和期权定价的解析式[20]；Kutergin和Filiminov(2015)认为MRW模型是唯一具有多重分形性质和高斯无穷小增量的连续随机平稳过程，能够刻画数据分布上的厚尾、波动率集聚、长记忆性、多重分形等6个特点，并且通过Monte-Carlo模拟可将MRW模型应用于期权定价。

多重分形模型的问题主要体现在建模难度较大，算法选取没有明确标准以及估计方法的复杂性等方面。MMAR模型的时间变形是通过乘法级联得到的多重分形测度，根据生成方式不同，主要有对数正态连续级联、二项和Poison分布级联三种形式，但关于它们各自的适用范围和选取标准还没有一致性的结论。MSM模型中波动分量个数不超过5时可以采用最大似然估计法，但当分量个数超过5时，由于转移矩阵维数过高需要采用其它方法才能进行估计，比如粒子滤(Particle filter)方法。一些多重分形随机过程都与MRW模型有联系，这一方面增加了随机游走模型理论上的复杂性，另一方面在特定情况下可以用更易估计的模型来代替随机游走模型，从而使得MRW模型的应用偏少。

五、总结与展望

金融时间序列的分形特征说明资本市场复杂、无规律变化的表象下一些行为是有规律可循的。本文对当前应用较广泛的三种多重分形模型特点及其在金融风险领域的应用现状进行了综述，发现实证研究中风险指标是否考虑数据的多重分形特征对于风险预测结果具有显著影响，基于多重分形模型的风险指标估计、风险预测比基于GARCH族模型的结果更准确。多重分形模型在金融风险研究中的应用还处于深入发展阶段，我们认为未来可以从以下几方面进行尝试与探索：

1.MMAR模型通过将分数布朗运动与时间变形复合来反映金融数据分布的长记忆和多重分形，但分数布朗运动捕捉肥尾的能力相对较弱，未来可以考虑将MMAR模型与刻画尾部极端变化的方法，比如POT方法相结合。

2.将MSM模型与体现多变量之间相关性的方法结合也是一个发展方向，可以在现有的Copula-MSM模型基础上继续进行拓展；MRW模型在风险管理上的应用较少，能否将其他两个模型下的VaR研究方法推广到MRW模型也是值得讨论的问题。

3.目前多重分形模型主要用于分析资产收益市场风险指标VaR，有研究用MMAR模型分析投资组合的风险，最近MSM模型也被用来预测投资组合市场风险，未来可以尝试将多重分形模型应用于资产配置和投资组合风险的估计与预测。