基于带偏倚最大间隔二值矩阵分解的多值矩阵分层填充
2019-03-13胡胜元陈盛双
胡胜元,陈盛双,谢 良
(武汉理工大学 理学院,武汉 430070)
1 引 言
对于部分元素已知的矩阵M,如何通过已知元素重构矩阵M′,使得M和M′尽量接近的问题就是矩阵填充问题.基于特征的协同过滤也可以看作矩阵填充,在协同过滤中,Y是一个m×n的评分矩阵,m是用户数,n是项目数,且Y只有部分元素已知,即只存在部分用户对部分项目的评分,协同过滤的目标就是要预测出用户对其它项目的评分,从而完成对于矩阵Y的填充[1].矩阵分解是解决矩阵填充问题的一个重要方法,它通过已知的评分数据来学习出用户的潜因子矩阵Um×k和项目的潜因子矩阵Vn×k,使得UVT和原矩阵Y在已知元素位置处尽量相等,并根据UVT来对未知评分数据作出预测.
近年来,矩阵分解在国内外得到了广泛研究.D.D.Lee等提出了非负矩阵分解算法[2](NMF),即使得U和V中的所有元素都大于0;B.Sarwar等提出了用奇异值分解来进行矩阵分解[3];N.Srebro等则提出了最大间隔矩阵分解(MMMF)来解决稀疏多值有序评分矩阵的填充问题[4].自从MMMF被提出以来,便引起了很多研究者的关注.
在二值评分矩阵中,评分数据的取值为+1(表示喜欢)或-1(表示不喜欢).每个项目的潜因子向量(V的对应行)可以看成k维特征空间中的一个点,用户的潜因子向量(U的对应行)可以看成该k维空间中的一个超平面,该超平面就将项目的评分数据点分成了二类.MMMF的目标就是学习到表示用户的超平面和表示项目的k维空间中的点,使得每个用户对应的超平面能将这些项目的点分隔开来,从而对未知评分数据进行预测.但是这样的二值分类过程中用户的超平面必须要过k维空间中的原点,这样的超平面并不一定是最优超平面,可能会影响协同过滤的效果.
在多值评分矩阵中,评分可能为 {1,2,…,R},它不同于二值评分矩阵,不能简单的用一个超平面将数据进行分类,解决该问题就必须要解决多分类问题.N.Srebro等提出了多值矩阵下的MMMF[5],将hinge函数成功用于分解多值评分矩阵,除了求解U和V,还需要求解阈值变量θm×(r-1),但是这样对每个用户构造多个超平面,不能够保持最大间隔这一性
质[1].Vikas Kumar等于是提出了HMF[1],通过多次运用二值矩阵下的MMMF,对多值评分矩阵进行了填充.
本文所做的主要工作是首先针对传统的最大间隔二值矩阵分解中存在的用户超平面过原点的约束问题,添加偏倚量γ,将二值矩阵分解成U,V,γ三部分,来对二值评分矩阵进行填充,然后将该方法扩展到处理多值评分矩阵,实现对多值矩阵的填充.最后在真实的多值评分数据集Movielens上实现所提出的填充方法,并将其与类似算法进行比较,从第6节的实验结果中可以看到,本文所提出的方法优于现有的其它算法.
2 相关工作
矩阵分解的主要目标是使重构后的矩阵UVT和原矩阵Y在Y中已知元素处尽量接近.文献[2]为了使UVT更接近原矩阵Y,增加了潜因子矩阵U和V中的元素非负这一约束条件,它的基本思想就是通过最小化已知元素值和UVT中对应的预测值差值的平方和来学习得到因子矩阵U和V.文献[3]通过奇异值分解来学习得到因子矩阵U和V,令Y中未知元素全部为0,从而得到一个稀疏矩阵,再通过SVD对该稀疏矩阵进行分解,虽然该方法可以适当减少原矩阵Y的维度,但是SVD在稀疏矩阵上面会面临很严重的过拟合问题.N.Srebro等在文献[4]中提出的MMMF则用U和V的Froebenius范数最小化来代替矩阵秩的最小化,可以证明MMMF其实是一个半定规划问题,并且能用标准的半定规划求解方法来求解.但是现有的半定规划求解方法只能求解矩阵Y的秩较小时的MMMF问题,因此文献[5]提出Fast MMMF,扩展了hinge损失函数,用梯度下降法来求解MMMF,使其可以解决多值评分矩阵的填充问题,并对不同的损失函数进行了研究.此外,文献[6]也提出了最大间隔的分类方法,并对强泛化和弱泛化进行了讨论.自从文献[5]发表以来,Fast MMMF成为一个重要的研究课题,[7-10]对该方法其后进行了进一步的研究.同时,MMMF也引起了部分研究者对二值评分矩阵的兴趣[11,12],但是他们都把它作为离散值评分矩阵分解的一个特例进行研究.文献[13]基于近似支持向量机提出了PMMMF,提高了矩阵分解的速度.文献[14]则根据相似用户和相似项目,将原矩阵分割成多个子矩阵,进而对每个子矩阵分别进行分解.文献[1]则多次对二值矩阵使用MMMF,从而实现对多值评分矩阵的填充.也有很多学者采用低秩矩阵分解对多值矩阵进行填充,从而进行个性推荐,他们大多是对用户或者项目的一些特性以及相似性的度量上作了许多改进,如文献[15]将用户的评分信誉进行分组,来识别评分矩阵中的虚假评分,从而提高矩阵填充结果;文献[16]则添加项目的热门因子,对皮尔逊相似性进行优化,从而提高推荐效果.
3 矩阵分解
假设Y是一个m×n阶的用户-项目评分矩阵,yij∈{1,2,…,R}表示第i个用户对第j个项目的评分,yij=0表示第i个用户未对第j个项目进行评分,即为Y中的未知元素.矩阵分解的目的就是将部分元素已知的矩阵Y∈Rm×n分解成矩阵U∈Rm×k和V∈Rn×k,使得Y≈UVT,其中k是矩阵U和V的秩,也即是我们的潜因子个数,它远小于m和n.
UVT可以看成是矩阵Y的一个低秩逼近.Ui表示U的第i行,它是第i个用户的潜因子向量,Vj表示V的第j行,它是第j个项目的潜因子向量.在低秩矩阵分解中,最终目的就是要找到满足Y≈UVT的秩最小的U和V.矩阵分解问题其实就是一个优化问题,它的目标函数是:
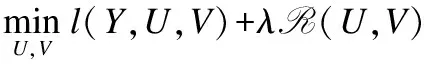
(1)
其中Y是原评分矩阵,l(·)是损失函数,用来衡量Y和UVT的相近程度,R(·)是正则函数,保证U和V具有低秩性,防止过拟合,λ为正则系数.如果l(·)和R(·)都为凸函数,则该问题可以有效求解.常用的损失函数有平方损失函数[17],似然损失函数[18],以及hinge损失函数[5].
矩阵分解问题其实也是一个以Ω={(i,j)|yij≠0,∀yij∈Y}为训练集的有监督学习问题,它必须避免过拟合问题,因此目标函数(1)又可以写成(2):
(2)
Fazel发现也可以用核范数来代替正则函数来防止过拟合[19],即目标函数(1)也可以写成(3):
(3)
其中‖UVT‖Σ是UVT的核范数,它等于UVT的所有奇异值之和.但是‖·‖Σ是一个复杂的不可微函数,最优化问题不容易求解,因此文献[19]定义了一个和核范数等价的函数,目标函数(3)可以重述为:
(4)
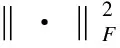
4 带偏倚最大间隔二值矩阵分解
假设Ym×n是一个二值评分矩阵(m为用户数,n为项目数),其中用户对项目的评分为+1和-1,+1表示喜欢,-1表示不喜欢,因此二值评分矩阵的预测问题可以看成是一个二分类问题,对于每一个用户而言,所有项目可以分为两类,一类标记为+1,表示喜欢,另一类标记为-1,表示不喜欢.若将项目j表示成k维空间中的一个点Vj∈R1×k,则用户可以看成是k维空间中的一个超平面,它将k维空间中的这n个点分隔在超平面两侧,一侧是标记为+1的一类,另一侧是标记为-1的一类.由于每个人的喜好不相同,他们对每个项目的分类结果也不同,则每个用户表示的超平面也不同.根据每个用户k维空间中的这n个点和已知的分类结果,可以学习到每个用户的超平面.
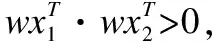
在Ym×n中,如果某个用户未对某一项目进行评分,令其对应位置元素为0,即yij=0,则观测集可以用Ω={(i,j)|yij≠0,∀yij∈Ym×n}来表示,它是有评分的用户和项目对的集合.令X=UVT,表示经过分类学习重构后得到的评分矩阵,为保证用户对每个项目的分类尽量准确,对任意的(i,j)∈Ω,需要令yij和xij同号,即yijxij>0.但是当xij=0时,无法判断用户对项目的喜好,因此还需要加入硬间隔为1的约束,即yijxij>1,使得xij尽量不为0.
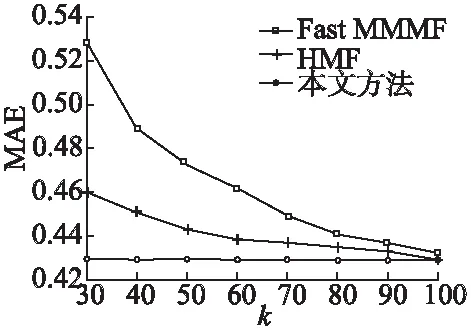
为了衡量分解的好坏,需要构造一个损失函数h(·),当分解效果越好时,函数h(·)的值尽量越小.当yijxij>1时,分解效果最佳,所以函数h(·)必须满足h(yijxij)=0这个条件;而当0 (5) 然而这种分类器将用户i的超平面定为UixT=0,该超平面必经过k维空间中的原点(0,…,0)T,但有时经过原点的超平面并不具有最好的分类效果.图1是支持向量机中两个不同的分类器L1和L2对二维数据的分类情况,L1经过了原点,而L2没经过原点,从图中可以看出分类器L1对样本数据的分类结果没有L2的效果好.这说明经过原点的分类器并不一定是最优的. 图1 不同超平面分类器下分类结果Fig.1 Classification results under different hyperplane 因此对每个用户的超平面进行一定的偏倚量γ,将用户i的超平面定为UixT+γi=0,其中Ui和γi共同决定用户i的超平面,需要根据已观测的数据对Ui和γi进行学习.对任意的(i,j)∈Ω,不再是令yijxij>0,而是令yij(xij-γi)>0.同时任然保持最大间隔的约束,即yij(xij-γi)>1,损失函数采用hinge函数,则整体的损失函数l(·)为 (6) 同时为了防止模型的过拟合,正则化函数中还应该加入γi的正则约束,即 (7) 其中γ=(γ1,…,γm)T.则矩阵分解问题的目标函数为: (8) 最终将矩阵Y分解成U,V,γ三部分.由于hinge损失函数在每个点处可导,正则函数也可导,所以可以用最速梯度下降法对该优化问题进行求解,其中目标函数J对Uip、Vjp、γi的导数分别为: (9) (10) (11) 则可以用交替优化的方法分别更新U、V和γ,其中每个元素的迭代公式分别为: (12) (13) (14) 其中c为迭代步长. 当上述最优化问题求得近似解U,V,γ后,根据以下分段函数对二值评分矩阵进行预测: (15) 多值评分矩阵填充问题可以看成一个多分类问题,目前解决多分类问题的方法主要有两种,一种是直接构造一个多分类目标函数,建立一个多分类器;另一种是将多分类问题拆解为若干个二分类问题,建立多个二分类器,然后将二分类的结果进行组合. N.Srebro提出的FastMMMF[5]是通过构造多分类目标函数来解决多值评分矩阵预测问题,虽然该方法比其他类似的方法效果要好,但是同一个用户具有多个平行的超平面来分类,当超平面间的间隔较小时,这种分类的方法不能保留最大间隔这一特性.而Vikas Kumar提出的分层矩阵分解(HMF)[1]则是多次对二值评分矩阵进行分解,逐次对评分进行预测,从而完成多值矩阵的填充.下面介绍采用上节中提出的改进的最大间隔二值矩阵分解方法和HMF方法完成多值矩阵的分层填充. (16) (17) 本文提出的解决多值矩阵的分层填充方法如表1中的算法所示,并且在下节中在真实数据集上验证了算法的有效性. 表1 算法伪代码 算法1.带偏倚最大间隔二值矩阵分解对多值矩阵分层填充算法输入:观测的数据矩阵Y,潜因子个数k,正则系数λ输出:填充后的数据矩阵^Y1 for q=1 to R-12 根据公式(16)计算Yq3 初始化Uq,Vq,γq4 do5 交替优化根据公式(12)更新Uq6 交替优化根据公式(13)更新Vq7 交替优化根据公式(14)跟新γq8 until J收敛9 根据公式(15)计算^Yq10 根据公式(16)预测^yij=q的元素位置11 end12 根据公式(16)预测^yij=R的元素位置13 返回矩阵^Y 为了验证基于改进的最大间隔二值矩阵分解的多值矩阵填充方法对于多值评分矩阵预测的有效性,本文在Movielens 1M数据集上进行数据实验.其中Movielens 1M包含了6040个用户对3952个电影的累计1000209个评分,评分的取值为{1,2,3,4,5},其中3706个电影有用户评论,并且每个用户最少评论了20个电影. 图2 不同λ值对应的ZOE值对比Fig.2 Different ZOE values for different λ λ的取值对矩阵分解问题至关重要,适当的λ值可以防止模型过拟合.本文在进行矩阵分解时所有步骤的λ均相同,为了得到最合适的λ值,本文在二值矩阵Y3上进行实验,从Y3非0元素中随机选取20%作为测试集,剩余的作为训练集,计算每一个λ对应模型的ZOE值,其中ZOE值表示预测的错误率,其计算公式如下所示: (18) (19) 本实验采用矩阵分解领域中常用的两种实验方法:弱泛化与强泛化来检验本文方法的有效性. 弱泛化实验:先随机选取5000个用户的所有评分数据,再从该评分数据集中随机选取20%的元素作为测试集,将剩下的80%的元素作为训练集,然后用训练集中的元素对模型进行训练,当模型训练好后,再对测试集中的元素进行预测,并与测试集中的真实评分结果进行比较. 强泛化实验:分为两个步骤,第一步随机选取5000个用户的评分数据,用于训练初始预测模型,第二步将剩余用户的数据作为测试集,再从测试集中随机选取20%的评分元素组成集合H,剩余的组成集合G,将训练好的初始模型在G上稍作调整,然后对H中的元素进行预测,并与H中的真实评分结果进行比较. 本实验选取的评价指标为平均绝对误差MAE,它用来衡量预测评分与真实评分之间的偏差,MAE值越小表示预测结果越好,其计算公式如下所示: (20) 其中Ω1为测试集.本文与目前最新的方法进行了比较,参与比较的算法有URP[20]、Attitude[20]、Fast MMMF[5]、E-MMMF[7]、PMF[21]、BPMF[22]、GP-LVM[23]、iPMMMF & iBPMMMF[9]、Gibbs MMMF & iBPMMMF[10]和HMF[1],同时为了方便比较,将每个算法得到的MAE值同除以1.6[1]. 表2 不同算法的MAE值比较 算法弱泛化强泛化URP0.4341±0.00230.4444±0.0032Attitude0.4320±0.00550.4375±0.0028Fast MMMF0.4156±0.00370.4203±0.0138E-MMMF0.4029±0.00270.4071±0.0093PMF0.4332±0.00330.4413±0.0074BPMF0.4235±0.00230.4450±0.0085GP-LVM0.4026±0.00200.3994±0.0145iPMMMF & iBPMMMF0.4031±0.00300.4089±0.0145Gibbs MMMF & iPMMMF0.4037±0.00050.4040±0.0055HMF0.4019±0.00440.4032±0.0022本文方法0.4005±0.00140.3986±0.0085 在实验过程中所有算法的潜因子个数都取为100,将弱泛化和强泛化分别进行三次实验,取三次实验结果中的MAE的最大值和最小值作为实验结果,得到本文方法以及其他方法的MAE值见表2. 从表2中可以看出,本文的方法在Movielens 1M数据集上,无论是弱泛化实验还是强泛化实验,MAE均值都小于其他方法,表明本文方法对评分矩阵预测的准确率都要比其他方法略高,验证了本文方法的有效性. 潜因子个数k的取值对评分矩阵预测的准确率有着重要影响,当k取值较小时,特征空间维数较小,不能完整表达出用户和项目的信息;当k值较大时,进行矩阵分解的计算复杂度成几何倍数增长,影响矩阵分解求解.为了确定本文方法中k的取值的影响程度,本文在数据集Movielens 100K上进行实验.Movielens 100K数据集包含了943个用户对1682个电影的累计100000个评分,评分的取值为{1,2,3,4,5},且每个用户最少评论了20个电影. 图3 不同k值下的MAE值比较Fig.3 Different MAE with different k 在实验中随机选取80%的评分数据作为训练集,剩余20%作为测试集,计算不同k值下,取最优的λ值时所对应的MAE值,同时计算Fast MMMF和HMF方法下的MAE值与之比较,其中k的取值为{30,40,50,60,70,80,90,100},得到不同k值下三种方法的MAE值对比图,见图3. 从图3中可以看出,当k值减小时,Fast MMMF的MAE值变化非常巨大,表明Fast MMMF方法中特征表示空间维数很大,不利于算法的扩展性;HMF的MAE值变化比较平缓,在较适中的特征空间中可以进行问题求解;而本文提出的方法的MAE值基本上无变化,表明本文方法在较小的特征空间中就能够完成问题求解,且具有较高的分解效果.因此本文的方法可以保证在不降低准确率的情形下进一步减少潜因子个数,从而提高矩阵填充的速度. 本文对传统的最大间隔二值矩阵分解方法进行了改进,并将其运用到多值评分矩阵的填充问题,实验表明,本文提出的方法对多值评分矩阵预测的准确率优于其他方法,同时本文提出的方法能够将矩阵分解在一个较低维度特征空间中进行,能在保证预测准确率基本不变的前提下,提高矩阵分解速度,并大幅减少计算过程中的空间占用. 本文提出的方法在进行多次二值矩阵分解时,采用了相同的正则系数λ和潜因子个数k,这可能会导致这两个模型参数不能够很好适应不同步骤下的评分矩阵.在今后的工作中我们可以对每次二值矩阵分解单独学习这两个模型参数,以加强矩阵填充的准确率.另一方面,本文提出的方法没有考虑数据的均衡性,在分类问题中,不同类别样本数据的不均衡可能会引起分类器更加偏向于某一类,从而导致分类器不能很好地适应新数据,出现大量的错分类的情况.在未来的工作中,我们会对这一类问题进行研究,使得模型有更好的鲁棒性,能够不受数据不均衡性的影响.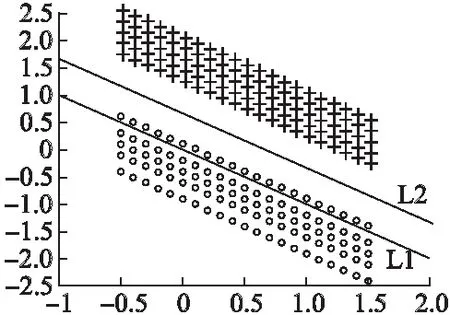
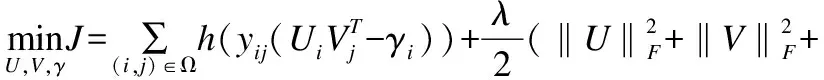
5 多值矩阵的分层填充
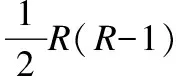
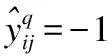
Table 1 Algorithm pseudo code
6 实验及分析
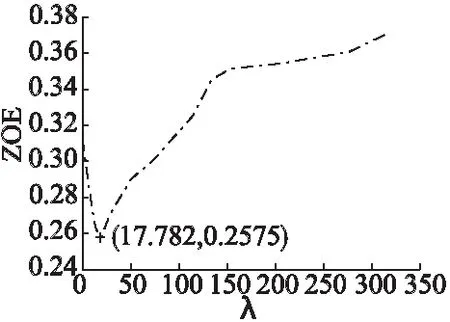
6.1 关于正则系数λ的选取研究
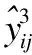

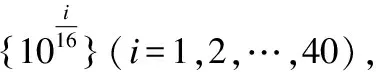
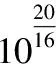
6.2 本文方法与其他方法的MAE值比较
Table 2 Different MAE in different algorithm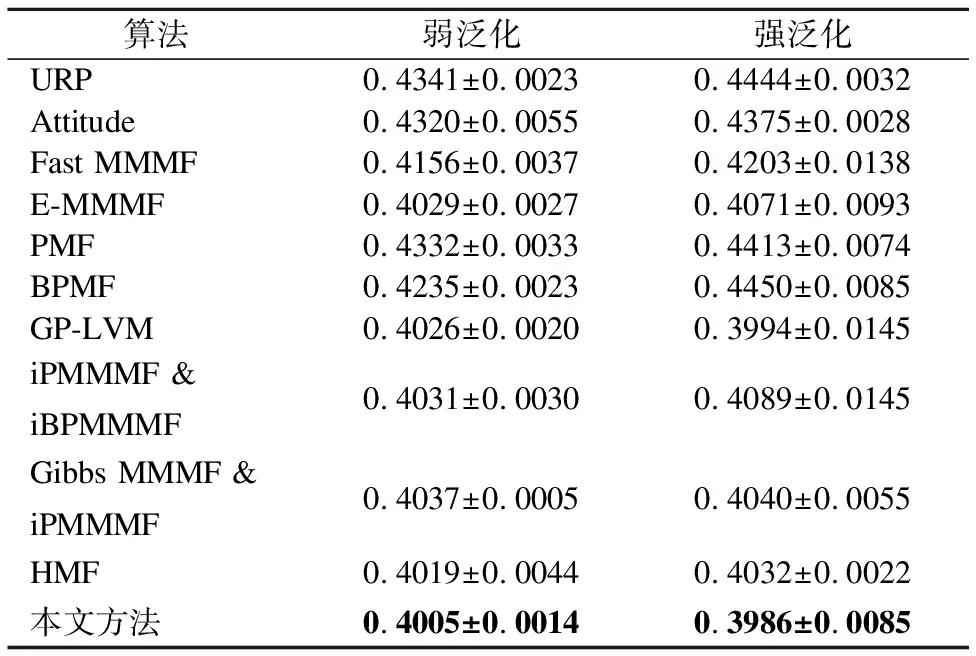
6.3 关于潜因子个数的分析
7 总结与展望
