战术导弹气动伺服弹性滑模控制技术

2019-03-13张公平段朝阳赵艳辉郑鹍鹏

导航定位与授时 2019年2期

张公平，段朝阳，赵艳辉，郑鹍鹏

(1.中国空空导弹研究院，洛阳 471099；2.航空制导武器航空科技重点实验室，洛阳 471099)

0 引言

自可控飞行器诞生以来，气动伺服弹性(Aeroservoelasticity，ASE)就一直是飞行控制系统设计必然面对的难题之一。针对不同用途的战术导弹，国内外相关研究机构设计了形式各异的ASE控制算法，其原理多采用被动式滤波。根据中心频率设计陷波器，从一定程度上缓解了ASE的不良影响，但同时也带来了系统的鲁棒自适应问题，即引入结构滤波器的闭环系统在弹体弹性模态时变特性难以精确建模的现实条件下，经常出现飞行状态振荡、执行机构饱和，甚至操纵失稳等现象[1-4]。

近年来，为适应空天一体作战、突破敌防御系统、快速精确打击等任务需求，普遍要求导弹结构轻量化，以使其具备高速、高过载与远射程能力。然而，在高速飞行时，轻量结构在外界激励下，更易发生弹性振动，并导致控制异常。以美国某空空导弹项目为例，其前期试飞遭遇了严重的ASE问题。分析认为，弹体弹性振动信号进入飞行控制系统后，被舵机高频响应，气源消耗殆尽，导致舵不跟随，从而引发弹体失控翻滚[5]。因此，需要引入结构滤波器，并使其参数随弹体结构特性变化。为准确获取实际飞行过程中的弹体结构特性，常采用在线辨识技术[6-8]。

随着传感器带宽及舵机性能的进一步提高，弹体弹性振动更容易被敏感并被响应，导弹ASE问题更加凸显。本文通过建立某战术导弹高精度耦合弹性动力学模型，针对其时变特性，设计了自适应结构滤波器。然后，在经典三回路控制架构下，采用极点配置方法自动优化增益，并对主增益设计局部切换面进行二次调节，从而实现弹性弹体的滑模变结构控制，改善系统鲁棒性。最后，通过联立刚体动力学模型，对导弹ASE控制技术进行非线性仿真验证。

1 导弹气动伺服弹性动态建模

1.1 弹性基准坐标系定义

为描述弹体结构弹性变形程度，定义弹性基准坐标系如图1所示。

图1 弹性基准坐标系示意图Fig.1 Schematic of elasticity reference coordinate frame

图1中，O0X0Y0Z0即为弹性基准系，其三轴分别与弹体系OX1Y1Z1三轴平行。

1.2 高精度耦合动态建模

长细比较大的战术导弹在法向力作用下，振动方程如下：

(1)

其中，EJ(x)为弹性基准系某截面x处的抗弯刚度，m(x)为线密度，Wy(x,t)为法向力。则基于模态叠加与变量分离原理[9]，可设弹性变形量为：

(2)

式中，φi(x)为第i阶振型，qi(t)为对应的广义坐标。

在两端自由梁假设及零初始条件下，将式(2)代入式(1)，整理可得广义坐标方程：

(3)

式中，ξi为结构阻尼比，ωi为固有振动频率，Qi为广义力，广义质量为：

(4)

若考虑气动力、舵控力与舵惯性作用，则广义坐标方程右端项写成广义加速度的形式为：

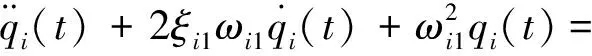
(5)

其中，各系数定义如下：

(6)

式中，α与ωz所在项代表了刚体转动与弹性振动的耦合影响。

1.3 线性动态建模

考虑到现有技术对分布式气动特性的预测精度与非线性仿真可信度的需求，对式(5)作简化处理，并进行Laplace变换，可得由弹性振动引起的俯仰角速率及加速度对舵偏的传递函数为：

(7)

其中，xg与xa分别为速率陀螺与加速度计的安装位置，Ci与Di分别为舵控力与舵惯性的影响。根据试飞数据的辨识结果可知，结构振动与飞控系统的耦合特性主要受集中力影响[9]。

2 模态自适应结构滤波器设计

在实践中，结构滤波器设计与系统稳定裕度校核之间的关系如图2所示。

图2 弹性稳定裕度校核流程示意图Fig.2 Flow diagram of stability margin verification

针对弹性弹体的增益稳定，常采用凹陷结构滤波器[10]，利用其高频零点与弹性弹体的高频极点对消，形式如下：

(8)

其中，ωp越小滤波器的宽度越大，但在低频段引起的相位滞后也越大，而ξp的影响则相反。通过选择ξp与ωp的值，既可使系统的频率特性不发生较大改变，又能保证系统在滤波后具有较好的幅值裕度和相位裕度。

以某导弹一阶弯曲振动模态为例，其结构阻尼比为0.05，根据发动机推进剂燃烧程度随时间变化情况，设计结构滤波器主要参数的自适应规律具有如下形式：

(9)

其中，T01为主动段与被动段的时间分界点。

3 局部增益滑模控制器设计

在伪攻角反馈三回路自动驾驶仪中，引入局部增益滑模控制策略以抑制系统性能对指令幅值及其他干扰的灵敏度，同时考虑弹体弹性影响，可以得到控制结构如图3所示。

控制系统设计时，可先确定刚性弹体的控制增益Id、K0与K4，并设计结构滤波器；然后引入局部增益滑模控制策略，利用切换函数，实现对加速度误差积分增益的变结构控制。

图3 导弹气动伺服弹性滑模控制结构Fig.3 Topology of ASE sliding mode control for missile

3.1 控制增益自动优化

对于大包线飞行的战术导弹而言，基于试错原理的系统参数整定工作量较大，且存在不可避免的品质离散问题，不利于导弹性能潜力的充分发挥。为此，可采用极点配置理论[11]，对刚性弹体伪攻角反馈三回路自动驾驶仪进行优化设计。在舵控处断开得到系统的开环传递函数为：

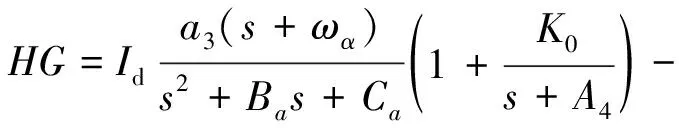
(9)

其中，

由此得系统的三阶闭环传递函数为：

(10)

若将极点配置到由参数A、ω、ξ所决定的期望位置处，则有式(11)成立：

(s+A)(s2+2ξωs+ω2)=

s3+(Ba+Ida3-IdK4va5)s2+

(Ca+Ida3ωα+IdK0a3-IdK4va5a1)s+

IdK4va5Cz

(11)

推导可得控制增益为：

(12)

其中，共轭极点频率为：

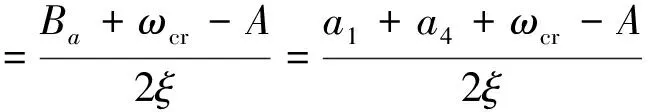
(13)

3.2 滑模控制策略设计

将阻尼回路与增稳回路等效为传递函数：

(14)

其中，

则等效控制结构如图4所示。

图4 等效控制结构Fig.4 Equivalent control structure

其中，c2>0,c1>0。

将系统动态约束方程代入切换面函数的一阶导数整理可得：

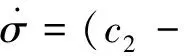
(15)

选择Lyapunov函数为：V(σ)=σ2/2。

在Lyapunov稳定性条件下有滑模控制策略：

(16)

针对切换面函数中角加速度信号可能带来的噪声问题，可采用滤波器对角速度和角加速度进行估计[12]，并定义等效切换面函数：

σeq=e-K6yωsynth

(17)

其中，

进一步整理可得实用的滑模控制策略为：

(18)

4 ASE控制技术仿真

气动伺服弹性会使控制系统稳定性降低，加之多种非线性环节如舵系统间隙与饱和等因素影响，经常导致飞行状态剧烈振荡，甚至失控。因此，有必要在地面仿真试验中集成ASE模型，如图5所示，以检验控制系统的有效性。

图5 非线性ASE仿真系统原理图Fig.5 Schematic of nonlinear ASE simulation system

在飞行高度10km，速度2.0Ma，攻角20°的某特征点处，动力系数a2=16.9259，分别采用经典线性与滑模变结构方法，针对标称模型进行控制设计，在a2向下摄动5倍的条件下进行仿真，结果如图6所示。

图6 动力系数a2摄动条件仿真对比Fig.6 Simulation comparison with perturbation of dynamical coefficient a2

可见，带有滑模变结构策略的控制系统性能明显优于经典线性控制，在保持快速性的同时，超调与稳态品质优势显著，鲁棒性更强。

对一条高度约为20km的高空弹道进行非线性仿真，与试验结果的对比如图7所示。

图7 ASE仿真与试验结果对比Fig.7 ASE simulation comparison with testing results

可见，对于长时振荡现象，本文所提仿真方法能够较为准确地复现时长。而且，采用离散傅氏变换的快速算法(Fast Fourier Transformation，FFT)技术对试验数据进行频谱分析，对比数字仿真ASE振荡频率偏差不大于0.5Hz，幅值吻合较好，且与典型ASE现象的持续时间基本吻合，满足控制系统验证对ASE仿真预测的要求，证明了在非线性仿真系统中集成弹体弹性模型是合理的。

为抑制ASE对高空弹道飞行状态的不良影响，采用本文提出的自适应滤波与滑模控制技术进行数字仿真，结果如图8与图9所示。