一种基于虚拟导航点的超低空飞行器威胁回避算法研究
2019-03-13尹明新
尹明新,姜 伟,孙 骞
(1.四川航天系统工程研究所, 成都 610100;2.零八一电子集团科技公司, 成都 611731;3.哈尔滨工程大学, 哈尔滨 150001)
0 引言
超低空飞行技术是提高亚声速无人飞行器生存和突防能力的重要手段。该技术可有效利用地形和地杂波的掩护,大幅降低飞行器被探测到的概率,增大敌方防御系统的拦截难度。其中,地形跟踪、地形/威胁回避技术的发展是超低空飞行的关键[1]。
目前,具有地形/威胁回避功能的飞行器,主要是通过事先规划好的飞行走廊实现地形回避的。但在实际飞行过程中,常常会发生一些突发的状况,出现先前未探测到的威胁,如探测雷达、敌方拦截飞机的来袭等。另外,在工程应用中也遇到了一个很大的问题,就是障碍物图的保障,飞行走廊内一些细小的障碍物信息(如高压线、杆塔、线塔等),无法通过数字高程图和现有的障碍物保障图来获取。这些情况的出现,使得预先设定的航迹很有可能会穿越未知威胁的作用区域,造成飞行器的风险系数骤然增大。因此,生存和突防要求迫使超低空飞行器必须具备自主威胁回避的能力。
常用的地形/威胁回避算法有梯度法[2]、启发式搜索算法(A*算法)[3]、动态规划法[4]、遗传算法[5]等,但这些常用于离线的地形/威胁回避航迹规划[6],普遍存在计算量大、易陷入局部最优等问题。针对突发威胁的情况,现阶段仍没有一个比较成熟且可直接工程应用的自主威胁回避算法。
近年来,基于被动雷达无源定位的自主探测技术使得飞行器逐渐具备了威胁感知的能力[7],同时国内外利用前视序列图像实现障碍物检测和距离解算的技术研究已经取得了一定成果[8]。本文以自主探测为基础,结合超低空无人飞行器的飞行特点,提出了一种基于虚拟导航点的威胁回避算法。该算法设计简单,计算量小,易于实现,能够有效保证飞行器在超低空飞行走廊中的安全。
1 问题描述
超低空飞行走廊是立足于预先或者当前已经掌握的所有战场环境信息,采用全局最优规划方法离线获得的。在现代战争中,由于战场态势瞬息万变,矛与盾之间的对抗程度越来越强,加上超低空无人飞行器多为亚声速巡航,在长时间的飞行过程中威胁环境和预定任务的形态都极有可能发生变化,飞行器的突防难度变得越来越大。另外,在预定规划的超低空飞行走廊内,还可能存在通信信号塔、高压线塔、高压线等障碍物[9],这些障碍物的高度有些可达百米级,并且在航迹规划时该类障碍物的信息很难全面获取,这给飞行器超低空飞行的安全带来了极大威胁。在这些情况下,离线规划出的最优航迹已不能满足任务需求。因此,对飞行器面对突发威胁时的自主回避问题的研究是十分迫切且具有重要意义的。
随着现代信息技术和传感器技术的不断发展,基于视觉、雷达的感知手段层出不穷,在线数据获取、传递以及自主探测技术使飞行器逐渐具备了强大的环境感知能力。同时,计算机快速处理技术和海量存储技术的快速发展使得无人飞行器具备了自主智能飞行的可能[10]。
面对突发威胁时能够进行自主回避是亚声速超低空无人飞行器自主飞行的重要特点。本文研究的无人飞行器利用射频传感器及红外探测器进行自主飞行,具有探测未知威胁和障碍的能力,可在飞行过程中及时发现处于航线上的威胁,并甄别威胁类型。其中射频传感器可识别防空雷达等威胁的位置和作用距离,红外探测器可识别电线塔、烟囱等障碍物的距离及大小。本文以此为前提,针对预定飞行走廊内的某一范围区域环境发生改变(如发现预定航迹上存在探测雷达、防空火力网、障碍物等威胁)问题研究威胁回避策略。飞行器可以在线改变飞行航迹,对这些区域进行自主回避。
2 基于虚拟导航点的威胁回避原理
无人飞行器自主飞行主要依靠惯性/卫星组合以及其他辅助导航手段,在各导航点之间大都按照直线飞行。下面首先介绍了在直飞航迹上出现突发威胁时基于虚拟导航点的威胁回避原理,定义为方案A(见图1)。

图1 直飞过程威胁回避(方案A)Fig.1 Threat avoidance on straight-flight process (Strategy A)
按照上述原理生成的航迹仍有可能会穿过其他已经探测到,但并不在原航迹上的威胁。因此,本文设计了多条回避航迹,利用不同的偏航距离ΔZi生成不同的虚拟导航点,即N个ΔZi对应N条航迹。最后,再设计回避代价函数(其主要与航程代价、威胁代价以及高度代价相关),N条航迹即对应N个代价函数值,其中对于经过其他威胁的航迹,其代价可以设为无穷大。这样即可在生成的N条航迹中,选择代价最小的一条航迹作为回避航迹。
因为飞行器对威胁的探测距离有限,因此不可能完全发现新航迹A—Ti—B上的未知威胁,尤其在回归航迹TiB及其后面的航迹段。当飞行器按照方案A机动回避时,有可能在转弯飞行过程中发现前方航迹上又出现了新的威胁,该问题本质上可以归结为如何从与回归航向不平行的当前航向又重新回归到原航迹的问题,本文根据当前航向角与回归航向角的大小分两种方案解决。
方案B:在规避航迹C—Ti—B上发现前方航迹存在威胁,即当前航向角小于回归航向角,如图2所示。

图2 机动过程威胁回避(方案B)Fig.2 Threat avoidance on maneuvering process (Strategy B)
假设飞行器在C点探测到前方航迹TiB上存在新的威胁区域,则可以RAi为转弯半径进行侧向机动,直至到达另一个虚拟导航点TAi,此时瞬时航向与回归航向平行,问题又变成了在与原航迹平行的航迹上如何回归的问题,可以按照方案A中回归航迹的计算方法计算出回归航迹TAiD,此时不同的转弯半径RAi将得到不同的虚拟导航点TAi。因此,同样可以通过控制不同的转弯半径RAi在线规划出N条航迹,然后按照回避航迹评价方法选择一条代价最小的航迹即可。
方案C:在回归航迹TiB上发现前方航迹存在威胁,即当前航向角大于回归航向角,如图3所示。
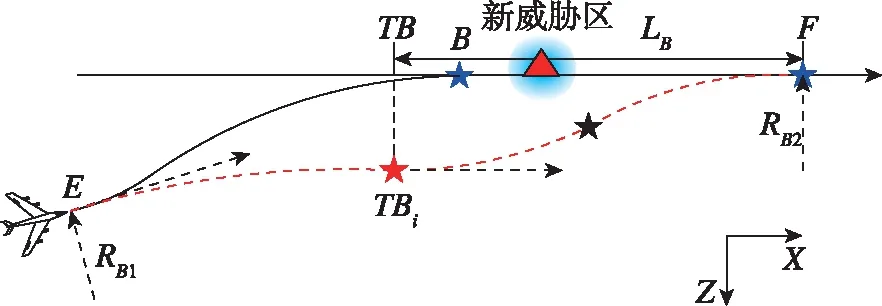
图3 机动过程威胁回避(方案C)Fig.3 Threat avoidance on maneuvering process (Strategy C)
假设飞行器在E点探测到前方航迹存在新威胁区,则可以RBi为转弯半径进行机动,到达虚拟导航点TBi,该虚拟导航点可位于原航迹的任意一侧(取决于RBi的大小和机动方向),此时瞬时航向与回归航向平行,最后再规划出回归航迹TBiF重新回到原航迹。
通过分析可以发现,当飞行器即将贴近原始航迹,即瞬时航向快逼近原航向时,如图4所示,如在G点发现前方直线航迹上又出现新的威胁区,如果仍按照上述方法进行规避,则可能由于航向偏转角的限制,生成的虚拟导航点会很靠近原航迹,偏航距离将非常有限,导致回归航迹将不能使飞行器成功回避威胁。对于这种情况,可以利用探测器的探测范围远比威胁半径大的特点,待飞行器重新回到原始航迹上的B点后,再按照相应的策略重新进行威胁回避。

图4 机动转直飞过程威胁回避Fig.4 Threat avoidance on maneuvering to straight-flight process
本文的方案B和方案C,其本质都是研究如何从与回归航向不平行的当前航迹重新回到原航迹的问题,解决思路都是让飞行器先通过转弯进行侧向机动,直至使当前航向与原航迹所在的回归航向保持平行,然后再按照对应算法生成回归航迹,得到完整的回避航迹。这种思路同样适用于在非直线航迹上规避威胁的问题,解决方法是一致的。
3 算法设计
3.1 基本假设
本文的算法以飞行器具备自主探测威胁的能力为基础,满足以下基本假设条件:
1)射频传感器具备全方位探测能力,能够根据先验信息甄别威胁种类、位置及作用半径。
2)红外探测器可实现障碍物检测,可识别障碍物的距离和大小;受水平视场角(半视场角为α)的限制,探测范围有限;视场中心线水平投影与速度矢量水平投影重合。
3.2 几何解算
利用本文提出的方法自主回避威胁的关键是计算虚拟导航点的位置、飞行器机动转弯半径,同时确定航向偏转角。设飞行器原航迹的航向角为ψ,威胁中心在航迹上的投影为O′,与A点的距离L1≈Rc(可以等效为射频或红外探测距离),设飞行器发现威胁区时的位置为(xs,ys),则O′点的位置为:

(1)
求解虚拟导航点Ti的位置:

(2)
其中,ΔZi为虚拟导航点Ti到原航迹的距离,即偏航距离。考虑到飞行器机动能力限制的因素,本文将AG1段和G1Ti段的转弯半径设计为同一个值R1,由几何关系可以计算机动转弯的2个重要参数:
(3)
其中,θ1为从A点到G1点以及从G1点到Ti点的航向偏转角(即转弯过程对应的圆心角),回归航迹TiB的相关参数同理可求。
式(3)表明,当偏航距离ΔZi一定时,探测距离L1越大,转弯半径R1越大,这是有利于飞行器机动的,即越早发现威胁,则越能以最小的代价避开威胁。当探测距离L1一定时,如果ΔZi
在利用红外探测器进行障碍物回避时,还涉及由最小转弯半径和视场角限制引起的最大航偏距的问题。设飞行器的最小转弯半径为Rmin,则可以根据整条回避航迹求出最大的偏航距离为:
ΔZmax=min(ΔZmax1,ΔZmax2)
(4)
其中,转弯半径越小,偏航距离越大,则由最小转弯半径Rmin,可根据式(3)解算出ΔZmax1;回避航迹上可能出现其他威胁,因此回避航迹应该始终处于飞行器的探测范围内,则由半视场角α,根据图5几何关系,可以解算出由半视场角确定的最大偏航距离ΔZmax2。

图5 视场角与航偏距之间的关系Fig.5 Relationship between FoV-angle and offtrack-range
根据几何关系,可解算出:

(5)
对于当前航向与回归航向不一致的情况,以图2为例,设在规避航迹的C点(xf,yf)发现目标时,飞行器的当前转弯半径为Rf,航向角为ψf,此时根据不同的转弯半径Rfi可以得到虚拟导航点TAi的位置为:
(6)
一旦求解出虚拟导航点TAi的位置后,即可按照相应的算法生成对应的回归航迹。
3.3 回避代价函数
本文设计的威胁回避算法需要根据不同的偏航距离或转弯半径实时解算出N条待选回避航迹,建立对应的代价函数,并从中选择代价最小的航迹,从而有效地规避威胁区域。为了表征回避航迹的综合性能,对各个影响因素按照归一化原则转化为0~1之间的数值,然后再确定各个单项指标在综合指标中的权重,最后得到一个表征回避航迹综合指标的数值。
回避代价主要与偏离原航迹的距离、威胁程度、高度代价(保证地形跟踪性能)相关,据此建立代价函数:
f(l)=w1z(l)+w2t(l)+w3h(l)
(7)
其中,z(l)为虚拟导航点到原航迹的距离,表征航程代价;t(l)为重规划航迹的威胁代价,如果航迹上有新的威胁或障碍,则可取为无穷大;h(l)为高度代价,其表达式为:
h(l)=var(l)+dh(l)+mane(l)
(8)
表征地形跟踪的性能,与离地高方差、平均离地高及纵向机动代价有关。本文根据预测的侧向航迹以及地图高程信息,利用飞行器纵向控制回路特点在线预测对应N条侧向航迹的N条纵向航迹,计算高度代价。w1、w2、w3分别为相应代价的权重。
发现威胁后,在三维空间中预测N条三维航迹。这样即可在N条航迹中,选择出代价最小的航迹作为回避航迹。
3.4 算法流程
根据前面的介绍和分析,图6给出了基于虚拟导航点的超低空威胁回避算法流程。当飞行器在飞行过程中利用自主探测设备发现前方航迹穿过威胁区域后,可根据自身的飞行状态,选择相应的回避策略。
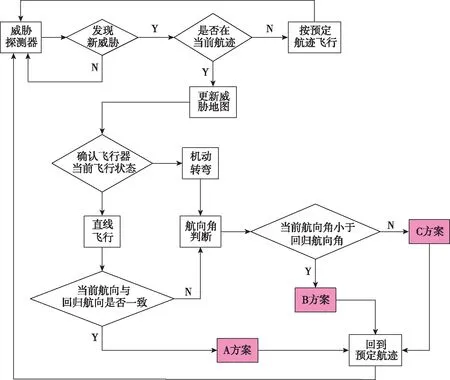
图6 算法流程图Fig.6 Algorithm flow diagram
4 仿真算例
4.1 仿真条件
利用Matlab软件对超低空飞行器威胁回避算法进行仿真。考虑到射频传感器的探测距离较远,回避过程相对简单,本文主要针对红外探测器发现威胁源(障碍物)时的回避算法进行验证。采用随机生成的大小为15km×15km的三维数字地图进行仿真,地图分辨率25m×25m,如图7所示。
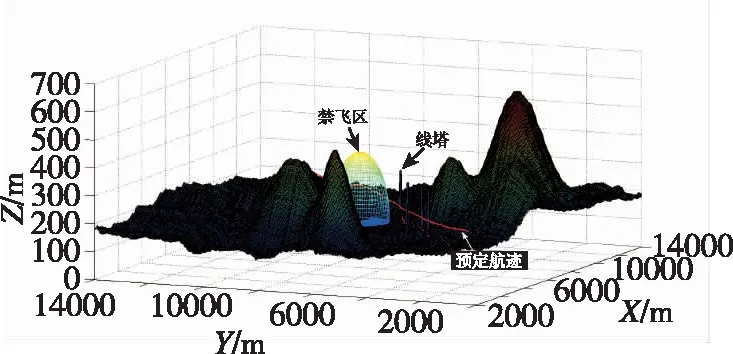
图7 三维数字地图Fig.7 3D digital map
设红外探测器的探测距离Rc=6km,半视场角α=4°;飞行器最小转弯半径Rmin=10km,纵向质心控制回路时间常数τ=7s,安全离地高度h0=50m;地形跟踪最大和最小离地高度分别为100m和20m;代价权重w1=0.2、w2=0.4、w3=0.4;障碍物为1m×2m×150m的线塔,离障碍物的安全距离取40m,仿真中在预定航迹上及飞行走廊内设置有4组大小一致的线塔。
4.2 仿真结果及分析
当飞行器在飞行过程中发现原航迹上出现了新的威胁后,利用基于虚拟导航点的威胁回避算法可快速生成回避航迹,并沿着新的航迹进行机动转弯飞行,成功实现对威胁的规避,同时能够准确回到初始航线上,仿真结果如图8和图9所示。
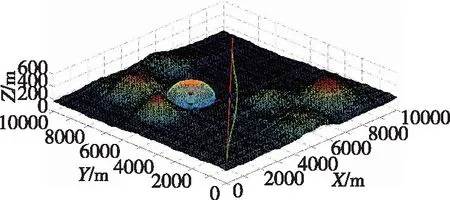
图8 直飞过程威胁回避三维航迹Fig.8 3D trajectory of threat avoidance on straight-flight process
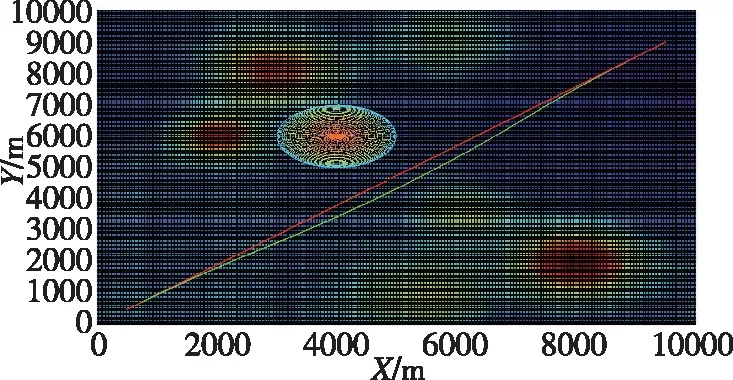
图9 直飞过程威胁回避二维航迹Fig.9 2D trajectory of threat avoidance on straight-flight process
当飞行器在机动规避的过程中再次探测到前方回归航迹上存在新的威胁(此时当前飞行航向与回归航向不一致),采用相应的算法快速计算出可行的虚拟导航点,生成另一条重规划航迹,实现了在机动规避过程中的威胁回避,同时回归到预定设计的航迹上,仿真结果如图10和图11所示。
图12所示为利用飞行器的纵向机动能力预测的纵向飞行航迹,用于回避代价的计算。

图10 机动过程重新发现威胁后的三维回避航迹Fig.10 3D trajectory of threat avoidance on maneuvering process

图11 机动过程重新发现威胁后的二维回避航迹Fig.11 2D trajectory of threat avoidance on maneuvering process

图12 纵向预测航迹仿真结果Fig.12 Simulation result of vertical predict trajectory
以上仿真结果表明,该算法计算量小,计算速度快,对计算机内存和处理速度的要求不高,能够适用于亚声速无人飞行器在线进行威胁回避的使用需求。
5 结论
对突发威胁或障碍快速做出反应是飞行器实现智能自主飞行的关键[11]。本文从飞行器在突发威胁下进行自主回避的实际需求出发,采用基于虚拟导航点的威胁回避算法,对飞行器自主威胁回避问题进行了初步研究,取得了比较满意的结果。
该算法具有普遍的适用性,还可以用于基于视觉的飞行器智能避障或局部在线航迹重规划等技术研究中。本文提出的算法原理简单,相比于全局寻优算法计算量小,易于工程实现,对于实现飞行器自主、智能化具有重要意义。由于该算法是以牺牲全局最优为代价来获取快速计算结果的,因此后续还需要针对不同类型的仿真环境进一步验证算法的适应性和有效性。
