旋转加速度计式重力梯度仪动态测量适应性能试验与效果分析

杨 晔，李 达，李城锁，高 巍

(天津航海仪器研究所，天津 300131)

0 引言

重力梯度仪是用于测量重力场梯度分布的精密设备，基于Bell Aerospace公司提出的旋转加速度计测量原理的重力梯度仪(后文中简称梯度仪)是迄今唯一实用的近地表动态测量重力梯度仪[1-3]。在飞机等运动平台上实现重力梯度测量，需采取减振和稳定平台等一系列工程化方法，降低载体的动力学干扰[4-6]。本文结合科研试验和实测数据来验证工程化方法的有效性，为实现动态条件下重力梯度的有效测量奠定基础。

1 动态测量误差机理

如图1所示，旋转加速度计式重力梯度仪基于加速度计位置差分测量原理，通过机械旋转的方式将重力梯度张量分量调制到系统旋转频率的二倍频处，加速度计输出与重力梯度张量分量之间的关系可表示为[7-8]：

(a1+a3)-(a2+a4)=2R(Γxx-Γyy)sin2ωt+

4RΓxycos2ωt

(1)

式中，a1、a2、a3、a4是4个加速度计的输出，R是加速度计检测质心到旋转中心的距离，Γxx、Γyy、Γxy是重力梯度张量分量，ω是旋转装置的旋转角速度。

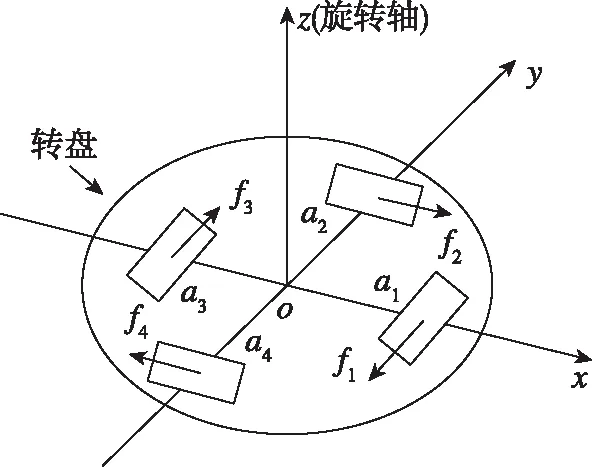
图1 旋转加速度计式重力梯度仪测量原理Fig.1 Measuring principle of gravity gradiometer with rotating accelerometer

1.1 载体线运动误差机理

在动态条件下，载体水平线运动对加速度计组合输出信号引起的牵连平动力干扰机理如下：

Aout(a0x,a0y)= [(K4-K2)a0y+(K1-K3)a0x]sinωt+

[(K4-K2)a0x-(K1-K3)a0y]cosωt

(2)

式中，Ki(i=1,2,3,4)是第i个加速度计的标度因数，a0x、a0y是载体东向、北向的线加速度。

Aout(a0z)=a0z[(Δβ1+Δβ3)-(Δβ2+Δβ4)]

(3)

式中，βi(i=1,2,3,4)是第i个加速度计敏感轴的垂向角度安装误差，a0z是载体的垂向加速度。

从式(2)、式(3)可以看出，线运动低频处分量与梯度仪对称安装的加速度计标度因数不一致误差或敏感轴俯仰角误差相耦合，汇入重力梯度信号形成测量误差。

1.2 载体角运动误差机理

在动态条件下，载体角运动对加速度计组合输出信号带来的牵连切向力与向心力干扰机理如下[12]：

2ΩxΩyRcos2ωt

(4)

式中，Ωx、Ωy是敏感器的东向、北向角速度。

(5)

2 动态测量工况分析与抑制方法

2.1 振动谱分析

以国内航空遥感作业常用的Y-12固定翼飞机的实际飞行参数为例，其典型工况下载体的三方向线加速度如图2所示，对其进行功率谱分析，得到机载条件振动谱，如图3所示。

图2 机载条件载体的东向线加速度(上)、北向线加速度(中)和天向线加速度(下)Fig.2 East acceleration (top), north acceleration (middle) and vertical acceleration (bottom) of the airborne conditional carriers

图3 机载条件载体的东向线加速度(上)、北向线加速度(中)和天向线加速度(下)功率谱密度Fig.3 Power spectral density of east acceleration (top), north acceleration (middle) and vertical acceleration(bottom) of the airborne conditional carriers

从图2可知，机载条件下垂向振动幅度比水平振动幅度大1倍左右，且在垂向振动传递过程中直接与加速度计敏感轴垂向安装误差相耦合，需重点抑制。

2.2 摇摆谱分析

在固定翼飞机平稳飞行过程中，不仅存在3个方向的线运动，还存在三自由度的角运动，其角速度如图4所示，对其进行功率谱分析，得到机载条件摇摆谱，如图5所示。

图4 机载条件载体的东向角速度(上)、北向角速度(中)和天角速度(下)Fig.4 East angular velocity (top), north angular velocity (middle) and vertical angular velocity (bottom) of the airborne conditional carriers

图5 机载条件载体的东向角速度(上)、北向角速度(中)和天向角速度(下)功率谱密度Fig.5 Power spectral density of east angular velocity (top), north angular velocity (middle) and vertical angular velocity(bottom) of the airborne conditional carriers.

从摇摆谱可知，机载条件下在16.8Hz和29Hz附近存在2个谐波频率，这对稳定平台的设计提出了严苛的要求。

2.3 动态测量技术关键

利用减震装置和稳定平台等一系列物理措施降低载体运动对重力梯度测量的影响，是实现重力梯度动态测量的关键措施之一[10-11]。

虽然在系统设计中采取加速度计标度一致性调整环节来抑制载体水平运动扰动的影响。但是还需要通过对机载运动环节以及测量原理中旋转调制特性和敏感元件性能进行分析，设计专门的气弹簧辅助海绵减震材料的宽频可变刚度复合减震装置，以适应不同工况条件对重力梯度测量的影响。在保证敏感元件在载波频率附近幅频响应高精度的同时，大幅抑制载体机动过程中加速度计非线性环节带来的不确定影响[14-17]。

采用稳定平台是抵御角运动干扰的主要措施。由式(4)、式(5)可知，经稳定平台隔离的残余角运动高阶项进入重力梯度信号，因此，动态重力梯度测量需对惯性稳定平台的角速度隔离刚度和带宽性能提出严格要求，保证对载体角运动的衰减程度[13,18]。

具体设计工作不在此赘述，本文仅提供对试验过程和效果的描述。

3 动态适应性试验

针对重力梯度飞行测量，开展梯度仪地面模拟动态适应性试验，考核模拟机载条件下梯度仪输出信号特性，为系统航空试验和后续改进提供试验依据。

3.1 振动试验实施与效果分析

3.1.1 垂向振动试验

梯度仪垂向振动试验如图6所示，输入的垂向线振动激励功率谱密度为图3所示天向线振动谱高频部分(5Hz以上)，解调后重力梯度信号如图7所示。

图6 重力梯度仪垂向振动试验现场图Fig.6 Field diagram of vertical vibration test for gravity gradiometer

图7 重力梯度信号垂向振动/静止状态对比图(Γxx-Γyy)Fig.7 Comparison of vertical vibration and static state of gravity gradient signals (Γxx-Γyy)

如图7所示，在高性能减震装置的作用下，梯度仪可以在机载垂向振动条件下获得稳定的重力梯度信号，系统输出在静态/垂向振动状态间没有明显的变化，与静态下信号噪声大致相当，且信号均值变化小于20E。

3.1.2 水平振动试验

梯度仪水平振动试验如图8所示，输入的水平线振动激励功率谱密度为图3所示水平线振动谱高频部分(5Hz以上)，系统输出重力梯度信号Γxx-Γyy如图9所示，重力梯度信号Γxy如图10所示。

图8 重力梯度仪水平振动试验现场图Fig.8 Field diagram of horizontal vibration test for gravity gradiometer

图9 重力梯度信号水平振动/静止状态对比图(Γxx-Γyy)Fig.9 Comparison of horizontal vibration and static state of gravity gradient signals(Γxx-Γyy)

图10 重力梯度信号水平振动/静止状态对比图(Γxy)Fig.10 Comparison of horizontal vibration and static state of gravity gradient signals (Γxy)

如图9、图10所示，在高性能减震装置的作用下，梯度仪可以在机载水平振动条件下正常工作。但由于动态条件下对表标度因数一致性调整环节也形成干扰，载体水平运动低频分量与其不一致误差相耦合，汇入重力梯度信号(尤其是Γxy信号)造成重力梯度信号低频噪声较静态增加了35%(0.01～0.1Hz)。

3.2 摇摆试验实施与效果分析

3.2.1 水平摇摆试验

如图11～图13所示，水平摇摆试验中典型解调输出的梯度信号如图12、图13所示(摇摆角度为2°，摇摆周期为20s)，从中可以看出，在654s系统由静态开始摇摆时，梯度信号Γxx-Γyy出现64.5E的阶跃现象，梯度信号Γxy出现-40.8E的阶跃现象。与水平线振动输出信号噪声增大原因相同，水平摇摆产生的低频线运动与加速度计标度因数不一致误差相耦合，造成重力梯度信号产生阶跃。

图11 梯度仪水平摇摆试验现场图Fig.11 Field diagram of horizontal swing test for gravity gradiometer

图12 重力梯度信号水平摇摆/静止状态对比图(Γxx-Γyy)Fig.12 Comparison of horizontal swing and static state of gravity gradient signals (Γxx-Γyy)

图13 重力梯度信号水平摇摆/静止状态对比图(Γxy)Fig.13 Comparison of horizontal swing and static state of gravity gradient signals (Γxy)

3.2.2 方位摇摆试验

梯度仪方位摇摆试验重力梯度信号如图14、图15所示(摇摆角度为5°，摇摆周期为10s)。结果表明，梯度仪可通过稳定平台有效隔离载体方位角运动，摇摆状态下输出的两路重力梯度信号噪声水平与静态下信号噪声相当。

图14 重力梯度信号方位摇摆/静止状态对比图(Γxx-Γyy)Fig.14 Comparison of azimuth swing and static state of gravity gradient signals (Γxx-Γyy)

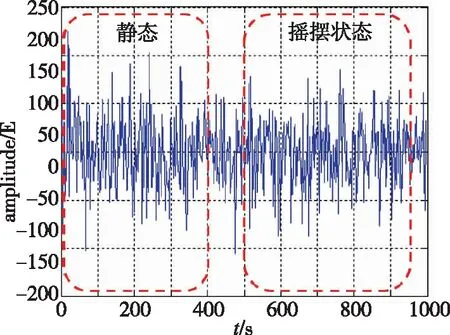
图15 重力梯度信号方位摇摆/静止状态对比图(Γxy)Fig.15 Comparison of azimuth swing and static state of gravity gradient signals(Γxy)

4 试验总结与展望

上述实验初步验证了重力梯度仪在模拟机载条件下可正常反映敏感器噪声水平，但在水平线运动激励下，重力梯度信号输出较静态下输出信号噪声增大了35%。因此，需提高对表标度因数一致性动态调整控制性能以抑制水平运动对重力梯度测量的影响。此外，以上试验的数据均在地面模拟条件下获得，与航空试验的高动态环境仍存在差距。后续计划开展车载与航空试验，进一步验证梯度仪缓冲、减震装置的有效性，提高系统的动态测量能力，这将面临更加复杂和困难的技术挑战。