基于最小约束系统的分布式协作定位研究
2019-03-13章平,王炎,王桥
章 平,王 炎,王 桥
(1.安徽工程大学计算机与信息学院,芜湖 241000;2.东南大学信息工程学院,南京 210096)
0 引言
手机定位技术伴随着移动通信的发展不断进步。早在20世纪80年代,1G蜂窝移动通信可以根据基站位置和接收信号强度而粗略估计出接收机的位置信息,进而提升通信系统性能或者提供相关应用[1-5]。进入90年代,随着2G和3G数字通信技术发展,各种定位技术相继出现,如Cell-ID、TA、OTD、uplink ToA、 enhanced OTD (E-OTD) 以及A-GPS等。1999年,美国联邦通信委员会(Federal Communications Commission, FCC)在紧急服务E911中对手机定位提出要求:移动端定位要以67%的概率定位在50m以内,95%的概率定位在150m以内;网络端定位要以67%的概率定位在100m以内,95%的概率定位在300m以内[6]。
2000年5月,美国克林顿政府下令停止执行全球定位系统(Global Positioning System,GPS)中选择性可用性(Selective Availability,SA)干扰策略,全球的民用GPS接收机的定位精度一夜之间提高了10倍,在室外达到了10m以下的定位精度,初步解决了手机的室外定位问题。此后,随着基于位置服务的兴起,对手机定位的精度以及覆盖范围都提出了更高的要求。美国FCC甚至要求手机运营商在2020年将手机定位的精度提升到m级。进入5G时代,各种新兴的通信技术和手机应用都需更高精度的定位服务,如信道分配、波束成形和生活协助等,对传统手机定位技术提出了巨大的挑战[7]。
在4.5G的研究中,已有相关研究通过已经定位的设备和位置未知设备之间的设备到设备(Device-to-Device,D2D)间通信的测量进行协作定位[9]。协作定位是一种利用位置未知节点间的测量信息获取节点间的相对位置信息的定位方式,在无线传感器网络定位中有着重要的作用,不但可以提升定位精度,更拓展了传统定位的可定位范围[8]。
5G条件下,D2D通信作为一种低功耗、自适应和高效率的通信方式,将会得到重要应用。该通信方式将产生大量的设备之间的信号测量,可被用于估计设备之间的距离甚至角度信息,将被用于实现高精度(m级以下)、低时延、大容量和全覆盖的定位。同时,固定部署的基站或者热点,现有移动定位技术也提供了各种精度不一的位置信息。如何利用设备之间的信号测量提升位置精度成为迫切需要解决的问题[10]。
本文提出了一种基于最小约束系统的分布式协作定位方法。该方法利用节点的现有位置构造最小约束系统[13],用来确定网络中心的位置和网络的朝向。然后通过极大化由节点间测量决定的似然函数,优化节点间的相对位置。理论上,当用节点的真实位置构造最小约束系统后,可以完全准确给出网络的位置和朝向,剩下的定位误差都是由节点间测量误差造成的。
该定位方法还具有分布式和可扩展的特点。事实上,任意选择部分节点位置构造最小约束系统,均可通过节点间的测量更新节点间的相对位置,进而通过迭代实现网络所有节点位置的更新。考虑到极大似然估计要求解非线性最小二乘问题,分布式的实现有助于降低算法复杂度以及节点间的通信次数。
本文安排如下:第1节介绍了定位的场景及节点间距离测量模型;第2节引入了最小约束系统,并讨论了如何构造最优的最小约束系统;第3节详细介绍了基于最小约束系统的协作定位及其分布式实现;第4节进行了仿真验证;第5节总结全文。
1 定位场景及数学模型
5G移动通信系统中,除了移动终端与基站之间通信外,移动终端之间的D2D通信也产生了大量的节点间信号测量。这些测量包括信号强度、到达时间甚至到达角度等,提供了节点(包括移动终端和基站)之间的相对位置信息。为了方便起见,这里假定从信号测量中获得距离信息,建模如下:
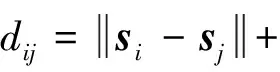
(1)
通过模型式(1),可以得到在距离测量下,节点位置向量s=[s1,s2,…,sn]T的对数似然函数:
(2)
其中,Ε为所有距离测量的下标集,c为与位置向量s无关的常数。
极大化对数似然函数式(2)可得节点位置的估计。但是,由于节点间的距离测量无法提供网络的位置和朝向信息,因此该估计并不唯一。为了唯一定位,通常引入锚节点,即位置已知的节点,提供外部约束信息。
在5G移动通信系统中,基站以及各种无线网络接入点如WiFi和蓝牙热点等位置相对固定,可以担任锚节点的角色。具体地,令Α为锚节点下标集合,有:
sk=ak,k∈Α
(3)
其中,ak=[akx,aky]T已知锚节点坐标。
理论上,在约束式(3)下,极大对数似然式(2)得到的估计具有渐进最优性。但在实际应用中却存在如下问题:
1)无法保证锚节点位置的准确性。无论基站还是各类热点,其位置精度受各自定位方法限制,精度各异,甚至会由于位置移动,提供错误的锚节点位置信息。在等式约束式(3)下,锚节点的位置误差不仅影响网络整体的位置和朝向的估计,更会错误地约束节点间相对位置信息,影响相对位置估计精度。
2)约束式(3)下极大对数似然式(2)是一中心化算法,需要所有节点间测量及锚节点位置信息,在大规模网络中通信及计算代价较高。
3)算法扩展性有限。新增移动终端及相应的节点间测量后,需要重新进行全局优化,无法局部更新。
2 最小约束系统及其最优性
在节点间测量可以提供足够相对位置信息的情况下,只需要将其中1个节点定在坐标原点,另外1个节点定在x轴上,第3个节点的纵坐标的符号为正即可唯一确定其他节点。换言之,3个连续的约束即可实现唯一定位(最多相差一个整体发射变换),称之为最小约束系统(Minially Constrained System, MCS)[11]。 问题是,如何构造一组最优的约束使得定位误差最低。
文献[14]提供了一种利用参考位置构建最小约束系统的方法,并证明了当参考位置恰好是真实位置时,该最小约束系统是最优的。具体地,令r=[r1x,r1y,r2x,r2y,…rnx,rny]T为一个参考位置向量,定义如下线性约束:
(4)
(5)
(6)
其中,式(4)和式(5)分别利用参考位置确定了网络中心的位置,而式(6)指明了网络朝向。特别地,这3个线性约束在(定位之前)令r=s时,网络中心和朝向完全正确,可以提供最优的定位精度。实际应用中,一般选择节点的初始位置(通过GPS或者其他定位算法获得)即可。
几何上,线性约束等价于将位置向量s对应的相对构型通过Partial Procrustes Fit[13]拟合到参考位置向量r上,即:
(7)
式(7)是满足式(4)、式(5)和式(6)的一组解。其中,T(s)代表网络整体平移和旋转变换,即刚性变换,Γ=diag(Γ0,Γ0,…,Γ0)是由n个2×2正交阵构成的2n×2n维块对角矩阵,代表节点整体的旋转(包括反射),1x=[1,0,1,0,…,1,0]T和1y=[0,1,0,1,…,0,1]T分别为2n维向量,与实数x和y构成了x轴方向和y轴方向的平移变换。
本文将以节点已有位置作为参考位置向量,利用节点间的距离约束更新已有位置中的相对位置部分,保留网络整体位置和朝向不变。
3 算法流程
3.1 参考位置估计
移动通信系统中,基站或者接入点一般都会通过GPS或者人工部署的方式获得位置信息;手机也可以通过GPS模块在室外定位,并通过惯性导航或者室内热点实现室内位置的更新。这些都可以作为节点参考位置估计。特别地,对于没有参考位置估计的节点,建议采用DV-Hop或者DV-Distance算法获得位置估计,具体过程参见图 1。

图1 参考位置估计算法流程Fig.1 Reference location estimation algorithm flow
3.2 约束极大似然估计
基于最小约束系统的分布协作定位算法的核心是基于参考位置构造最小约束系统,然后在约束下求解极大似然估计,大致流程参见图 2。

图2 约束极大似然估计流程Fig.2 Constrained maximum likelihood estimation flow
在线性约束式(4)、式(5)和式(6)下,极大化对数似然式(2)可以通过两种方法实现:
1)求解线性约束的基础解系,将约束极大似然重参数化为无约束的极大似然函数,然后使用求解非线性最小二次问题的数学工具迭代求解。
2)直接极大化对数似然式(2),尽管迭代结果不唯一,但是将最终结果利用Partial Procrustes Fit拟合到参考位置向量上,则获得一组极大化式(2),又满足线性约束式(4)、式(5)和式(6)的位置估计。
3.3 算法的扩展与分布式实现
由于任意给定参考位置集合,都可以构造最小约束系统,并对该集合的节点位置进行更新。因此,该定位算法具有很好的扩展性,并可以进行分布式实现。
假设引入新的节点,其参考位置可以通过相邻(已定位)节点使用DV-Hop或者DV-Distance进行定位。该参考位置可以与相邻节点的参考位置一起构造最小约束系统,并在该约束系统下,通过节点间测量对应极大似然估计更新该节点及相邻节点的位置。
此外,网络也可被划分成若干部分,在每一个部分构造最小约束系统,通过约束极大似然估计进行分布式定位。注意,仅仅分块定位的话,分块之间的测量并没有用到定位过程中,因此建议通过迭代的手段,将所有节点间的测量引入定位过程,具体参见图 3。该方法仅仅是一种最简单的选择,更多优化策略留待后继研究。
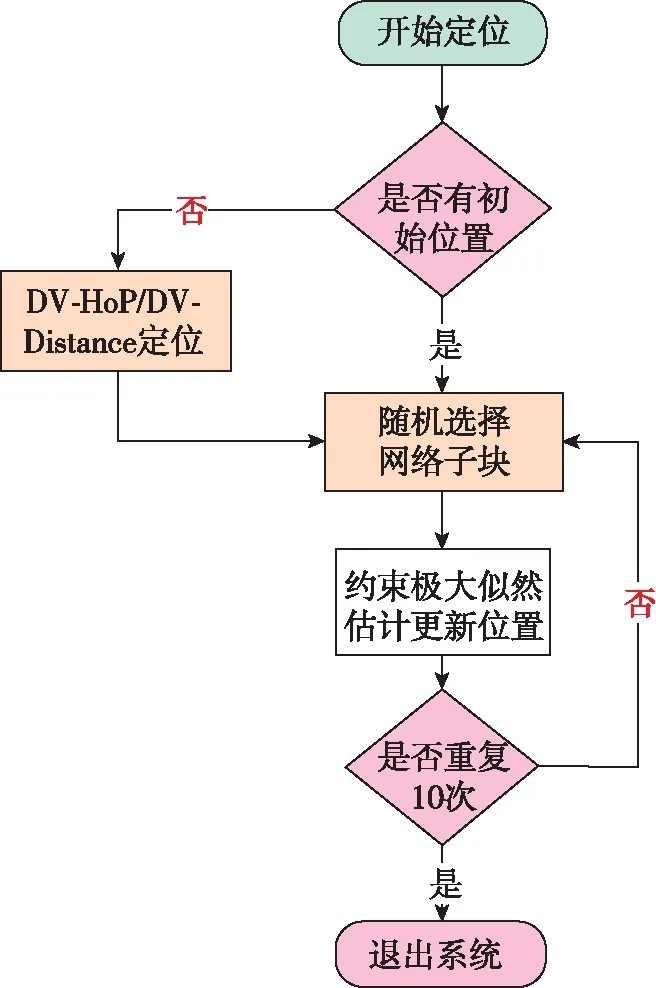
图3 分布式协作定位流程Fig.3 Distributed cooperative localization flow
4 仿真分析
为了验证算法性能,首先利用节点真实位置构造最优最小约束系统,研究算法在不同测量误差下的定位性能;然后,利用DV-Distance算法获得节点初始位置,从而构造最小约束系统,并研究在该约束系统下的定位性能;最后,通过随机分组的方法,研究了算法的分布式实现及其性能。不失一般性,距离单位为m,相应的均方误差单位为m2。
在10×10的平面上进行仿真。平面上随机生成50个节点,设置通信半径为3,得到一个部分连通的网络,参见图4。节点间的距离测量由模型式(1)生成,噪声方差的变化范围为从-30dB~10dB。
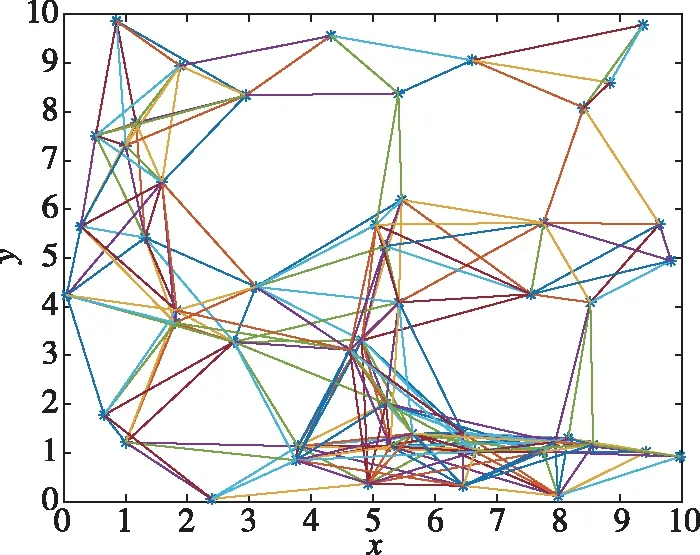
图4 二维部分连通网络Fig.4 Two-dimensional partial connected network
4.1 真实位置作为参考位置
将参考位置设置为节点真实位置下,可以得到最优的定位精度。如图 5所示,定位精度完全由节点间测距精度决定,当测距误差趋向于0时,定位误差也趋向于0。

图5 利用真实位置构造约束系统算法性能Fig.5 Algorithm performance of constrained system constructed by real locations
4.2 基于锚节点估计参考位置
实际中,由于无法得到节点的真实位置,通过将4个节点设置为位置已知的锚节点,引入DV-Distance算法获得其他节点的初始位置,并进而构造出一个最小约束系统。
图 6给出了在该约束系统下的定位性能。从图6中可以看出,相比初始位置,利用约束极大似然估计获得的定位精度明显提升。

图6 利用估计位置构造约束的算法性能Fig.6 Algorithm performance of constrained system constructed by estimated locations
4.3 分布式实现
考虑到约束极大似然本质上是一个中心化的非线性最小二乘问题,需要较高的通信量汇集测量值并实施高维参数迭代优化。提出的分布式实现则是一个降低通信和算法复杂度的有效策略。具体地,在每次实验中随机选择10个节点,基于10个节点的初始位置和节点之间的测量实施该算法,更新节点位置。为了尽可能使用节点间的测量,随机选择10次,迭代更新,最终的结果作为定位结果。图 7展示了定位性能,相对于集中式算法,分布式迭代算法的定位精度有所下降,但仍然提升了参考位置的精度。

图7 分布式协作定位性能Fig.7 Distributed collaboration location performance
5 结论
5G移动通信系统中,采用D2D的通信方式为协作定位技术的引入提供了技术保证。考虑到现有的GPS、蜂窝定位以及无线局域网定位(如WiFi定位和蓝牙定位)等定位技术提供了精度各异的定位结果,本文提出了基于最小约束系统的分布式协作定位方法,该方法:
1)利用D2D测量确定节点间的相对位置信息,而将网络整体的位置和朝向留给已知参考位置确定;
2)可用GPS、DV-Hop和DV-Distance等多种算法获得参考位置信息,且无需知道参考位置的精度;
3)具有分布式和可扩展特性,可以为5G网络中大量终端提供位置信息。
