一种圆锥运动条件下的等效旋转矢量算法研究

王文举，刘生攀

(贵州航天控制技术有限公司，贵阳 550009 )

0 引言

在捷联惯导系统的姿态、速度和位置更新算法中，姿态算法对整个系统精度的影响最大，它是算法研究和设计的核心。姿态算法有欧拉角法、方向余弦法、四元数法、旋转矢量法等[1-2]。欧拉角算法包含三角运算，实时计算有一定的困难，且在一定条件下方程出现退化，不适用全姿态的解算。方向余弦法避免了欧拉角法中的方程退化问题，但计算量大，工程中并不实用。四元数法计算量小，实现简单，工程中较实用，其本质是旋转矢量法中的单子样算法，没有对有限转动过程中的不可交换误差进行补偿，比较适合低动态载体的姿态解算，对于高动态载体，算法漂移会比较严重。旋转矢量法采用多子样算法对不可交换误差进行补偿，算法实现简单，并且可以对系数进行优化，适用于角运动频繁或角振动的载体姿态解算。

为了解决角运动过程中的不可交换误差，1971年Bortz提出了旋转矢量法，它有2个计算步骤，先求解旋转矢量，再进行四元数更新。目前的旋转矢量多以角增量为参数进行求解，根据姿态更新周期内对陀螺输出角增量等间隔采样数的不同，等效旋转矢量的求解可分为单子样法、双子样法、三子样法和四子样法等[3-9]。

对于给定的捷联姿态算法，需要采用一定的测试输入来评价其性能。对于捷联惯导姿态更新，经典圆锥运动是最恶劣的工作环境条件之一，它会诱发数学平台的严重漂移，所以对旋转矢量算法作优化处理。通常采用经典圆锥运动作为环境条件，如果能确保圆锥运动环境条件下算法精度高，就能确保在其余环境条件下算法精度高[10-11]。

本文首先介绍了经典圆锥运动，常用的等效旋转矢量法，然后详细推导了一种新的等效旋转矢量法，并且以经典圆锥运动作为姿态算法的测试输入。仿真结果表明，姿态、速度、位置精度得到了明显提高。

1 经典的圆锥运动

经典圆锥运动下载体运动可以用旋转矢量表示为[12]：

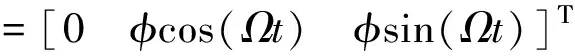
(1)

其中，φ是圆锥运动的锥半角，Ω是圆锥运动的角频率。任意t时刻，载体坐标系绕Oybzb平面上的转轴Φ相对于惯性坐标系转动φ角度，转轴时刻在变化而转角恒定不变，载体坐标系的xb轴在空间画出一个圆锥面(半锥角为φ，xb轴为锥轴)，如图1所示，这正是该角运动称为圆锥运动的原因。

经典圆锥运动时，载体相对惯性空间的角速率在载体坐标系的分量为：

(2)

经典圆锥运动对应的载体更新四元数为：

(3)

2 等效旋转矢量算法

等效旋转矢量法也是建立在刚体矢量旋转思想的基础上，与四元数法的不同在于：在姿态更新周期内，四元数法直接计算姿态四元数，而旋转矢量法先计算姿态变换四元数，再计算姿态四元数。旋转矢量的微分方程如下：

(4)

式中，旋转矢量的导数等于ω再加上2个修正项，而修正项反映了不可交换误差产生的影响。目前，旋转矢量算法多以角增量为参数，基于泰勒级数展开进行多子样求解，如单子样法、双子样法、三子样法、四子样法等。双子样算法公式如下：

(5)

三子样算法公式如下:

(6)

高阶泰勒级数展开原则上要求函数Φ足够光滑，而实际陀螺输出总会或多或少包含电气噪声，噪声并不反映载体的真实角运动，同时对角速度函数的光滑性也造成不良影响。因此，多子样算法的精度有限，并非子样数越多算法的实用精度就越高，并且高子样的计算量较大。在选择子样数时，应权衡利弊，兼顾精度要求、计算速度等方面。

3 一种新的等效旋转矢量算法

旋转矢量算法多以角增量为参数进行求解，激光陀螺一般输出为角增量，但是光纤陀螺输出为角速率[13]。如果把角速率转化为角增量，很难保证旋转矢量精度不受影响，这一差异使得使用角增量代替旋转矢量进行姿态更新时会产生误差，并且误差随时间会不断累积。本节在旋转矢量算法的基础上研究了一种新的等效旋转矢量算法，该算法使用角增量和角速率，以角速率为主，等效旋转矢量精度更高，与二子样算法相比较，圆锥误差补偿精度得到进一步提高。

类似于传统二子样算法的推导思路，陀螺在一个计算周期(T，T+h)内，需要3次陀螺采样值，假设h内输出可表示为：

ω(τ)=a+2bτ+3cτ20≤τ≤h

(7)

记角增量为：

(8)

可计算Δθ(0)及其各阶导数，如下：

(9)

由于姿态更新周期h一般为毫秒级，旋转矢量Φ也可视为小量[14]。

Φ(τ)≈Δθ(τ)

(10)

忽略高阶小量，式(4)可以写成：

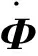
(11)

可计算Φ(0)的各阶导数，如下：

(12)

将Φ(h)用泰勒级数展开[15]，得：

(13)

(14)

将式(14)代入式(13), 其中：

可知：

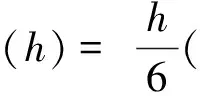
(15)

并考虑陀螺的角增量输出，则旋转矢量可用式(16)估计：

Φ=Δθ+Xh2ω1×ω3+Yh2ω2×(ω3-ω1)

(16)

式中：

在圆锥运动条件下，捷联惯导姿态更新过程会诱发数学平台的严重漂移。因此，以圆锥运动作为测试条件，对旋转矢量算法中的系数作优化，根据圆锥运动可得到理论四元数q(h)，利用旋转矢量

(17)

4 仿真分析

捷联惯导加表零偏稳定性在100μg，陀螺零漂稳定性在0.01(°)/h，惯性器件采样周期为5ms，姿态更新周期10ms。以经典圆锥运动作为姿态输入，锥半角为1°，角频率为8Hz，导航时间为1h。对比双子样法与新的等效旋转矢量法的解算效果，如图2～图7所示，在姿态精度、速度精度、位置精度等方面，新的算法都优于传统的二子样算法，并且计算量相当。

图2 航向角误差对比图Fig.2 Contrast diagram of heading error

图3 俯仰角误差对比图Fig.3 Contrast diagram of pitch error

图4 横滚角误差对比图Fig.4 Contrast diagram of roll error

图5 东向速度误差对比图Fig.5 Contrast diagram of east direction velocity error

图6 北向速度误差对比图Fig.6 Contrast diagram of north direction velocity error

图7 位置误差对比图Fig.7 Contrast diagram of position error

5 结论

本文根据光纤陀螺输出为角速率的特点，在旋转矢量姿态更新算法的基础上研究了一种新的圆锥误差补偿表达式。等效旋转矢量使用角增量和角速率，以角速率为主，其精度高于二子样算法，运算量相当，通过仿真验证了改进算法具有较高的精度，且计算量相对较小，易于工程实现，为光纤陀螺捷联系统姿态算法解算提供了一个更为有效的途径。