非线性总体最小二乘反演道路圆曲线参数算法

胡 川， 邓明镜， 赵立都

(重庆交通大学 土木工程学院，重庆 400074)

0 引 言

直线、缓和曲线和圆曲线是道路平面线形的基本元素。线形参数的反演，在公路普查、建立现有道路路线图形数据库等方面具有非常重要的作用，特别是圆曲线参数，影响着缓和曲线参数、道路里程的计算结果[1]。重心坐标法[2-3]、附有参数的条件平差法[4]和最小二乘法[5]是3种较为常见的圆曲线参数估计方法。重心坐标法是根据不在同一条直线上的3点确定一个圆，将所有观测坐标进行排列组合，计算各组合点的圆心坐标和半径，取所有组合计算结果的平均值作为圆曲线参数的估计值。该方法的优点是计算简单，缺点是平差理论不够严密；附有参数的条件平差是将圆曲线参数估计的非线性最小二乘模型转化为附有参数的条件平差模型，采用经典平差结果直接计算参数估计值。该方法的优点是平差理论相对严密，缺点是参数估计结果易受参数近似值(初值)的影响[6]。最小二乘法以观测点到圆曲线距离的平方和为极小值条件，采用换元法将其转化为普通最小二乘平差模型[7]。该方法的优点是避免计算非线性问题，缺点是其极小值条件不完全合理，且不具有明确的几何意义。道路圆曲线参数反演既要计算参数[8-9]，还要估计误差值，为剔除粗差影响提供基础保障[10]。近年来，非线性总体最小二乘(nonlinear total least squares，NTLS)引起了测绘数据处理领域的研究兴趣[11]，针对上述问题，笔者提出一种基于NTLS的道路圆曲线参数反演算法，直接用观测误差定义平差极小值条件(平差准则)，减小参数初值对估计结果的影响，以提高道路圆曲线参数反演精度和理论的严密性。

1 NTLS反演道路圆曲线参数模型

用离散观测数据反算道路线形参数，首先需要识别哪些点属于哪类线性，例如直线、圆曲线；其次是选用合理、可靠的数学方法估计其最佳参数值。笔者假设已识别出圆曲线上的观测数据，重点讨论估计圆曲线参数的NTLS方法。

假设现有GNSS接收机测量的m个圆曲线路面段离散坐标 (xi，yi)，i=1,2,…,m。设该圆曲线段的圆心坐标为(a，b)，半径为r，则估计该段圆曲线参数的函数模型可以表示为

[(xi-exi)-a]2+[(yi-eyi)-b]2=r2

(1)

式中：exi和eyi为与各坐标观测值相对应的随机误差。

NTLS的极小值条件是所有输入非线性系统的观测误差平方和最小。采用数学语言描述可表达为

(2)

式中：ex和ey分别为与向量x和y相对应的误差向量。用GNSS采集道路曲线坐标时，通常认为观测条件相同，属于等精度观测，观测误差服从期望为0，方差为σ2的正态分布，它们对应的权矩阵都是单位矩阵。

2 3种极小值条件的比较

附有参数的条件平差法、最小二乘法和NTLS，都是在某一极小值条件下，估计道路圆曲线参数的最佳近似值。它们的极小值条件分别为式(3)、式(4)和式(2)：

(3)

(4)

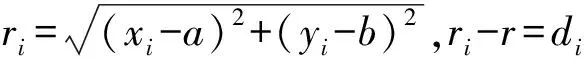
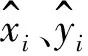
(5)

通过观察它们的几何关系，可以发现，观测误差exi、eyi和半径误差eri，分别是直角三角形的垂直边和斜边，它们满足勾股定理，即

(6)

(7)

比较式(7)和式(2)，不难发现它们具有一致性，这说明，同附有参数的条件平差法一样，NTLS的极小值条件具有明确的几何意义，比最小二乘法定义的极小值条件更合理。

3 NTLS反演道路圆曲线参数的解算

将式(1)变形，得到非线性总体最小二乘平差函数式(8)：

f(ex,ey,a,b,r)=[(x-ex)-a]2+[(y-ey)-b]2-r2

(8)

令a=a0+δa，b=b0+δb，r=r0+δr，对式(8)进行线性化，整理后可得

AE+Bξ-W=0

(9)

式中：

A=[A1,A2]

(10)

(11)

(12)

ξ=[δaδbδr]T

(13)

(14)

用上述符号，可将NTLS平差极小值条件式(2)重新表达为

ETPE=min

(15)

式中：P=I2m，I2m是大小为2m×2m的单位矩阵。

采用拉格朗日乘数法求解NTLS，首先需要构造目标函数，根据式(9)和式(15)，可将该目标函数描述为

F(E,ξ,λ)=ETPE+2λT(AE+Bξ-W)

(16)

式中：λ是拉格朗日乘子。

将式(16)分别对E，ξ和λ求偏导数，并令它们等于0，即

(17)

(18)

(19)

式中：带波浪线和小帽的符号分别表示最佳预测值和最佳估计值。

对式(17)～式(19)进行整理，可以得到参数修正值和误差预测值的计算公式，即

(20)

(21)

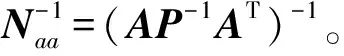
验后单位权方差的计算公式为

(22)

4 NTLS反演圆曲线参数算法

Step1：计算参数初值。

Step2：计算参数估计值。

1)计算观测量和半径的估计值

3)计算参数修正值和误差预测值

4)更新参数值

Step3：判断是否终止迭代。

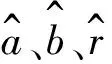
5 实验分析

为验证、测试笔者提出的算法，设计模拟数据(实验1)和实测数据(实验2)两个实验。

5.1 实验1

为保证模拟数据尽可能地接近实测数据，按如下规则产生1 000组含有随机误差的观测数据。首先，设置接近实际的圆心坐标和半径，(a,b)=(436000,32400)，r=700 ，单位m；其次，从180°开始，在圆心角为5°所对应的圆弧上，用参数方程，等间距计算出20个不含有误差的圆曲线点坐标；最后，给这些精确的坐标值，附加上期望为0，中误差为0.05 m(方差： 0.002 5 m2)的随机误差，模拟1 000次，得到1 000组模拟观测数据。

分别采用重心坐标法、最小二乘法、附有参数的条件平差法和NTLS对这1 000组数据进行拟合，估计出圆心坐标和半径，将4种方法每次估计的参数与真值做差，结果如图1。从图1可以看出：①4种方法的估计结果存在明显差异；②相对于其它两种方法而言，附有参数的条件平差法和NTLS的估计结果更稳定，特别是后者；③NTLS的估计值与真值最为接近；④附有参数的条件平差法估计的圆半径始终存在明显偏差。

图1 估计值与真值之差Fig. 1 Difference between estimated value and truth value

图2描述了附有参数的条件平差法和NTLS估计的验后单位权方差值，它们的平均值分别为24.379 7和0.002 7，显然，后者更接近先验值。

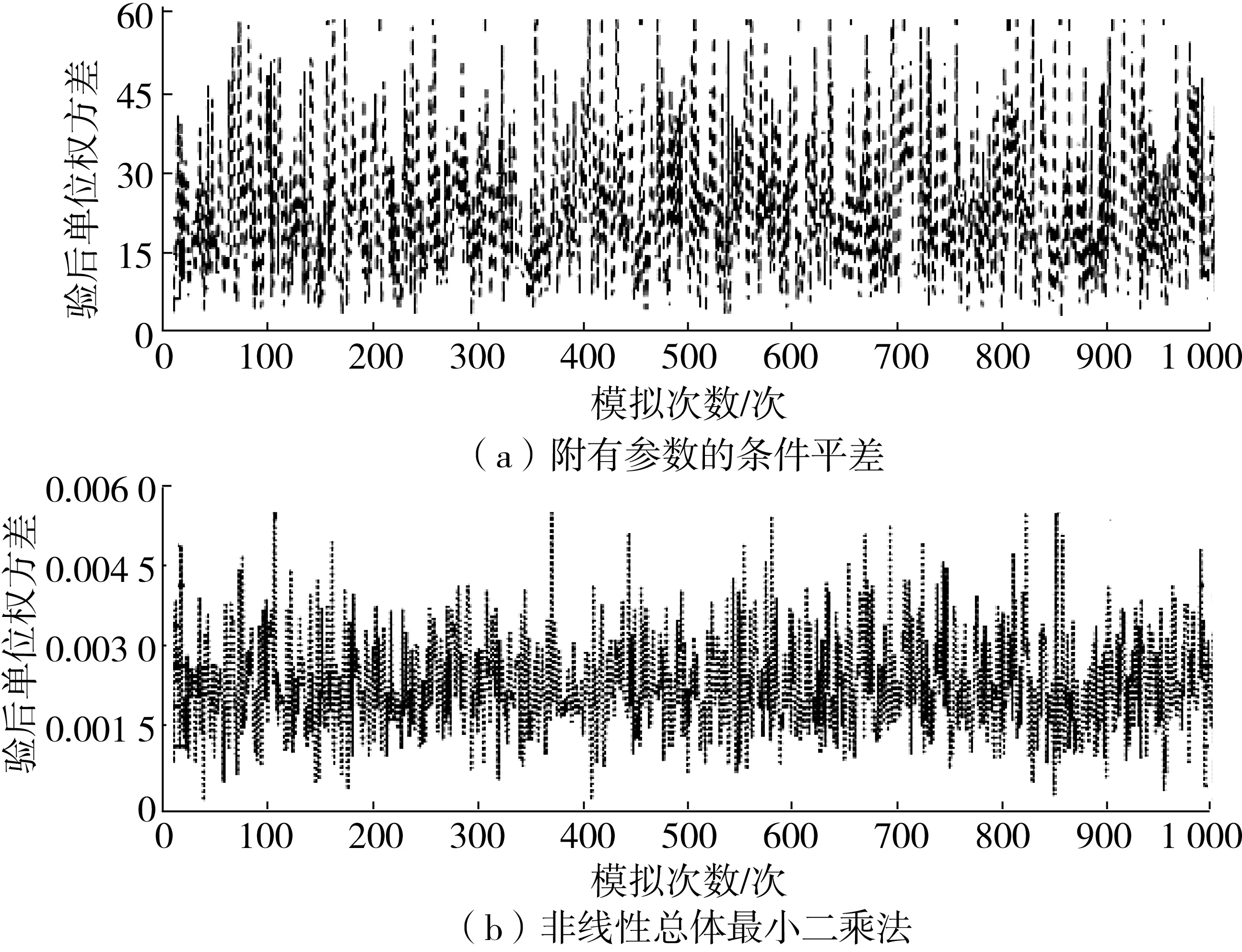
图2 验后单位权方差估计值Fig. 2 Estimated values of posteriori unit weight variance

5.2 实验2

实测数据实验，数据来源于文献[3]，如表1。仍然采用上述4种方法反演道路圆曲线参数，反演结果如表2, 对应的图形描述如图3。

表1 GNSS实测道路圆曲线坐标Table 1 GNSS measured road circular curve coordinates m

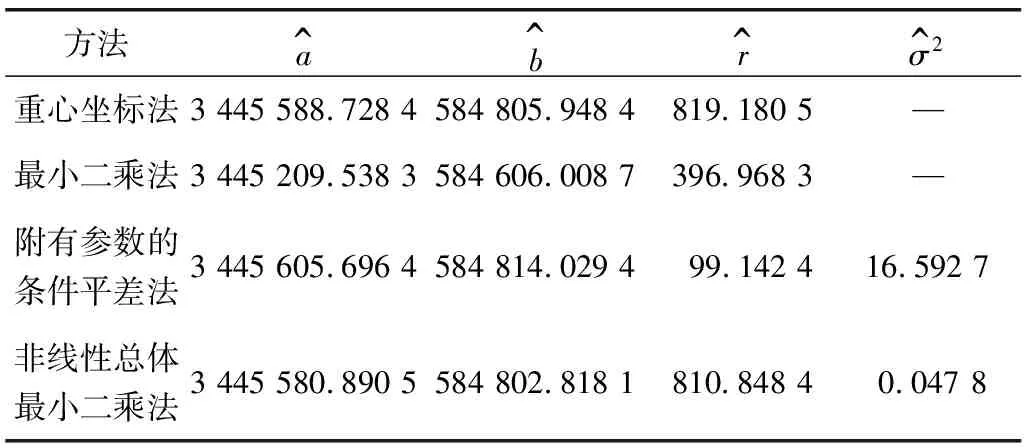
表2 实验2参数估计结果Table 2 Parameter estimation results in experiment 2 m

图3 实测道路圆曲线反演结果Fig. 3 Inversion results of measured road circular curve

从表2可以发现，4种方法的反演结果存在明显差异，其中附有参数的条件平差法反演的圆曲线半径明显小于其余方法，其验后单位权方差远大于NTLS，这与模拟计算结果一致。考虑到道路圆曲线的半径一般较大，在实验2中采用重心坐标法和NTLS更为合理。但是，考虑到实验1的结果，后者比前者不仅稳定性更好，而且更接近真值。因此，综合考虑，在道路圆曲线参数反演中推荐使用NTLS。

6 结 论

道路圆曲线参数的反演是恢复道路线形参数的关键。当采样点坐标x和y都含有误差时，同时考虑它们的影响，并直接对它们进行处理，有助于提高参数估计精度，增加平差理论的严密性。根据前文的讨论，在道路圆曲线参数反演中，可以得出如下结论：

1)NTLS的极小值条件等价于点到圆曲线距离平方和最小条件。

2)NTLS反演道路圆曲线参数，与其余3种方法相比较，不仅稳定性好，而且精度更高。

3)综合考虑，就笔者讨论的4种方法而言，推荐使用NTLS反演道路圆曲线参数。

事实上，不仅观测数据本身含有粗差，而且一些被错误识别的点也属于粗差，因此采用稳健总体最小二乘估计圆曲线参数其理论更严密，这将是我们进一步研究的方向。