被动吸振器组在传动系统宽频减振中的应用研究∗

高 普，项昌乐，2，刘 辉，2，周 晗

(1.北京理工大学机械与车辆学院，北京 100081； 2.北京理工大学，车辆传动国家重点实验室，北京 100081)

前言

车辆动力传动系统是车辆主要动力来源，通常情况主要由发动机、离合器和手动变速器或者液力变矩器和自动变速器、驱动轴、差速器、车轮等部件构成。动力传动系统的振动是车辆振动的主要来源之一，该系统部件众多，会产生多阶固有振动，是一个宽频振动系统[1-3]。由于气缸燃气压力和曲轴的往复部件惯性力，使得发动机的转矩波动为周期变化的信号，且为多频激励信号[4-5]。发动机的转速变化范围巨大，动力传动系统具有多阶固有振动频率，因此共振发生是很难避免的。一般情况下，发动机的怠速转速为 700-1 000r/min，工作转速为5 000-6 500r/min，大范围转速的变化使得波动转矩激励信号会穿越1阶或多阶动力传动系统的固有频率，导致系统在很宽的频率带均有可能发生共振。在车辆运转工况发生变化时，例如车辆快速加减速、快速通过减速带及高速重载工况，动力传动系统的共振更为明显，车辆整体的NVH性能恶化。

安装动力吸振器可有效改善机械系统的振动特性，依据动力吸振器是否需要外界动力源参与控制，可分为被动式动力吸振器、主动式动力吸振器和半主动式动力吸振器(自调谐动力吸振器)。其中被动吸振器，结构简单、易于安装，制造成本低，在工程中得到广泛应用[6-7]。吸振器固有频率与外界激励频率一致时，吸振器产生共振，起到减小主系统振动效果。被动吸振器的各个性能参数在设计初期确定之后不会再改变，这种固定的性能参数导致被动吸振器的工作频带极小，很难实现宽频减振。为了拓宽减振频带，将阻尼元件引入动力吸振器，对吸振器进行最优参数匹配是十分必要的[8-9]。周乾[10]指出优秀的被动吸振器参数优化设计能够有效提高减振效果，因此为了获得最优的减振性能参数，各种参数优化方案被提出，并且从单自由度吸振器减振系统扩展到多自由度系统，以拓宽减振应用的频率范围。本文即利用上述参数优化设计方法对传动系统被动扭转动力吸振器进行最优参数匹配。

在以往的减振器优化设计与控制策略研究中，只对某一部件或者某一特定的非常狭窄的振动频段，对于减小动力传动系统的整体宽频振动效果不明显。因此对宽频振动进行阶段性切割，在传动系统安装动力吸振器组，并在相应频段的相应关键位置安装对应结构简单的动力吸振器，分段控制振动，可有效解决传动系统振动频率宽的技术难题。

本文中针对车辆动力传动系统建立多自由度动力学模型，对系统特征值灵敏度分析，探究影响动力传动系统各阶固有振动的关键转动惯量，确定各共振频带附近激励时所需动力吸振器的安装位置。根据外部激励的宽频转矩模型与系统固有振动之间的关系，切割整个振动频带，针对各个敏感频段安装相应的吸振器。对各个动力吸振器进行最优参数匹配设计，将其安装到传动系统中，进行移频特性和固有振动能量分析。最后针对安装动力吸振器组的动力传动系统进行瞬态振动响应分析，仿真结果表明在相应位置安装动力吸振器组的方法能够非常有效改善系统宽频振动。

1 动力传动系统振动特性分析

将动力传动系统简化为4自由度的扭振系统，发动机为第1个惯量J1，离合器为第2个惯量J2，变速器为第3个惯量J3，随后传动路径为第4个惯量J4。

1.1 固有振动特性分析

动力传动系统4自由度扭振动力学模型如图1所示，系统参数如表1所示。

图1 简化的动力传动系统扭振动力学模型

表1 传动系统参数列表

利用拉格朗日方程计算获得动力学方程：

式中：θ 为各个惯量的角位移，θ=[θ1θ2θ3θ4]；T 为外部激励，T=[T(t) 0 0 0]。 根据动力学公式获得系统的惯量、阻尼和刚度矩阵：

整理得

将有阻尼的自由扭振系统转化为状态空间初值：

对上式进行复特征分析，得到特征值λ和特征向量ψ，最终推导出各阶固有频率及其所对应的振型和阻尼比。获得的第1挡固有频率和对应阻尼比如表2所示。

表2 系统第1挡固有频率和对应阻尼比

由表2可知，动力传动系统存在发动机J1、离合器J2、变速器J3和其它惯量J4，这4个惯量的各自扭转运动分别作为动力学模型的4个自由度[11-13]。通过特征值计算获得系统的4阶固有振动，第1阶固有振动频率为0，是由于该阶固有振动描述整个系统的刚体扭转运动，不存在振动，不做详细考量。而第2阶到第4阶固有振动为系统的主要振动形式，为本文研究重点。

1.2 各阶特征值相对于各个惯量的灵敏度分析

对各阶特征值进行相对于各个惯量的灵敏度分析[14-15]，将第r阶特征值及特征向量代入式(7)，各个转动惯量Jn(n=1，2，3，4)作为灵敏度分析的自变量，并且左乘，求导：

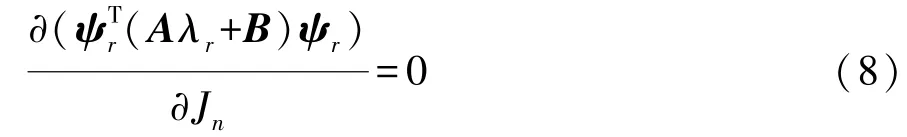
整理得

得到

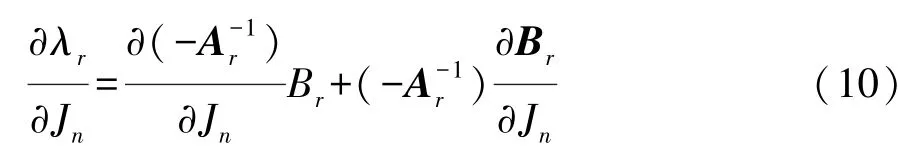
展开：

又因为：

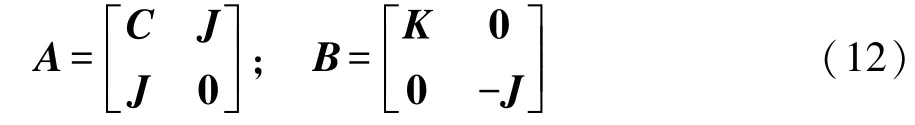
由图2(a)可知，动力传动系统的第2阶振动特性受惯量J1，J2，J3影响很大，在相应位置加装动力吸振器，改变激励频率在第2阶固有频率附近的系统振动；由图2(b)第3阶特征值灵敏度可看出，第3阶振动特性受惯量J3影响最大，如果激励频率在第3阶固有频率附近时，将动力吸振器加装在J3附近，能有效改善该频率范围的振动特性；由图2(c)可知，第4阶振动特性对惯量J2变化敏感，为了控制激励频率在第4阶固有频率附近的振动，可在J2附近加装动力吸振器，以期获得最佳的减振效果。

综上可知，通过研究动力传动系统固有振动特性和灵敏度分析，获得影响动力传动系统各阶固有振动的关键转动惯量，确定各共振频带附近激励时所需动力吸振器的安装位置。

2 振动频带分段

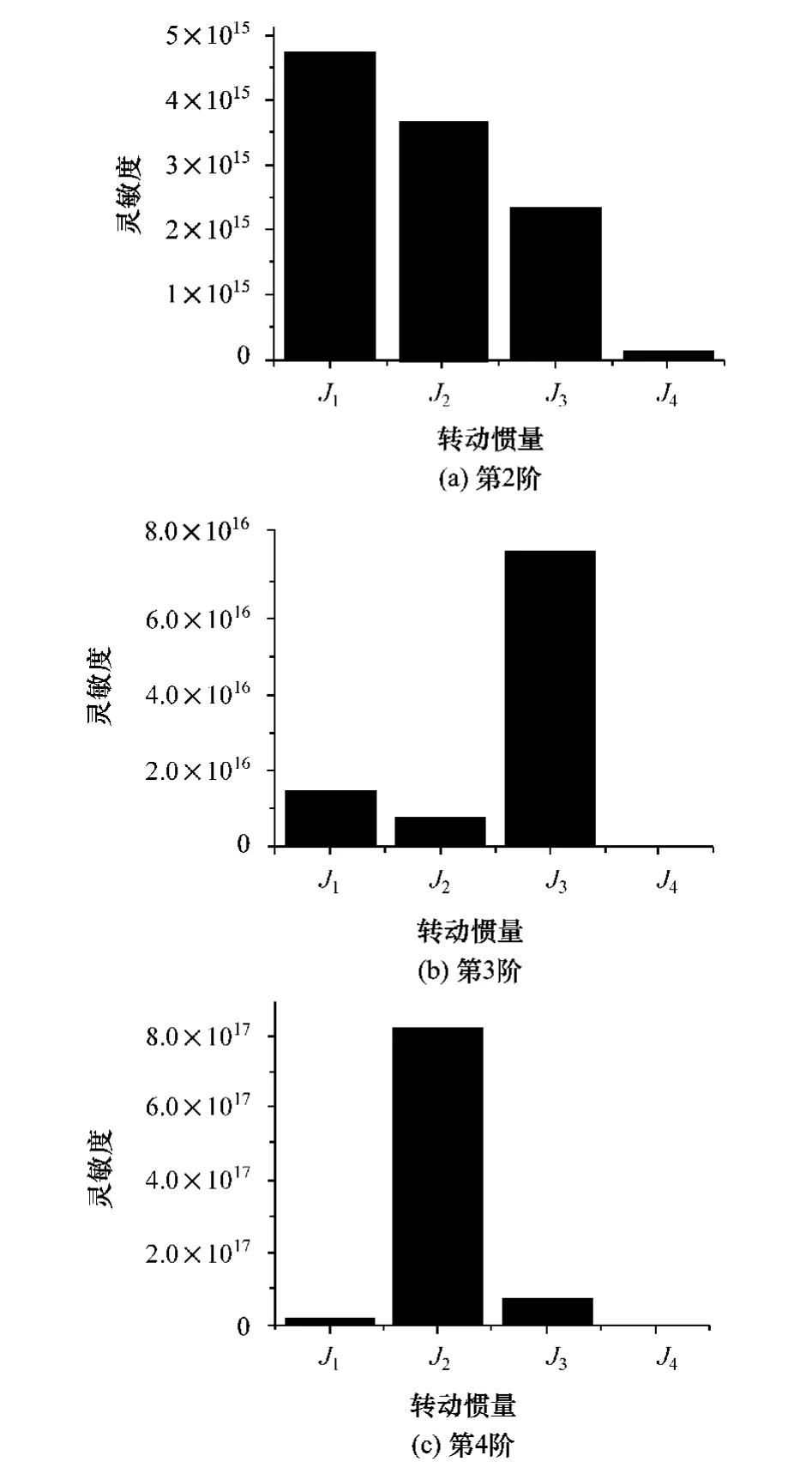
图2 特征值对于各惯量的灵敏度值

对于扭振动力学模型，理论上应该在J1施加一个扭转力矩，在J4施加一个反方向的阻力矩，否则由于系统没有边界约束，会导致计算不收敛。通常情况下，在J1施加的扭转力矩包含两部分，一部分为平均传递转矩，一部分为附加波动转矩。本文中研究重点为动力吸振器组对附加波动转矩的消减作用，针对于此，设计一个均值为0、变频的附加波动转矩激励信号，施加在J1，省略平均传递转矩，相当于给J4端加了一个固定约束[16-18]。

省略平均传递转矩，将瞬态激励转矩模型[16]扩展，改进成穿越动力传动系统所有固有频率的激励信号，在稳态振动时，附加波动转矩频率为一恒定值，而瞬态激励频率会随着时间变化而变化，可以假设波动转矩模型如下：

本模型第1阶段的变频开始于T1=1s，结束于T2=4s，所对应的外部激励转矩的起始振动频率分别为4和20Hz；第2阶段的变频开始于T1=8s，结束于T2=12s，所对应的外部激励转矩的起始振动频率分别为20和40Hz；第3阶段的变频开始于T1=16s，结束于T2=24s，所对应的外部激励转矩的起始振动频率分别为40和80Hz。转矩幅值T0为20N·m。宽频转矩激励与系统固有振动频率的对应关系如图3所示。

图3 宽频转矩激励与固有振动频率关系

由图3可知，当外部激励转频由4升高到20Hz时，转矩信号穿过系统的第2阶固有频率处10.21Hz；当外部激励转频由20升高到40Hz时，转矩信号会穿过系统的第3阶固有频率处28.58Hz；当外部激励转频由40升高到80Hz时，转矩信号会穿过系统的第4阶固有频率处62.47Hz。可将外部激励转频切割成 3 段，即为[4，20]，[20，40]，[40，80]Hz，其分别穿过的系统固有频率为10.21，28.58和62.47Hz。

3 安装最佳参数被动吸振器组后传动系统固有振动性能分析

3.1 各个被动吸振器最佳参数匹配

根据灵敏度分析，在1挡位时，可知动力传动系统第2阶固有共振频率f2=10.21Hz，其受惯量J1影响最大，可在惯量J1附近加装最佳相应固有频率的动力吸振器1；第3阶固有共振频率f3=28.58Hz，其受惯量J3影响最大，可在惯量J3附近加装最佳相应固有频率的动力吸振器2；第4阶固有共振频率f4=62.47Hz，其受惯量J2影响最大，可在惯量J2附近加装最佳相应固有频率的动力吸振器3。确定各动力吸振器的安装位置，如图4所示。

图4 动力吸振器安装位置

由于主系统的阻尼很小，可利用最优频率比、最优阻尼比计算各动力吸振器参数。而动力吸振器的动惯量与主惯量的比值太小，消振效果不明显，比值太大会造成动力损失。可以先确定动惯量与主惯量的比值μ=Ja/Ji=0.2；随后根据最优频率比、最优阻尼比公式计算动力吸振器的最佳刚度和最佳阻尼比。

最终确定各个吸振器的参数如表3所示。

表3 各个吸振器的参数

3.2 移频特性分析

在动力传动系统对应位置安装对应参数的被动吸振器，建立其动力学方程：

式中：θ 为各个惯量的角位移，θ=[θ1θ2θ3θ4θA1θA2θA3]；T 为外部激励，T=[T(t) 0 0 0 0 0 0]。可根据动力学公式获得系统的惯量、阻尼和刚度矩阵：

对上述动力学方程进行有阻尼固有振动特性分析，获得新系统的固有频率，与原系统固有频率对比如表4所示。

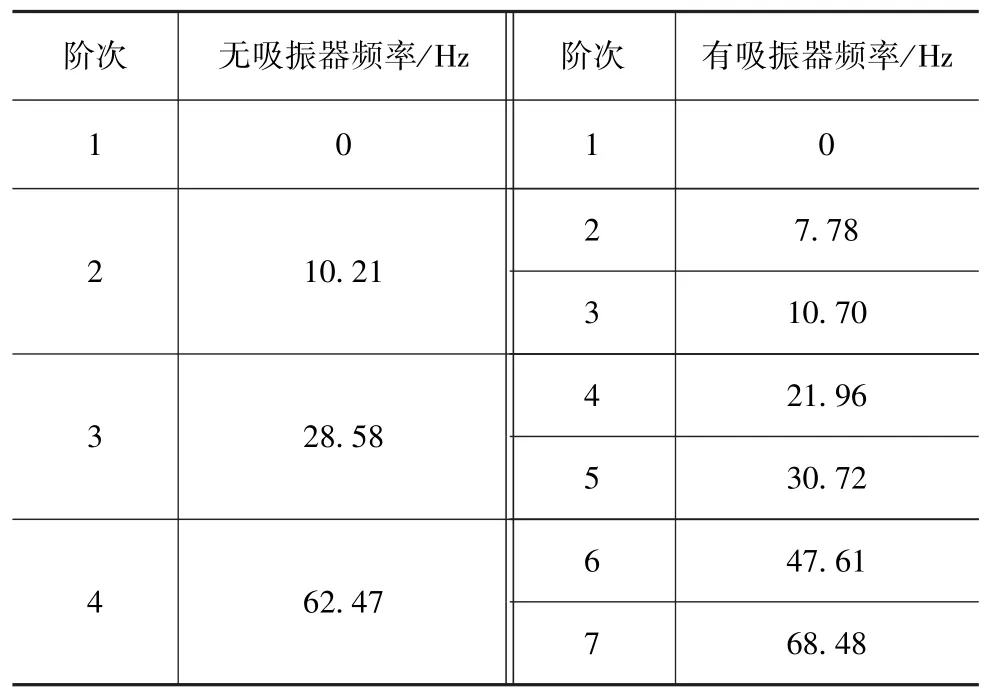
表4 有无吸振器传动系统固有频率对比

由表4可知，传动系统的各阶固有频率在安装动力吸振器之后发生移频，即第2阶固有振动分裂成后来的2，3阶固有振动，其分别所对应的频率为7.78和10.70Hz。第3，4阶固有振动亦出现相似现象。

3.3 振动能量分析

根据振动能量计算公式，可得传动系统在n阶固有振动时最大动能为

展开可得

式中：ωn为第n阶固有振动频率；Jn为对角惯量矩阵相应位置元素；ψnl，ψnk分别为[ψn]的第l，k项元素。

计算获得各阶固有频率处的振动能量，将未安装吸振器与安装吸振器的各阶固有振动能量进行对比，如表5所示。

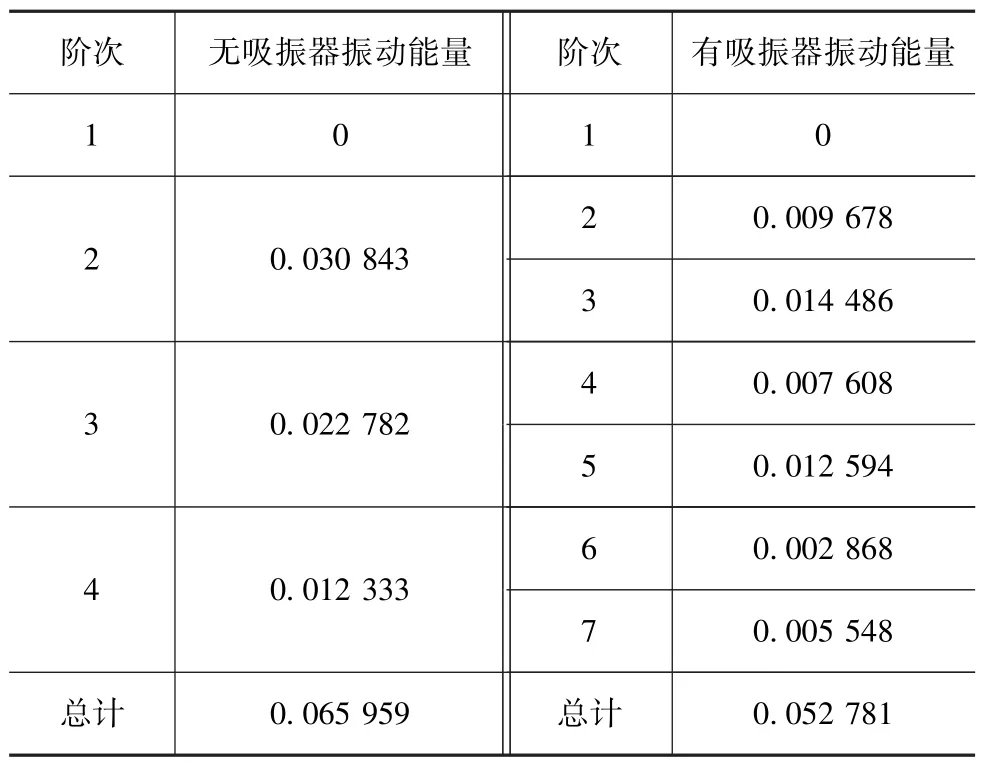
表5 有无吸振器的各阶固有振动能量对比

由表5可知，从各阶固有振动能量角度分析，安装动力吸振器后，无吸振器原有每1阶次在安装吸振器后分裂出2个新的阶次，虽然固有频率的数量增加，即系统的共振峰值数量增加，但对应新分裂出的2个阶次的振动能量之和均小于原有对应阶次的振动能量，且总体的振动能量下降19.98%，从这个角度分析加装动力吸振器后，能达到一个较好的减振效果。

表4和表5呈现的移频特性和振动能量分析结果表明安装吸振器组能够有效减小传动系统振动。佐证了吸振器的减振机理。

4 安装被动吸振器组的传动系统受迫瞬态振动响应分析

当外部激励信号频率在各阶固有振动频率附近时，对应的吸振器对该频段振动进行消减，取T(t)为幅值20N·m、时间为26s的时间历程激励信号。

对于第1阶段变化时间为6s，0～1s为固定频率4Hz的波动转矩激励信号，1～4s时激励信号频率从4匀速增长到20Hz，4～6s为固定频率20Hz的波动转矩激励信号。该频段振动信号穿越动力传动系统原有第2阶固有振动频率，吸振器1可对该频段振动进行消减。

第2阶段变化时间为 8s，6～8s为固定频率20Hz的波动转矩激励信号，8～12s时激励信号频率从20匀速增长到40Hz，12～14s为固定频率40Hz的波动转矩激励信号。该频段振动信号穿越动力传动系统原有第3阶固有振动频率，吸振器2可对该频段振动进行消减。

第3阶段变化时间为12s，14～16s为固定频率40Hz的波动转矩激励信号，16～24s时激励信号频率从40匀速增长到80Hz，24～26s为固定频率80Hz的波动转矩激励信号。该频段振动信号穿越动力传动系统原有第4阶固有振动频率，吸振器3可对该频段振动进行消减。

对动力系统进行宽频瞬态振动分析，得到有无吸振器两个转动惯量的相对角位移响应时间历程曲线，如图5所示。

图5 θ2-θ1相对角位移时间历程曲线

由图5可知：无吸振器的动力传动系统在1～4s，8～12s和19～24s 3 个时间段，振动幅值较大，其中1～4s时间段振动最为明显，最高达到0.011rad，3个时间段均为激励频率瞬时变化阶段，说明激励频率的瞬时变化会使得传动系统振动恶化，该结果表明安装动力吸振器必要性；安装动力吸振器组后，系统在1～4s，8～12s和19～24s 3个时间段振动明显下降，1～4s振动幅值由原来的1.1×10-2rad下降到4.1×10-3rad，下降62.7%，其它激励频率的瞬时变化阶段的振动均有明显改善。然而在4～8s时间段，无动力吸振器的传动系统振动本来就很小，安装被动吸振器组的振动反而呈现恶化趋势，关于减小4～8s时间段振动的问题需进一步深入研究。

5 结论

(1)建立车辆动力传动系统4自由度的扭振动力学模型，对系统进行固有振动特性分析，根据特征值灵敏度分析结果，得到影响系统各阶固有振动的关键转动惯量，并确定各共振频带附近激励时所需动力吸振器的安装位置。

(2)建立外部激励的宽频转矩模型，分析其与系统固有振动之间的关系，将整个振动频带切割分段，针对各个敏感频段安装相应的吸振器，进行吸振器最佳参数匹配。对安装吸振器组传动系统进行了移频特性和振动能量分析。

(3)对安装被动吸振器组的动力传动系统进行受迫瞬态振动响应分析，通过对比有无吸振器两个转动惯量的相对角位移响应的时间历程曲线，证明安装吸振器组方法能够有效减小传动系统宽频振动。