从中考数学大纲看动点问题

赵 钦

（贵州省遵义市桐梓县芭蕉镇芭蕉中学，贵州 遵义563209）

动点几何问题出题范围不仅仅涉及到点线面，还涉及到各种几何图形，例如：平行四边形、梯形、三角形等，中学动点几何也是常常与函数的使用联系在一起，需要我们视为重点来分析。所以说，动点问题是中考数学当中的重中之重，只有学生不断学习和理解，并完全掌握，才有机会拼得高分。

一、动点几何问题的特点

动点几何是以几何知识和几何图形为最基础的背景，运用运动变化的重要观点，进一步研究几何图形中图形的位置、角与角、线段与线段的位置及它们的大小，让他们有规律的变化，其中有些量一直保持不变，称作定值，也就是变与不变的问题，解题的时候要数形结合，具有较强的综合性，而且考试题目灵活多变，可以说是动中有静，动静结合。动点几何问题的学习与解决，有助于学生发展空间想象力，培养综合分析能力。

二、动点几何问题的解决方法

要解决动点几何问题，首先是要学会观察，对动点变化的规律进行探索，发现变量与定量之间的关系。动点几何函数问题的基本思路是“变动为静，以静探动”。第一步根据点运动或图形运动的路径的特点进行分类讨论，转化形成各类相对静止问题；第二步是通过图形的几何性质及相关几何元素间的关系，建立两个几何变量间的函数关系式。第三步就是确定自变量的取值范围。最后一步就是运用所建函数关系式解决相关问题。

在由几何图形运动建立的函数关系式应用中，要学会试着全方面的进行分析思考，即综合思考，要求对于存在性问题要注意题目条件和存在的多种可能性。

三、动点几何问题的分类

动点几何问题从图像可分为直线型和曲线型；从研究对象可分为点动，线动，面动；从运动形式可分为平移几何题，翻折几何题，旋转几何题，滚动几何题；从运动可分为动点类，动直线类，动图形类……

四、动点几何在函数中的应用

动点几何形成的函数关系和图象问题是动点几何中的基本问题，其考试重点放在动点和动线形成的函数关系和图象问题。

如图，对称轴为直线false的抛物线经过点A（6，0）和B（0，4）.

（1）求抛物线解析式及顶点坐标；

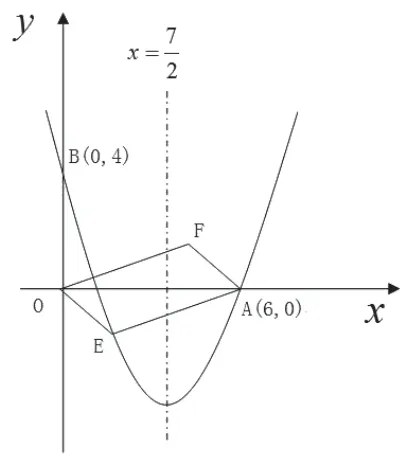
（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；

①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？

②是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由。

（2）∵点E（x，y）在抛物线上，位于第四象限，且坐标适合

∴y＜0，即 －y＞0，－y表示点E到OA的距离.

∵OA是□OEAF的对角线，

因为抛物线与x轴的两个交点是（1，0）的（6，0），所以，自变量x的取值范围是1＜x＜6.

故所求的点E有两个，分别为E1（3，－4），E2（4，－4）.

点E1（3，－4）满足OE = AE，所以□OEAF是菱形；

点E2（4，－4）不满足OE = AE，所以□OEAF不是菱形.

②当OA⊥EF，且OA = EF时，□OEAF是正方形，此时点E的坐标只能是（3，－3）.而坐标为（3，－3）的点不在抛物线上，故不存在这样的点E，使□OEAF为正方形.

结语：

动点几何问题如此有趣多变，它让数学变得充满活力，让数学变得精彩纷呈。而且，对于遵义动点题是近年来中考的的一个热点问题，所以，为了克服学习中的弱点，动点几何的解决更应该受到学生和老师的重视，归纳答题技巧，巩固知识点，进一步理解和掌握关于动点几何的内容。