吊弦振动频率及幅度对疲劳寿命的影响分析

彭培火，陈立明，王伟，何凡



吊弦振动频率及幅度对疲劳寿命的影响分析

彭培火1，陈立明2，王伟2，何凡1

(1. 北京建筑大学 理学院力学系，北京 102612；2. 中国铁道科学研究院标准计量研究所，北京 100015)

推导吊弦的振动方程，用数值方法求解振动方程，模拟位移，横截面作用力和弯矩的动态变化规律。根据吊弦的应力时程、利用MATLAB数值计算程序分析影响吊弦疲劳寿命的因素(如振幅和频率)。数值计算结果表明：吊弦疲劳寿命的对数值随着频率和振幅的增加呈现出线性降低的趋势。

吊弦；振动方程；有限差分法；应力时程；疲劳特征

接触网是电气化铁路牵引供电系统的重要组成部分。吊弦是整个接触网的“支架”，是接触线、承力索之间振动和力的传递者，是供电接触网安全运营的关键零部件。在高速铁路实际运营中，由于随机风场的作用，或受电弓在运行中产生强烈振动，或高铁列车顶部的垂向位移激扰等，会引起吊弦的强烈振动。作用在吊弦上的循环应力极易引起疲劳破坏，发生吊弦断股或断裂的现象。如：2003年2月9日，京广线许昌—孟庙段接触网在暴风雪作用下，剧烈振动，吊弦折断211根[1]。吊弦一旦发生断裂，将直接导致列车运行故障。因此，对吊弦等接触网零部件的疲劳特性的研究具有十分重要的意义。在供电接触网系统的疲劳特征研究方面，诸多学者进行大量的工作。王晓阳等[2]利用ANSYS有限元软件，采用直接积分法对弓网耦合系统进行动态仿真，得到接触线的应力时程，通过简化方法估算获得材料曲线，最终运用线性累积损伤理论对接触线的疲劳寿命进行研究。毕继红等[3−4]采用雨流计数法及Miner线性疲劳累积损伤理论计算得到接触线各单元的疲劳寿命，对跨距、接触线和承力索预张力、截面面积、列车行驶速度、抬升力、干摩擦等因素对接触线疲劳寿命的影响进行研究。宋洋等[5]采用Davenport和Panosfsky功率谱对作用在接触网上的随机脉动风时程进行模拟，推导了作用在接触网上的气动力，对随机风场下高速铁路接触线风振疲劳进行研究。在实际运营过程中，接触网承受着不同振幅和频率的交变载荷。如随机风载荷的脉动频率变化，或风速的大小引起吊弦振动幅度变化，或列车的运行速度变化对接触网的干扰更加频繁，或在受电弓的抬升作用下，接触线的抬升量导致不同的振动幅度等，吊弦在这些因素的影响下，都可能表现出不同的疲劳特性。本文研究吊弦的振动幅度、振动频率对吊弦疲劳寿命的影响。首先将吊弦简化成在轴力、剪力与弯矩综合作用下的组合变形构件，推导吊弦振动的微分方程组；其次采用数值求解的方法，将微分方程转化成差分方程，并利用MATLAB软件，编写求解吊弦各个单元的应力时程的代码以及弯矩、轴力、截面应力的可视化程序；然后基于巴斯坎(Basquin)方程得出的双对数曲线图和Palmgren–Miner线性疲劳累积损伤准则，利用由MATLAB编写的疲劳寿命计算程序，通过改变数值计算的参数，对数值结果进行分析比较，研究以上因素对吊弦的疲劳行为的影响。

1 吊弦动应力计算

在高铁列车供电弓网系统的实际运营过程中，当接触网处于静止状态时，吊弦承受由接触线恒定负载引起的拉伸载荷，吊弦处于拉伸状态；当列车通过时，在受电弓的抬升作用下吊弦处于松弛状态；列车通过后，在接触线恒定负载的作用下吊弦回到拉伸状态。每一次受电弓通过，吊弦完成一次周期振动。可以将吊弦在实际工况下的振动等效为在吊弦与承力索连接点的简谐振动激励下引起的受迫振动，在吊弦的下端作用有一个由于接触线重量产生的竖直向下的恒定的作用力(如图1 所示)[6]。

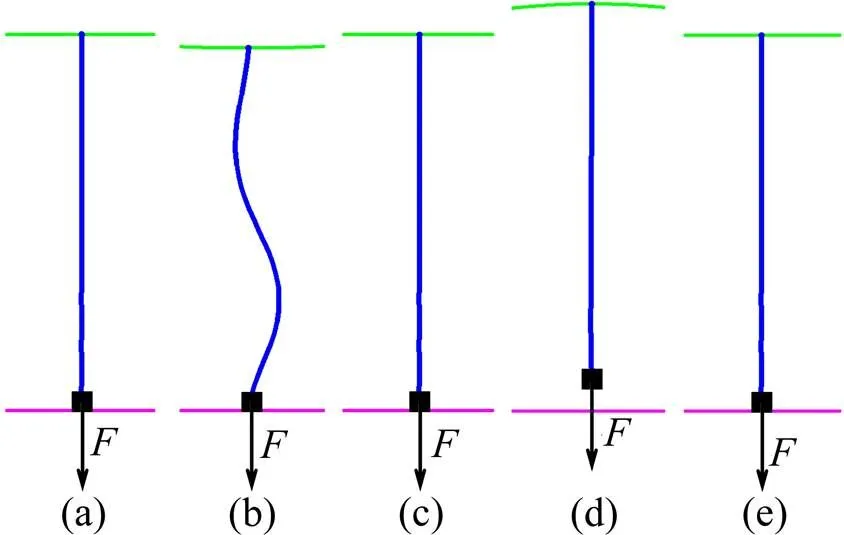
图1 吊弦疲劳原理

1.1 吊弦振动方程的推导

为了计算吊弦在上述等效实验工况下的应力状态，从其中取一段吊弦微元进行受力分析，如图2所示。

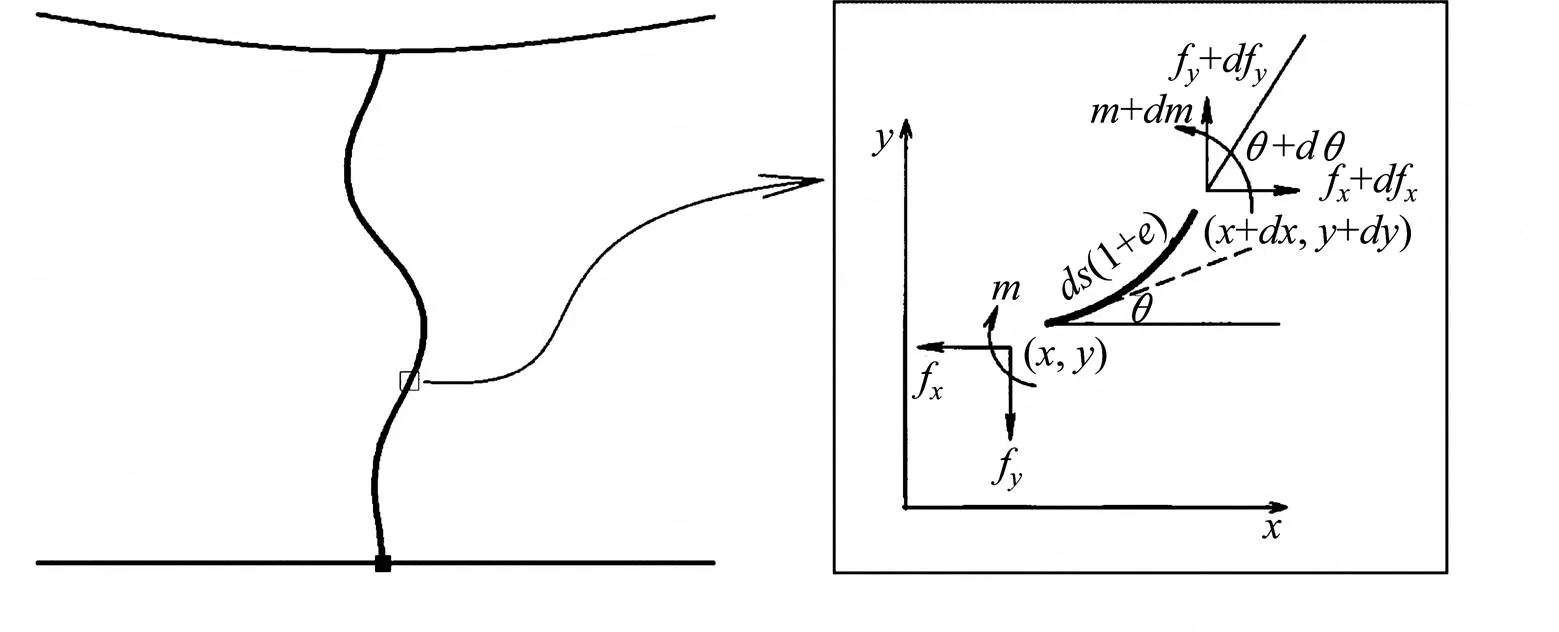
图2 吊弦微元段受力分析

为计算上的简化和方便，引用以下无量纲 变量：

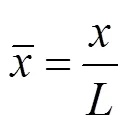
其中：表示吊弦的总长度；表示吊弦的密度；v表示方向的运动速度；v表示方向的运动速度；表示重力加速度；为弯矩；为抗弯刚度；为吊弦的弹性模量；为吊弦的横截面积；为弧长坐标；为吊弦微元段与轴之间的夹角；f和f分别为吊弦上的作用力沿方向和方向的分量，正负号约定如图2中所示。

根据吊弦微元段的受力和运动，可以得到如下的方程组：

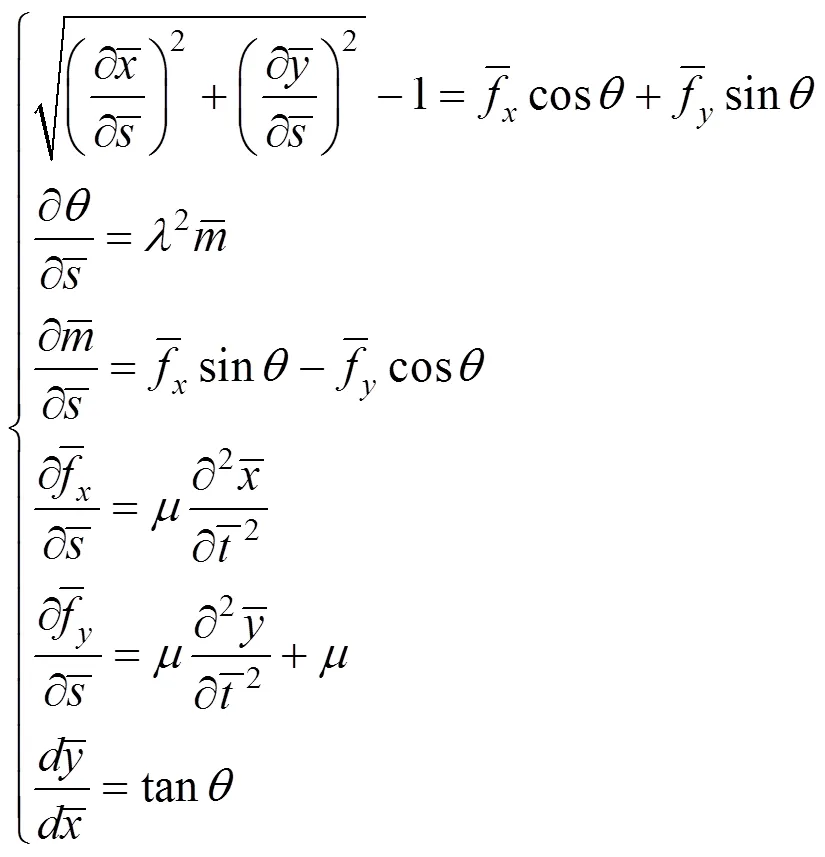
初始条件可以表示为：

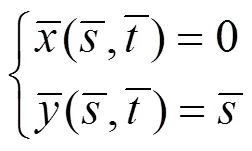
边界条件可以表示为：

1.2 数值求解方法

方程组(1)为一组非线性偏微分方程，本文通过数值方法将微分方程转换为差分方程，利用MATLAB编写代码求解差分方程组，最后求得吊弦运动的数值解。

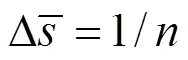
1.3 计算参数

针对吊弦实际使用的铜绞线，在WDW−100型微机控制电子万能材料试验机上，利用电子引伸计测试轴向变形，进行弹性模量的测试实验(如图3所示)，测得其弹性模量为83.29 GPa。由于铜绞线是由多根铜丝绞合构成的，其弯曲刚度并不能简单地等同于弹性模量乘以横截面的惯性矩。早在1997年，Costello[7]就研究了绞线的宏观力学行为，并推导了绞线弯曲刚度的计算公式。XING 等[8]利用ABAQUS建立的绞线有限元模型研究绞线的弯曲行为，得到不同螺旋角下绞线的等效抗弯刚度，计算结果与Costello模型接近。本文中吊弦的抗弯刚度参数基于Costello模型计算得出。由于吊弦振动过程中，截面应力主要由拉伸引起(通过比较考虑弯曲应力和不计入弯曲应力两者之间的差别，可以发现弯曲应力的影响可以忽略)。铜绞线的弹性模量是利用万能材料试验机和电子引伸计直接测量得到的，可以保证抗拉刚度的计算参数是精确的。数值计算中各参数的具体取值如表1所示。

为了分析激励频率及振幅对吊弦截面应力的影响，利用MATLAB编写了可视化程序，对吊弦振动过程中的弯矩、轴力和截面应力等实施动态显示，可视化界面如图4~5所示。

图3 测试铜绞线的弹性模量

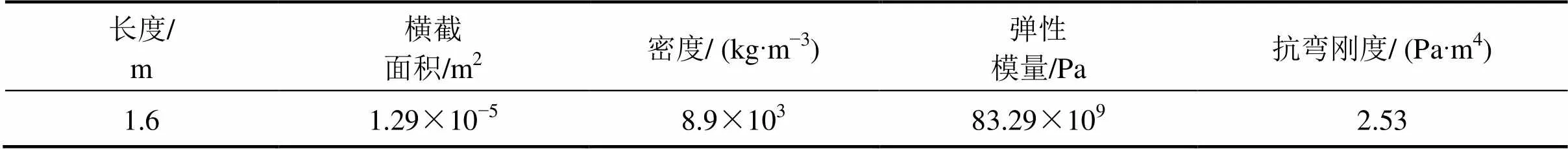
表1 数值计算中所采用的吊弦参数

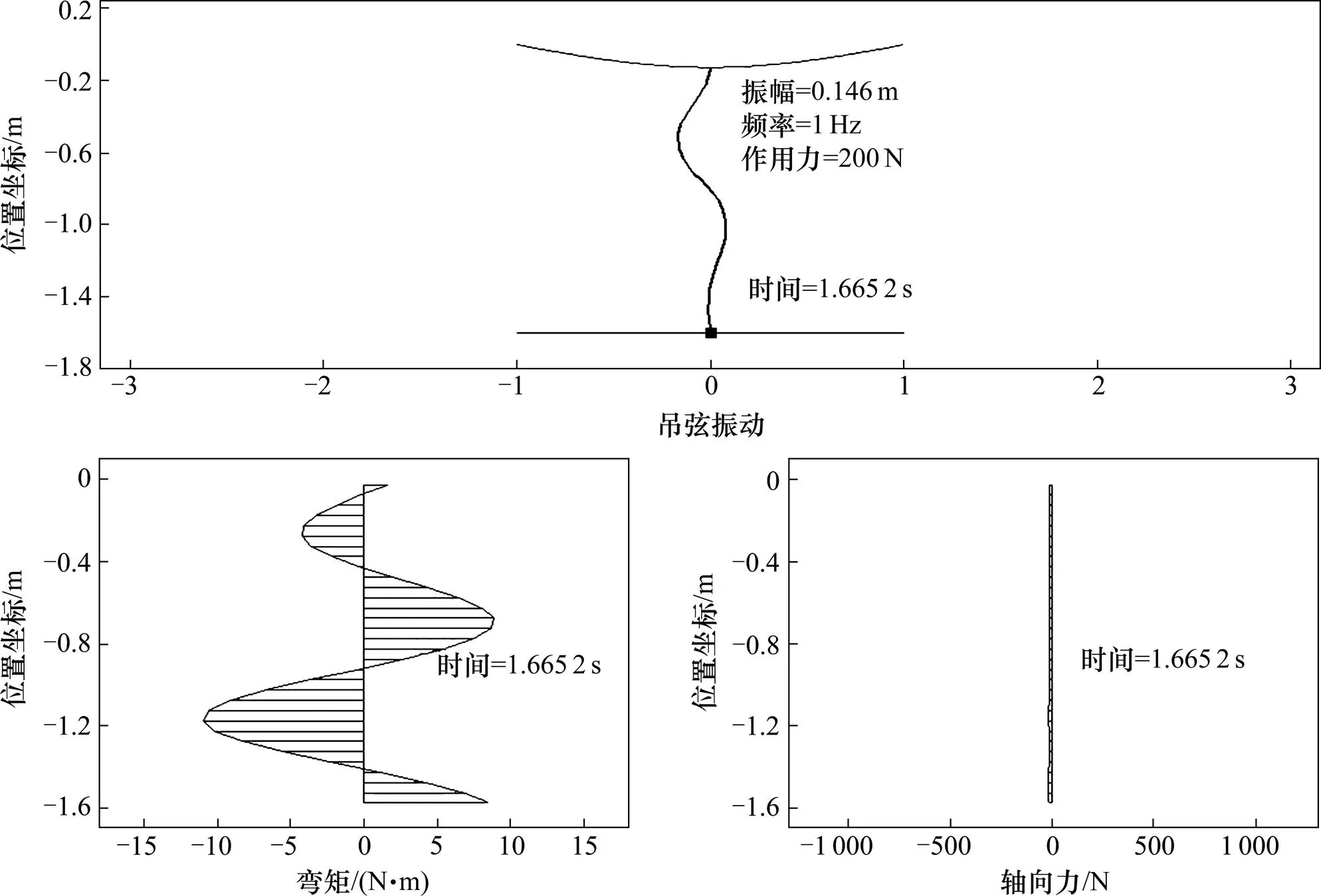
图4 吊弦动态振动过程、弯矩图与轴力图

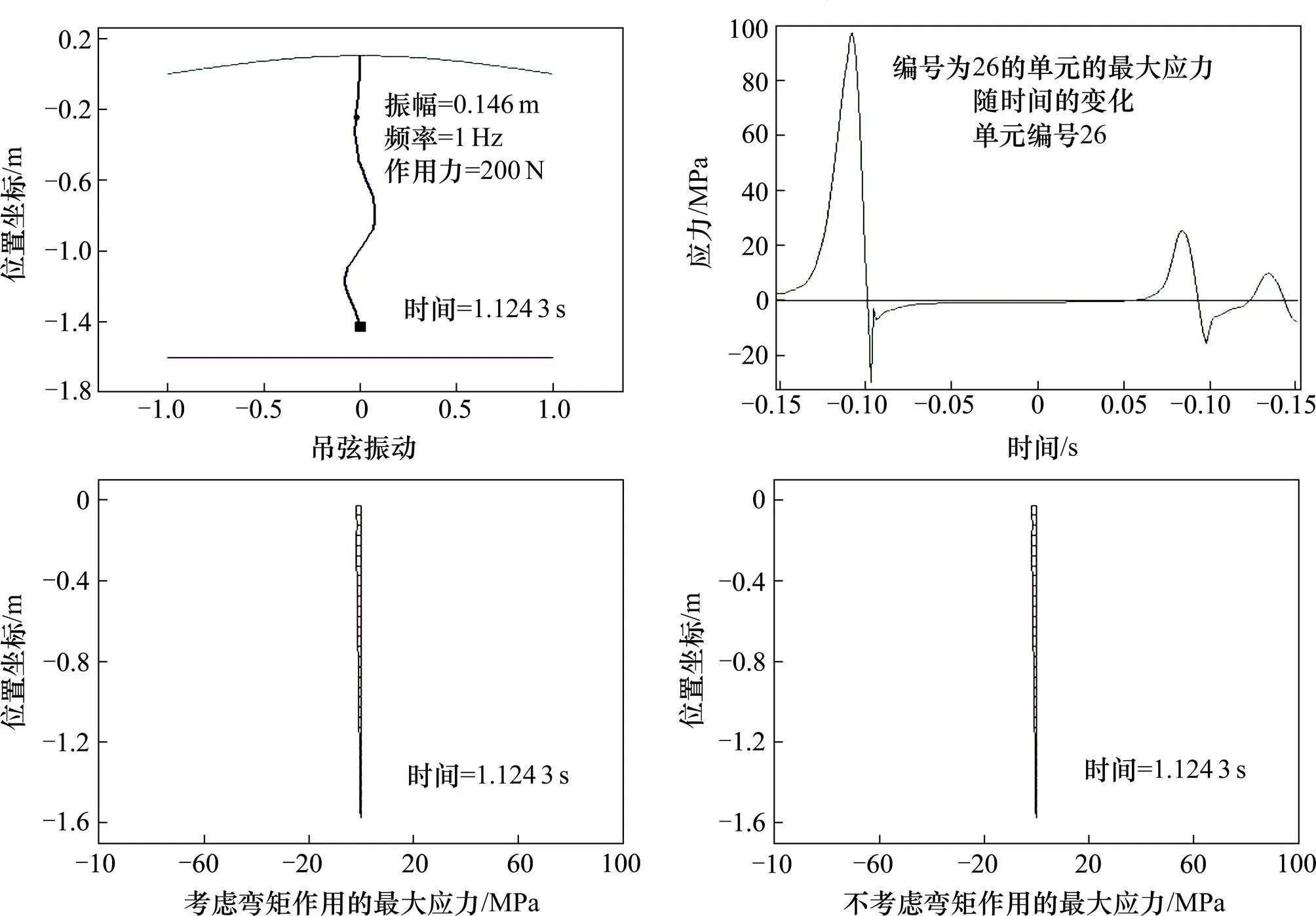
图5 吊弦动态振动过程、截面应力的变化过程

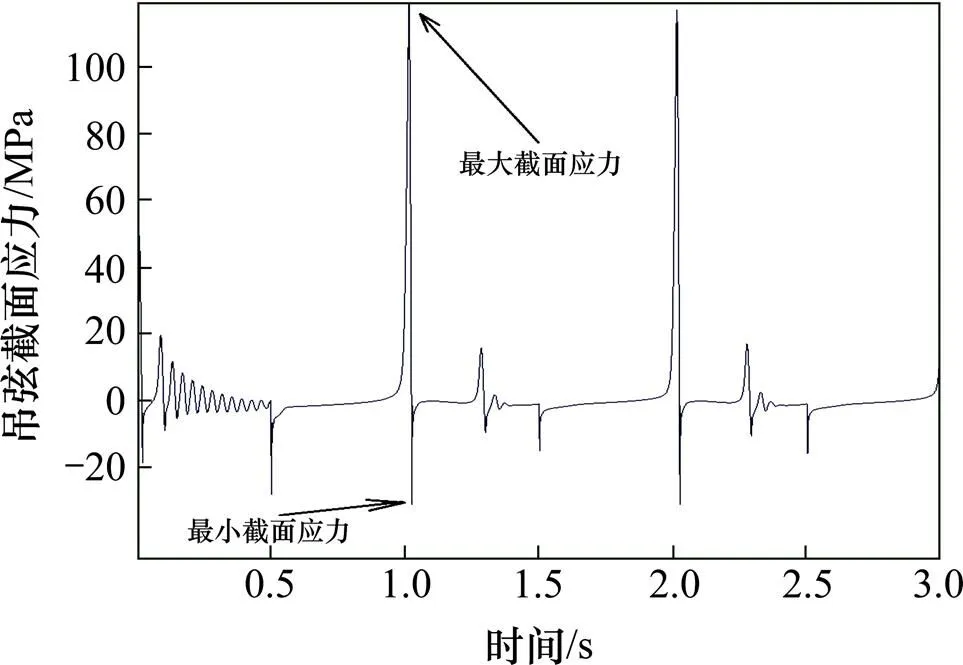
图6 吊弦截面应力随时间的变化过程

从图6可以看出，驱动点按简谐振动方程振动，随着驱动点上抬，吊弦线被拉紧，应力发生减幅波动。当驱动点向下运动到原点时，吊弦开始松弛弯曲，瞬时受到较大的冲击压应力，随之便迅速减小。在将吊弦拉直之前，其截面应力一直保持较小的压应力。在驱动点向上运动的过程中，在将吊弦拉直的瞬时，吊弦受到非常大的冲击应力，此时的拉应力数值为整个振动过程中的最大拉应力。在随后的振动过程中，驱动点按简谐振动往复循环运动，吊弦的截面应力基本也保持这样的规律按相同的周期循环变化。

1.4 数值结果分析

1.4.1 振动频率对吊弦截面应力的影响

通过将振幅固定为0.035 m，作用力固定为100 N，改变振动频率进行计算分别得到吊弦截面在不同激励频率下的应力时程。统计在各个频率下的最大和最小截面应力(如图7所示)，可以看到，当频率小于2.4 Hz时，最大截面应力随频率的增大而增大，最小截面应力随频率的增大而减小，二者都基本呈线性变化。当激励频率大于2.4 Hz之后，应力与频率的关系变得复杂。通过对吊弦振动的动态过程仔细观察，发现这是由于吊弦下端质量的运动幅度变得非常大，从而导致吊弦由弯曲松弛变为拉直张紧的瞬时并不是发生在驱动点过原点时，此时吊弦下端质量与驱动点之间的相对速度与频率的关系较为复杂，而瞬时冲击力与该相对速度是密切相关的，于是最大应力与频率之间不再呈现简洁的线性关系。

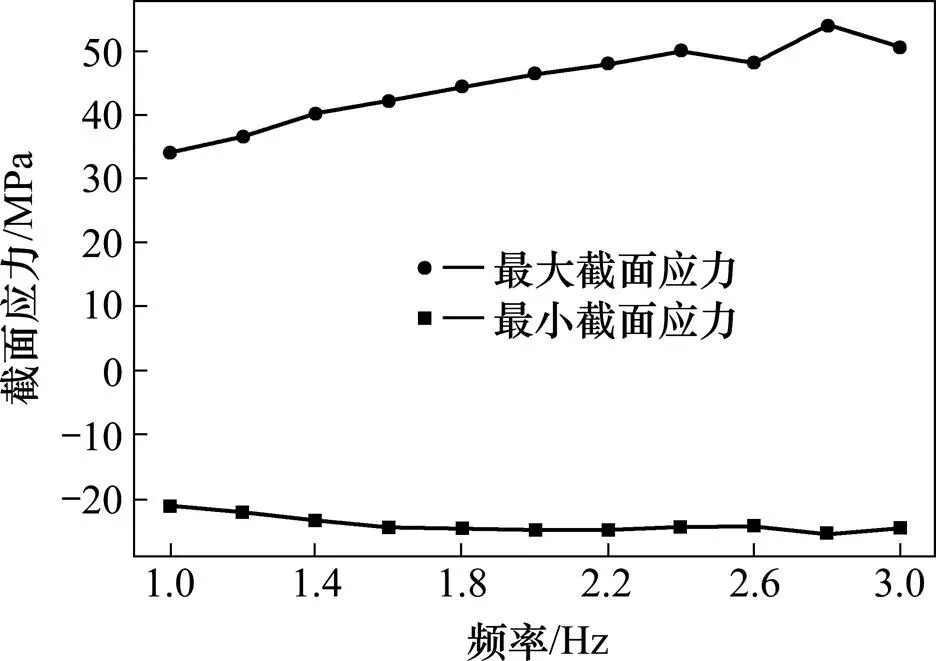
图7 吊弦截面的最大、最小应力与激励频率的关系

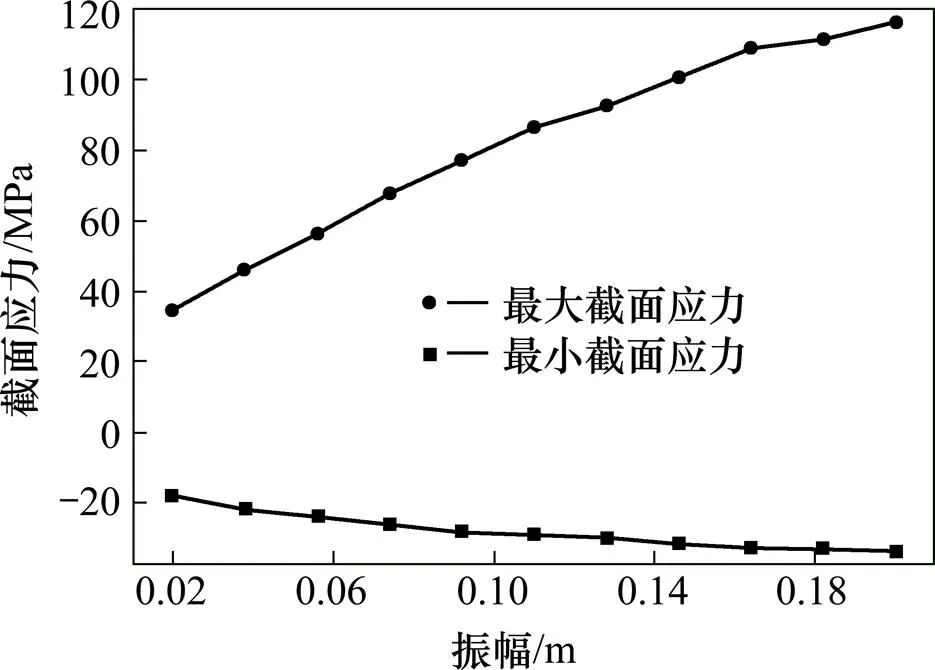
图8 吊弦截面的最大、最小应力与振幅的关系

1.4.2 振幅对吊弦截面应力的影响

将作用力固定为200 N，激励频率固定为1 Hz，通过改变振幅分别进行计算得到吊弦在不同振幅下的应力时程。统计在各个振幅下的最大和最小截面应力如图8所示。为了定量分析应力与振幅之间的线性相关性，分别计算振幅与最大截面应力之间的线性相关系数1=0.989 8≈1，振幅和最小截面应力之间的线性相关系数2=−0.969 2≈−1。从计算结果可以看到，最大和最小截面应力均与振幅呈非常好的线性关系，最大截面应力随振幅的增大而线性增大，最小截面应力随振幅的增大而线性减小。

2 吊弦疲劳寿命分析

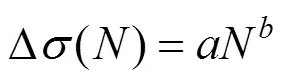
2.1 振动频率对疲劳寿命的影响

计算当振幅和作用力固定(振幅为0.035 m，作用力为100 N)，加载频率变化时吊弦截面的应力时程曲线。根据以上各个加载频率下吊弦截面的应力时程曲线，可以计算出吊弦的疲劳寿命，计算结果如图9所示。由于疲劳寿命的跨度较大，纵坐标采用对数表示。从图9可以看出，当频率小于2.4 Hz时，吊弦疲劳寿命的对数值log与激励频率之间保持较好的线性关系，随着频率的增大而降低。当频率大于2.4 Hz时，由于前述原因，疲劳寿命也出现了一定的波动，其对数值也不再简单地线性 降低。

2.2 振幅对疲劳寿命的影响

根据当加载频率和作用力固定，各不同振幅下的应力时程曲线，可以计算出吊弦的疲劳寿命，计算结果如图10所示。从图10可以看出，吊弦疲劳寿命的对数值log与振幅基本呈线性关系，随着振幅的增大而线性降低。

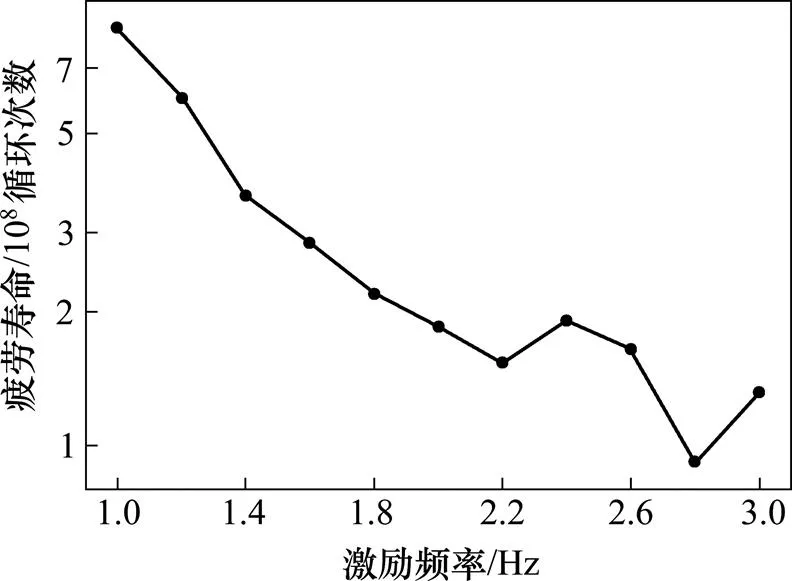
图9 吊弦疲劳寿命随加载频率的变化规律

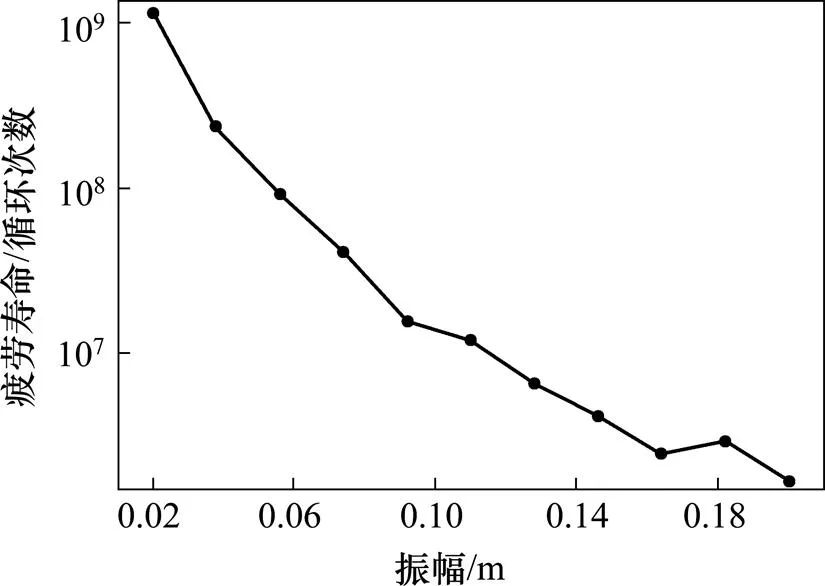
图10 吊弦疲劳寿命随振幅的变化规律

3 结论

1) 吊弦截面的最大应力出现在吊弦由弯曲松弛变为拉直张紧的瞬时，且随着振动频率和振幅的增加而线性增加。最小应力出现在紧随最大应力之后，吊弦下端的质量由于惯性向上急剧上升引起吊弦压缩的瞬时。最小应力随着振动频率、振幅的增加而线性减小。

2) 当振动频率较小时，吊弦疲劳寿命的对数值基本与振动频率呈线性关系；当振动频率较大时，吊弦疲劳寿命不再随频率的增加而线性降低，而是出现上下波动。这与频率较大时吊弦的应力时程的变化密切相关。

3) 从数值模拟的结果上看，吊弦疲劳寿命的对数值与振动幅度呈较好的线性相关性，随着振动幅度的增加而线性降低。

[1] 班瑞平. 接触网线索舞动现象的研究[J]. 铁道机车车辆, 2004, 24(1): 64−66. BAN Ruiping. Research on phenomena of the contact line brandishing[J]. Railway Locomotive & Car, 2004, 24(1): 64−66.

[2] 王晓阳, 张卫华, 李瑞平, 等. 基于名义应力法的弹性链型接触网疲劳寿命预测[J]. 计算机辅助工程, 2014, 23(6): 7−12. WANG Xiaoyang, ZHANG Weihua, LI Ruiping, et al. Fatigue life prediction of elastic stitched catenary based on nominal stress method[J]. Computer Aided Engineering, 2014, 23(6): 7−12.

[3] 毕继红, 陈花丽, 任洪鹏. 基于雨流计数法的接触线疲劳寿命分析[J]. 铁道学报, 2012, 34(6): 34−39. BI Jihong, CHEN Huali, REN Hongpeng. Analysis on fatigue life of contact wire based on rain-flow counting method[J]. Journal of the China Railway Society, 2012, 34(6): 34−39.

[4] 毕继红, 任洪鹏, 陈花丽. 基于雨流计数法的弹性链型柔性悬挂接触网疲劳寿命分析[J]. 铁道科学与工程学报, 2012, 9(1): 61−67. BI Jihong, REN Hongpeng, CHEN Huali. The fatigue analysis on the elastic chain flexible suspension catenary system based on rain-flow counting[J]. Journal of Railway Science and Engineering, 2012, 9(1): 61−67.

[5] 宋洋, 刘志刚, 汪宏睿, 等. 随机风场下高速铁路接触线风振疲劳分析[J]. 铁道学报, 2015, 37(7): 20−26. SONG Yang, LIU Zhigang, WANG Hongrui, et al. Analysis on influence of stochastic wind field on wind vibration fatigue of high-speed railway catenary[J]. Journal of the China Railway Society, 2015, 37(7): 20− 26.

[6] 王伟, 吴积钦, 关金发, 等. 高速铁路接触网吊弦疲劳试验台[J]. 高速铁路技术, 2014, 5(3): 22−25. WANG Wei, WU Jiqin, GUAN Jinfa, et al. A fatigue test rig of high-speed railway catenary dropper[J]. High Speed Railway Technology, 2014, 5(3): 22−25.

[7] Costello A G. Theory of wire rope[M]. New York: Springer, 1997: 1−50.

[8] XING E, ZHOU C. Analysis of the bending behavior of a cable structure under microgravity[J]. International Journal of Mechanical Sciences, 2016, 114: 132−140.

[9] Nasution F P, Sævik S, Berge S. Experimental and finite element analysis of fatigue strength for 300 mm2copper power conductor[J]. Marine Structures, 2014, 39: 225− 254.

[10] Aid A, Amrouche A, Bouiadjra B B, et al. Fatigue life prediction under variable loading based on a new damage model[J]. Materials & Design, 2011, 32(1): 183−191.

[11] Pereira HlFSG, De Jesus AlMP, Ribeiro A S, et al. Cyclic and Fatigue Behavior of the P355NL1 steel underblock loading[J]. Journal of Pressure Vessel Technology, 2009, 131(2): 021210.

[12] Santecchia E, Hamouda A M S, Musharavati F, et al. A review on fatigue life prediction methods for metals[J]. Advances in Materials Science and Engineering, 2016, 2016: 9573524.

The effect of frequency and amplitude of dropper on its fatigue life

PENG Peihuo1, CHEN Liming2, WANG Wei2, HE Fan1

(1. Department of Mechanics, School of Science, Beijing University of Civil Engineering and Architecture, Beijing 102612, China; 2. Standards & Metrology Research Institute, China Academy of Railway Sciences, Beijing 100015, China)

First, the vibration equation of dropper was derived. Then the dynamic change laws of displacement, cross-sectional force and bending moment were simulated by solving vibration equation with numerical method. According to the stress-time curve, the factors affecting the fatigue life of dropper (such as amplitude, frequency) were analyzed by using the MATLAB code. The results of numerical calculation show that the logarithm of the fatigue life decreases linearly with the increase of frequency and amplitude.

dropper; vibration equation; finite difference method; stress-time curve; fatigue characteristics

10.19713/j.cnki.43−1423/u.2019.02.025

U225.4

A

1672 − 7029(2019)02 − 0471 − 07

2018−01−08

中国铁路总公司科技研究开发计划资助项目(2017J010-A)

何凡(1979−)，男，江西南昌人，副教授，博士，从事工程力学研究；E−mail：hefan@bucea.edu.cn

(编辑 阳丽霞)