土坡稳定分析中考虑参数变异水平的分项系数取值
2019-03-07李昂罗强张文生蒋良潍张良
李昂,罗强,张文生,蒋良潍,张良
土坡稳定分析中考虑参数变异水平的分项系数取值
李昂1, 2,罗强1, 2,张文生1, 2,蒋良潍1, 2,张良1, 2
(1. 西南交通大学 土木工程学院,四川 成都 610031; 2. 高速铁路线路工程教育部重点实验室,四川 成都 610031)
岩土参数变异性大导致可靠指标离散性高,仅用1组分项系数难以保证土工结构可靠性达到目标可靠度。将土体强度参数变异性划分为小、中、大3个水平,以现有规范规定安全系数为控制指标,对常见铁路路堤边坡目标可靠度进行校准,确定目标可靠指标为2.3;运用验算点法计算分项系数,讨论几何和强度参数对分项系数影响规律,通过统计分析及标定得到了对应3种变异水平的分项系数推荐值。研究结果表明:土体强度参数变异性是影响分项系数取值的主导因素,强度参数均值和坡高次之,坡率的影响较为微弱;为使强度参数变异性不同的边坡达到一致的可靠度,提出了分项系数应与参数变异水平相适应的取值原则,给出了小、中、大变异水平对应的抗力项和荷载项分项系数(γ1,γ2,γ)推荐值分别为(0.75, 0.95; 1.02),(0.55, 0.90; 1.06)和(0.40, 0.80; 1.10)。
土坡稳定分析;参数变异水平;分项系数;目标可靠指标;验算点法
由于复杂地质作用和漫长形成过程,天然土工材料性质具有较大变异性[1−2],如何合理考虑土工参数大变异特性是岩土工程设计面临的最主要的难题之一。传统岩土工程设计方法主要是安全系数法,但岩土材料较高的变异性使得单一安全系数无法反映工程真实安全程度[3]。WU等[4]在1970年首次将可靠度设计方法引入到边坡稳定分析中,并成为边坡设计的主要发展方向。可靠度直接设计法主要有Monte Carlo法和一次二阶矩法等,这些方法虽然可得到结构可靠度,但计算较为复杂繁琐,不利于实际工程应用。基于可靠度理论的分项系数极限状态法保留了容许应力法设计表达式的形式,通过分项系数将检算结果与可靠度联系起来,准确反映结构的安全程度,且计算简单方便,已被广泛应用于结构工程,而铁路工程尚处于研究阶段。工程结构设计方法的落后为中国铁路走向海外带来了诸多困难[5],推动铁路工程结构设计方法从安全系数法向极限状态设计法转变是当前面临的重要任务。对此,国内许多学者对土坡极限状态设计分项系数开展了研究。王仲锦等[6]对铁路路基边坡分项系数取值进行了研究,给出了一套分项系数以及调整式,但文中变异系数取值属于小变异水平,未考虑参数大变异的情况;张宁等[7]讨论了土坡稳定分析分项系数取值,但采用的功能函数为非显式形式,计算较为复杂,不利于工程应用。土工参数变异水平是影响边坡可靠度的最重要因素[8]。《铁路路基极限状态法设计暂行规范》[9]中提供了铁路路堤边坡极限状态设计分项系数建议值,但由于土工参数变异性大且变异范围宽,仅使用1组分项系数无法使具有不同变异水平的边坡达到一致的稳定可靠度。若使用小变异条件下计算所得分项系数对土体大变异的边坡进行设计会使得边坡稳定可靠指标无法达到目标可靠指标,安全程度不足;反之会使得边坡稳定可靠指标远大于目标可靠指标,设计过于保守。因此需要对土工参数变异性进行划分,研究土体不同变异水平下边坡极限状态设计分项系数取值。以现有规范规定断面和安全系数为控制指标,对铁路路堤边坡目标可靠度进行校准。采用验算点法计算分项系数,分析土体强度参数和边坡几何参数对分项系数的影响特性。通过对土体强度参数变异性这一主导影响因素进行水平划分,给出土体强度参数各变异水平下分项系数推荐值。
1 土质边坡稳定性分析
1.1 边坡稳定可靠度分析基本参数
影响边坡稳定的主要因素有2类:土性参数和边坡几何形状。分项系数的计算分析需要尽量多的考虑各种可能的边坡工况,选取土体黏聚力、内摩擦角的均值和变异系数为强度参数,边坡的坡高和坡率为几何参数,通过调整参数取值,进行工况模拟,研究各参数对分项系数的影响规律。
1.2 功能函数
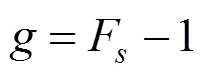
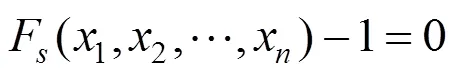

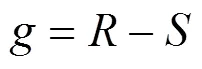
对图1所示的简单土坡,Fellenius法稳定安全系数表达如式(2)。
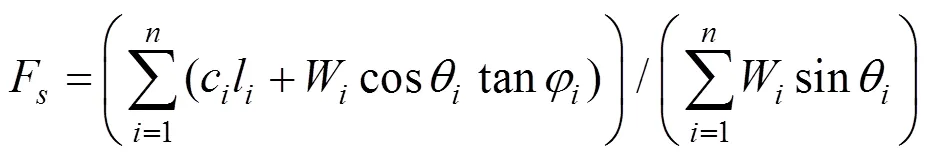

图1 圆弧条分法土条受力分析
Fig. 1 Analysis of soil slice in circular slice method
采用第2种功能函数形式,由式(2)改造后的功能函数为式(3),其中变量1和2为抗力项,为荷载项;式(4)为引入分项系数1,2和的极限状态设计表达式。
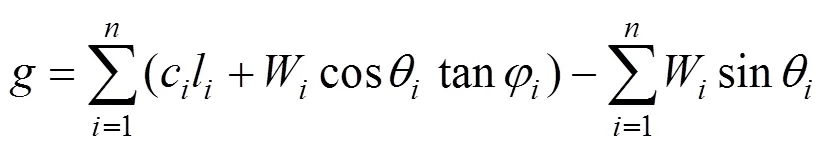
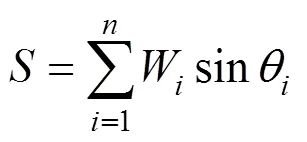

1.3 土工参数变异水平划分
土工参数变异性通过变异系数表征,是标准差和均值的比值,为无量纲系数,用来比较不同指标的变异性,常用表示,如式(5)所示。
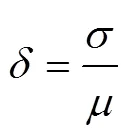
近几十年来,国内外学者对土体强度参数变异性做了大量研究,总结参数变异系数取值范围如表1所列。由于土体容重变对边坡稳定性的影响很小,如文献[10−11]的土体容重变异系数仅为0.01~0.04,Eurocode 7[12]将土体容重分项系数取为1,未考虑变异性。因此,文中计算取土体容重为定值。

表1 抗剪强度参数变异系数汇总
为便于评价岩土参数变异性特征,《地质灾害防治工程勘察规范》(DB 50/143—2003)将岩土参数变异性按等分原则划分为很低、低、中等、高和很高5个水平,参照这一思路且为简化计算,将土体抗剪强度指标变异水平划分为小、中和大3种变异水平,具体分级标准如表2所列。

表2 抗剪强度参数变异水平分级
表2所列土体强度参数变异性三水平划分结果是依据前人对和变异系数间相关性、分布范围研究成果和等分原则提出的,反映了和变异系数分布的一般规律,适用于绝大多数工况。
1.4 目标可靠指标
为获得边坡设计所需要的目标可靠指标,采用校准法[18]对现有规范隐含的可靠度水平进行反演分析。目前既有的铁路路堤边坡是依照《铁路路基设计规范》[19]中的安全系数法进行设计,故按照规范中的技术要求建立边坡断面模型,通过调整基本参数,试算满足稳定性要求的边坡工况,通过可靠度计算获得对应的可靠指标并进行统计分析,即可得到边坡设计目标可靠指标。
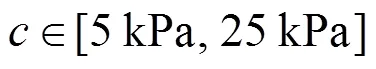
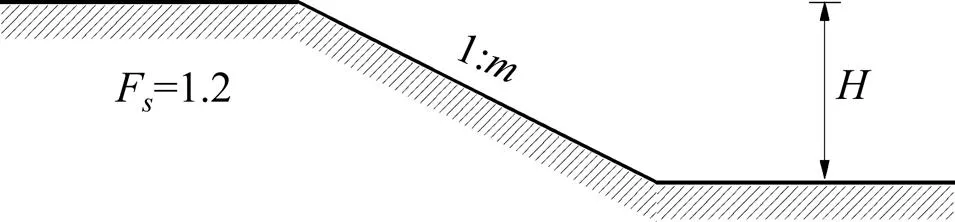
图2 土坡模型尺寸
为保证边坡具有相同的可靠度,安全系数的取值应与土体强度参数的变异性相适应,即设计安全系数取值应随土体强度参数变异性的提高而增大。规范[19]给出的设计安全系数F=1.2在土体强度参数变异水平较小时较为合理,在变异性较大时不可接受[20]。因此在土体参数小变异水平下对设计安全系数进行反演分析,得到的边坡可靠指标才较为真实。假定土体黏聚力和内摩擦角为表(2)小变异,具体计算时,在4~10 m范围以1 m为间隔取值,以0.5 kPa为步长选取,求出对应的,形成{,,}数据组,进行可靠度计算,共得到=166个可靠指标值,绘制频率直方图和累计频率曲线,如图3所示。
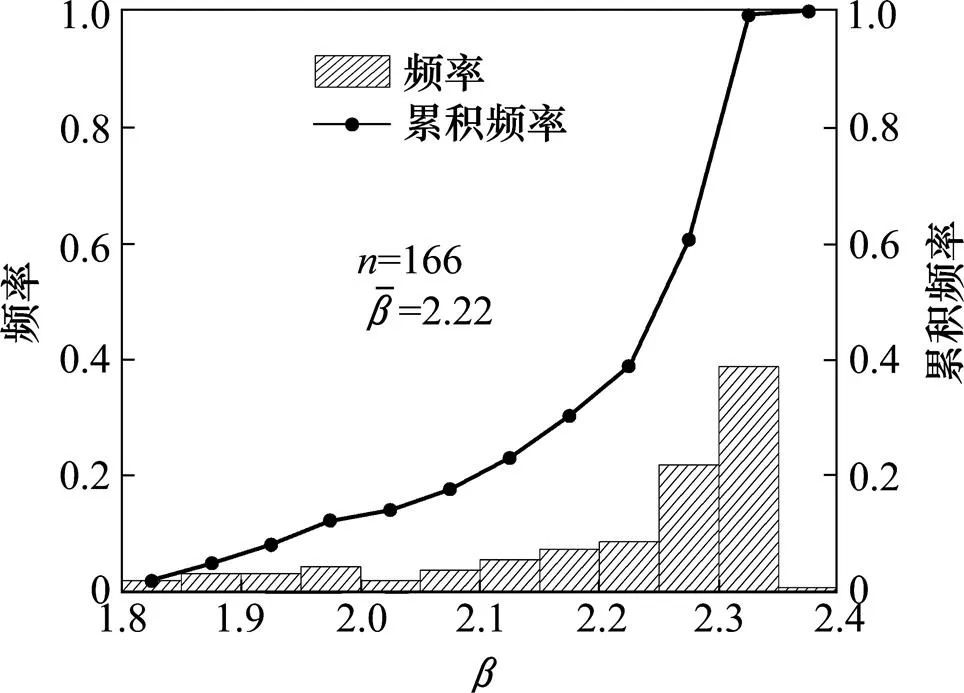
图3 可靠指标频率直方图
由图3可知,在主要分布区间[2.2, 2.35]内频率最高,频率累计曲线斜率最大。目标可靠指标是期望并控制结构物能够达到的安全程度,这个值应能保证绝大部分边坡是足够安全的,因此目标可靠指标应取概率分布中的较高值,又的均值为2.22,0.9分位值为2.33,中位值为2.28,综合考虑取目标可靠指标=2.3。
2 分项系数计算方法
2.1 分项系数定义
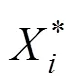
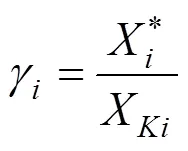
结构工程中材料性能标准值为材料性能概率分布的某一分位值,但这种标准值不适用于岩土工程。因为结构设计验算的是某一截面的强度,破坏模式属于局部破坏。而岩土工程控制设计的并不是某一指定截面上的内力与材料强度的平衡条件,而是由某一范围土体抗力与外力的平衡条件,是该范围内土体沿某一滑动面作用的综合结果,破坏模式属于整体破坏,因此使用土体强度参数均值作为土体性能代表值[22]。Eurocode 7[12]中也推荐采用均值作为岩土工程变量标准值。据此,式(3)中变量1,2和标准值取均值。
2.2 验算点法

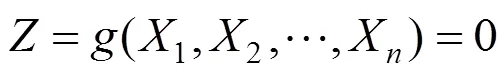

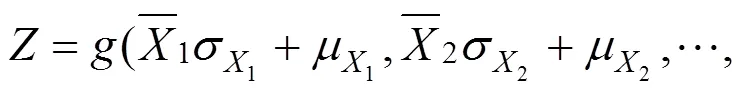
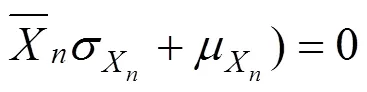

图4 极限状态曲面与设计验算点
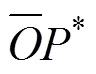
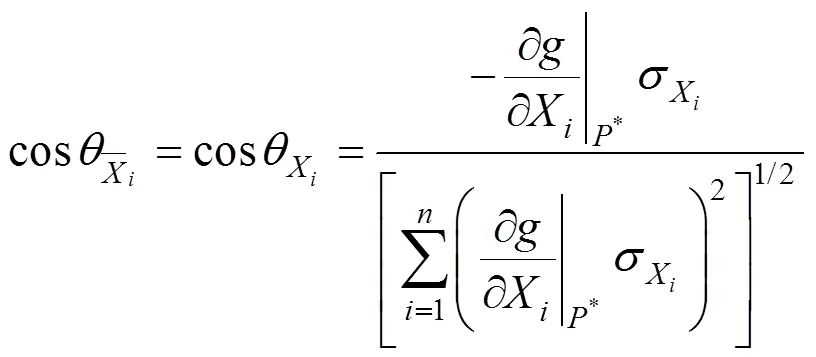
由方向余弦的定义,可知
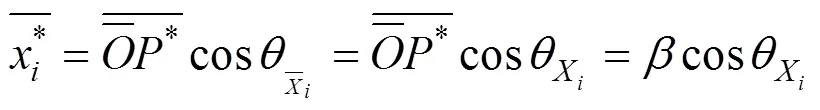
又由(8)式
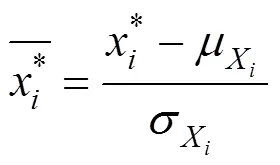
因而

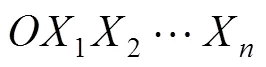

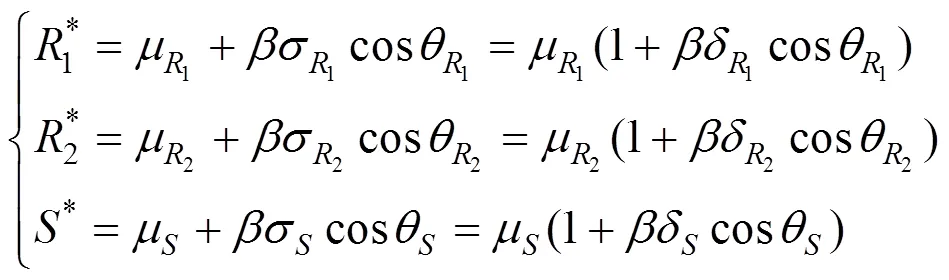
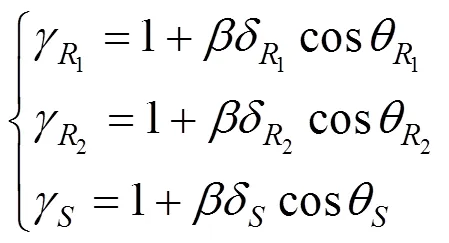

采用Matlab软件编写边坡稳定可靠度计算程序,提取变量1,2和的均值和标准差,代入式(16)求出分项系数。
3 分项系数分析计算
分项系数与边坡极限状态曲面密切相关,而极限状态曲面的形态又是由土体强度参数和边坡几何参数共同决定的,因此每当边坡基本参数发生变化时分项系数也随之变化。分析强度参数和几何参数对分项系数的影响特性,将各参数条件下的分项系数进行统计分析,选出推荐值。

(a) 小变异; (b) 中变异;(c) 大变异
3.1 土体强度参数均值对分项系数的影响
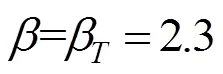
可以看出,随着参数均值的提高(μ降低),2增大而1和都减小,且1变化最大,2次之,变化非常小。另外,在小变异条件下土体强度参数均值对分项系数影响较小,但随着变异水平的提高,分项系数的变化程度也就越来越大,大变异水平下土体强度参数均值就会对分项系数产生较大影响。
3.2 土体强度参数变异性对分项系数的影响
根据分项系数计算结果,作出分项系数随土体强度参数变异水平变化曲线,如图6所示。
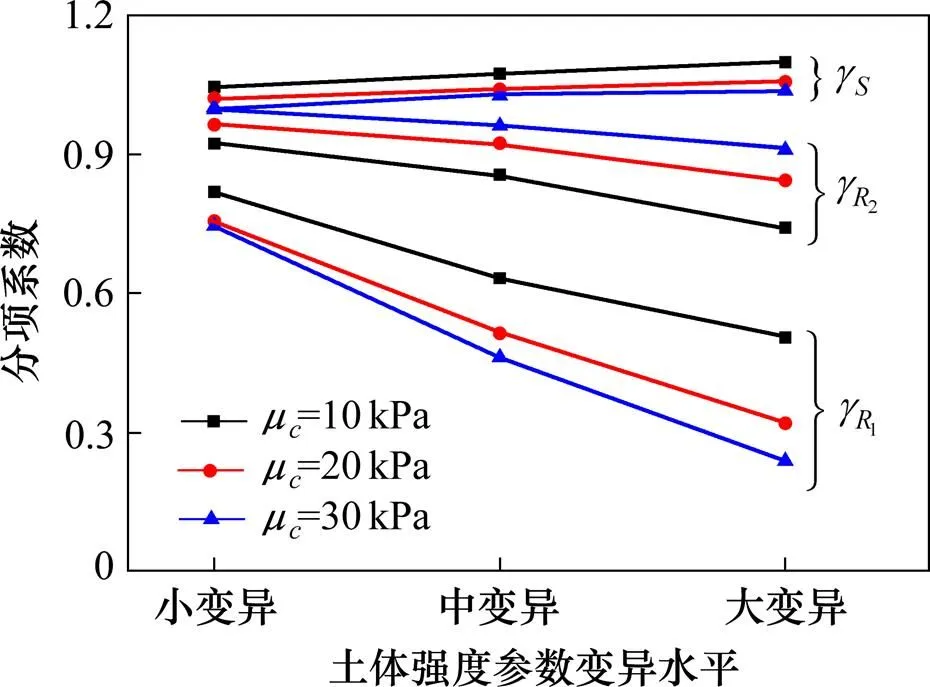
图6 土体强度参数变异水平与分项系数关系
可以看出,相较于强度参数均值,分项系数随参数变异系数变化幅度更大,即强度参数变异系数对分项系数的影响更大。
3.3 边坡坡高对分项系数的影响


图7 边坡坡高与分项系数关系曲线
由图7可知,边坡坡高对分项系数有一定影响,且影响程度与参数变异水平呈正相关,但对分项系数的影响弱于土体强度参数均值和变异系数。
3.4 边坡坡率对分项系数的影响

图8 边坡坡率与分项系数关系曲线
由图8可知,相较于其他影响因素,坡率对分项系数的影响很小。
综上,强度参数变异系数是分项系数的主导影响因素,强度参数均值和边坡坡高也会对分项系数有较大影响,而边坡坡率对分项系数影响微弱。
4 分项系数优选及验证
4.1 优选步骤
以上计算所得分项系数为多种边坡工况下的特定值,进行统计分析以及优选后才能得到分项系数推荐值。优选步骤如下:

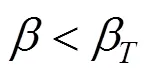

定义各工况下实际可靠指标与目标可靠指标误差为:
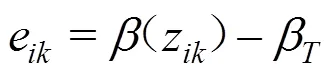
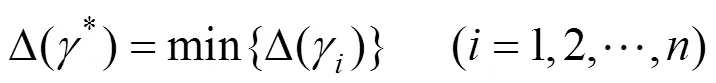
式中:

4.2 拟定分项系数
由于荷载项变异性很小,分布区间窄,为简化计算,直接进行分析选取推荐值。统计所有计算结果并作出频率直方图,如图9所示。
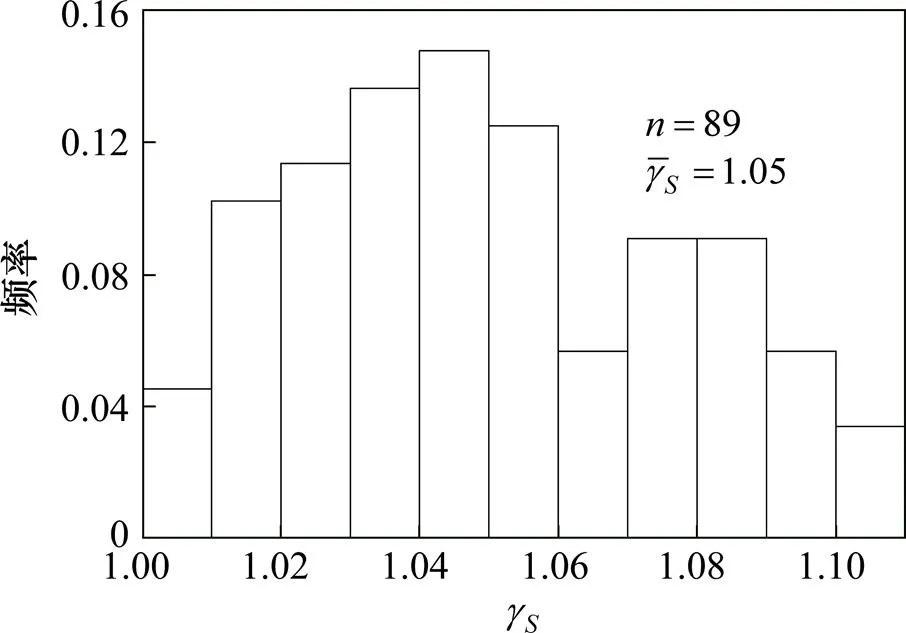
图9 γS频率直方图
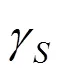
1和2变化范围较大,需要选取拟定值进行标定,求出分项系数推荐值。首先确定1和2分布范围,作出3种变异水平下散点图,如图10 所示。

图10 γR1与γR2分布散点图
由图10可知,土体强度参数变异水平越高,散点离散性越大且具有很强的负相关性。确定1与2特征值并选取拟定制,以中变异为例,1与2的均值、最小值和拟定值如表3所示。
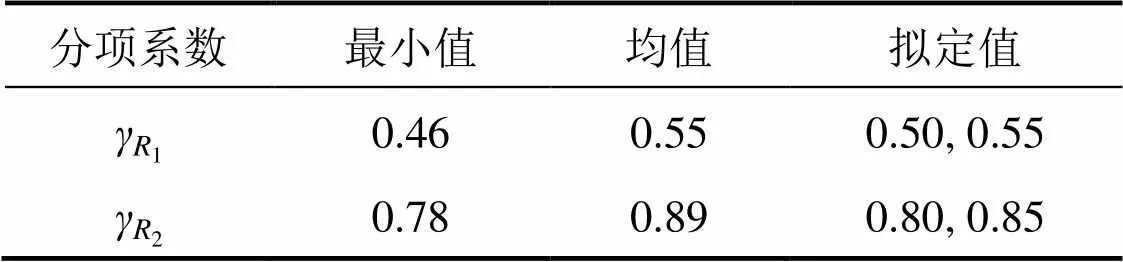
表3 γR1和γR2特征值与拟定值
将1,2和进行组合得到(1,2,)拟定值为(0.50, 0.85, 1.06),(0.50, 0.90, 1.06),(0.55, 0.85, 1.06)和(0.55, 0.90, 1.06)。
4.3 标定分项系数
以中变异为例进行分项系数标定,建立图2所示边坡模型,坡高=8 m,坡率1:=1:1.5,初始强度参数均值=10 kPa,μ=20°。土体强度参数变异性是分项系数主导影响因素,因此选取黏聚力和内摩擦角变异系数和δ为验算控制参数,通过改变或δ来进行工况组合,取0.15,0.2和0.25;δ取0.075,0.10和0.125。当仅改变时,控制μ不变,求出满足式(17)的μ;同样的,当仅改变δ时,控制不变,求出满足式(17)的μ。计算每个工况组合的实际可靠指标并按式(20)计算误差平方和。计算结果如表4所示。
由表4可知,分项系数拟定值(0.55, 0.90, 1.06)在不同工况的实际可靠指标与目标可靠指标误差平方和最小,并且误差均大于−0.25,因此取(0.55, 0.90, 1.06)为土体强度参数中变异分项系数推荐值。同样的,求出土体强度参数小变异和大变异的推荐值,如表5所示。
4.4 与现行规范比较
为了便于与《铁路路基极限状态法设计暂行规范》[9]中给出的分项系数进行对比,将设计表达式与分项系数改写为表6中的形式。
可以看出,规范推荐值与文中小变异推荐值总体上对于抗力折减及荷载放大的程度相同,但当土体强度参数为中变异和大变异水平时对1项变异性考虑不足,因此规范推荐值基本仅适用于土体强度参数小变异的边坡设计,为使土体变异性不同的边坡具有一致可靠度须采用与土体强度参数变异水平相适应的分项系数进行设计。
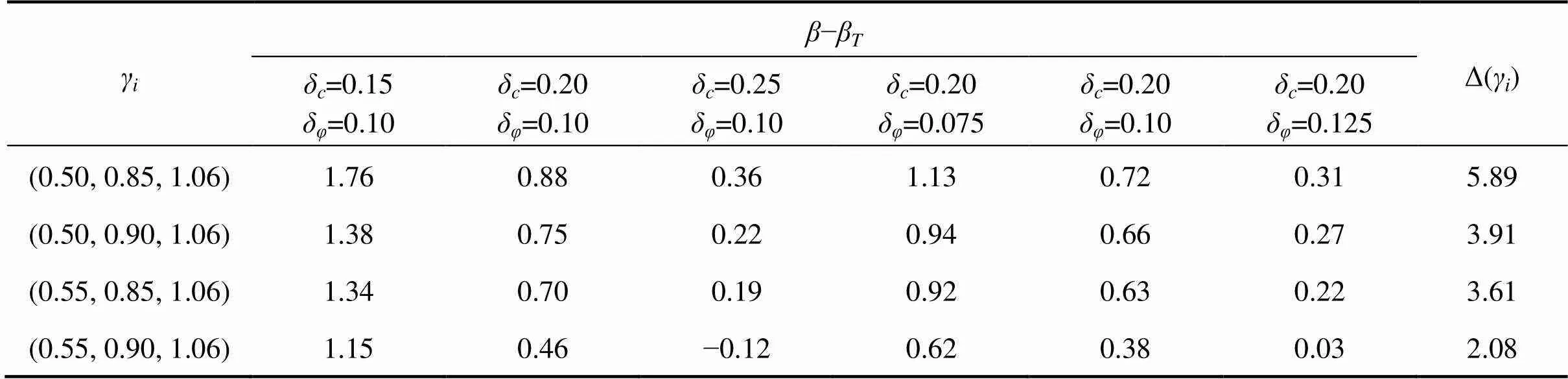
表4 分项系数标定结果

表5 分项系数推荐值
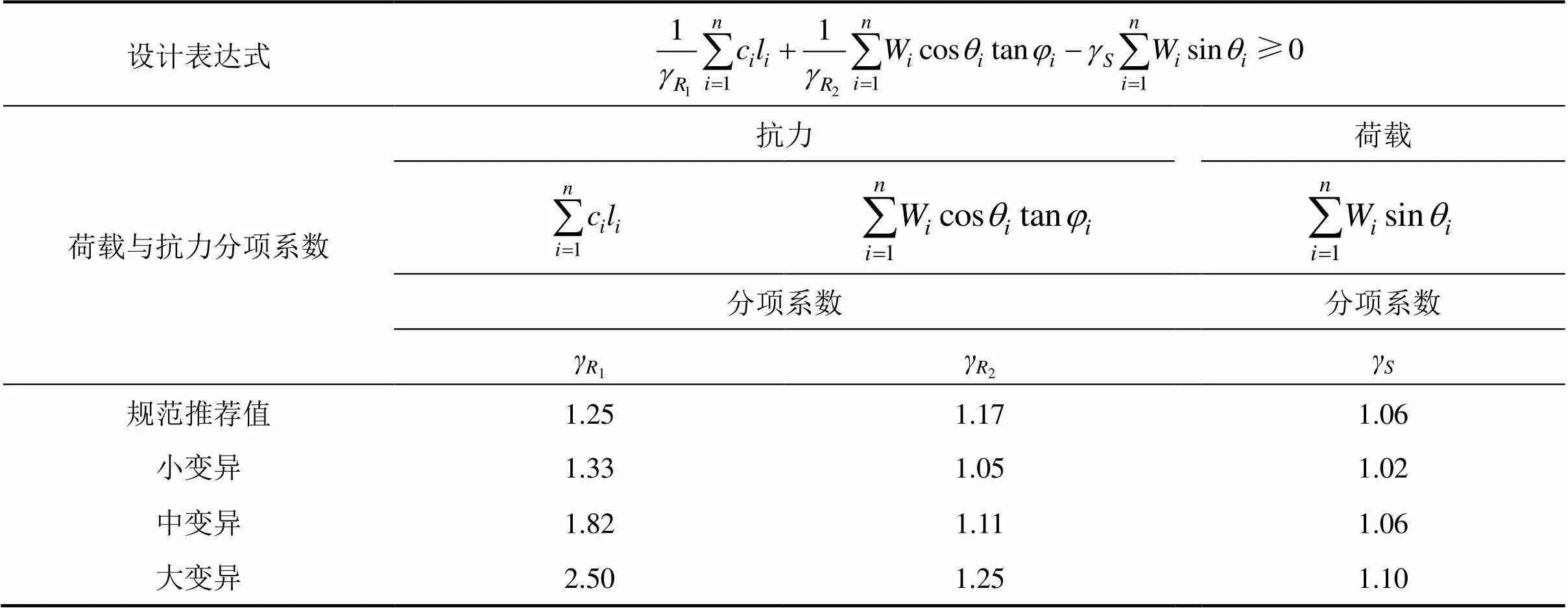
表6 分项系数推荐值
此外,同铁路暂行规范比较,表6中黏聚力分项系数整体偏大,但摩擦角分项系数整体偏小,这是因为规范中取值与表2的小变异水平相接近,δ取值与表2的中、大变异水平相接近。
5 结论
1) 以现有规范典型边坡几何尺寸和安全系数为依据,考虑实际工程导向安全的设计理念,校准确定了铁路路堤边坡目标可靠指标为2.3。
2) 土体强度参数变异性是影响边坡极限状态设计分项系数取值的主导因素,其次为土体强度参数均值和坡高,坡率对分项系数影响微弱。
3) 为使不同变异性的土质边坡具有一致可靠度,须采用与土体强度参数变异水平相适应的分项系数进行设计,强度参数小,中和大变异水平对应的铁路路堤边坡极限状态设计分项系数(1,2;γ)推荐值分别为(0.75, 0.95; 1.02),(0.55, 0.90; 1.06)和(0.40, 0.80; 1.10)。
[1] Phoon K K, Kulhawy F H. Characterization of geotechnical variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 612−624.
[2] Akbas S O, Kulhawy F H. Characterization and estimation of geotechnical variability in ankara clay: a case history[J]. Geotechnical and Geological Engineering, 2010, 28(5): 619−631.
[3] Sina J, Richard J B. Simplified probabilistic slope stability design charts for cohesive and cohesive-frictional soils[J]. Journal of Canadian Geotechnical, 2014, (51): 1033−1045.
[4] WU T H, Kraft L M. Safety analysis of slopes[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(2): 609−630.
[5] 郭重凤. 国际工程中外设计差异分析及应对策略研究[J]. 铁道工程, 2017, 34(7): 1−4. GUO Chongfeng. Design difference analysis and coping strategies for international project[J]. Journal of Railway Engineering Society, 2017, 34(7): 1−4.
[6] 王仲锦, 吴敏敏, 程爱君, 等. 铁路路堤边坡的可靠度设计方法研究[J]. 铁道工程学报, 2013(3): 24−27. WANG Zhongjin, WU Minmin, CHENG Aijun, et al. Study on design method for slope reliability of railway embankment[J]. Journal of Railway Engineering Society, 2013(3): 24−27.
[7] 张宁, 李旭, 储昭飞, 等. 关于土坡稳定分析中的分项系数取值讨论[J]. 岩土工程学报, 2015, 38(9): 1695− 1704. ZHANG Ning, LI Xu, CHU Zhaofei, et al. Discussion on the optimum partial factor values in the stability analysis of soil slope[J]. Chinese Journal of Geotechnical Engineering, 2015, 38(9): 1695−1704.
[8] 吴兴正, 蒋良潍, 罗强, 等. 路堤边坡稳定可靠度计算中的模型不确定性分析[J]. 岩土力学, 2015, 36(增2): 665−672. WU Xingzheng, JIANG Liangwei, LUO Qiang, et al. Analysis of model uncertainty for stability reliability of embankment slope[J]. Rock and Soil Mechanics, 2008, 36(Suppl 2): 665−672.
[9] Q/CR 9127—2015, 铁路路基极限状态法设计暂行规范[S]. Q/CR 9127—2015, Interim code for limit state design of railway earth structure[S].
[10] 张继周, 缪林昌, 陈俊波. 苏中腹地湖相软土土性参数变异性统计描述[J]. 岩土力学, 2010, 31(2): 471−477. ZHANG Jizhou, MIAO Linchang, CHEN Junbo. Statistical characterization of variability of lacustrine soft soil in central region of Jiangsu province[J]. Rock and Soil Mechanics, 2010, 31(2): 471−477.
[11] Roh Gwangha, HONG H P. Calibration of information-sensitive partial factors for assessing earth slopes[J].Journal of Geoengineering, 2009, 4(3): 95−96.
[12] CEN (European Committee for Standardization). EN 1997-1, Eurocode7: Geotechnical Design--Part 1[S]. Brussels, 2004.
[13] 高大钊. 地基土力学性质指标的可靠性分析与取值[J]. 同济大学学报(自然科学版), 1985, 25(4): 59−68. GAO Dazhao. The reliability of the mechanics properties of foundation soil index analysis and value[J]. Journal of Tongji University (Natural Science), 1985, 25(4): 59−68.
[14] 李小勇. 土工参数空间概率特性及软黏土地基固结概率分析[D]. 杭州: 浙江大学, 2001. LI Xiaoyong. Spatial probabilistic characteristics of geotechnical parameters and probability analysis of consolidation of soft clay ground[D]. Hangzhou: Zhejiang University, 2001.
[15] 聂士诚. 土质边坡稳定的可靠度分析及其土性参数的敏感性研究[D]. 长沙: 中南大学, 2002. NIE Shicheng. Reliability analysis of slope stability and research on sensitivity of soil parameters[D]. Changsha: Central South University, 2002.
[16] 陈善攀. 土质边坡稳定可靠度分析遗传算法方法及程序设计[D]. 长沙: 中南大学, 2008. CHEN Shanpan. Genetic algorithm method and program design for reliability analysis of soil slope stability[D]. Changsha: Central South University, 2008.
[17] EL-RAMLY H. Probabilistic analyses of landslide hazards and risks: bridging theory and practice[D]. Alta: University of Alberta, Edmonton, 2001.
[18] GB 50216—94, 铁路工程结构可靠度设计统一标准[S]. GB 50216—94, Unified design standard for reliability of railway engineering structures[S].
[19] TB10001—2015, 铁路路基设计规范[S]. TB10001—2015, Code for design on subgrade of railway [S].
[20] 骆飞, 罗强, 蒋良潍, 等. 土体抗剪强度指标变异水平对边坡稳定安全系数取值的影响[J]. 土木建筑与环境工程, 2015, 37(4): 77−83. LUO Fei, LUO Qiang, JIANG Liangwei, et al. Influence of variation levels of soil strength indexes on the value of slope stability factor[J]. Journal of Civil, Architectural & Environmental Engineering, 2015, 37(4): 71−83.
[21] GB 50199—2013, 水利水电工程结构可靠性设计统一标准[S]. GB 50199—2013, Unified design standard for reliability of hydraulic engineering structures[S].
[22] 张文生, 罗强, 蒋良潍, 等. 边坡稳定分析中岩土参数置信水平取值探讨[J]. 铁道科学与工程, 2017, 14(4): 697−704. ZHANG Wensheng, LUO Qiang, JIANG Liangwei, et al. Value of confidence level for geotechnical parameters in slope stability analysis[J]. Journal of Railway Science and Engineering, 2017, 14(4): 697−704.
Discussion on the value of partial factors considering variation level of geotechnical parameter in slope stability analysis
LI Ang1, 2, LUO Qiang1, 2, ZHANG Wensheng1, 2, JIANG Liangwei1, 2, ZHANG Liang1, 2
(1. School of Civil Engineering Southwest Jiaotong University, Chengdu 610031, China; 2. MOE Key Laboratory of High speed Railway Engineering Southwest Jiaotong University, Chengdu 610031, China)
Large variation of geotechnical property result in large discrete of engineering reliability index, reliability index of engineering can not achieve our goals by single partial factors, The variability of soil strength parameter was divided into three grades: small, medium and large, a series of simple slope models with a variety of geometric and intensity parameters was constructed based on the calibration method and carrying out stable reliability calculation, and determine the target reliability index is 2.3. Calculating the partial factors by design point method, the influence of soil strength parameters and slope geometric parameters on the partial factor was discussed, and the recommended values of the partial factors under the three variation levels were calculated by the design point method. Study shows that the coefficient of variation of soil strength parameters is the dominant factor for the partial factors, mean value of soil strength parameters and slope height also have a certain impact on the partial factors, the effect of slope rate on partial factors is small; In order to make the slope with different variation of strength parameters to achieve consistent reliability, value principle is proposed partial factors should be adapted to the level of parameters variation, and the recommended values of the resistance term and the load term of the partial factors with small, medium, and large parameter variation level are (0.75, 0.95, 1.02), (0.55, 0.90, 1.06), (0.40, 0.80, 1.10).
stability analysis of slope; variation level of parameter; partial factor; target reliability index; design point method
10.19713/j.cnki.43−1423/u.2019.02.009
U213.1+3
A
1672 − 7029(2019)02 − 0341 − 10
2018−01−22
国家重点基础研究发展计划(973计划)项目(2013CB036204)
罗强(1963−),男,四川宜川人,教授,博士,从事铁路路基基床结构设计研究;E−mail:lqrock@home.swjtu.edu.cn
(编辑 涂鹏)
