基于收益管理的高铁动态定价方法

徐彦



基于收益管理的高铁动态定价方法

徐彦

(中国铁路总公司 客运部，北京 100844)

以高速铁路市场化定价为背景，提出高速铁路动态定价模型。根据列车停站方案的差异，以列车旅行时间进行列车分级；通过分析高铁沿线各点对之间的历史客流出行信息，从旅客出行的价格敏感性和时间敏感性角度出发对旅客进行分类，并根据历史售票数据得出不同类型旅客所占比例；在此基础上，以客票总收益最大化为目标，考虑票价上下限、列车能力和票价不到倒等约束，建立基于收益管理的高速铁路动态票价优化模型，并根据模型特征设计启发式求解方法。最后以京沪高铁为例，利用所提出的方法进行优化计算和分析，证明在不增加运力的前提下，考虑收益管理的高铁动态定价方法，可以有效提高客票收益。

高速铁路；收益管理；动态定价；优化模型

我国拥有全世界最大规模的高铁运营网络，但高铁客票票价政策一直未能充分考虑市场需求特征、运输企业收益等实际情况，缺乏科学且灵活的市场化调整机制。在国家大力推行价格市场化改革的大背景下，探索我国高铁可行的优化定价策略，已成为我国高铁未来发展中亟待解决的关键问题。收益管理定价，又称动态定价，是指在适当的时间，以适当的价格向适当的客户销售适当的产品，以最大化企业的收益。面向收益管理制定产品动态价格的机制，已经在航空、酒店等领域得到广泛应用，并取得良好增收效果。在航空领域，YOU[1]研究了考虑不同席位等级的多航段航空动态定价问题；LUO等[2]提出了基于市场竞争的航班收益管理动态定价模型；DAN[3]研究了基于相同起终点条件下，可替代航班的收益管理定价问题；Otero等[4]研究了考虑旅客支付意愿，不同席位等级的航空随机动态定价问题。铁路运输相对航空运输要复杂很多，因为在同一个航班超过2个航段的情况极为少见，但是铁路客运是一种多停站的运输组织方式，其能够为众多点对之间的旅客提供服务，加之列车席位众多，导致形成庞大的状态空间，为问题的求解带来了极大的困难。Armstrong等[5]对铁路客运与货运收益管理模型与方法进行了回顾；Vuuren[6]尝试建立最优定价经济理论与铁路价格需求弹性及边际成本之间的内在联系；Piening等[7]基于提出了影响旅客忠诚度的影响因素；LIN[8]研究了基于不确定需求的动态定价问题。史峰等[9]研究了我国铁路动态票价最优策略和实用性问题，并给出递推公式；陈建华等[10]探讨了双层规划模型在制定铁路票价的应用；李博等[11]研究了同一OD间两列平行车次的动态定价问题；杨宇航等[12]分析了高铁收入与票价之间的关系，提出面向收益优化的票价区间；刘帆洨等[13]利用半马尔科夫决策提出单次决策收益期望模型，并推广得到单列车票额预售控制决策模型；朱颖婷[14]研究了铁路客运票价策略与收益优化方法；方磊[15]建立了高铁坐席存量与差别定价联合决策模型。由于铁路动态票价存在席位状态随服务点对数的增加呈现指数增长的规律，导致既有的铁路动态定价问题大多还是基于单点对开展研究。为此，本文在进行旅客分类和列车分级的基础上，基于“基准票价+浮动票价”的高铁票价机制，利用数学优化模型研究基于席位管理的高铁动态票价确定方法，并建立以旅客广义出行费用最小的客流加载仿真模型，为高速铁路多区段的动态定价方案提供参考。

1 变量定义与假设

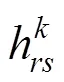
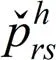
其中：为规定的最低票价折扣率。

基于席位管理的理念，结合日本高铁的票价模式，即“基准票价＋浮动票价”的构成形式，构造执行票价的确定方法如下：

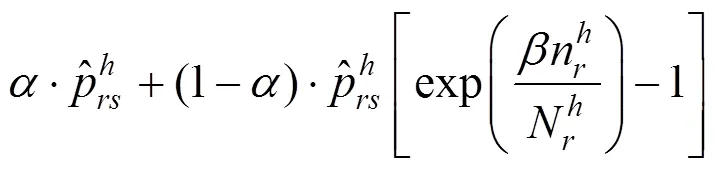
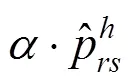
由此，实际执行票价是由根据构造函数所得的执行票价水平，与上限票价中的较小值确定，即：

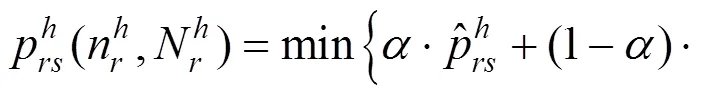
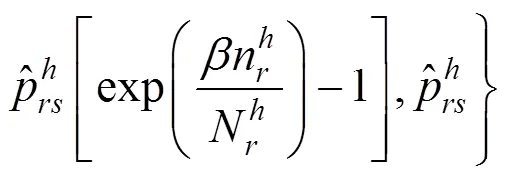
点对(,)之间的实际客流，会受各列车执行票价水平的影响，且不超过列车运行能力()。

为便于建立优化模型，作如下合理假设：

1) 铁路的售票优先满足长途及临近始发站端的购票需求；

2) 铁路售票为单张发售；

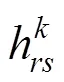
2 高铁动态定价模型

本文提出的模型为考虑高速铁路线路中包含多停站，具有相同起终点的有多趟非平行列车的动态定价模型。

2.1 列车分级

结合旅客的出行分布规律与出行需求特征，铁路总公司提供不同等级的运输服务产品供旅客自主选择，以满足不同旅客的出行需求。

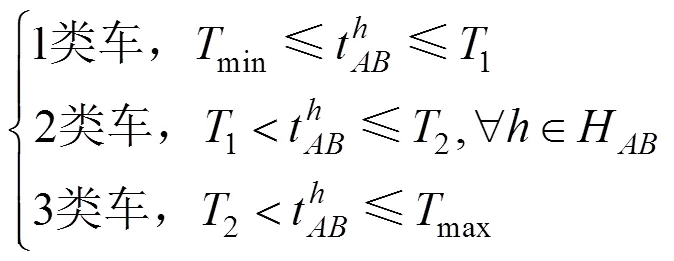
其中：和分别为该线路的起点与终点；1和2为列车分类的临界旅行时间，且1＜2；min和max为所有列车全程旅行时间的最值。

对3类列车划分的主要依据，是列车面向的服务群体不同而提供差别化运输产品，主要以列车的停站方案与行程时间为标准对其进行划分。1类车的停站不含小站，只为大站之间的旅客提供快速运输服务，其旅行时间相对较短；3类车的停站包含小站，能为小站到发的旅客提供服务，其旅行时间相对也较长；2类车则介于两者之间。

2.2 旅客分类

不同旅客群体具有不同的出行需求特征和选择偏好，根据旅客对出行时间敏感性和价格敏感性的不同，将旅客分为商务型、休闲型和中间型3类。

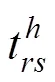
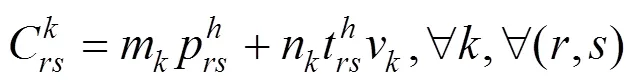
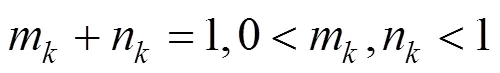
其中：m和n分别为旅客的价格敏感系数和时间敏感系数。

计算旅客的最小广义出行费用：

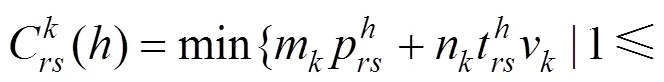
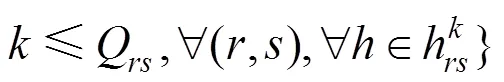
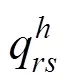
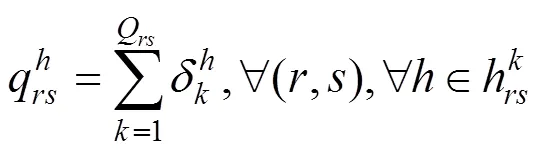
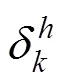
2.3 优化模型

根据前面的分析，可以建立面向收益管理的高铁动态定价模型如下：

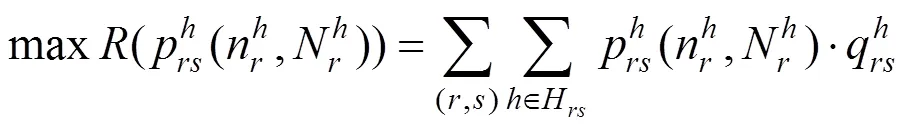
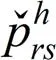
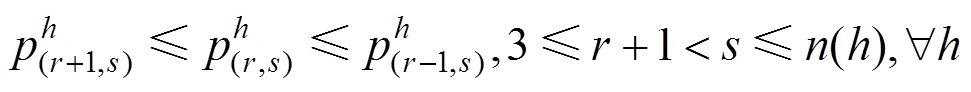
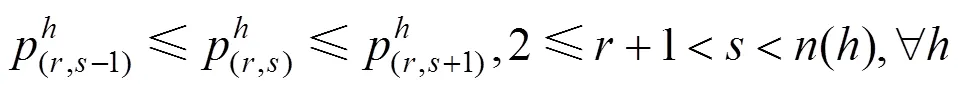
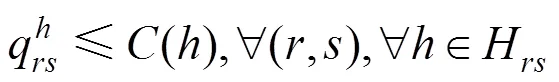
式(10)计算模型总收益，约束条件(11)表示票价上下限约束，约束条件(12)、(13)表示票价不倒挂约束，约束条件(14)表示每趟动车组所载运的客流数量，不应超过该列车的实际运输能力(席位数)。

3 求解算法

根据高速铁路动态定价问题的特点，并结合所提出的优化模型的特征，设计了启发式求解算法。算法的具体步骤如下。

Step 1：选定优化线路，并根据该线路历史售票数据，获取该线路各区间客流量Q及列车开行方案等信息；

Step 2：列车分级，旅客分类，并设置模型参数：站点数、列车能力()、最低折扣率、票价调节参数、价格敏感系数m、时间敏感系数n以及平均时间价值v；

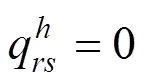
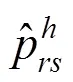
Step 6：若≤Q，执行Step 7，否则执行Step 9；

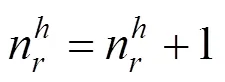
Step 10：根据式(10)计算模型总收益。

4 算例分析

4.1 数据准备

本文以京沪高铁为研究对象，运用所提出动态定价模型进行计算与分析。不失一般性，这里仅考虑京沪高铁上行方向的票价设置问题。

根据京沪高铁2016−08−01~2017−07−31之间的全部历史售票数据，上海虹桥始发至北京南终到的高铁列车共36个车次，累计年发送旅客量为：商务坐席83 855人次、一等坐席362 009人次和二等坐席2 689 305人次，日均区段客流也可通过客票数据获取，且日均票款收入为15 808 468元，二等座全程票价为553元。对于列车分级，取1=5 h，2=5 h 50 min，由式(5)对京沪线上行所有36趟列车分级如下：1) 1类车：G6，G8，G2，G10，G12，G4，G14，G16，G18和G22，共10个车次；2) 2类车：G104，G120，G116，G124，G134，G146，G170，G150，G154和G158，共10个车次；3) 3类车：G102，G106，G108，G110，G112，G114，G122，G126，G130，G132，G412，G138，G140，G142，G148和G152，共16个车次。

对模型中的各项参数标定如下：对京沪间所有列车开行方案的统计分析可知，京沪间所有列车的全程最短旅行时间min=4 h 18 min(G22)，最长旅行时间min=6 h 20 min(G412)；1，2和3类车次对应的最低折扣率分别为0.80，0.77和0.75；根据历史售票数据统计分析，不同类型旅客占比如下：商务型旅客：0.027，中间型旅客：0.115，休闲型旅客：0.858；票价调节参数：反应执行票价随剩余席位数变动而变化的敏感程度，通过对多个候选数值进行效果比选，本算例拟取=4；不同类型旅客的价格敏感系数、时间敏感系数及平均时间价值参数借鉴文献[12]，具体取值如表1所示。另外，假设京沪线上所有列车均采用CRH380BL型动车组，且所有列车能力()=1 015人。

表1 不同类型旅客各参数取值

4.2 结果分析

根据上述动态定价模型与选取的参数，计算铁路客票总收入为17 311 338元，较原先总收入 15 808 468元增加1 502 870元，增幅为9.51%。

对京沪线各点对(,)之间出行需求按照不同旅客类型进行客流加载仿真，所得到京沪线不同站点之间所有车次到北京南站的最优票价如图1所示。从图中可以发现，沿线各站点至终点站的票价依旅行距离整体呈现上升趋势；结合式(3)可知，同一点对票价浮动的极差反应了出发站点出行客流规模的大小。

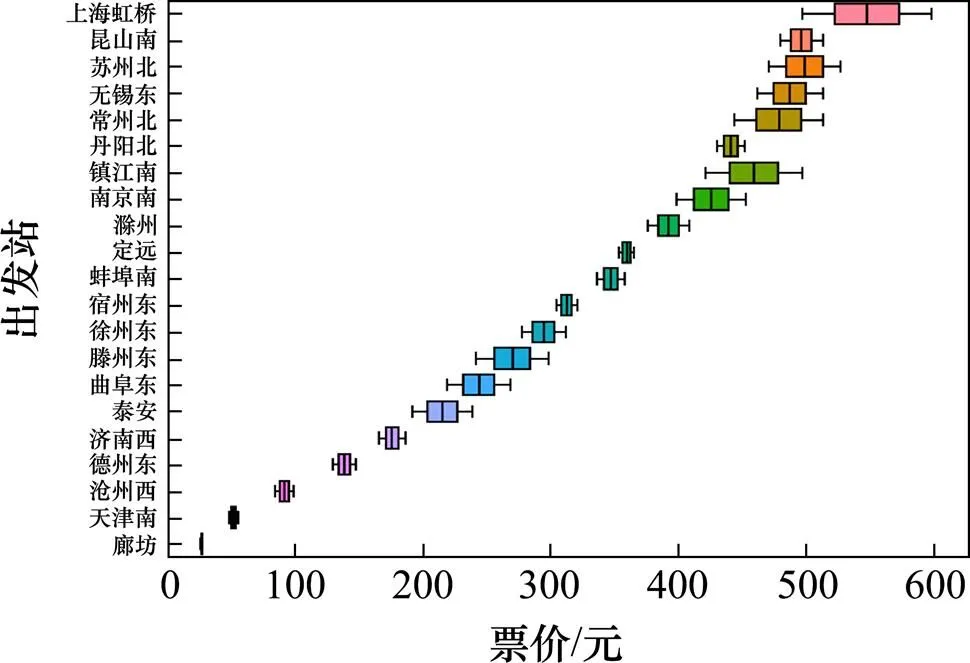
图1 各站点至北京南站票价浮动范围

图2统计了各车次客流在各站点下车人数，由图2可知：南京南和济南西为2个主要的中间下客站点，显然，这部分下车旅客的席位在售票过程中发生了裂解，如何针对这2个站的后续上车客流的出行需求，使后续客流衔接并利用好这部分裂解席位将是改善整体收益的重要环节。

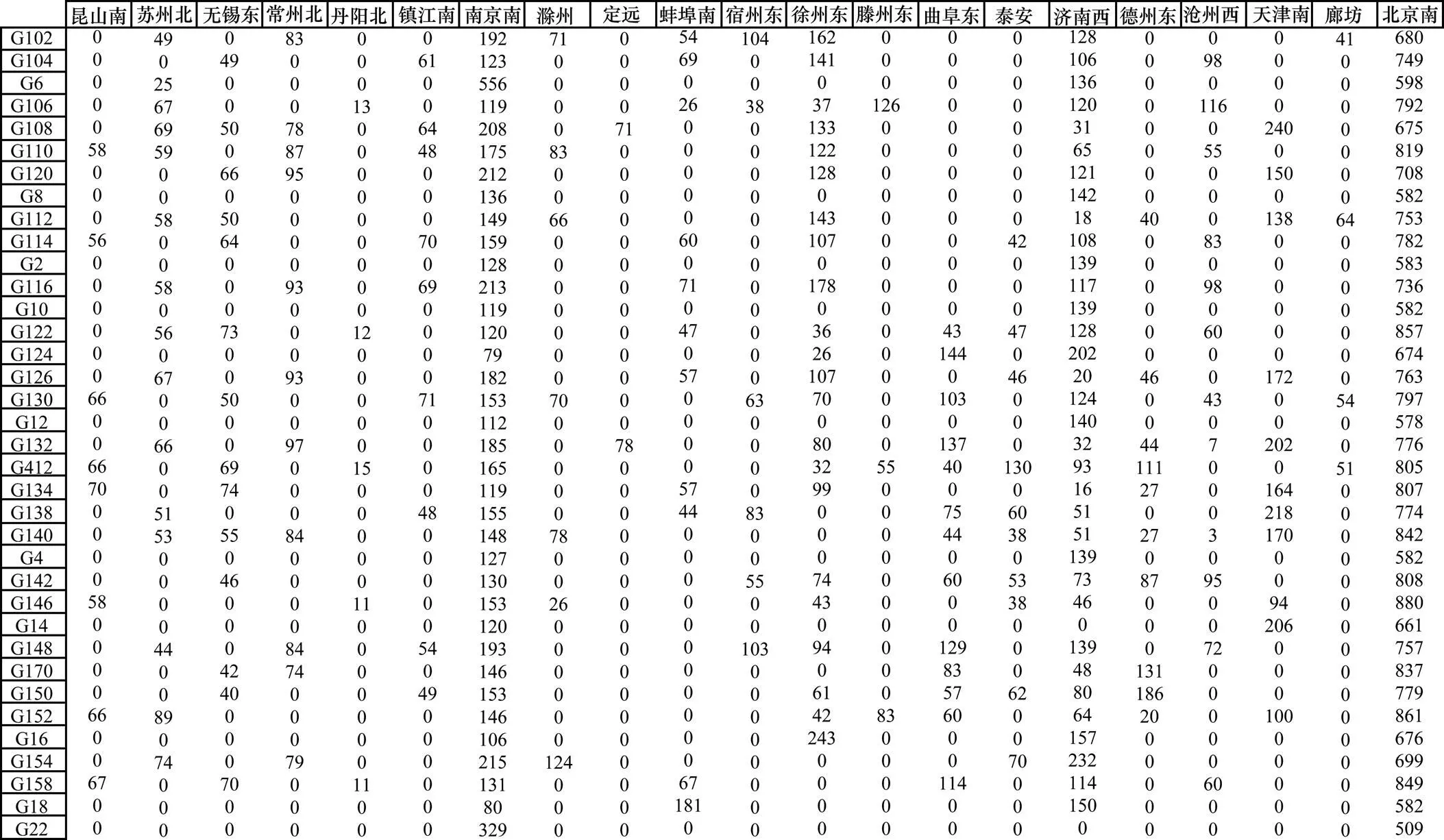
图2 各车次各站到达旅客数量

将计算求取的动态票价与公布票价进行对比，以执行定价与公布票价的比值(即折扣率)为纵轴，以已发售车票数与最大可售车票数的比值(即售票率)为横轴，折扣率随售票率的变化关系如图3所示。

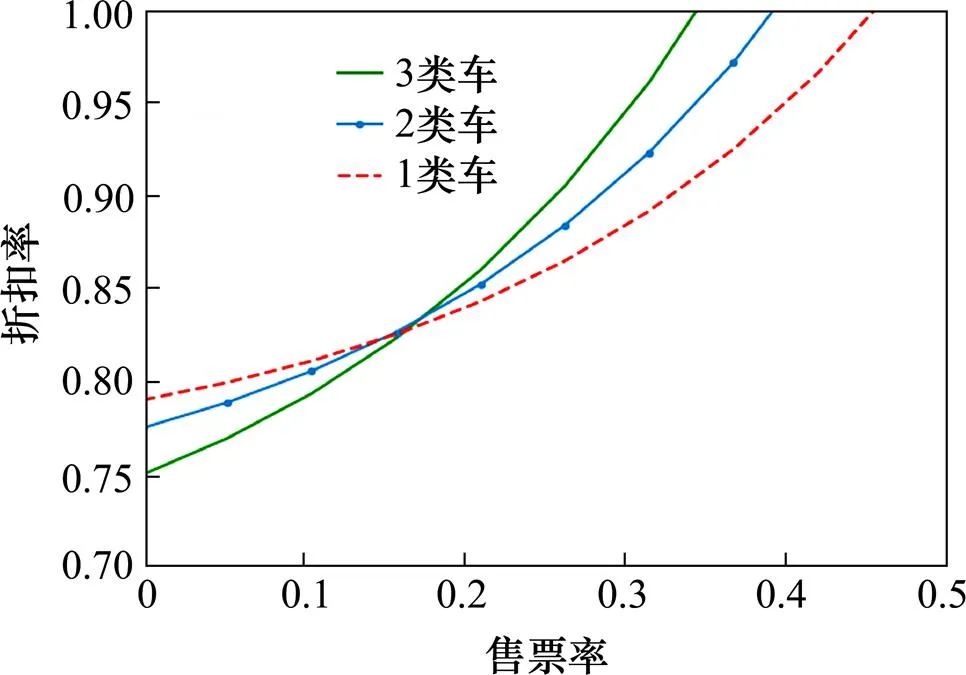
图3 不同列车类型折扣率-售票率变化

从图3可知，当售票率小于列车能力的17.3%时，列车执行票价水平关系为：1类车＞2类车＞3类车；否则，列车执行票价水平关系为：3类车＞2类车＞1类车。执行票价水平排序发生变化的原因在于：一方面，3类车可以满足小站到发的出行需求，这部分旅客只能选择特定车次出行，可选范围小，不同车次之间的可替代性弱，因此可以提升票价水平从而提升收益；另一方面，若3类车的票价水平在3类列车中一直处于最低水平，则大站到发的旅客也会聚集到3类车上，导致3类车在小站停车时没有乘降需求；同时也会导致1类车与2类车客座率低下，造成运力浪费；而真正有小站到发需求的旅客却因3类车运输能力不足，购票需求无法得到满足，造成客流损失。综上所述，3类列车的票价水平排序发生变化是合理的，也是必要的。

在上述模型算例中，还可以通过调整不同分级车次的最低折扣率、票价调节参数以及列车能力()(如调整列车长短编组或者更换动车组车型等)等参数，或者修改列车开行方案等方法，得到不同的收益效果。

5 结论

1) 基于席位管理理念，提出了高速铁路列车执行票价的构造函数，明确了不同列车车次的涨价时机，确定了不同价位车票的最大售票量等动态定价中的关键问题。

2) 以京沪高铁为对象，根据最小广义费用进行客流加载仿真，在此基础上进行计算分析，验证了模型的有效性，证明了动态定价方法确实可以在不增加运力的前提下，增加运输企业的客票总收益。

3) 在动态定价中，票价的制定取决于市场的供需关系。由于铁路票价需满足不倒挂约束，若在列车停站方案制定过程中，将某个紧邻大站的前方小站设立停站，则大站票价的上涨空间将严重受到抑制，且抑制效果会一直沿着停站方案向后方所有站点传递。

[1] YOU P S. Dynamic pricing in airline seat management for flights with multiple flight legs[J]. Transportation Science, 1999, 33(2): 192−206.

[2] LUO L, PENG J H. Dynamic Pricing model for airline revenue management under competition[J]. Systems Engineering-Theory & Practice, 2007, 27(11): 15−25.

[3] DAN Z. Pricing substitutable flights in airline revenue management[J]. European Journal of Operational Research, 2009, 197(3): 848−861.

[4] Otero D F, Akhavan-Tabatabaei R. A stochastic dynamic pricing model for the multiclass problems in the airline industry[J]. European Journal of Operational Research, 2015, 242(1): 188−200.

[5] Armstrong A, Meissner J. Railway revenue management: overview and models (Operations Research)[R]. Lancaster University, 2010: 9−18.

[6] Vuuren D V. Optimal pricing in railway passenger transport: theory and practice in the netherlands[J]. Transport Policy, 2002, 9(2): 95−106.

[7] Piening J, Ehrmann T, Meiseberg B. Competing risks for train tickets–An empirical investigation of customer behavior and performance in the railway industry[J]. Transportation Research Part E Logistics & Transportation Review, 2013, 51(3): 1−16.

[8] LIN K Y. Dynamic pricing with real-time demand learning[J]. European Journal of Operational Research, 2006, 174(1): 522−538.

[9] 史峰, 郑国华, 谷强. 铁路客票最优动态票价理论研究[J]. 铁道学报, 2002, 24(1): 1−4. SHI Feng, ZHENG Guohua, GU Qiang. Research on the optimal dynamic fare theory of railway passenger tickets[J]. Journal of the China Railway Society, 2002, 24(1): 1−4.

[10] 陈建华, 高自友. 基于双层规划模型的铁路票价制定优化策略[J]. 北方交通大学学报(社会科学版), 2003, 2(3): 38−41. CHEN Jianhua, GAO Ziyou. Optimization strategy of railway ticket pricing based on bi-level programming model[J]. Journal of Northern Jiaotong University (Social Science Edition), 2003, 2(3): 38−41.

[11] 李博, 赵鹏, 李云峰, 等. 基于旅客分类的高速铁路平行车次动态定价研究[J]. 铁道学报, 2017(9): 10−16. LI Bo, ZHAO Peng, LI Yunfeng, et al. Dynamic pricing of parallel trains for high-speed railway based on passenger classification[J]. Journal of the China Railway Society, 2017(9): 10−16.

[12] 杨宇航, 张琦. 京沪高速铁路票价调整与优化策略研究[J]. 铁道科学与工程学报, 2017, 14(10): 2043−2049. YANG Yuhang, ZHANG Qi. Research on ticket adjustment and optimization strategy of Beijing-Shanghai high speed railway[J]. Journal of Railway Science and Engineering, 2017, 14(10): 2043−2049.

[13] 刘帆洨, 彭其渊, 梁宏斌, 等. 铁路客运票额预售控制决策模型研究[J]. 铁道学报, 2018(1): 17−23. LIU Fanzhen, PENG Qiyuan, LIANG Hongbin, et al. Research on decision model of pre-sale control of railway passenger tickets[J]. Journal of the China Railway Society, 2018(1): 17−23.

[14] 朱颖婷. 铁路客运票价策略与收益优化研究[D]. 北京: 中国铁道科学研究院, 2015. ZHU Yingting. Research on railway passenger transport price strategy and profit optimization[D]. Beijing: China Academy of Railway Sciences, 2015.

[15] 方磊. 基于收益管理的高铁票价和座位存量控制的研究[D]. 成都: 西南交通大学, 2016. FANG Lei. Research on high-speed rail fare and seat inventory control based on revenue management[D]. Chengdu: Southwest Jiaotong University, 2016.

Dynamic pricing method for high-speed railway based on revenue management

XU Yan

(Passenger Transport Department of China Railway, Beijing 100844, China)

Based on the market pricing of high-speed railway, this paper proposed a dynamic pricing model of high-speed railway. Firstly, according to the train operation diagram differences, the trains were categorized with travel time; by analyzing the historical passenger flow information at various intervals along the high-speed railway, the passengers were classified according to the price sensitivity and time sensitivity, and the proportion of different types of passengers was calculated based on historical ticket sales data. Then, we established a generalized cost function for passenger travel. Combined with train classification, a dynamic pricing method for high-speed railway based on seat management was proposed, and then we established a passenger flow simulation model based on the principle of minimizing the general cost of passengers. Finally, the model used the Beijing-Shanghai high-speed railway as an example to simulate the passengers who have a fixed travel demand at various intervals along the Beijing-Shanghai high-speed railway. Through the ticketing process simulation, and assigning passengers to different optional trains, the income from the calculation model is increased compared with the original income, which means our study will provide a reference for dynamic pricing strategies for high-speed railways.

high-speed railway; revenue management; dynamic pricing; optimization model

10.19713/j.cnki.43−1423/u.2019.02.006

F532

A

1672 − 7029(2019)02 − 0319 − 07

2018−08−07

国家自然科学基金资助项目(U1334207)

徐彦(1973−)，女，湖北黄石人，高级工程师，从事铁路旅客运输研究；E−mail：enya.xuyan@foxmail.com

(编辑 蒋学东)