铁路桥梁弹塑性护栏设计及碰撞仿真研究
2019-03-07高广军陈功关维元吴永军
高广军,陈功,关维元,吴永军
铁路桥梁弹塑性护栏设计及碰撞仿真研究
高广军,陈功,关维元,吴永军
(中南大学 交通运输工程学院,轨道交通安全教育部重点实验室,湖南 长沙 410075)
提出一种适用于高速铁路桥梁弹塑性护栏设计,由立柱、吸能块和横梁组成。以3个组成部分的壁厚为设计变量,以吸能量和最大峰值力为目标响应,通过数值仿真得到优化拉丁超立方试验设计的样本空间。基于最小二乘法构建关于目标响应的三阶多项式响应面模型,通过多目标遗传算法对弹塑性护栏各组成部分的壁厚进行优化设计。以多目标优化设计的“平衡解”为弹塑性护栏的壁厚尺寸,建立简化的列车-弹塑性护栏-桥梁有限元模型,通过仿真对比现有防护墙和弹塑性护栏对脱轨列车的防护性能。研究结果表明:弹塑性护栏可以降低列车的撞击力,同时可以吸收部分碰撞能量。
铁路桥梁;弹塑性护栏;优化设计;碰撞仿真
为了保证高铁线路的平直,防止线路沉降,同时为了节约占地面积和不受地形条件的制约,高速铁路大多建在桥梁上。为了防止列车脱轨脱线后坠落桥底而发生对乘员安全以及财产损失的二次破坏,各国采取了相应的防护措施[1]。德国高速铁路采用无砟混凝土板式道床,桥面铺设标准设计的人行道遮板构件,以其电缆槽墙体作为防止列车脱轨的安全措施。瑞典高速铁路桥面采用加高的现浇挡碴墙来防止列车脱轨后冲出桥面。日本新干线桥面一般采用无砟混凝土板式道床,在明桥面上设有护轮轨。我国在高速铁路桥梁上主要采用防护墙来防止列车倾覆或冲出桥面,防护墙在铁路桥梁上的位置如图1所示。王川[2]对客货共线铁路桥梁列车脱轨后与防护墙碰撞过程进行分析,研究了防护墙的高度、考虑道床的下陷和防护墙墙体特征对于脱轨碰撞过程的影响规律。针对铁路桥梁的防护墙研究较少,但是对于国内外公路上的护栏有大量的研究。杜洋等[3]开展了半刚性护栏系统的冲击实验研究,结果表明波形梁的吸能量约为总吸收能量的50%~65%,防阻块的吸能量约为15%~25%,立柱的吸能量所占的比例很小。YIN等[4−5]基于径向基函数法对一种新型的η型护栏和一种混凝土护栏进行了优化设计。Wiebelhaus等[6−12]对混凝土护栏、波纹梁护栏和缆索护栏进行了全尺寸的实验研究。Elvik等[13]基于实际的统计数据研究了半刚性护栏等交通安全设施的有效性,然后提出了一些如何修改这些安全设施的建议。Borovinšk等[14]讨论了波纹梁护栏不同截面形状防阻块的吸能性能,发现六边形在能量吸收方面优势明显。现有的混凝土防护墙在防护过程中,几乎不能吸收列车的冲击动能,同时脱轨列车与混凝土防护墙之间的撞击力较大,对于整个桥梁强度要求较高。本文提出一种铁路桥梁段弹塑性护栏,通过响应面模型对弹塑性护栏结构的厚度尺寸进行了优化设计,然后基于CRTSI板式无砟轨道结构形式,建立简化的列车-弹塑性护栏−桥梁整体有限元模型,LS-DYNA仿真结果表明,设计的弹塑性护栏与原有的桥梁防护墙相比,排障器和后转向架区域的撞击力下降,可以对脱轨列车有更好的导向作用,同时弹塑性护栏可以吸收碰撞能量。
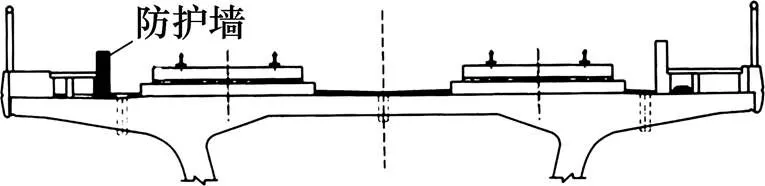
图1 铁路桥梁防护墙
1 高速铁路桥梁弹塑性护栏结构设计
本文提出一种适用于高速铁路桥梁段的弹塑性护栏设计,主要由立柱、吸能块和横梁组成。利用SolidWorks和HyperMesh软件建立弹塑性护栏的几何模型和有限元模型。图2所示为立柱模型,立柱的右半部分是一个半径为50 mm,高为1 000 mm的半圆柱,左半部分的上部是一个尺寸为100 mm ×50 mm×300 mm的方柱,下部是一个斜柱,其中最下端是一个边长为100 mm的矩形,整个立柱开有14个间隔为20 mm,尺寸为75 mm×20 mm的方孔,立柱厚度定义为。图3所示为吸能块模型,吸能块是一种吸能结构,高300 mm。其中一面是平面通过螺栓连接横梁,其他3面内凹,横向方向的凹面对应的圆心角为50°,通过螺栓与立柱连接,纵向方向2个凹面对应的圆心角均为60°,吸能块的厚度定义为。图4所示为横梁模型,横梁是一种双波梁的结构形式,高309 mm,波纹深度54 mm,厚度定义为。整个弹塑性护栏是一个薄壁结构,采用四节点的壳单元来模拟,网格大小为20 mm,同时利用MAT_PIECEWISE_LINEAR_ PLASTI- CITY材料定义弹塑性护栏材料属性。
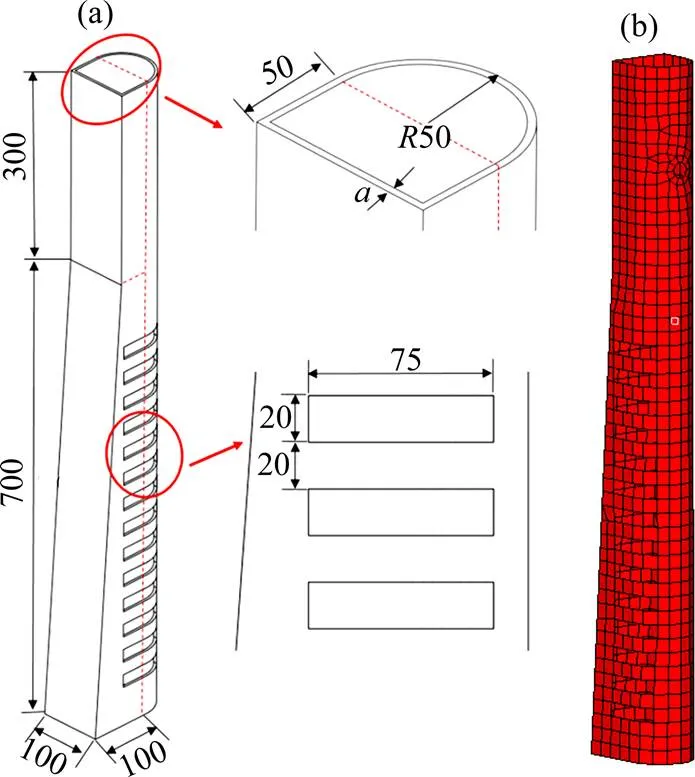
单位:mm
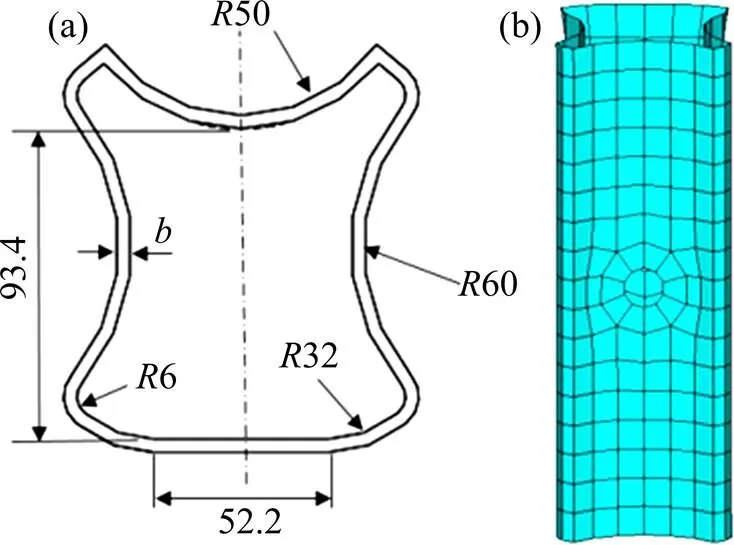
单位:mm
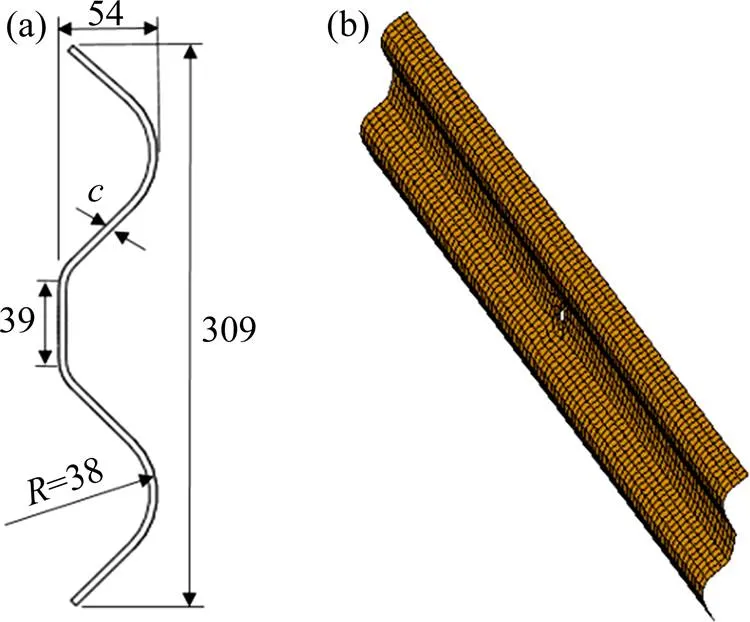
单位:mm
弹塑性护栏各组成部分的壁厚对于弹塑性护栏的整体吸能性能有较大的影响,因此需要得到一组合适的壁厚值,让弹塑性护栏的各组成部分都可以充分发挥吸能作用,同时也需要降低脱轨列车与弹塑性护栏之间的撞击作用力。进行优化设计时,由于立柱开口之后强度变低,立柱的壁厚应当大于吸能块的壁厚;横梁由于受到列车的直接冲击,因此横梁壁厚也大于吸能块的壁厚。综合考虑,立柱厚度和横梁厚度变化区间为5~12 mm,吸能块厚度变化区间为2.5~6 mm。
以,和为设计变量,通过优化拉丁超立方试验设计[15],得到所有样本点取值。采用LS- DYNA软件对弹塑性护栏进行碰撞仿真计算,选取质量为20 t的质量块,以18 m/s的初速度撞击立柱间隔为1 m,总跨度6 m的弹塑性护栏,有限元仿真模型如图5所示。横梁、吸能块和立柱之间通过刚性单元进行连接,给立柱底部所有节点施加固定约束。表1详细的列出了优化拉丁超方试验设计的样本点和计算得到的吸能量和最大峰值力。式(1)和式(2)分别为目标响应和与设计变量,和的3阶多项式响应面模型函数表达式。
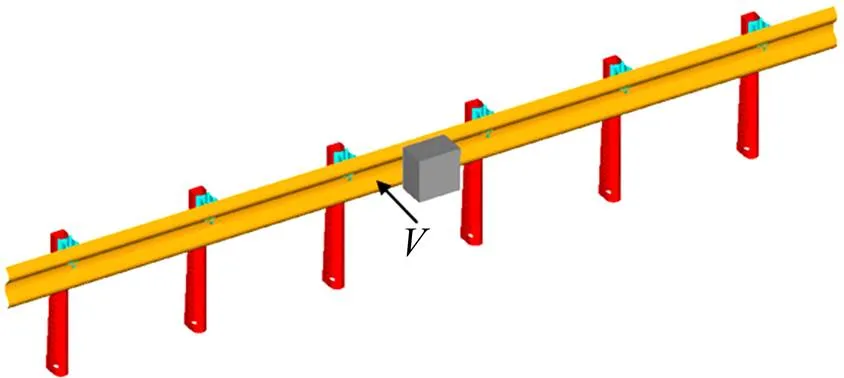
图5 有限元仿真模型
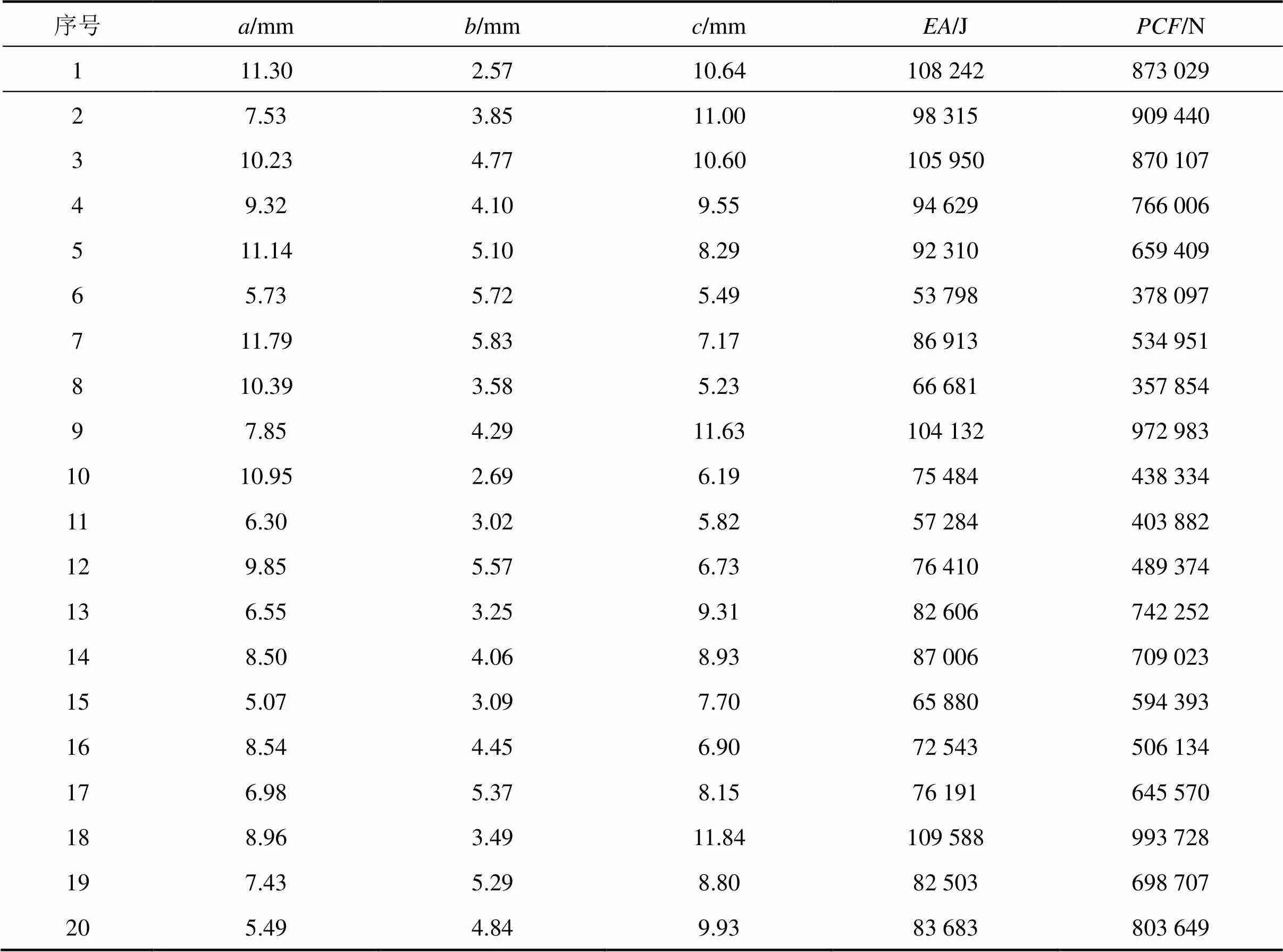
表1 样本点取值和仿真结果
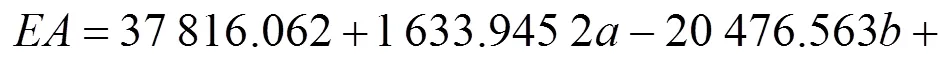
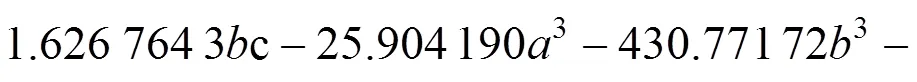
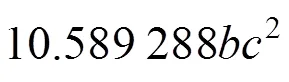
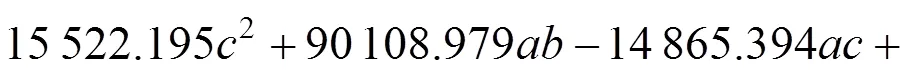
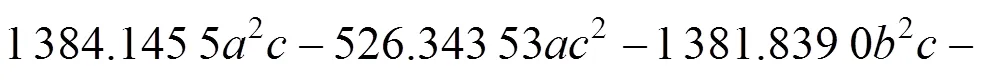
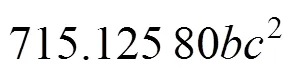
代理模型是通过响应近似值对实际响应值的逼近,响应值与真实值存在误差。本文通过决定系数R和平均相对误差来评估响应面模型的准确度,2个评价指标的表达式如下所示:
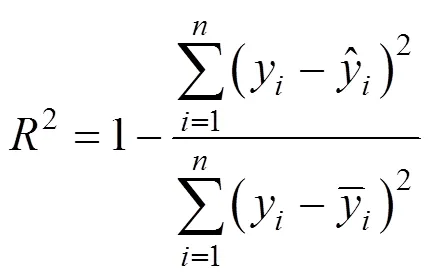
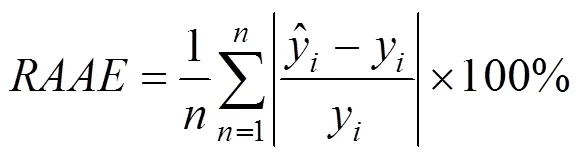
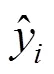

表2 响应面模型的精度
基于响应面模型,以最大的吸能量和最小的峰值力为优化目标,对弹塑性护栏结构的壁厚尺寸进行多目标优化设计。多目标优化的数学模型可以表示为式(5)。
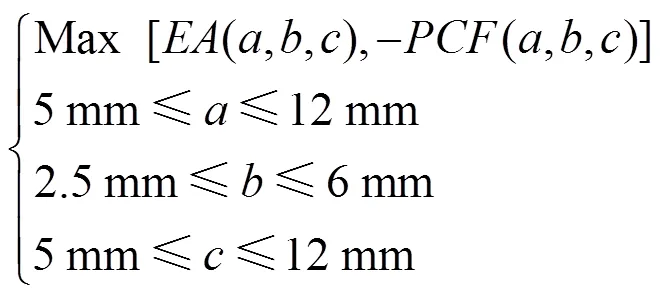
本文采用多目标遗传算法(MOGA)对壁厚的取值进行多目标优化,得到的Pareto前沿如图6所示,由图可知,3阶多项式响应面模型的目标响应吸能量和最大峰值力是正相关的。表3列出了不同约束条件下设计变量和目标响应的取值。点的约束条件是最大峰值力达到最小值,对应的设计变量=11.998 mm,=5.995 mm,=5.043 mm。点的约束条件吸能量达到最大值,对应的设计变量=11.995 mm,=5.855 mm,=11.992 mm。
为了在吸能量和最大峰值力之间做出一个合理的平衡,本文基于“距离最小化”标准得到了平衡它们之间相互矛盾的优化解点,“距离最小化”标准满足以下方程:
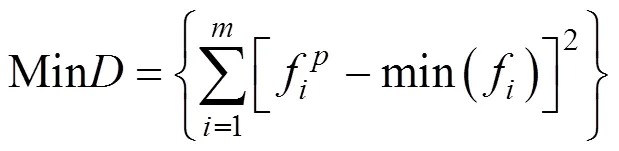
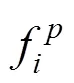
图6 弹塑性护栏的Pareto前沿
Fig. 6 Pareto frontier of the elastic-plastic guardrail

表3 不同约束条件下的弹塑性护栏优化方案
2 总体有限元仿真模型
图7(a)和7(b)是路基和列车有限元模型。选用曲线半径为2 200 m,外轨超高150 mm的高速铁路桥梁段,桥面结构采用的是简化的CRTSI板式无砟轨道,只考虑了路基在高度方向上的影响。路基转过的角度为3.334°,由于外轨超高引起5.707°的倾斜角。由于不考虑路基在碰撞过程中变形,因此路基设为刚体,相应的网格大小为50 mm。列车头车是大型的板、梁空间框架式结构,列车网格大小为50 mm,不考虑接触失效和悬挂装置的影响,转向架考虑为刚体,列车总重45 t。
图7(c)和7(d)是设计的弹塑性护栏和现有的防护墙有限元模型,距离轨道中心线1 900 mm,防护墙和弹塑性护栏长度取128 m。防护墙采用C50混凝土材料,在LS-DYNA中通过实体单元来模拟,并采用111号材料[2]。弹塑性护栏的材料为Q235,利用壳单元来模拟,壁厚采用上一节Pareto前沿中优化点B的取值。
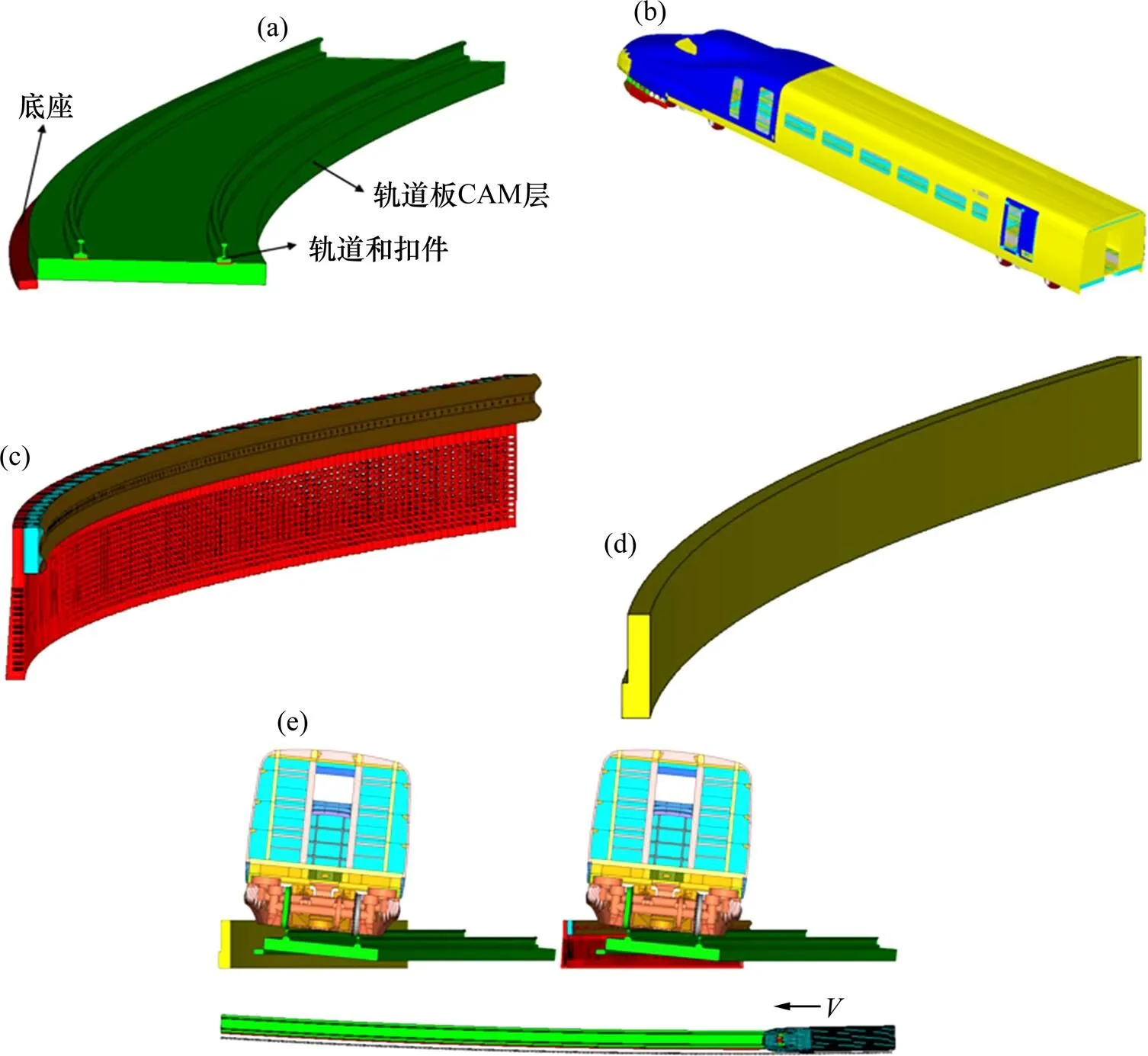
(a) 路基;(b) 列车;(c) 弹塑性护栏;(d) 防护墙;(e) 耦合系统
脱轨列车、防护设备和路基之间都设有自动面面接触,弹塑性护栏和脱轨列车本身设有自动单面接触。弹塑性护栏和防护墙的底部所有节点施加了固定约束,同时定义了脱轨列车沿轴正方向55.55 m/s的运行初速度。列车刚好脱离轨道设为计算的初始时刻[16],此时轮对横向偏移60 mm,垂向抬高27 mm。建立好的2种防护形式下的系统有限元模型如图7(e)所示。
3 仿真结果分析
整个撞击过程中,混凝土防护墙的吸能量为101 106 J,而弹塑性护栏各组成部分都吸收了冲击能量,其中立柱的吸能量为712 617 J,吸能块的吸能量为686 939 J,横梁的吸能量为430 218 J。弹塑性护栏的吸能量比混凝土防护墙的吸能量有了很大的提升。
如图8(a)所示是在现有防护墙防护形式下,排障器和防护墙的碰撞力−时间曲线。由于脱轨列车与防护设备之间存在一定的初始距离,列车前端的排障器在1.15 s开始与防护墙发生接触,各个方向的作用力迅速上升,横向方向和垂向方向的作用力都为正值,也就是说防护墙防止排障器继续朝轨道外侧偏移,同时防护墙对排障器有一个支持力的作用,方向的摩擦力为负值,与列车前进的方向相反。在1.46 s时,排障器受到的横向作用力达到最大值102.697 kN,而整个合力在1.41 s时达到最大值为159.124 kN。1.97 s时,列车驶出防护墙和轨道区域,排障器作用力降为0。如图8(b)所示是在弹塑性护栏防护形式下,排障器和弹塑性护栏的作用力−时间曲线,列车前端的排障器在1.10 s开始与弹塑性护栏发生接触。在1.51 s时,排障器受到的横向作用力达到最大值97.018 kN,而整个合力在1.55 s时达到最大值为130.083 kN。与现有防护墙相比,在弹塑性护栏防护作用下,列车排障器受到的横向作用力最大值下降了5.5%,而受到的总合力最大值下降了18.3%。
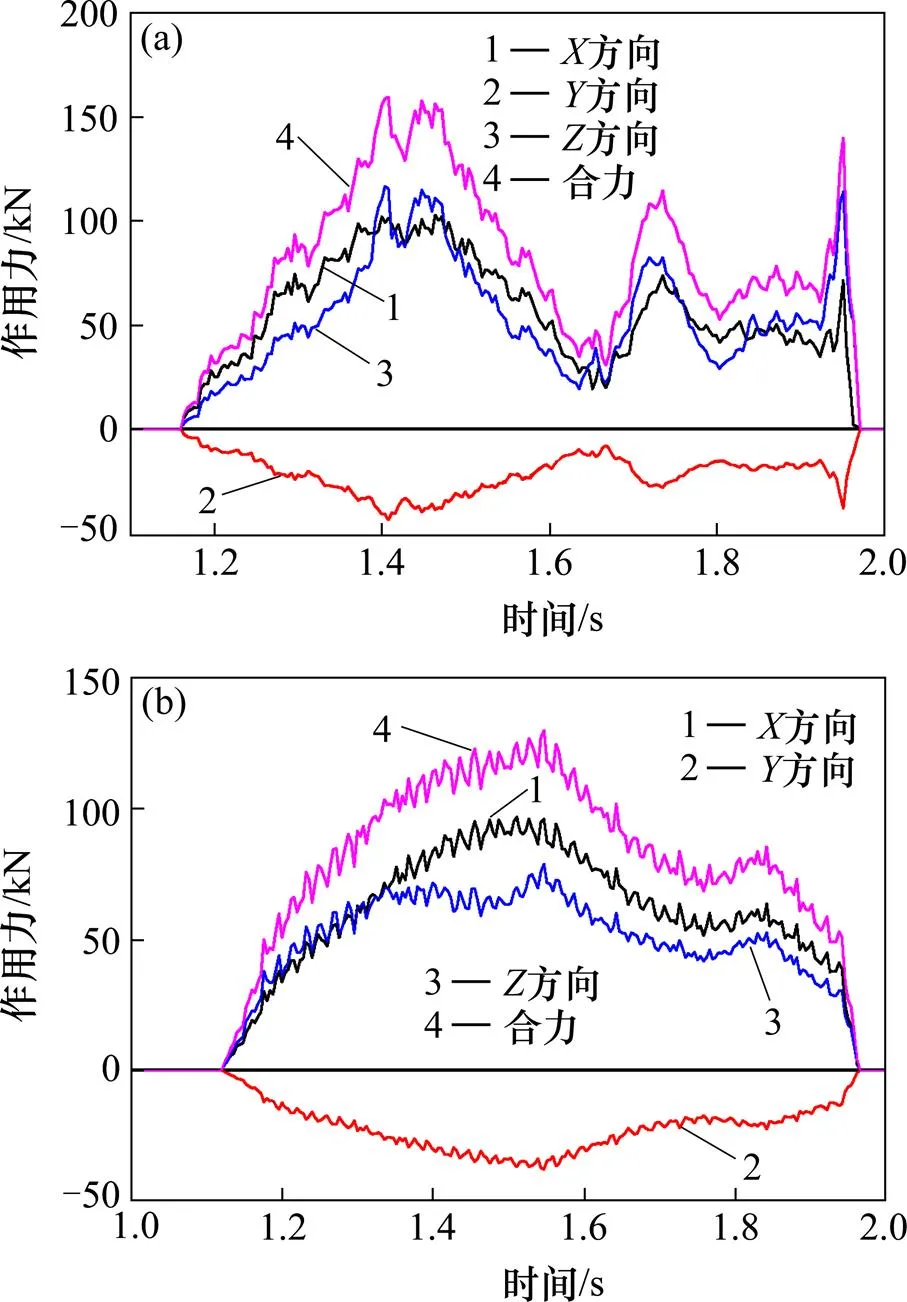
(a) 防护墙;(b) 弹塑性护栏
如图9(a)所示是后转向架与防护墙之间的作用力−时间曲线,列车后转向架在1.07 s开始接触防护墙,横向作用力在1.11 s达到最大值466.224 kN,合力在1.12 s达到最大值952.842 kN。如图9(b)所示是后转向架与弹塑性护栏之间的作用力−时间曲线,列车后转向架在0.99 s开始接触弹塑性护栏,横向作用力在1.30 s达到最大值144.989 kN,合力在1.18 s达到最大值427.141 kN。与现有防护墙相比,在弹塑性护栏防护作用下,列车后转向架受到的横向作用力最大值下降了68.9%,而受到的总合力最大值下降了55.2%,下降幅度非常明显。
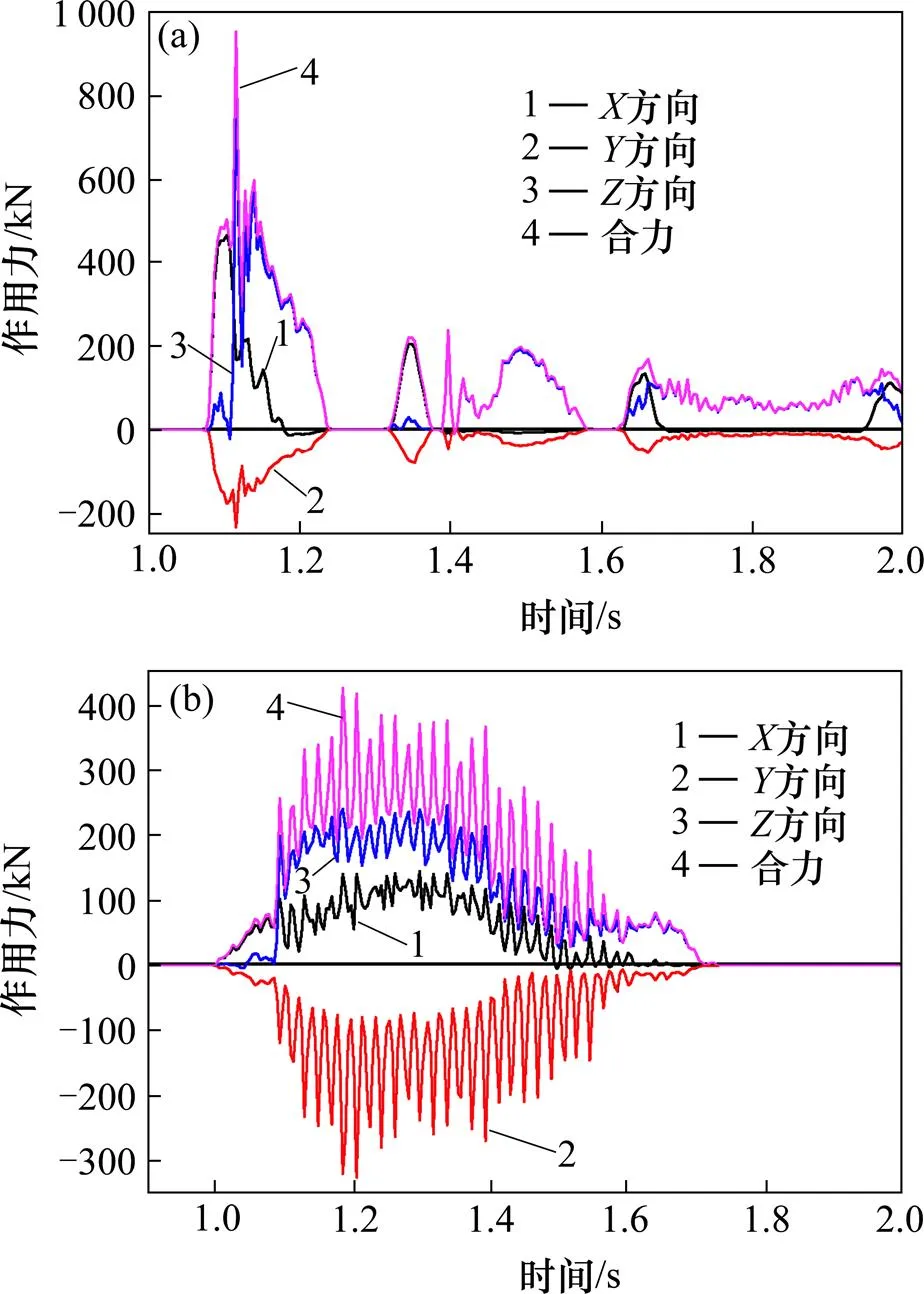
(a) 防护墙;(b) 弹塑性护栏
为了更好地掌握防护墙和弹塑性护栏对脱轨列车的导向和保护作用,在列车前后转向架内侧空气弹簧处分别设置了前后测点。如图10所示是前后测点横向位移−时间曲线,1.252 s时,在防护墙防护作用下,前测点横向位移是1231.22 mm,后测点横向位移是328.19 mm,前后测点的位移差为903.03 mm。而在弹塑性护栏防护作用下,前测点横向位移是1 250.81 mm,后测点横向位移是287.17 mm,前后测点的位移差为963.64 mm。1.752 s时,在防护墙防护作用下,前测点横向位移是2 361.63 mm,后测点横向位移是1 341.84 mm,前后测点的位移差为1 019.79 mm,而在弹塑性护栏防护作用下,前测点横向位移是2 411.30 mm,后测点横向位移是1 546.35 mm,前后测点的位移差为864.95 mm。前后测点的位移差变小,说明弹塑性护栏对脱轨列车的导向作用更好。
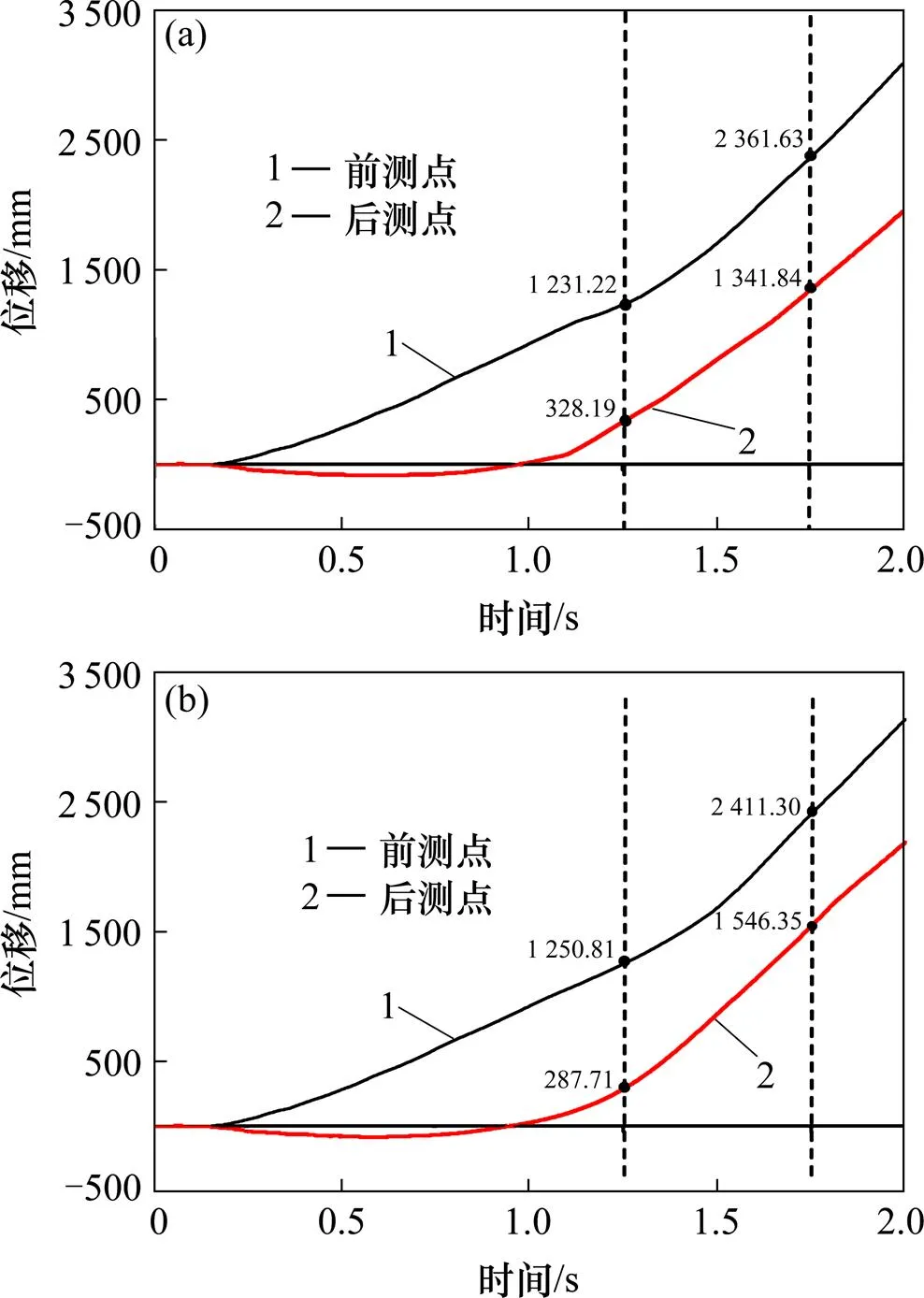
(a) 防护墙;(b) 弹塑性护栏
4 结论
1) 提出一种适用于高速铁路桥梁弹塑性护栏设计,该护栏由立柱、吸能块和横梁组成。以3个组成部分的壁厚为设计变量,通过数值仿真得到优化拉丁超立方试验设计样本点的响应值(吸能量和最大峰值力),基于最小二乘法构建关于目标响应的3阶多项式响应面模型,通过多目标遗传算法对弹塑性护栏的壁厚进行多目标优化设计得到Pareto前沿。
2) 以多目标优化设计的“平衡解”(=10.120 mm,=2.500 mm,=10.800 mm)为弹塑性护栏的壁厚尺寸,建立列车−弹塑性护栏−桥梁的有限元模型,通过仿真对比了现有防护墙和设计的弹塑性护栏对脱轨列车的防护性能,结果表明,弹塑性护栏可以大幅降低列车的撞击力,其中对排障器的作用力降低了18.3%,对后转向架的作用力降低了55.2%。
3) 相比现有的防护墙,本文提出的弹塑性护栏对脱轨列车有良好的导向作用,同时可以吸收更多的碰撞能量。
[1] 肖沁凯. 高速铁路桥梁安全防护措施分析[J]. 铁道标准设计, 2010(6): 70−72. XIAO Qinkai. Analysis of safety protection measures for high speed railway bridge[J]. Railway Standard Design, 2010(6): 70−72.
[2] 王川. 客货共线铁路桥梁列车脱轨后与防护墙碰撞过程研究[D]. 长沙: 中南大学, 2014. WANG Chuan. Research on the process of collision between derailed trains and protective walls on mixed passenger and freight railway bridges[D]. Changsha: Central South University, 2014.
[3] 杜洋, 黄小清, 汤立群. 半刚性护栏系统模型冲击实验研究[J]. 华南理工大学学报(自然科学版), 2003, 31(12): 66−70.DU Yang, HUANG Xiaoqing, TANG Liqun. Impact experiment of semi-rigid guardrail system model[J]. Journal of South China University of Technology, 2003, 31(12): 66−70.
[4] YIN Hanfeng, XIAO Youye, WEN Guilin, et al. Design optimization of a new W-beam guardrail for enhanced highway safety performance[J]. Advances in Engineering Software, 2017, 112: 154−164.
[5] YIN Hanfeng, FANG Hongbing, WANG Qian, et al. Design optimization of a MASH TL-3 concrete barrier using RBF-based metamodels and nonlinear finite element simulations[J]. Engineering Structures, 2016, 114: 122−134.
[6] Wiebelhaus M J, Lechtenberg K A, Faller R K, et al. Development of a temporary concrete barrier to permanent concrete median barrier approach transition[R]. Impact Tests, 2010.
[7] Rosenbaugh S K, Faller R K, Bielenberg B W, et al. Development of the MGS approach guardrail transition using standardized steel posts[J]. Highway Safety, 2010.
[8] Wiebelhaus M J, Sicking D L, Faller R K, et al. Phase I: Development of a non-proprietary, four-cable, high tension median barrier[R]. Highway Safety, 2011.
[9] Schmidt J, Sicking D L, Faller R K, et al. Phase II: Development of a non-proprietary, four-cable, high tension median barrier[R]. Highway Safety, 2012.
[10] Stolle C J, Lechtenberg K A, Faller R K, et al. Determination of the maximum mgs mounting height-- Phase I crash testing[R]. Guardrails, 2012.
[11] Julin R D, Faller R K, John R, et al. Determination of the maximum MGS mounting height Phase II detailed analysis[R]. Height, 2012.
[12] Lechtenberg K A, Bielenbery R W, Faller R K, et al. Midwest guardrail system with southern yellow pine posts[R]. Impact Tests, 2013.
[13] Elvik R, Christensen P, Amundsen A. Speed and road accidents: An evaluation of the power model[R]. Nordic Road & Transport Research, 2004.
[14] Borovinšk M, Vesenjak M, Ulbin M, et al. Simulation of crash tests for high containment levels of road safety barriers[J]. Engineering Failure Analysis, 2007, 14(8): 1711−1718.
[15] XU Ping, YANG Chengxing, PENG Yong, et al. Crash performance and multi-objective optimization of a gradual energy-absorbing structure for subway vehicles [J]. International Journal of Mechanical Sciences, 2016, 107: 1−12.
[16] 翟婉明, 陈果. 根据车轮抬升量评判车辆脱轨的方法与准则[J]. 铁道学报, 2001, 23(2): 17−26. ZHAI Wanming, CHEN Guo. Method and criteria for evaluation of wheel derailment based on wheel vertical rise[J]. Journal of the China Railway Society, 2001, 23(2): 17−26.
Design of elastic-plastic guardrail on the railway bridge and its crash simulation study
GAO Guangjun, CHEN Gong, GUAN Weiyuan, WU Yongjun
(Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)
A kind of elastic-plastic guardrail for the high-speed railway bridge is proposed in this paper, which is composed of column, energy absorption block and beam. The wall thicknesses of the three parts were used as the design variables, the(absorbing energy) and the(maximum peak force) as the target response. The optimal Latin hypercube test design, combined with the finite element simulation to get the sample space. Three order polynomial response surface models for target responses were established based on least square method. The multi-objective genetic algorithm was used to optimize the wall thickness of the elastic-plastic guardrail. The “equilibrium solution” of the multi-objective optimization design were set as the wall thickness of the elastic- plastic guardrail, and a simplified train-elastic-plastic guardrail-bridge finite element model was established. The protection performance of the existing protective wall and elastic-plastic guardrail on the derailment train were compared through simulation. The results show that the elastic-plastic guardrail can greatly reduce the impact force of the train and can absorb some collision energy at the same time.
railway bridge; elastic-plastic guardrail; optimal design; crash simulation
10.19713/j.cnki.43−1423/u.2019.02.015
U260
A
1672 − 7029(2019)02 − 0391 − 08
2018−02−01
国家重点研发计划资助项目(2016YFB1200403);国家自然科学基金资助项目(U1334208);中南大学理工医学科第二批战略先导立项专项项目(ZLXD2017002);中国铁路总公司重点科研项目(2016J009-F)
高广军(1973−),男,河南安阳人,教授,从事列车撞击动力学研究;E−mail:gjgao@csu.edu.cn
(编辑 涂鹏)
